故障树
时间20210105
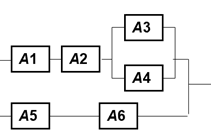
可以根据这道题目学习故障树。假设系统的可靠性逻辑框图如下所示。
故障树的定义
用以表明产品哪些组成部分的故障或外界事件或它们的组合将导致产品发生一种给定故障的逻辑图。
故障树是一种逻辑因果关系图,构图的元素是事件和逻辑门:事件用来描述系统和元部件故障的状态;逻辑门把事件联系起来,表示事件之间的逻辑关系。
故障树分析(FTA):通过对可能造成产品故障的硬件、软件、环境、人为因素进行分析,画出故障树,从而确定产品故障原因的各种可能组合方式和(或)其发生概率。
建立故障树的目的
- 帮助判明可能发生的故障模式和原因;
- 发现可靠性和安全性薄弱环节,采取改进措施,以提高产品可靠性和安全性;
- 计算故障发生概率;
- 发生重大故障或事故后,FTA是故障调查的一种有效手段,可以系统而全面地分析事故原因,为故障“归零”提供支持;
- 指导故障诊断、改进使用和维修方案等。
故障树特点
- 是一种自上而下的图形演绎方法;
- 有很大的灵活性;
- 综合性:硬件、软件、环境、人为因素等;
- 主要用于安全性分析。
故障树的画法
故障树常用事件符号
故障树常用逻辑门符号
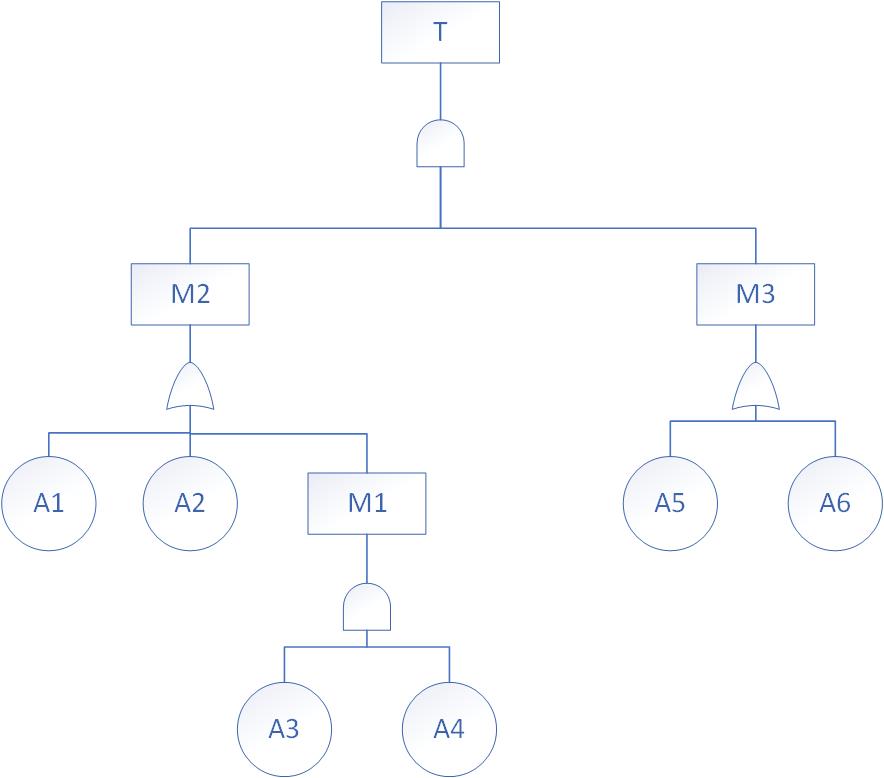
上述题目的故障树图可以画出如下。
割集和路集
割集:故障树中一些底事件的集合,当这些底事件同时发生时,顶事件必然发生;
最小割集:若将割集中所含的底事件任意去掉一个就不再成为割集了,这样的割集就是最小割集。
路集:故障树中一些底事件的集合,当这些底事件同时不发生时,顶事件必然不发生;
最小路集:若将路集中所含的底事件任意去掉一个就不再成为路集了,这样的路集就是最小路集。
上述题目的最小割集表达式:
T
=
M
2
⋅
M
3
=
(
A
1
+
A
2
+
M
1
)
⋅
(
A
5
+
A
6
)
=
(
A
1
+
A
2
+
A
3
⋅
A
4
)
⋅
(
A
5
+
A
6
)
=
A
1
A
5
+
A
1
A
6
+
A
2
A
5
+
A
2
A
6
+
A
3
A
4
A
5
+
A
3
A
4
A
6
T = M_2·M3 \\ = (A1+A2+M1)·(A5+A6) \\ = (A1+A2+A3·A4)·(A5+A6) \\ = A1A5+A1A6+A2A5+A2A6+A3A4A5+A3A4A6
T=M2⋅M3=(A1+A2+M1)⋅(A5+A6)=(A1+A2+A3⋅A4)⋅(A5+A6)=A1A5+A1A6+A2A5+A2A6+A3A4A5+A3A4A6
底事件的结构重要度
一棵故障树模型中往往包含多个底事件,各个底事件在故障树中的重要性必然因它们所代表的设备在系统中的位置(或作用,功能)的不同而不同。因此,对底事件的发生在顶事件的发生中所作的贡献可称作底事件的重要度。
故障树的事件结构重要度:重要度是基本事件或割集对系统故障树顶事件发生的贡献,是一种灵敏度分析。结构重要度分析,是从故障树结构上分析各基本事件对顶事件发生的贡献,即在不考虑基本事件发生概率,或者设基本事件发生概率相等的情况下,分析各基本事件的发生对顶事件发生的贡献。贡献的大小用数值表示,成为基本事件结构重要度。结构重要度分析就是要求出各基本事件的结构重要度及排出机构重要度顺序。
设故障树有n各基本事件,每个基本事件都有发生(记为 X i = 1 X_i=1 Xi=1)和不发生(记为 X i = 0 X_i=0 Xi=0)两种状态。现假定基本事件 X i X_i Xi的状态由0变为1,其它基本事件的状态不变,对于单调系统顶事件的状态变化可能由三种情况。
- θ ( 0 i , X ) = 0 → θ ( 1 i , X ) = 0 \theta(0_i,X)=0 \rightarrow \theta(1_i,X)=0 θ(0i,X)=0→θ(1i,X)=0
- θ ( 0 i , X ) = 0 → θ ( 1 i , X ) = 1 \theta(0_i,X)=0 \rightarrow \theta(1_i,X)=1 θ(0i,X)=0→θ(1i,X)=1
- θ ( 0 i , X ) = 1 → θ ( 1 i , X ) = 1 \theta(0_i,X)=1 \rightarrow \theta(1_i,X)=1 θ(0i,X)=1→θ(1i,X)=1
注意这里是没有1到0的,因为一个部件故障,一般不会从故障变为正常。
这里只有第二种情况对顶事件发生有贡献。对一个具有n个基本事件的故障树,它的结构函数 θ ( X ) \theta(X) θ(X)是一个具有n个变元的布尔函数式,它的定义域为 2 n 2^n 2n个n元值组。将变元 X i X_i Xi由0变为1所引起的 2 n 2^n 2n个n元值组中由 θ ( 0 i , X ) = 0 \theta(0_i,X)=0 θ(0i,X)=0变为 θ ( 1 i , X ) = 1 \theta(1_i,X)=1 θ(1i,X)=1(使顶事件由0变为1)的状态数累加起来,乘上一个权重系统 1 / 2 n − 1 1/2^{n-1} 1/2n−1,就称为 X i X_i Xi的结构重要度,用 I θ ( i ) I_\theta(i) Iθ(i)表示
I θ = 1 2 n − 1 ∑ [ θ ( 1 i , X ) − θ ( 0 i , X ) ] I_\theta=\frac {1}{2^{n-1}} \sum[\theta(1_i,X)-\theta(0_i,X)] Iθ=2n−11∑[θ(1i,X)−θ(0i,X)]
补充些知识便于理解上述的三个方面,一般只研究两状态故障树,即系统和部件只能取正常或故障两种状态,故可用0,1。Xi变量来描述底事件的状态,于是有
X i = { 1 , 当 底 事 件 i 发 生 时 ; 0 , 当 底 事 件 i 不 发 生 时 。 X_i=\left \{ \begin{array}{c} 1,当底事件i发生时; \\ 0,当底事件i不发生时。 \end{array} \right. Xi={1,当底事件i发生时;0,当底事件i不发生时。
由于顶事件的状态是底事件状态的函数,如用
θ
(
X
)
=
θ
(
X
1
,
X
2
,
.
.
.
.
.
.
,
X
r
)
\theta(X)=\theta(X_1,X_2,......,X_r)
θ(X)=θ(X1,X2,......,Xr)描述顶事件的状态,这里r表示的是r个部件。
θ ( X ) = { 1 , 当 顶 事 件 T 发 生 时 ; 0 , 当 顶 事 件 T 不 发 生 时 。 \theta(X)=\left \{ \begin{array}{c} 1,当顶事件T发生时;\\ 0,当顶事件T不发生时。 \end{array} \right. θ(X)={1,当顶事件T发生时;0,当顶事件T不发生时。
网址:基于故障树的数控机床故障诊断系统的研究 (1) - 豆丁网
对于上述题目,可以使用
对于某种特殊情况下,
p
1
=
p
2
=
p
3
=
p
4
=
p
5
=
p
6
=
1
/
2
p1=p2=p3=p4=p5=p6=1/2
p1=p2=p3=p4=p5=p6=1/2
I
1
=
I
2
=
P
{
T
=
1
∣
A
1
=
1
}
−
P
{
T
=
1
∣
A
1
=
0
}
=
(
p
5
+
p
6
−
p
5
p
6
)
−
(
p
2
+
p
3
p
4
−
p
2
p
3
p
4
)
(
p
5
+
p
6
−
p
5
p
6
)
=
3
/
4
−
3
/
4
∗
5
/
8
=
9
/
32
I_1=I_2=P\{T=1|A_1=1\}-P\{T=1|A_1=0\}\\ =(p_5+p_6-p_5p_6)-(p_2+p_3p_4-p_2p_3p_4)(p_5+p_6-p_5p_6)\\ =3/4-3/4*5/8\\ =9/32
I1=I2=P{T=1∣A1=1}−P{T=1∣A1=0}=(p5+p6−p5p6)−(p2+p3p4−p2p3p4)(p5+p6−p5p6)=3/4−3/4∗5/8=9/32
同理可以解的,
I
3
=
I
4
=
3
/
32
I_3=I_4=3/32
I3=I4=3/32,
I
5
=
I
6
=
13
/
32
I_5=I_6=13/32
I5=I6=13/32
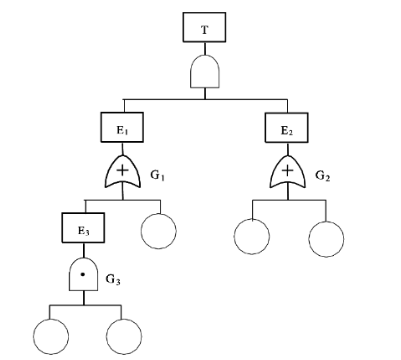
通过可靠性逻辑框图画出故障树
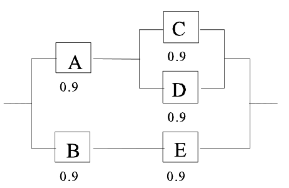
一个系统由5个单元组成,可靠性逻辑框图如下,求该系统可靠度和画出故障树,并求出故障树的最小割集和最小路集。
解:最小路集:AC,AD,BE;最小割集:AB,CDE,AE,BCD。
R = 1-(1-0.9*0.9)(1-0.9[1-0.1*0.1]) = 0.8929
理解:从左到右应该是表示:C,D,A,B,E发生故障。然后按照一般的理解就可以了。