从一个2维的样本集开始,该实现可以帮助读者对k-means算法有一个直观的感受。
然后将使用k-means算法对图像进行压缩,通过减少颜色数量,直到只出现在该图像中最常见的那些颜色。
1 数据文件
数据集ex7data2.mat:二维样本集
需要压缩的图片文件bord_small.png。
2 Python 关键语法理解
2.1 np.argmin函数返回最小值的索引。
2.2 np.linalg.norm()用于求范数。
linalg本意为linear(线性) + algebra(代数),norm则表示范数。
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
x: 表示矩阵(一维数据也是可以)
ord: 表示范数类型
| 参数 | 说明 | 计算方法 |
| 默认 | 二范数: | |
| ord =2 | 二范数: | 同上 |
| ord =1 | 一范数: | |
| ord =np.inf | 无穷范数: | |
2.3 matplotlib.image程序包中image.imread函数,读取图片,imsave函数,保存图片。
3 完整代码
#####################################################
## Part 1 为k-means聚类,首先从一个2维的样本集开始,
# 可以帮助你对k-means算法有一个直观的感受。
#####################################################
print('\n第一部分 直观感受k-means........\n')
# 第一步 导入数据及可视化
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
fileName = 'ex7data2.mat'
data = sio.loadmat('ex7data2.mat')
print(f'\n数据集{fileName}中的键名 data.keys() = {data.keys()}')
X = data['X']
print(f'\n数据集{fileName}中的样本 X.shape = {X.shape}')
def plot_data(x):
plt.scatter(X[:,0],X[:,1],label = 'train',marker='o', c='y', edgecolors='g')
plt.show
plot_data(X)
# 第二步 簇分配,
# 2.1 定义簇分配函数
def find_centroids(X,centros):
idx = []
for i in range(len(X)):
#X[i](2,)centros(k,2)=>(k,2)
#计算距离
dist = np.linalg.norm((X[i]-centros),axis = 1)#(k,)
id_i = np.argmin(dist)
idx.append(id_i)
return np.array(idx)
# 2.2 初始聚类中心
centros = np.array([[3,3],[6,2],[8,5]])
idx = find_centroids(X,centros)
idx[:3]
# 第三步 计算聚类中心,
# 3.1 定义计算聚类中心函数
def compute_centros(X,idx,k):
centros = []
for i in range(k):
centros_ = np.mean(X[idx == i],axis = 0)
centros.append(centros_)
return centros
print(f'计算聚类中心的结果 = {compute_centros(X,idx,k = 3)}')
# 第四步 执行kmeans过程
# 4.1 定义执行k—means过程函数
def run_kmeans(X,centros,iters):
k = len(centros)
centros_all = []
centros_all.append(centros)
centros_i = centros
for i in range(iters):
idx = find_centroids(X,centros_i)
centros_i = compute_centros(X,idx,k)
centros_all.append(centros_i)
return idx,np.array(centros_all)
# 4.2 执行 执行kmeans过程
print(f'样本 X.sahpe = {X.shape}, 聚类中心 centros.shape = {centros.shape}')
idx,centros_all = run_kmeans(X,centros,iters = 100)
# 第五步 绘制kmeans过程
# 5.1 定义绘制数据集和聚类中心的移动轨迹函数
def plot_data1(X,centros_all,idx):
plt.figure()
plt.scatter(X[:,0],X[:,1],c= idx,cmap = 'rainbow')#数据集颜色根据x类别来区分
plt.plot(centros_all[:,:,0],centros_all[:,:,1],'kx--')
return
# 5.2 绘制聚类中心的移动轨迹
plot_data1(X,centros_all,idx)
#####################################################
## Part 2 使用k-means算法对图像进行压缩,通过减少颜色数量,
# 直到只出现在该图像中最常见的那些颜色。
# 案例: 使用kmeans对图片颜色进行聚类
# RGB图像,每个像素点值范围0-255
#####################################################
print('\n第二部分 使用k-means算法对图像进行压缩,通过减少颜色数量........\n')
# 第一步 导入图像 读入图像文件bird small.png,
# 得到一个三维矩阵A,它的前两个值表示像素位置,最后一个值表示红色、绿色或蓝色。
# 比如, A(50,33,3)表示坐标为(50,33 )的像素点的蓝色强度值,
# A(50,33,1)表示坐标为(50,33)的像素点的红色强度值(
# 这里下标从 1 1 1开始,代码中下标从 0 0 0开始,注意区分)。
# 接下来,利用该矩阵,创建像素颜色矩阵 m×3 (m=16384=128×128),
# 并调用K-means相关函数。
from skimage import io
fileName = 'bird_small.png'
A = io.imread(fileName)
A = A/255 #RGB的三个值[0,255],将它们范围设置为[0,1]
print(f'\n图片{fileName}的 shape = {A.shape}')
# 第二步 压缩图片
# 原始图像对128×128个像素点中的每一个的RGB颜色描述需要24位:
# (3×8=24,2^8=256,而RGB的范围为[0,255])
# 总大小为 128×128×24=393216位
# 为了对图片进行压缩,接下来找到最合适的 16 种颜色来表示图像,
# 调用函数findClosestCentroids为每一个像素点寻找最近的簇心。
# 而现在只需要16种颜色,每一种需要 24位,来表示图像,
# 图像本身每个像素点需要4位来表示选择了哪种颜色(2^4=16)
# 总大小为16×24+128×128×4=65920
# 这样就通过减少颜色数量实现了图像压缩
# 2.1 定义初始化聚类中心函数
def kMeansInitCentroids(x, K):
randidx = np.random.permutation(x) #随机排列
centroids = randidx[:K, :] #选前K个
return centroids
#方法二
# def inti_centroids(X,k):
# index = np.random.choice(len(X),k)
# return X[index]
# 2.2 初始化聚类中心
K = 16 #16种颜色
X = A.reshape(-1,3) #创建像素颜色矩阵m*3,reshape(-1, 3)表示行数由Numpy自动计算,3列
centroids = kMeansInitCentroids(X, K) #随机初始化得到K个簇心
print(f'\n{K}个聚类中心的形状 centroids.shape ={centroids.shape}')
# 2.3 通过运行K-means,找到最优的16种颜色来压缩图片
idx,centroids_all = run_kmeans(X, centroids,10) # 运行K-means centroids_all:(11*16)
centros = centroids_all[-1] # 取迭代完的最后一个,即找到最优化的16种颜色
print(f'\n原图像素点的形状:idx.shape ={idx.shape}')
print(f'\n压缩后各像素点上对应{K}颜色中的索引值 idx ={idx}')
print(f'\n最优化的{K}种颜色的 shape ={centros.shape}')
print(f'\n最优化的{K}种颜色 ={centros}')
# 2.4 将最优的颜色赋给压缩后的图像
img = np.zeros(X.shape) # 初始化压缩后图像的颜色为黑色0
for i in range(len(centros)):
img[idx==i]=centros[i]
# 或用以下代码
'''
for i in range(len(img)):
temp = idx[i] # 取出该像素点上对应的16种图像的索引值
img[i] = centros[temp] # 将16种图像中与索引值对应的颜色值赋给像素点
'''
# 2.5 将压缩图像的形状还原为能显示的形状
img = img.reshape(128,128,3)
# 2.6 与原图并列显示压缩后的图像
plt.figure(1,figsize=(12.8,4.8))
plt.subplot(1,2,1)
plt.imshow(A)
plt.subplot(1,2,2)
plt.imshow(img)
plt.show()
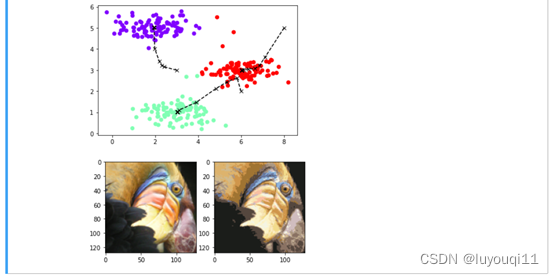
执行结果如下: