「力扣」题解链接:回溯算法(画图分析剪枝条件)。
题目描述:
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
示例:
输入: "25525511135"
输出: ["255.255.11.135", "255.255.111.35"]
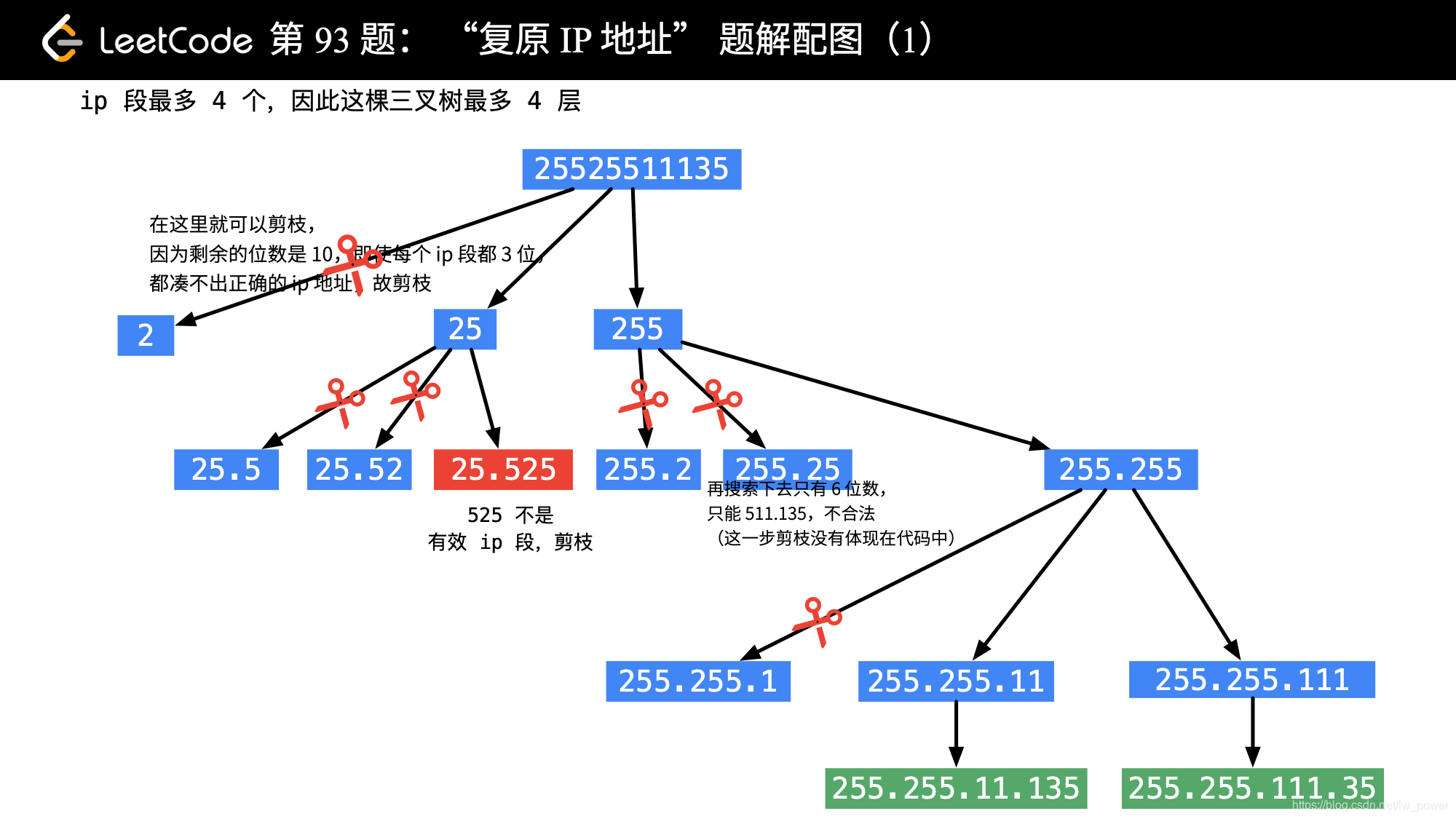
思路分析:回溯算法事实上就是在一个树形问题上做深度优先遍历,因此首先需要把问题转换为树形问题。这里请大家一定要拿起纸和笔,模拟一下如何通过指定的字符串 s 生成 IP 地址的过程,把树形图画出来(这一点很重要)。
下面这张图我没有画完(如果画完,枝叶太多),请读者尽量不看我画的这张图,自己动手尝试一下这个问题的树形图应该怎么画。
在画树形图的过程中,你一定会发现有些枝叶是没有必要的,把没有必要的枝叶剪去的操作就是剪枝,在代码中一般通过 break 或者 contine 和 return (表示递归终止)实现。
分析剪枝条件(下面只写出一些我想到的要点,有些点能想到,但是编码很复杂,我就没有写了):
1、一开始,字符串的长度小于 4 或者大于 12 ,一定不能拼凑出合法的 ip 地址(这一点可以一般化到中间结点的判断中,以产生剪枝行为);
2、每一个结点可以选择截取的方法只有 3 种:截 1 位、截 2 位、截 3 位,因此每一个结点可以生长出的分支最多只有 3 条分支;
根据截取出来的字符串判断是否是合理的 ip 段,这里写法比较多,可以先截取,再转换成 int ,再判断。我采用的做法是先转成 int,是合法的 ip 段数值以后,再截取。
3、由于 ip 段最多就 4 个段,因此这棵三叉树最多 4 层,这个条件作为递归终止条件之一;
4、每一个结点表示了求解这个问题的不同阶段,需要的状态变量有:
splitTimes:已经分割出多少个 ip 段;begin:截取 ip 段的起始位置;path:记录从根结点到叶子结点的一个路径(回溯算法常规变量,是一个栈);res:记录结果集的变量,常规变量。
总结:这个问题思想不难,但是细节比较繁琐,什么时候递归终止,如何手动截取字符串,再转换成 int 类型,还有如何在中间结点发现可以剪枝,这些细节需要在编码的时候考虑清楚。
有一些编码细节写在代码注释中,供大家参考,可能还有漏掉的地方,欢迎大家给出意见。我给出的代码执行时间也不是很好。
参考代码 1: 这一版代码比较慢,原因有可能是剪枝判断太多了,也有可能是 ipSegment + "" 这个操作耗时。
Java 代码:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
import java.util.Stack;
public class Solution {
public List<String> restoreIpAddresses(String s) {
int len = s.length();
List<String> res = new ArrayList<>();
// 如果长度不够,不搜索
if (len < 4 || len > 12) {
return res;
}
Deque<String> path = new ArrayDeque<>(4);
int splitTimes = 0;
dfs(s, len, splitTimes, 0, path, res);
return res;
}
/**
* 判断 s 的子区间 [left, right] 是否能够成为一个 ip 段
* 判断的同时顺便把类型转了
*
* @param s
* @param left
* @param right
* @return
*/
private int judgeIfIpSegment(String s, int left, int right) {
int len = right - left + 1;
// 大于 1 位的时候,不能以 0 开头
if (len > 1 && s.charAt(left) == '0') {
return -1;
}
// 转成 int 类型
int res = 0;
for (int i = left; i <= right; i++) {
res = res * 10 + s.charAt(i) - '0';
}
if (res > 255) {
return -1;
}
return res;
}
private void dfs(String s, int len, int split, int begin, Deque<String> path, List<String> res) {
if (begin == len) {
if (split == 4) {
res.add(String.join(".", path));
}
return;
}
// 看到剩下的不够了,就退出(剪枝),len - begin 表示剩余的还未分割的字符串的位数
if (len - begin < (4 - split) || len - begin > 3 * (4 - split)) {
return;
}
for (int i = 0; i < 3; i++) {
if (begin + i >= len) {
break;
}
int ipSegment = judgeIfIpSegment(s, begin, begin + i);
if (ipSegment != -1) {
// 在判断是 ip 段的情况下,才去做截取
path.addLast(ipSegment + "");
dfs(s, len, split + 1, begin + i + 1, path, res);
path.removeLast();
}
}
}
}
Python 代码:
from typing import List
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
size = len(s)
if size < 4 or size > 12:
return []
path = []
res = []
self.__dfs(s, size, 0, 0, path, res)
return res
def __dfs(self, s, size, split_times, begin, path, res):
if begin == size:
if split_times == 4:
res.append('.'.join(path))
return
if size - begin < (4 - split_times) or size - begin > 3 * (4 - split_times):
return
for i in range(3):
if begin + i >= size:
break
ip_segment = self.__judge_if_ip_segment(s, begin, begin + i)
if ip_segment != -1:
path.append(str(ip_segment))
self.__dfs(s, size, split_times + 1, begin + i + 1, path, res)
path.pop()
def __judge_if_ip_segment(self, s, left, right):
size = right - left + 1
if size > 1 and s[left] == '0':
return -1
res = 0
for i in range(left, right + 1):
res = res * 10 + ord(s[i]) - ord('0')
if res > 255:
return - 1
return res
参考代码 2:(与参考代码 1 不同之处只在于剪枝少判断,而且也是先判断截取的 ip 段是否合法,然后用截取函数截取字符串,执行结果上会快一些)
Java 代码:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<String> restoreIpAddresses(String s) {
int len = s.length();
List<String> res = new ArrayList<>();
if (len > 12 || len < 4) {
return res;
}
Deque<String> path = new ArrayDeque<>(4);
dfs(s, len, 0, 4, path, res);
return res;
}
// 需要一个变量记录剩余多少段还没被分割
private void dfs(String s, int len, int begin, int residue, Deque<String> path, List<String> res) {
if (begin == len) {
if (residue == 0) {
res.add(String.join(".", path));
}
return;
}
for (int i = begin; i < begin + 3; i++) {
if (i >= len) {
break;
}
if (residue * 3 < len - i) {
continue;
}
if (judgeIpSegment(s, begin, i)) {
String currentIpSegment = s.substring(begin, i + 1);
path.addLast(currentIpSegment);
dfs(s, len, i + 1, residue - 1, path, res);
path.removeLast();
}
}
}
private boolean judgeIpSegment(String s, int left, int right) {
int len = right - left + 1;
if (len > 1 && s.charAt(left) == '0') {
return false;
}
int res = 0;
while (left <= right) {
res = res * 10 + s.charAt(left) - '0';
left++;
}
return res >= 0 && res <= 255;
}
}
复杂度分析:
- 时间复杂度:因为这个问题限制在有效 IP 段内,因此需要截取和检查的次数有上限,分析清楚这个复杂度在我的能力范围之外(欢迎大家指导)。很多回溯问题的复杂度分析都比较“复杂”,所以我选择暂时搁浅。
- 空间复杂度:
O
(
1
)
O(1)
O(1),也是由于这个问题限制在有效 IP 段内,树最多
4层,保存的结果集也是有限个。