激光SLAM总结——Fast LIO / Fast LIO2 / Faster LIO
在之前的工作中有接触过LOAM,最近在工作中又接触到Faster LIO相关的工作,于是想着对Fast LIO / Fast LIO2 / Faster LIO这一系列工作进行一个简单的总结,以加深自己对激光SLAM算法的理解,之前总结过的一些和激光SLAM算法相关的博客还有,感兴趣的同学可以一起学习讨论:
激光SLAM总结——VLOAM / LIMO算法解析
激光SLAM总结——LIO-Mapping / LIOM / LINS / LIO-SAM算法解析
1. Fast LIO
FAST LIO是2021年提出的一个激光和IMU紧耦合迭代卡尔曼滤波框架,论文的贡献主要是提供了一个新的卡尔曼增益计算公式,新公式不依赖于测量维度,仅依赖于状态维度,从而达到高效的计算
Fast LIO是基于LINS进行进一步优化,那么LINS有什么问题呢?LINS是紧耦合框架,点云构建的残差被直接写入了观测方程,点云残差构建如下: f i ( x b k + 1 b k ) = { ∣ ( p ^ i l k − p a l k ) × ( p ^ i l k − p b I k ) ∣ ∣ p a l k − p b l k ∣ if p i l k + 1 ∈ F e ∣ ( p ^ i k − p a l ) T ( ( p a k − p b k ) × ( p a l − p c l ) ) ∣ ∣ ( p a l k − p b l k ) × ( p a l k − p c l c ) ∣ if p i l k + 1 ∈ F p f_{i}\left(\mathbf{x}_{b_{k+1}}^{b_{k}}\right)=\left\{\begin{array}{cl} \frac{\left|\left(\hat{\mathbf{p}}_{i}^{l_{k}}-\mathbf{p}_{a}^{l_{k}}\right) \times\left(\hat{\mathbf{p}}_{i}^{l_{k}}-\mathbf{p}_{b}^{I_{k}}\right)\right|}{\left|\mathbf{p}_{a}^{l_{k}}-\mathbf{p}_{b}^{l_{k}}\right|} & \text { if } \mathbf{p}_{i}^{l_{k+1}} \in \mathbb{F}_{e} \\ \frac{\left|\left(\hat{\mathbf{p}}_{i}^{k}-\mathbf{p}_{a}^{l}\right)^{T}\left(\left(\mathbf{p}_{a}^{k}-\mathbf{p}_{b}^{k}\right) \times\left(\mathbf{p}_{a}^{l}-\mathbf{p}_{c}^{l}\right)\right)\right|}{\left|\left(\mathbf{p}_{a}^{l_{k}}-\mathbf{p}_{b}^{l_{k}}\right) \times\left(\mathbf{p}_{a}^{l_{k}}-\mathbf{p}_{c}^{l_{c}}\right)\right|} & \text { if } \mathbf{p}_{i}^{l_{k+1}} \in \mathbb{F}_{p} \end{array}\right. fi(xbk+1bk)=⎩ ⎨ ⎧ palk−pblk (p^ilk−palk)×(p^ilk−pbIk) (palk−pblk)×(palk−pclc) (p^ik−pal)T((pak−pbk)×(pal−pcl)) if pilk+1∈Fe if pilk+1∈Fp残差的维度和点的数量相关,假设残差的维度为 m m m,在计算卡尔曼增益过程中会计算残差相对状态变量的线性化矩阵 H k \mathbf{H}_{k} Hk,其维度为 m × n m \times n m×n,其中 n n n为状态变量维度,进而计算 H k P k H k T + V \mathbf{H}_{k}\mathbf{P}_{k}\mathbf{H}_{k}^T+\mathbf{V} HkPkHkT+V时维度将变为 m × m m \times m m×m,在计算卡尔曼增益的过程中是需要对该矩阵进行求逆,可以预见当用于计算残差的特征点数量特别大时,计算卡尔曼增益也会变得相对耗时,在Fast-LIO就是通过SMW恒等式解决了该问题,使得计算卡尔曼增益不再依赖于观测维度,下面我们进一步看看具体是怎么做的
1.1 总体框架
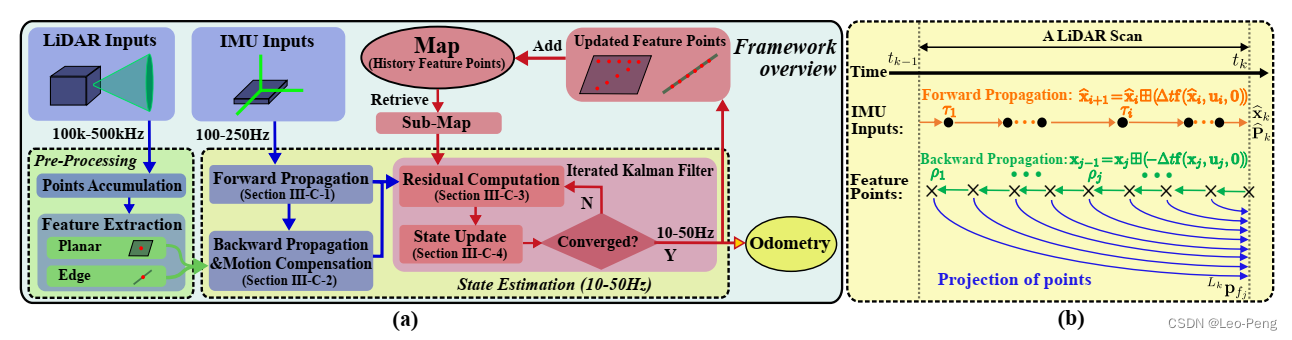
Fast LIO的总体框架如下图所示:
大致流程是将激光雷达输入到特征提取模块,可获得平面和边缘特征,将提取后的特征和IMU测量值进行状态估计,输出
10
H
Z
10HZ
10HZ到
50
H
Z
50HZ
50HZ的状态估计结果,并根据状态估计结果将特征点注册到全局地图。
1.2 Iterated Kalman Filter
下面进行Fast LIO的公式推导:
假设IMU系为Body系,激光系到IMU系为刚体变换 I T L = ( I R L , I p L ) { }^I \mathbf{T}_L=\left({ }^I \mathbf{R}_L,{ }^I \mathbf{p}_L\right) ITL=(IRL,IpL)
IMU的连续运动学方程为: G p ˙ I = G v I , G v ˙ I = G R I ( a m − b a − n a ) + G g , G g ˙ = 0 G R ˙ I = G R I ∣ ω m − b ω − n ω ⌋ Λ , b ˙ ω = n b ω , b ˙ a = n b a \begin{aligned}{ }^G \dot{\mathbf{p}}_I & ={ }^G \mathbf{v}_I,{ }^G \dot{\mathbf{v}}_I={ }^G \mathbf{R}_I\left(\mathbf{a}_m-\mathbf{b}_{\mathrm{a}}-\mathbf{n}_{\mathrm{a}}\right)+{ }^G \mathbf{g},{ }^G \dot{\mathrm{g}}=\mathbf{0} \\ { }^G \dot{\mathbf{R}}_I & \left.={ }^G \mathbf{R}_I \mid \boldsymbol{\omega}_m-\mathbf{b}_{\boldsymbol{\omega}}-\mathbf{n}_\omega\right\rfloor \Lambda, \dot{\mathbf{b}}_{\boldsymbol{\omega}}=\mathbf{n}_{\mathbf{b} \boldsymbol{\omega}}, \dot{\mathbf{b}}_{\mathbf{a}}=\mathbf{n}_{\mathbf{b a}}\end{aligned} Gp˙IGR˙I=GvI,Gv˙I=GRI(am−ba−na)+Gg,Gg˙=0=GRI∣ωm−bω−nω⌋Λ,b˙ω=nbω,b˙a=nba其中 G p I { }^G \mathbf{p}_I GpI, G R I { }^G \mathbf{R}_I GRI是IMU的位置和姿态, a m \mathbf{a}_m am, ω m \boldsymbol{\omega}_m ωm为IMU的测量, b a \mathbf{b}_{\mathbf{a}} ba, b ω \mathbf{b}_\omega bω为随机游走高斯噪声
IMU的离散运动学方程为 x i + 1 = x i ⊞ ( Δ t f ( x i , u i , w i ) ) \mathbf{x}_{i+1}=\mathbf{x}_i \boxplus\left(\Delta t \mathbf{f}\left(\mathbf{x}_i, \mathbf{u}_i, \mathbf{w}_i\right)\right) xi+1=xi⊞(Δtf(xi,ui,wi))其中: x ≐ [ G R I T G p I T G v I T b ω T b a T G g T ] T ∈ M \mathbf{x} \doteq\left[\begin{array}{llllll} { }^G \mathbf{R}_I^T & { }^G \mathbf{p}_I^T & { }^G \mathbf{v}_I^T & \mathbf{b}_{\boldsymbol{\omega}}^T & \mathbf{b}_{\mathbf{a}}^T & { }^G \mathbf{g}^T \end{array}\right]^T \in \mathcal{M} x≐[GRITGpITGvITbωTbaTGgT]T∈M u ≐ [ ω m T a m T ] T \mathbf{u} \doteq\left[\begin{array}{ll} \boldsymbol{\omega}_m^T & \mathbf{a}_m^T \end{array}\right]^T u≐[ωmTamT]T w ≐ [ n ω T n a T n b ω T n b a T ] T \mathbf{w} \doteq\left[\begin{array}{llll} \mathbf{n}_\omega^T & \mathbf{n}_{\mathrm{a}}^T & \mathbf{n}_{\mathrm{b} \boldsymbol{\omega}}^T & \mathbf{n}_{\mathrm{ba}}^T \end{array}\right]^T w≐[nωTnaTnbωTnbaT]T f ( x i , u i , w i ) = [ ω m i − b ω i − n ω i G v I i G R I i ( a m i − b a i − n a i ) + G g i n b ω i n b a i 0 3 × 1 ] \mathbf{f}\left(\mathbf{x}_i, \mathbf{u}_i, \mathbf{w}_i\right)=\left[\begin{array}{c} \boldsymbol{\omega}_{m_i}-\mathbf{b}_{\omega_i}-\mathbf{n}_{\omega_i} \\ { }^G \mathbf{v}_{I_i} \\ { }^G \mathbf{R}_{I_i}\left(\mathbf{a}_{m_i}-\mathbf{b}_{\mathbf{a}_i}-\mathbf{n}_{\mathbf{a}_i}\right)+{ }^G \mathbf{g}_i \\ \mathbf{n}_{\mathbf{b} \omega_i} \\ \mathbf{n}_{\mathbf{b a}_i} \\ \mathbf{0}_{3 \times 1} \end{array}\right] f(xi,ui,wi)= ωmi−bωi−nωiGvIiGRIi(ami−bai−nai)+Gginbωinbai03×1
下面迭代扩展卡尔曼滤波进行状态估计,定义误差状态如下: x ~ k − 1 ≐ x k − 1 ⊟ x ‾ k − 1 = [ δ θ T G p ~ I T G v ~ I T b ~ ω T b ~ a T G g ~ T ] T \widetilde{\mathbf{x}}_{k-1} \doteq \mathbf{x}_{k-1} \boxminus \overline{\mathbf{x}}_{k-1}=\left[\begin{array}{llllll} \delta \boldsymbol{\theta}^T & G \widetilde{\mathbf{p}}_I^T & G \widetilde{\mathbf{v}}_I^T & \tilde{\mathbf{b}}_{\boldsymbol{\omega}}^T & \tilde{\mathbf{b}}_{\mathbf{a}}^T & { }^G \widetilde{\mathbf{g}}^T \end{array}\right]^T x k−1≐xk−1⊟xk−1=[δθTGp ITGv ITb~ωTb~aTGg T]T其中, x k − 1 \mathbf{x}_{k-1} xk−1为真实状态, ⊟ x ‾ k − 1 \boxminus \overline{\mathbf{x}}_{k-1} ⊟xk−1为标称状态, x ~ k − 1 \widetilde{\mathbf{x}}_{k-1} x k−1为误差状态
前向传播流程如下: x ^ i + 1 = x ^ i ⊞ ( Δ t f ( x ^ i , u i , 0 ) ) ; x ^ 0 = x ‾ k − 1 . \widehat{\mathbf{x}}_{i+1}=\widehat{\mathbf{x}}_i \boxplus\left(\Delta t \mathbf{f}\left(\widehat{\mathbf{x}}_i, \mathbf{u}_i, \mathbf{0}\right)\right) ; \widehat{\mathbf{x}}_0=\overline{\mathbf{x}}_{k-1} \text {. } x i+1=x i⊞(Δtf(x i,ui,0));x 0=xk−1. 其中上述计算的是标称状态的传播,计算过程中不考虑的噪声,状态的协方差通过误差状态进行传播,并吸纳这部分噪声,如下,误差状态定位如下:: x ~ i + 1 = x i + 1 ⊟ x ^ i + 1 = ( x i ⊞ Δ t f ( x i , u i , w i ) ) ⊟ ( x ^ i ⊞ Δ t f ( x ^ i , u i , 0 ) ) ≃ ( 23 ) F x ~ x ~ i + F w w i . \begin{aligned} \widetilde{\mathbf{x}}_{i+1} & =\mathbf{x}_{i+1} \boxminus \widehat{\mathbf{x}}_{i+1} \\ & =\left(\mathbf{x}_i \boxplus \Delta t \mathbf{f}\left(\mathbf{x}_i, \mathbf{u}_i, \mathbf{w}_i\right)\right) \boxminus\left(\widehat{\mathbf{x}}_i \boxplus \Delta t \mathbf{f}\left(\widehat{\mathbf{x}}_i, \mathbf{u}_i, \mathbf{0}\right)\right) \\ & \stackrel{(23)}{\simeq} \mathbf{F}_{\tilde{\mathbf{x}}} \widetilde{\mathbf{x}}_i+\mathbf{F}_{\mathbf{w}} \mathbf{w}_i . \end{aligned} x i+1=xi+1⊟x i+1=(xi⊞Δtf(xi,ui,wi))⊟(x i⊞Δtf(x i,ui,0))≃(23)Fx~x i+Fwwi.其中: F x ‾ = [ Exp ( − ω ^ i Δ t ) 0 0 − A ( ω ^ i Δ t ) T Δ t 0 0 0 I I Δ t 0 0 0 − G R ^ I i ⌊ a ^ i ] ∧ Δ t 0 I 0 − G R ^ I i Δ t I Δ t 0 0 0 I 0 0 0 0 0 0 I 0 0 0 0 0 0 I ] \mathbf{F}_{\overline{\mathbf{x}}}=\left[\begin{array}{cccccc} \operatorname{Exp}\left(-\widehat{\boldsymbol{\omega}}_i \Delta t\right) & \mathbf{0} & \mathbf{0} & -\mathbf{A}\left(\widehat{\boldsymbol{\omega}}_i \Delta t\right)^T \Delta t & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} & \mathbf{I} \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ -{ }^G \widehat{\mathbf{R}}_{I_i}\left\lfloor\widehat{\mathbf{a}}_i\right]_{\wedge} \Delta t & \mathbf{0} & \mathbf{I} & \mathbf{0} & -{ }^G \widehat{\mathbf{R}}_{I_i} \Delta t & \mathbf{I} \Delta t \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \end{array}\right] Fx= Exp(−ω iΔt)0−GR Ii⌊a i]∧Δt0000I00000IΔtI000−A(ω iΔt)TΔt00I0000−GR IiΔt0I000IΔt00I F w = [ − A ( ω ^ i Δ t ) T Δ t 0 0 0 0 0 0 0 0 − G R ^ I i Δ t 0 0 0 0 I Δ t 0 0 0 0 I Δ t 0 0 0 0 ] \mathbf{F}_{\mathbf{w}}=\left[\begin{array}{cccc} -\mathbf{A}\left(\widehat{\boldsymbol{\omega}}_i \Delta t\right)^T \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & -{ }^G \widehat{\mathbf{R}}_{I_i} \Delta t & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{I} \Delta t & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \Delta t \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \end{array}\right] Fw= −A(ω iΔt)TΔt0000000−GR IiΔt000000IΔt000000IΔt0 那么协方差前向传播公式为: P ^ i + 1 = F x ‾ P ^ i F x ‾ T + F w Q F w T ; P ^ 0 = P ‾ k − 1 \widehat{\mathbf{P}}_{i+1}=\mathbf{F}_{\overline{\mathbf{x}}} \widehat{\mathbf{P}}_i \mathbf{F}_{\overline{\mathbf{x}}}^T+\mathbf{F}_{\mathbf{w}} \mathbf{Q} \mathbf{F}_{\mathbf{w}}^T ; \widehat{\mathbf{P}}_0=\overline{\mathbf{P}}_{k-1} P i+1=FxP iFxT+FwQFwT;P 0=Pk−1在完成IMU前向传播后,一方面会根据前向传播的结果对激光点云去运动畸变,另一方面会使用激光点云计算残差构建观测方程。
Fast LIO中使用的是点到面的残差,残差 z j κ \mathbf{z}_j^\kappa zjκ计算如下: G p ^ f j κ = G T ^ I k κ I T L L k p f j ; j = 1 , ⋯ , m . { }^G \widehat{\mathbf{p}}_{f_j}^\kappa={ }^G \widehat{\mathbf{T}}_{I_k}^\kappa{ }^I \mathbf{T}_L{ }^{L_k} \mathbf{p}_{f_j} ; j=1, \cdots, m . Gp fjκ=GT IkκITLLkpfj;j=1,⋯,m. z j κ = G j ( G p ^ f j κ − G q j ) \mathbf{z}_j^\kappa=\mathbf{G}_j\left({ }^G \widehat{\mathbf{p}}_{f_j}^\kappa-{ }^G \mathbf{q}_j\right) zjκ=Gj(Gp fjκ−Gqj)其中 κ \kappa κ为迭代卡尔曼滤波中的迭代次数。为了将残差 z j κ \mathbf{z}_j^\kappa zjκ直接加入滤波过程,因此需要对残差进行线性化,线性化过程如下,如果将点云测量过程中的噪声移除的话,测量方程如下: 0 = h j ( x k L j n f j ) = G j ( G T I k I k T ˇ I j I T L ( L j p f j − L j n f j ) − G q j ) \mathbf{0}=\mathbf{h}_j\left(\mathbf{x}_k{ }^{L_j} \mathbf{n}_{f_j}\right)=\mathbf{G}_j\left({ }^G \mathbf{T}_{I_k}{ }^{I_k} \check{\mathbf{T}}_{I_j}{ }^I \mathbf{T}_L\left({ }^{L_j} \mathbf{p}_{f_j}-{ }^{L_j} \mathbf{n}_{f_j}\right)-{ }^G \mathbf{q}_j\right) 0=hj(xkLjnfj)=Gj(GTIkIkTˇIjITL(Ljpfj−Ljnfj)−Gqj)进行一阶近似后: 0 = h j ( x k , L j n f j ) ≃ h j ( x ^ k κ , 0 ) + H j κ x ~ k κ + v j = z j κ + H j κ x ~ k κ + v j \begin{aligned} \mathbf{0} & =\mathbf{h}_j\left(\mathbf{x}_k,{ }^{L_j} \mathbf{n}_{f_j}\right) \simeq \mathbf{h}_j\left(\widehat{\mathbf{x}}_k^\kappa, \mathbf{0}\right)+\mathbf{H}_j^\kappa \widetilde{\mathbf{x}}_k^\kappa+\mathbf{v}_j \\ & =\mathbf{z}_j^\kappa+\mathbf{H}_j^\kappa \widetilde{\mathbf{x}}_k^\kappa+\mathbf{v}_j \end{aligned} 0=hj(xk,Ljnfj)≃hj(x kκ,0)+Hjκx kκ+vj=zjκ+Hjκx kκ+vj其中 x k = x ^ k κ ⊞ x ~ k κ \mathbf{x}_k=\widehat{\mathbf{x}}_k^\kappa \boxplus \widetilde{\mathbf{x}}_k^\kappa xk=x kκ⊞x kκ, H j κ \mathbf{H}_j^\kappa Hjκ是 h j ( x ^ k κ ⊞ x ~ k κ , L j n f j ) \mathbf{h}_j\left(\widehat{\mathbf{x}}_k^\kappa \boxplus \widetilde{\mathbf{x}}_k^\kappa,{ }^{L_j} \mathbf{n}_{f_j}\right) hj(x kκ⊞x kκ,Ljnfj)相对误差状态 x ~ k κ \widetilde{\mathbf{x}}_k^\kappa x kκ的雅可比,卡尔曼增益计算如下: K = P H T ( H P H T + R ) − 1 \mathbf{K}=\mathbf{P} \mathbf{H}^T\left(\mathbf{H} \mathbf{P} \mathbf{H}^T+\mathbf{R}\right)^{-1} K=PHT(HPHT+R)−1其中 H = [ H 1 κ T , ⋯ , H m κ T ] T \mathbf{H}=\left[\mathbf{H}_1^{\kappa^T}, \cdots, \mathbf{H}_m^{\kappa^T}\right]^T H=[H1κT,⋯,HmκT]T, R = diag ( R 1 , ⋯ R m ) \mathbf{R}=\operatorname{diag}\left(\mathbf{R}_1, \cdots \mathbf{R}_m\right) R=diag(R1,⋯Rm), z k κ = [ z 1 κ T , ⋯ , z m κ T ] T \mathbf{z}_k^\kappa=\left[\mathbf{z}_1^{\kappa^T}, \cdots, \mathbf{z}_m^{\kappa^T}\right]^T zkκ=[z1κT,⋯,zmκT]T,正如前面提到的 H P H T + R \mathbf{H} \mathbf{P} \mathbf{H}^T+\mathbf{R} HPHT+R的维度和观测维度相关,本文提出了一个新的卡尔曼增益计算公式: K = ( H T R − 1 H + P − 1 ) − 1 H T R − 1 \mathbf{K}=\left(\mathbf{H}^T \mathbf{R}^{-1} \mathbf{H}+\mathbf{P}^{-1}\right)^{-1} \mathbf{H}^T \mathbf{R}^{-1} K=(HTR−1H+P−1)−1HTR−1在这个公式中只需要进行两次求逆,但是求逆的维度都是状态变量的维度,状态变量的维度远小于测量维度,因此计算量也会小很多。公式的具体推导流程如下,根据SMW恒等式有: ( P − 1 + H T R − 1 H ) − 1 = P − P H T ( H P T + R ) − 1 H P \left(\mathbf{P}^{-1}+\mathbf{H}^T \mathbf{R}^{-1} \mathbf{H}\right)^{-1}=\mathbf{P}-\mathbf{P H}^T\left(\mathbf{H P}^T+\mathbf{R}\right)^{-1} \mathbf{H} \mathbf{P} (P−1+HTR−1H)−1=P−PHT(HPT+R)−1HP因此我们有: K = ( H T R − 1 H + P − 1 ) − 1 H T R − 1 = P H T R − 1 − P H T ( H P H T + R ) − 1 H P H T R − 1 \begin{aligned} \mathbf{K} & =\left(\mathbf{H}^T \mathbf{R}^{-1} \mathbf{H}+\mathbf{P}^{-1}\right)^{-1} \mathbf{H}^T \mathbf{R}^{-1} \\ & =\mathbf{P H}^T \mathbf{R}^{-1}-\mathbf{P} \mathbf{H}^T\left(\mathbf{H} \mathbf{P} \mathbf{H}^T+\mathbf{R}\right)^{-1} \mathbf{H} \mathbf{P} \mathbf{H}^T \mathbf{R}^{-1} \end{aligned} K=(HTR−1H+P−1)−1HTR−1=PHTR−1−PHT(HPHT+R)−1HPHTR−1注意到 H P H T R − 1 = ( H P H T + R ) R − 1 − I . \mathbf{H} \mathbf{P} \mathbf{H}^T \mathbf{R}^{-1}=\left(\mathbf{H} \mathbf{P} \mathbf{H}^T+\mathbf{R}\right) \mathbf{R}^{-1}-\mathbf{I} . HPHTR−1=(HPHT+R)R−1−I.因此我们可以获得: K = P H T R − 1 − P H T R − 1 + P H T ( H P T + R ) − 1 = P H T ( H P T + R ) − 1 . \begin{aligned} \mathbf{K} & =\mathbf{P} \mathbf{H}^T \mathbf{R}^{-1}-\mathbf{P} \mathbf{H}^T \mathbf{R}^{-1}+\mathbf{P} \mathbf{H}^T\left(\mathbf{H P}^T+\mathbf{R}\right)^{-1} \\ & =\mathbf{P H}^T\left(\mathbf{H P}^T+\mathbf{R}\right)^{-1} . \end{aligned} K=PHTR−1−PHTR−1+PHT(HPT+R)−1=PHT(HPT+R)−1.计算完卡尔曼增益后,进一步我们就可以获得更新后的误差状态和协方差: x ^ k κ + 1 = x ^ k κ ⊞ ( − K z k κ − ( I − K H ) ( J κ ) − 1 ( x ^ k κ ⊟ x ^ k ) ) \widehat{\mathbf{x}}_k^{\kappa+1}=\widehat{\mathbf{x}}_k^\kappa \boxplus\left(-\mathbf{K z}_k^\kappa-(\mathbf{I}-\mathbf{K} \mathbf{H})\left(\mathbf{J}^\kappa\right)^{-1}\left(\hat{\mathbf{x}}_k^\kappa \boxminus \widehat{\mathbf{x}}_k\right)\right) x kκ+1=x kκ⊞(−Kzkκ−(I−KH)(Jκ)−1(x^kκ⊟x k))当迭代收敛后标称状态更新为: x ‾ k = x ^ k κ + 1 , P ‾ k = ( I − K H ) P \overline{\mathbf{x}}_k=\widehat{\mathbf{x}}_k^{\kappa+1}, \overline{\mathbf{P}}_k=(\mathbf{I}-\mathbf{K H}) \mathbf{P} xk=x kκ+1,Pk=(I−KH)P以上就完成了Fast LIO的推导过程。
1.3 实验结果
作者在论文中比较了Fast LIO和LINS的效果,在使用相同数据集的前提下而LINS平均每帧激光提取特征点147个需要34.5ms,Fast LIO平均每帧激光提取特征点784个,用7.3ms的平均处理速度并取得了更高的精度。
2. Fast LIO2
Fast LIO2发表于2021年,是在Fast LIO上进一步优化的一篇工作,其主要贡献是:(1)直接将原始点注册到地图而不提取特征,这样有助于提供整个系统的准确性;(2)通过增量k-d树结构ikd-Tree维护映射,该结构支持增量插入、删除和动态重新平衡,与现有的动态数据结构相比有更优越的整体性能
2.1 总体框架
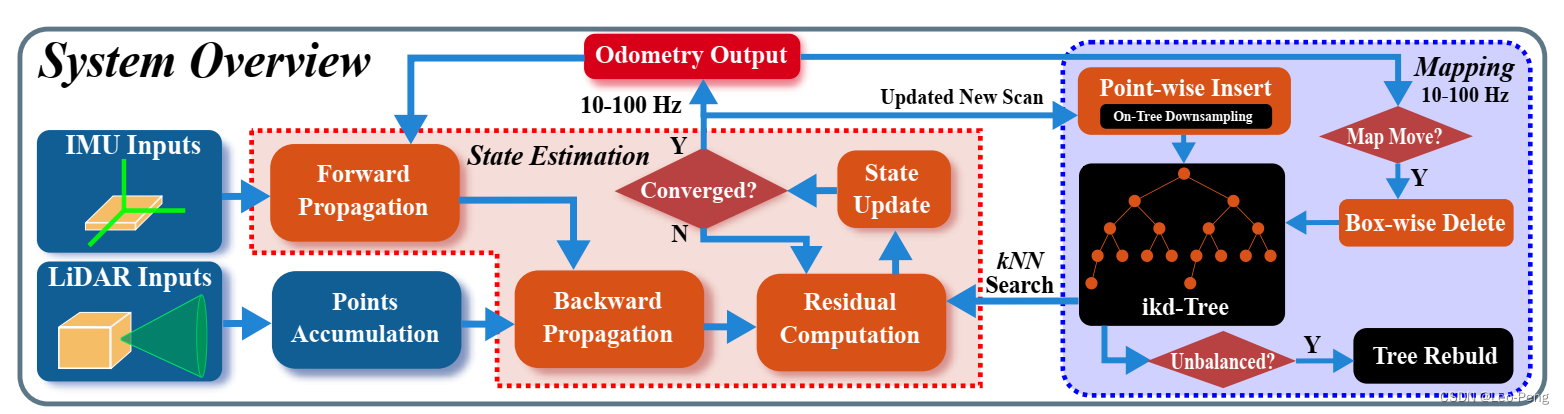
Fast-LIO2的整体框架如下:
其中State Estimation部分和Fast-LIO是基本一致的,下面我们主要总结下区别较大的Mapping部分
2.2 ikd-Tree
2.2.1 Map Management
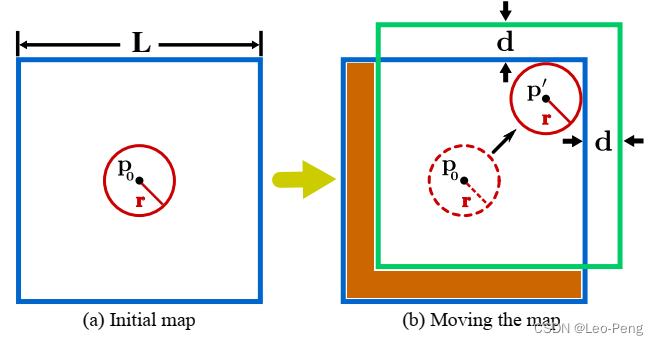
- 为了保证地图大小是可控的,只有在距离当前帧一定范围内的局部地图才会被保留,如下图所示:
在图(a)中,Body系位于 P 0 P_0 P0位置,初始化维护地图范围长度为 L L L,即蓝色方框内的区域;在图(b)中,当Body系移动到 P ′ P' P′时,维护地图范围将从蓝色方框的区域移动到绿色方框的区域。其中 r = γ R r=\gamma R r=γR, R R R为激光的FOV范围, γ \gamma γ为大于1的参与, d = ( γ − 1 ) R d=(\gamma-1) R d=(γ−1)R。
2.2.2 Tree Structure and Construction
- ikd-Tree是一个二分搜索树,和当前很多k-d树只在leaf nodes存储点的结构不同,ikd-Tree会在leaf nodes和internal nodes都对点进行存储;
- 在ikd-Tree中一个point只和一个node关联,point相关的属性存储在node上;
- ikd-Tree的数据结构如下图所示:
其中axis为用来进行空间划分的轴,treesize用于记录用当前节点为根节点的子节点的数量,invalidnum用于记录子节点被删除的节点的数量,如果点从地图中被删除,那么对应的节点的deleted标志位将被置为true,如果所有的子节点都已经被删除,那么treedeleted标注位将被置为true,range用于记录所有子节点对应的点覆盖的范围,具体来说记录的是一个包括所有子节点对应的点的矩形的最大最小值坐标。 - ikd-Tree的构建过程和普通kd-Tree的构建过程类似:循环依序取数据点的各维度来作为切分维度,取数据点在该维度的中值作为切分超平面,将中值左侧的数据点挂在其左子树,将中值右侧的数据点挂在其右子树。 递归处理其子树,直至所有数据点挂载完毕
2.2.3 Increment Updates
-
Incremental Updates分为Point-wise操作和Box-wise操作,Point-wise指的是对一个点进行Insert、Delete或者Re-insert操作,Box-wise是对一个Box内的所有点进行Insert、Delete或者Re-insert操作
-
Point Insertion with On-tree Downsampling,对于Point插入操作算法如下:
Point插入过程中会伴随着On-tree Downsample的操作,假定Downsample的分辨率为 l l l,根据分辨率 l l l可以将空间划分为若干个的立方体 C D \mathbf{C}_D CD,新插入点 p \mathbf{p} p会计算属于哪个 C D \mathbf{C}_D CD,算法计算离 C D \mathbf{C}_D CD中心 p center \mathbf{p}_{\text {center }} pcenter 最近的点 P nearest \mathbf{P}_{\text {nearest}} Pnearest,然后将 C D \mathbf{C}_D CD里已经存在的点删除,然后将 P nearest \mathbf{P}_{\text {nearest}} Pnearest重新插入ikd-Tree。插入操作则是在ikd-Tree中递归地找到一个空节点,对于递归过程中涉及到的每一个非空节点会更新其节点属性。 -
Box-wise Delete using Lazy Labels,在删除过程中,节点并不会立即被删除,而是delete标志位和treedeleted标志位做延后删除,判断节点是否要删除的流程如下:
假定要删除的范围是 C O \mathbf{C}_O CO,根据节点的range属性获得的范围是 C T \mathbf{C}_T CT,如果 C O \mathbf{C}_O CO和 C T \mathbf{C}_T CT不存在交集,则直接返回,如果 C O \mathbf{C}_O CO完全包含 C T \mathbf{C}_T CT,则将 C T \mathbf{C}_T CT包含的所有节点全部删除,如果 C O \mathbf{C}_O CO包含部分 C T \mathbf{C}_T CT递归到子节点做进一步判断。
2.2.4 Re-balancing
- Balancing Criterion,ikd-Tree的子树在满足如下两个条件时会激活平衡过程
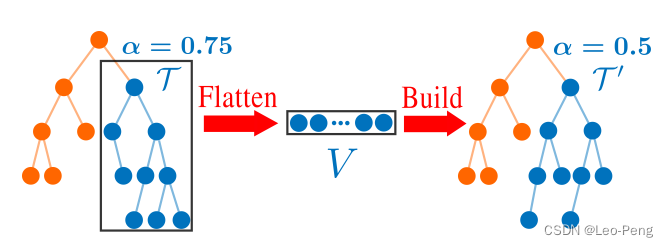
α \alpha α-balanced criterion: S ( T.leftchild ) < α bal ( S ( T ) − 1 ) S(\text { T.leftchild })<\alpha_{\text {bal }}(S(T)-1) S( T.leftchild )<αbal (S(T)−1) S ( T . r i g h t c h i l d ) < α bal ( S ( T ) − 1 ) S(T . r i g h t c h i l d)<\alpha_{\text {bal }}(S(T)-1) S(T.rightchild)<αbal (S(T)−1) α \alpha α-deleted criterion: I ( T ) < α d e l S ( T ) I(T)<\alpha_{d e l} S(T) I(T)<αdelS(T)其中 α b a l ∈ ( 0.5 , 1 ) \alpha_{b a l} \in(0.5,1) αbal∈(0.5,1), α del ∈ ( 0 , 1 ) \alpha_{\text {del }} \in(0,1) αdel ∈(0,1), S ( T ) S(T) S(T)指的是 T T T为根节点子树的节点个数, I ( T ) I(T) I(T)指的是以 T T T为根节点子树的无效节点的个数。前者是为了维持整颗树的最大高度,后者则是及时将无效节点移除以保证其他增量操作的高效。 - Rebuild & Parallel Rebuild,子树的重建过程如下图所示:
第一步是子树进行展平,在展平的过程中将无效节点进行移除,第二步对展平后的节点进行重建。如果子树的规模过大,重建过程可能会导致延迟,为了避免这个问题,作者提出重建算法如下:
算法会先判断需要重建的规模,如果规模小于某个阈值是直接在主线程中进行重建,如果规模过大,则新建一个线程进行重建,在新线程的重建过程中,会对Insert操作和Delete操作进行上锁,这些操作在主线程中进行缓存,在新线程重建完成后,再将这些操作在新线程复现一遍,因此新线程中重建的子树除了更加平衡,其他信息和主线程中的子树是一致的。
2.2.5 K-Nearest Neighbor Search
- 在ikd-Tree的数据结构中记录了每个子树的覆盖的范围,因为在ikd-Tree进行K-Nearest Neighbor Search过程中会建立一个priority queue,其中记录在搜索过程中到目标点的距离。在K-Nearest Neighbor Search过程中,遍历到每一个节点,会优先计算以这个节点为根节点的子树覆盖的范围到目标点的距离,如果距离大于priority queue中的最大值,那么则停止对这个子树的搜索,通过这种方式提高搜索效率。
2.3 实验结果
2.3.1 时间复杂度
- 对 C D = L x × L y × L z \mathbf{C}_D=L_x \times L_y \times L_z CD=Lx×Ly×Lz范围的Box-wise Delete和Search时间复杂度: O ( H ( n ) ) = { O ( log n ) if Δ min ⩾ α ( 2 3 ) ( ∗ ) O ( n 1 − a − b − c ) if Δ max ⩽ 1 − α ( 1 3 ) ( ∗ ∗ ) O ( n α ( 1 3 ) − Δ min − Δ med ) if ( ∗ ) and ( ∗ ∗ ) fail and Δ med < α ( 1 3 ) − α ( 2 3 ) O ( n α ( 2 3 ) − Δ min ) otherwise. O(H(n))= \begin{cases}O(\log n) & \text { if } \Delta_{\min } \geqslant \alpha\left(\frac{2}{3}\right)(*) \\ O\left(n^{1-a-b-c}\right) & \text { if } \Delta_{\max } \leqslant 1-\alpha\left(\frac{1}{3}\right)(* *) \\ O\left(n^{\alpha\left(\frac{1}{3}\right)-\Delta_{\min }-\Delta_{\text {med }}}\right) & \text { if }(*) \text { and }(* *) \text { fail and } \\ & \Delta_{\operatorname{med}}<\alpha\left(\frac{1}{3}\right)-\alpha\left(\frac{2}{3}\right) \\ O\left(n^{\alpha\left(\frac{2}{3}\right)-\Delta_{\min }}\right) & \text { otherwise. }\end{cases} O(H(n))=⎩ ⎨ ⎧O(logn)O(n1−a−b−c)O(nα(31)−Δmin−Δmed )O(nα(32)−Δmin) if Δmin⩾α(32)(∗) if Δmax⩽1−α(31)(∗∗) if (∗) and (∗∗) fail and Δmed<α(31)−α(32) otherwise. 其中 a = log n S x L x a=\log _n \frac{S_x}{L_x} a=lognLxSx, b = log n S y L y b=\log _n \frac{S_y}{L_y} b=lognLySy, c = log n S z L z c=\log _n \frac{S_z}{L_z} c=lognLzSz, Δ min \Delta_{\min } Δmin、 Δ med \Delta_{\text {med }} Δmed 、 Δ max \Delta_{\max } Δmax为 a a a、 b b b、 c c c中最小、中间和最大值
- Point Insertion with On-tree Downsampling时间复杂度为 O ( log n ) O(\log n) O(logn)
- 单线程re-building时间复杂度为 O ( n log n ) O(n \log n) O(nlogn),双线程re-building时间复杂度为 O ( n ) O(n) O(n)
- K-Nearest Neighbor Search时间复杂度为 O ( log n ) O(\log n) O(logn)
2.3.2 效率对比
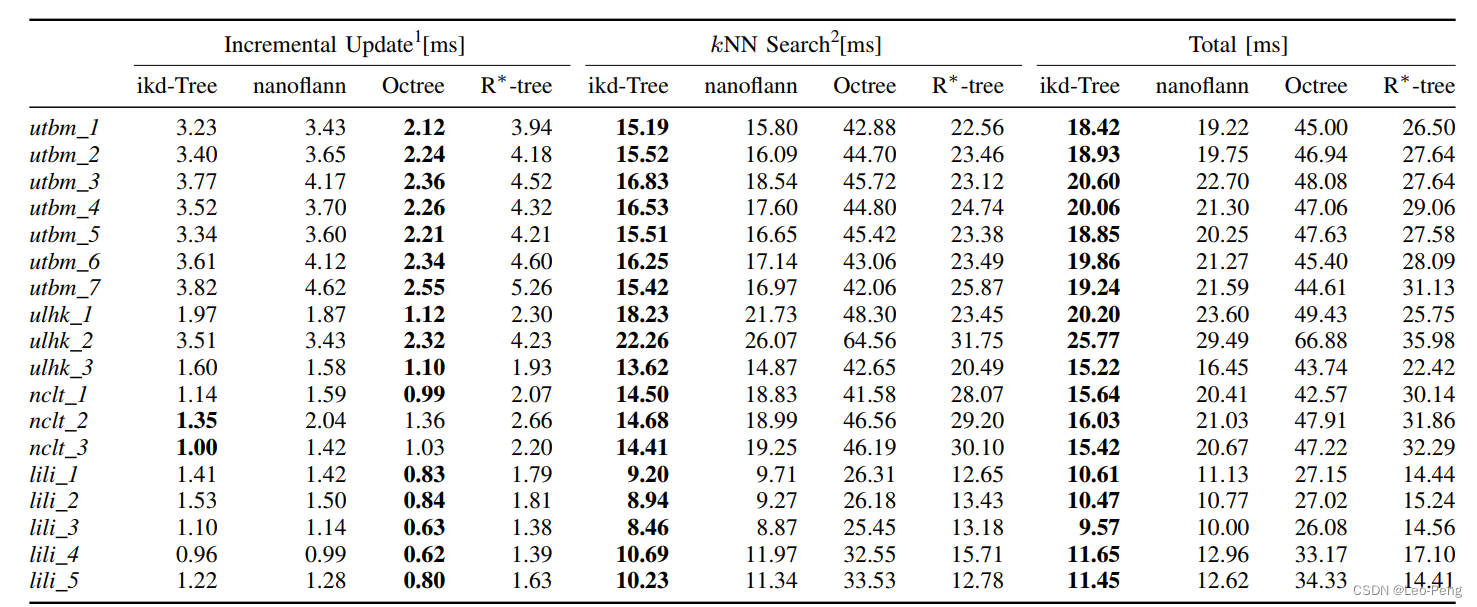
- ikd-Tree效率对比如下:
- Fast LIO2和其他SOTA方法效率对比如下:
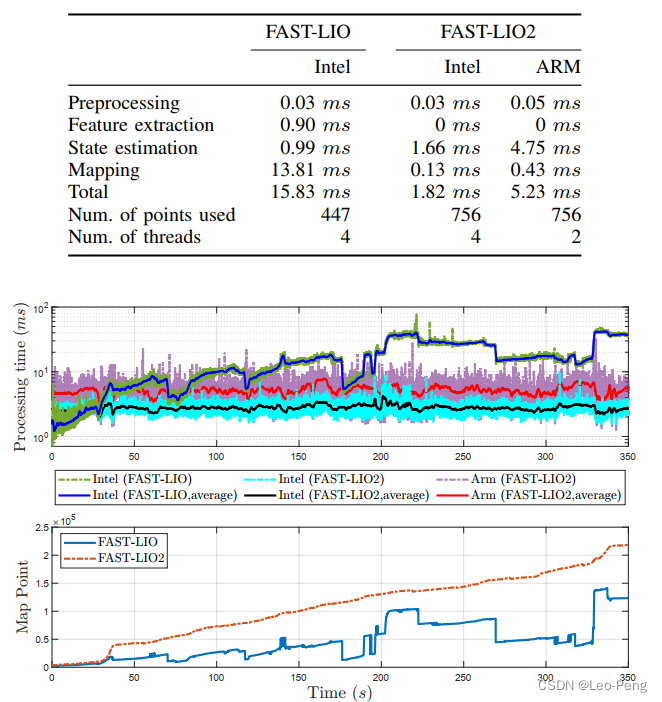
- Fast LIO和Fast LIO2的效率对比如下:
可以看出来,随着ikd-Tree的加入,Fast-LIO2的效率相对于Fast LIO会提高不少,以上就是对Fast LIO2的总结
3. Faster LIO
Faster LIO是高博团队发表于2022年的一篇论文,其主要贡献是是基于Fast LIO2将ikd-Tree的数据结构更新为iVox,进一步提高了算法效率,在知乎上有一篇高博对这个工作的介绍,感兴趣的同学可以参考Faster-LIO:快速激光IMU里程计,本篇只做一个简单总结
3.1 iVox
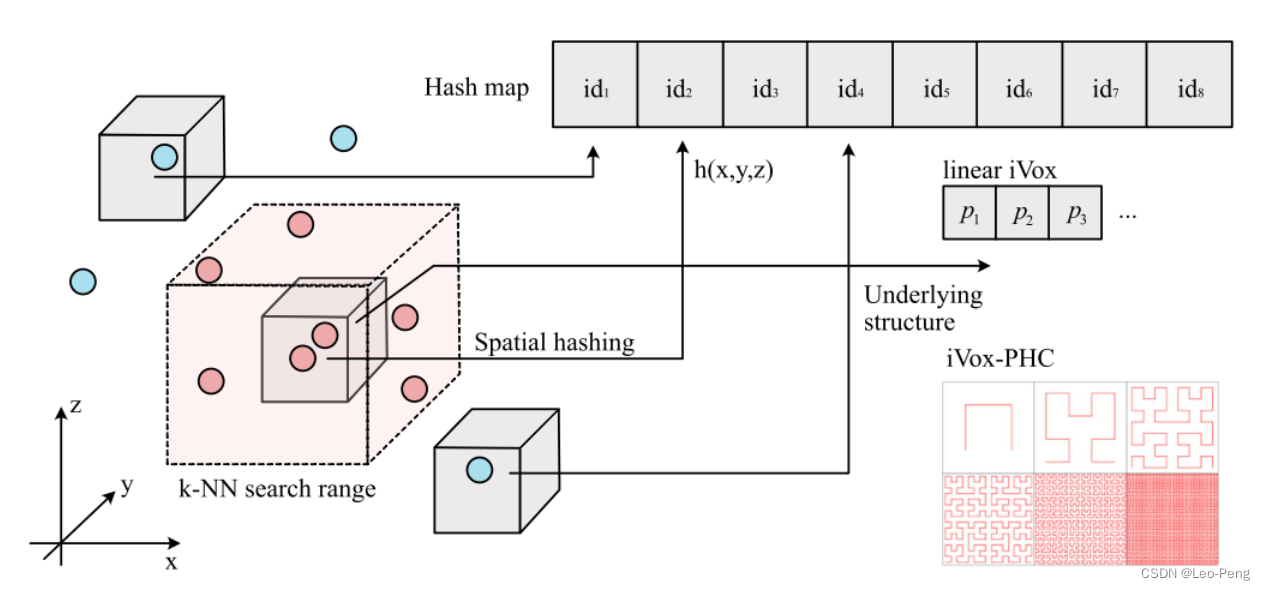
如下图是iVox的数据结构定义:
iVov的底层是一个空间哈希映射:
p
=
[
p
x
,
p
y
,
p
z
]
T
\mathbf{p}=\left[p_x, p_y, p_z\right]^T
p=[px,py,pz]T
v
=
1
s
[
p
x
,
p
y
,
p
z
]
T
\mathbf{v}=\frac{1}{s}\left[p_x, p_y, p_z\right]^T
v=s1[px,py,pz]T
i
d
v
=
hash
(
v
)
=
(
v
x
n
x
)
xor
(
v
y
n
y
)
xor
(
v
z
n
z
)
m
o
d
N
i d_v=\operatorname{hash}(v)=\left(v_x n_x\right) \text { xor }\left(v_y n_y\right) \text { xor }\left(v_z n_z\right) \bmod N
idv=hash(v)=(vxnx) xor (vyny) xor (vznz)modN其中
p
x
,
p
y
,
p
z
p_x, p_y, p_z
px,py,pz是空间点坐标,
s
s
s是栅格大小,
n
x
,
n
y
,
n
z
n_x, n_y, n_z
nx,ny,nz是大质数,因为质数不与其他数字存在公约数,可以减少因取模操作而产生的周期性模式,从而避免哈希冲突,
N
N
N是哈希表的大小。
在存储上,这些Voxel以Vector的数据结构进行存储或者使用PHC的数据结构进行存储,根据存储结构的不同分别称为Linear iVox或者iVox-PHC。
在查找K近邻时,先计算被查找的点落在哪个体素中,然后看预定义的范围内是否存在有效的iVox。如果有,就把这些iVox内部的点也考虑进来。我们在每个iVox内部查找至多K个最近邻,再进行合并即可。线性的iVox只须遍历内部点,然后进行部分排序,再进行汇总。PHC的iVox则可以根据空间填充曲线上的索引值来查找最近邻。,使用这种方式进行最近邻搜索其效率更高,精度会有所下降,但是对于点云匹配来讲这种精度已经足够。
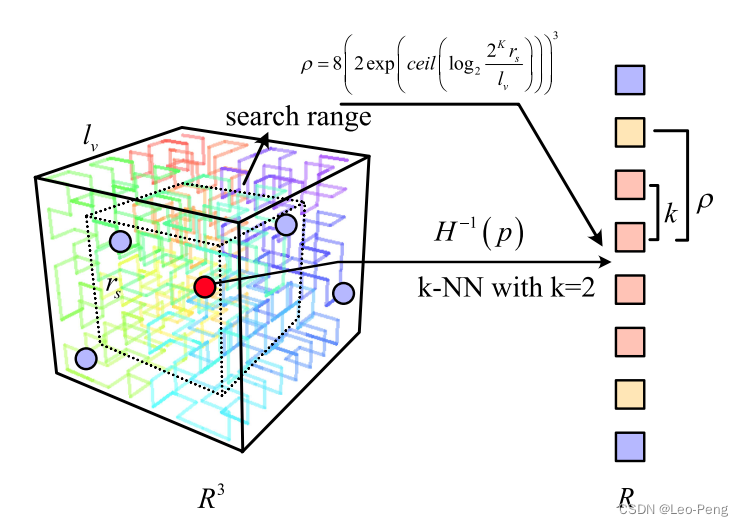
上述提到的PHC是一种建立高维数据与低维数据映射的方法,在查找最近邻时可以先把它看成这个iVox里的曲线上的ID,然后相关计算公式计算该ID周边的若干个近邻,如下图所示:
在论文中有补充到,由于Faster LIO会限制填入每个栅格的点的数量,因此PHC带来的收益并不是特别明显
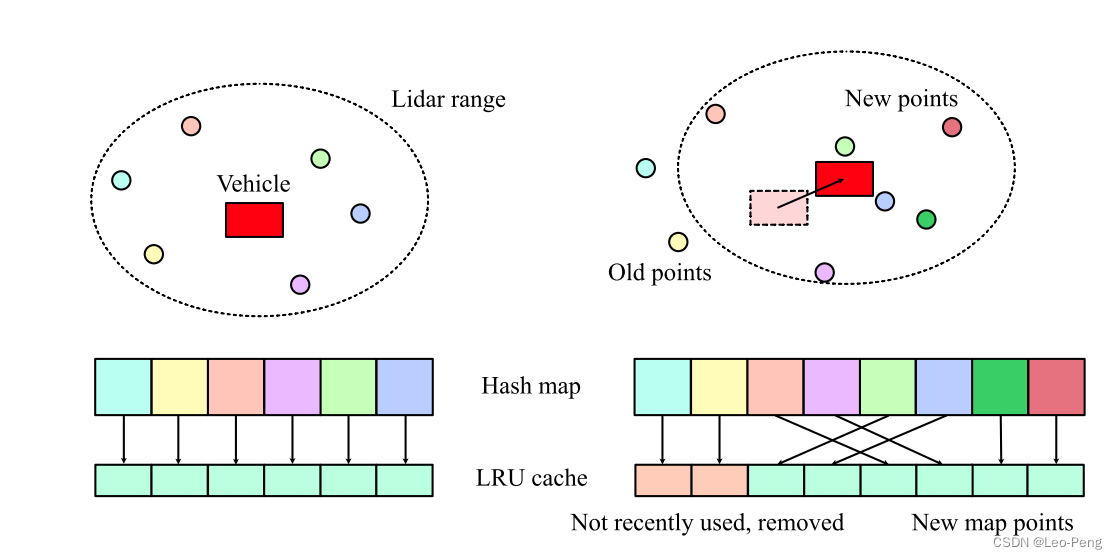
3.2 增量地图更新
在Fast LIO2中使用LUR缓存进行局部地图管理,在进行近邻搜索时,记录哪些体素是最近使用过的,那么不怎么使用的体素自然被移动到队尾。我们会设置一个局部地图的容量,超过最大容量时,就删除那些很久未使用的体素。删除操作是针对整个体素的,内部的点会被全部删除。这种局部地图缓存策略也会让局部地图跟随车辆运动,而实际操作的地方更少。如下图所示:
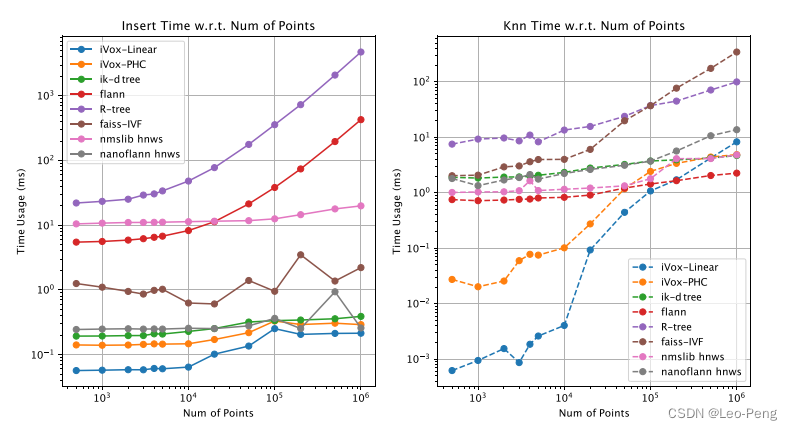
3.3 实验结果
如下是不同数据结构插入和最近邻搜索的耗时对比:
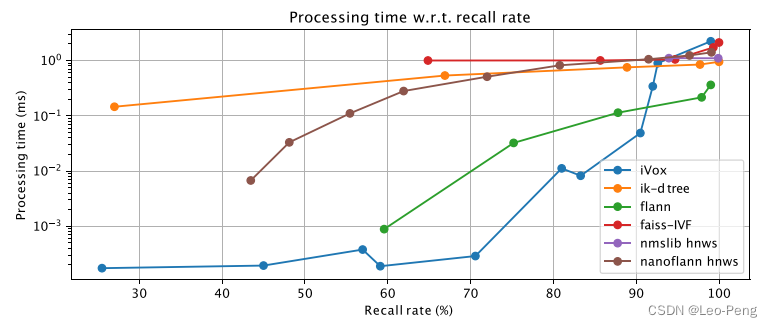
如下图是耗时和召回的关系曲线:
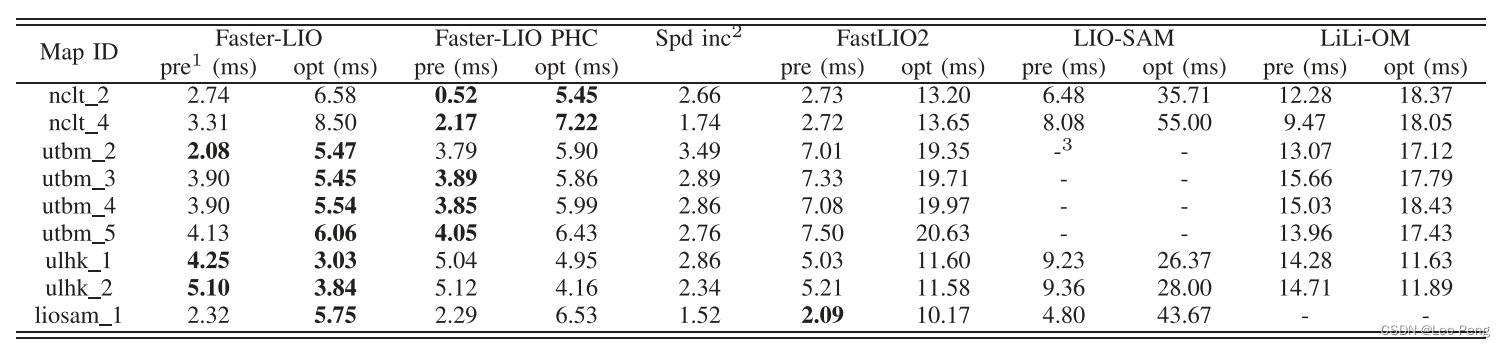
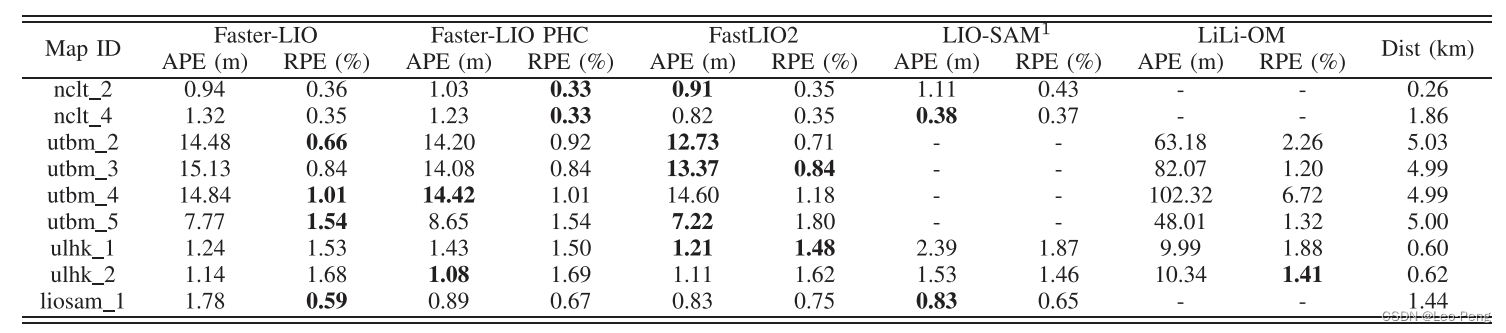
最后是Faster LIO整个系统耗时和精度对比:
可以看到,在相同的精度下Faster LIO确实取得了更快的速度,以上是对Faster LIO算法的简单总结