主要记录的是自己复习过程中遇到的零零散散、貌似很重要但又容易忘的知识点,总的来说比较基础,适合无聊的时候,一边摸鱼一边看。
数据科学中的数学基础
目录
1.标量
>> a=4 % 可以是整数a =4>> b=5.2 % 可以是小数b =5.2000>> x=-1.3 % 可以是负数x =-1.3000>> p=pi % 可以是某个常数p =3.1416>> y=inf% 可以是无穷大y =Inf>> z=‘M’ % 可以是一个字母z =‘M’>> n=NaN% 可以是非数 (Not a Number)n =NaN>> 3==5 % 可以是逻辑值ans =logical0
2.向量
b=linspace(1,10,5) % 以 linspace 在区间 1~10 之间生成 5 个元素的向量b =1.0000 3.2500 5.5000 7.7500 10.0000>> c=logspace(1,5,3) % 以 logspace 在区间 1~5 之间生成包含 3 个对数等分数据的行向量c =10 1000 100000
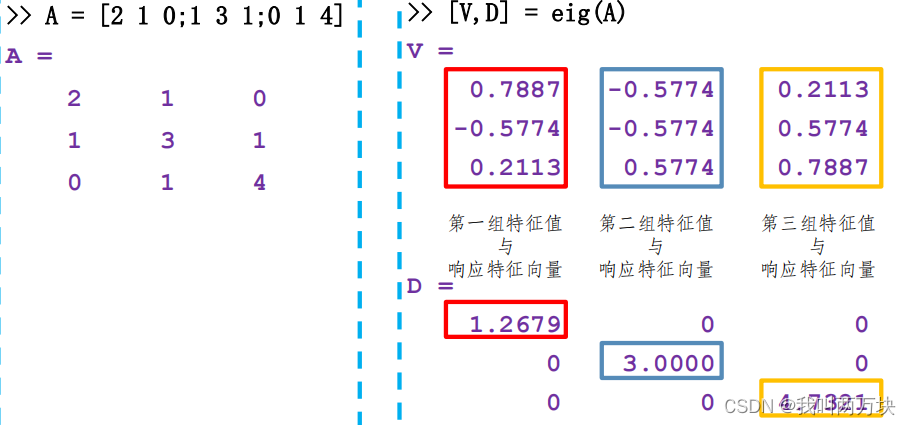
3.矩阵
tril(A) lower triangular matrix 下三角矩阵
triu(A) upper triangular matrix 上三角矩阵
A=[1,2,3;3,4,5;7,8,9]; %3x3 的矩阵R=triu(A,-1) % 以第 -1 条对角线分隔提取上三角R =1 2 33 4 50 8 9
diag(A) diagonal 对角线
eye(n) :生成n*n阶单位矩阵eye(m,n):生成m*n的单位矩阵,对角线元素为 1,其他为0eye(size(A)):生成一个矩阵A大小相同的单位 矩阵
size(A) 输出A矩阵的行数和列数。如果A多维,则输出每一维的个数(维数的长度)。
size(A,2) 输出A第二维的个数。
size(A,[1,3]) 输出A第一和第三维的个数。
size(A,2:4) 输出二到四维的个数。
以下函数与eye用法类似。
ones() 全1矩阵
zeros() 全0矩阵
rand() 随机矩阵 默认0~1的范围,可以通过n*rand()设置想要的范围。
randn() 生成n*n的服从标准正态分布的随机矩阵
加法:
矩阵和向量相加,即向量和矩阵的每一 行相加。这是一种隐式地复制向量到很多位置的方式,称为广播。
乘法
注意点乘 .* 和直接 * 的区别
dot(x,y) 标量点积
A = [4 -1 2]; B = [2 -2 -1];计算
A和B的点积。C = dot(A,B); C结果为 8,因为C = A(1)*B(1) + A(2)*B(2) + A(3)*B(3)
用cross() 表示叉积
使用点积验证
C是否与A和B垂直。dot(C,A)==0 & dot(C,B)==0
范数norm()
向量的1范数为各个元素的绝对值之和向量的2范数为各个元素的平方和的平方根向量的负无穷范数为所有元素的绝对值中最小的向量的正无穷范数为所有元素的绝对值中最大的向量的p范数为p次方和的p次方根
矩阵的1-范数(列和范数):矩阵的每一列上的元素绝对值先求和,再从中取最大值。(列和最大)norm(A,1);矩阵的2-范数(欧几里德范数,谱范数):矩阵 𝐴𝑇 𝐴 的最大特征值的平方根。矩阵的无穷范数(行范数):矩阵的每一行上的元 素绝对值先求和,再从中取最大值。(行和最大)norm(A,inf);矩阵的L0范数:非0元素的个数,通常用它来表示 稀疏,L0范数越小0元素越多,也就越稀疏。矩阵的L1范数:矩阵中的每个元素绝对值之和。矩阵的F范数:矩阵的各个元素平方之和再开平方根,它通常也叫做矩阵的L2范数。
rank(A) 求矩阵的秩
martixname 就是矩阵名称,包括好多乱七八糟的矩阵,什么对称正定矩阵'lehmer'、柯西矩阵balabala的,都可以输入。P1...是A1...的参数,例如p1等于11,matrixname是‘lehmer’,则返回一个11*11的对称正定矩阵给A1。
4.函数
求极限
>> syms x;>> y=arctan(x);>> limit(y,x,-inf);
求导数
diff(y) 求导数和差分的一个函数
diff(f,x) 对x求偏导diff(f,y) 对y求偏导
A = [1,4,5,7,9]
>> gradient(A)
ans =
3.0000 2.0000 1.5000 2.0000 2.0000
[Fx,Fy]=gradient(F),其中Fx为其水平方向上的梯度,Fy为其垂直方向上的梯度,Fx的第一列元素为原矩阵第二列与第一列元素之差,Fx的第二列元素为原矩阵第三列与第一列元素之差除以2,以此类推:Fx(i,j)=(F(i,j+1)-F(i,j-1))/2。最后一列则为最后两列之差。同理,可以得到Fy。
求概率密度函数
y = pdf('name',x,A)返回由'name'和分布参数A指定的单参数分布族的概率密度函数 (pdf),在x中的值处计算函数值。
一些分布函数的生成随机数
x=normrnd(mu,sigma,m,n)% 产生 m*n 阶均值为 mu ,方差为 sigma 正态分布的随机数矩阵x=unifrnd (a,b,m, n)% 产生 m*n 阶[ a , b ]均匀分布 U ( a , b )的随机数矩阵x=exprnd (mu,m, n)% 产生 m*n 阶均值为 mu 的指数分布的 随机数矩阵
magic
magic(n)返回由1到n2 的整数构成并且总行数和总列数相等的n×n矩阵。n的阶数必须是大于或等于3的标量才能创建有效的幻方矩阵。
函数区分传值和传地址的区别
传值
function [a,b]=myswap(x,y)a=y;b=x;
x=2;y=3;[m,n]=myswap(x,y);
function [a,b]=myswap(x,y)a=y;b=x;
>> x=2;>> y=3;>> [x,y] =myswap(x,y);
函数名=inline( ‘ 函数表达式 ’, ‘ 变量 1‘, ‘ 变量 2‘…… )
函数句柄变量=@(匿名函数输入参数) 匿名函数表达式
function fout=test(a,b,c)if nargin==1fout=a;elseif nargin==2fout=a+b;elseif nargin==3fout=(a*b*c)/2;end
>> fout=test(2) %nargin等于1,所以 fout=2fout =2>> fout=test(2,3,2) %nargin等于3 所以 。。。fout =6
global 变量名1 变量名2 变量名3...
5.元胞数组
可以包含各种类型和大小的数据的数组
6.文件
脚本文件和函数文件
脚本文件是可在命令行窗口直接执行的文件,也叫命令文件。函数文件是定义一个函数,不能直接执行,而必须以函数调用的方式来调用它。
>> edit test % 新建 test.m 文件
 于是A的值就变成100了
于是A的值就变成100了
7.分支语句
if 条件 1语句组 1elseif 条件 2语句组 2…elseif 条件 m语句组 melse语句组 nend
switch 表达式case 结果表 1语句组 1case 结果表 2语句组 2…case 结果表 m语句组 motherwise语句组 nend
注意,与C语言不同的是当任意一个分支的语句执行完后,整个 switch语句执行完毕。整个过程只会执行一个语 句组。
8.ps===
ax1 = axes('Position',[0.1 0.1 0.7 0.7]); 坐标(0.1,0.1) x,y轴宽度0.7
计算皮尔曼相关系数
x=[1;2;3]; y=[2;5;6];
r1=corr(x,y,'type','pearson');
r2=corrcoef(x,y);