快速排序介绍：

        快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

        这里我以升序为例。

        简单来说：一趟排序的本质实际上是将一个或几个数据放到它应该在的位置上。

例如：冒泡排序：每一趟都能将最大的数放到最后的位置。

插入排序：每次插入的数与前面比较，满足条件就插入，不满足就移动。

选择排序：每次选出最大/最小放到最前面或最后面。

堆排序：堆顶可以得到最值，与最后的元素交换后，使得这个最值排在正确位置。向下调整是为了下一次的排序。

而对于快速排序：是先用keyi（下标）标记数组中的一个位置，对于key=arr[keyi]，比它小的放到都它的左边，比它大的都放到它的右边，完成这样的一趟排序，key的位置就是它最终的位置。

然后再通过递归，对key左右分别进行快排。

Hoare方法实现

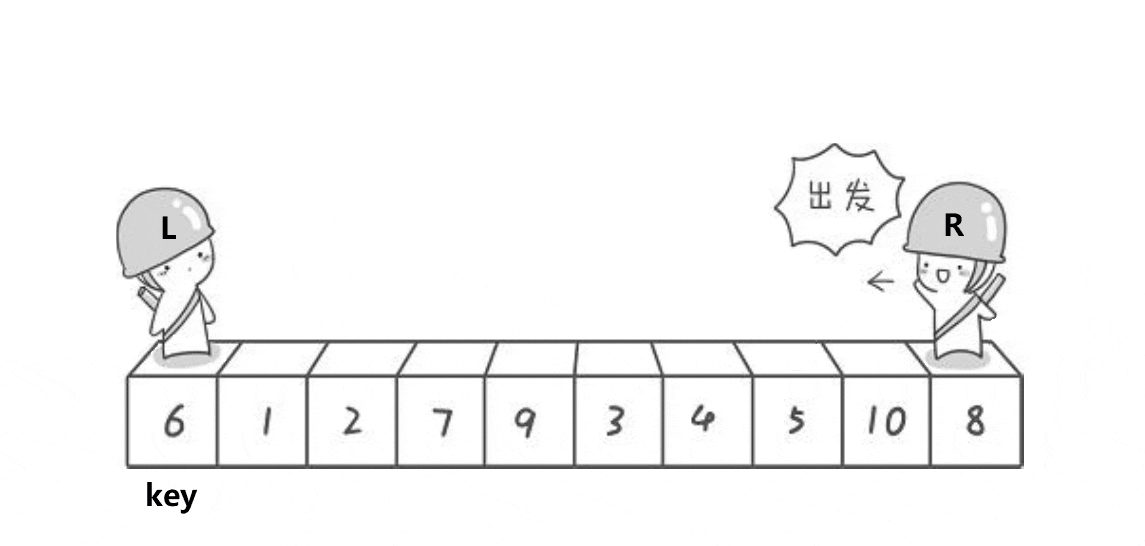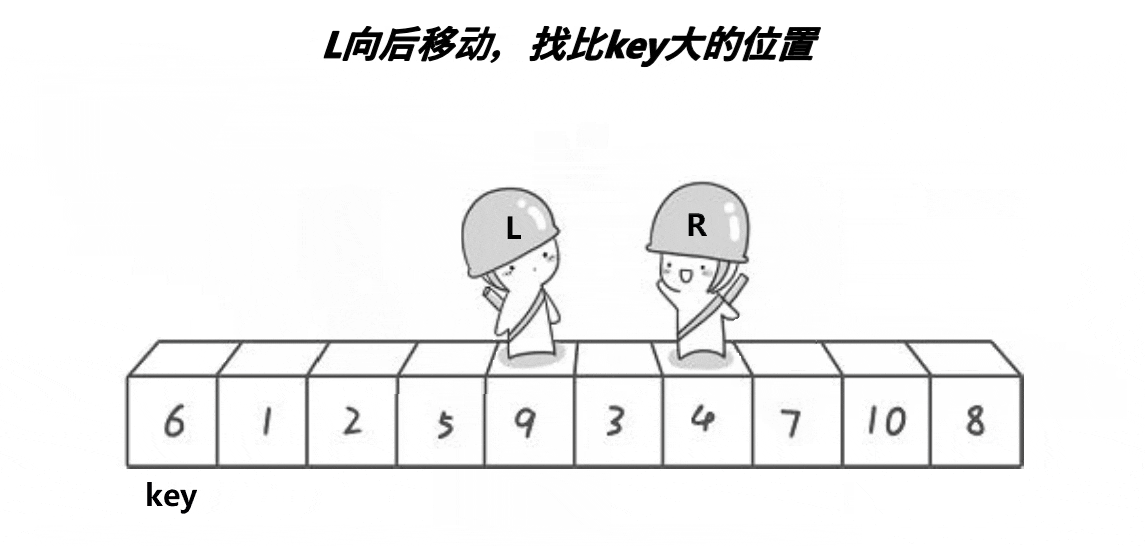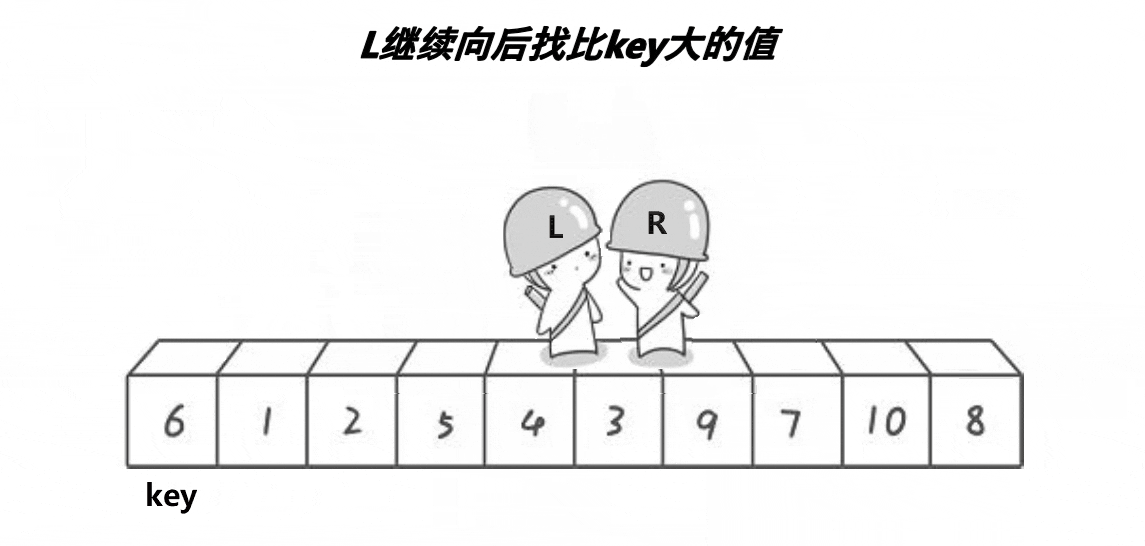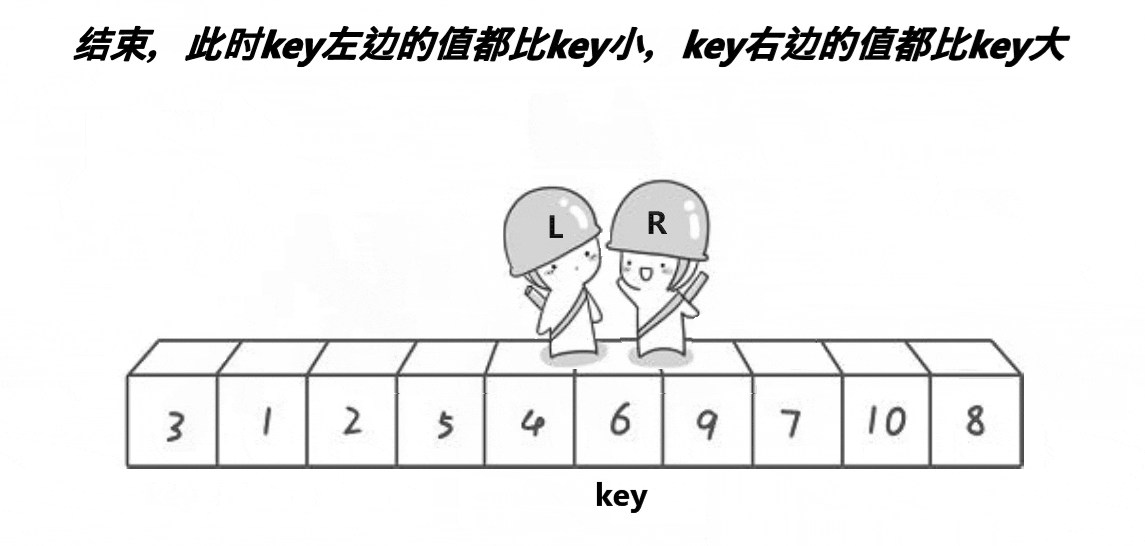
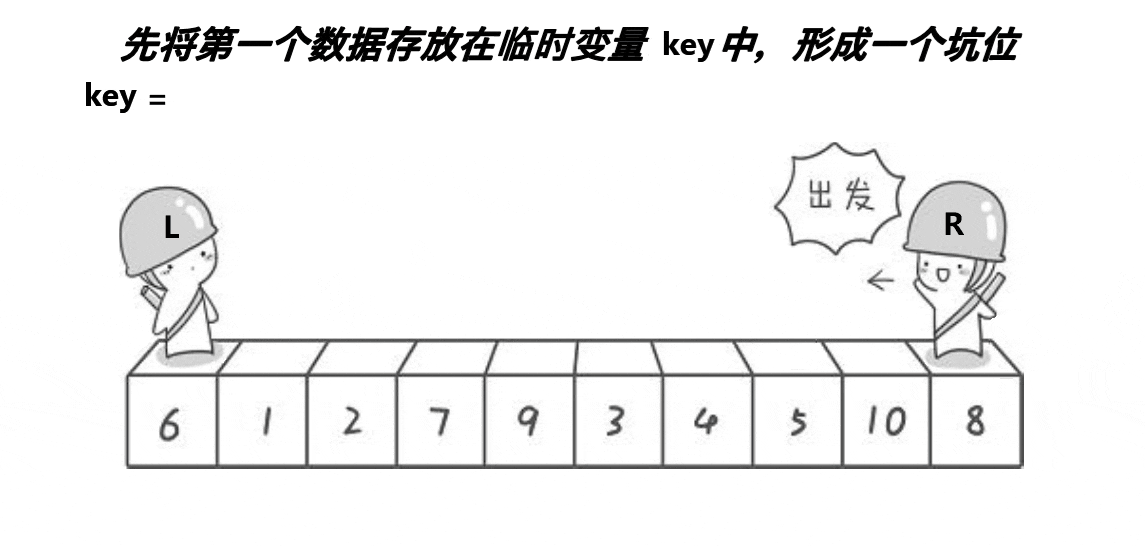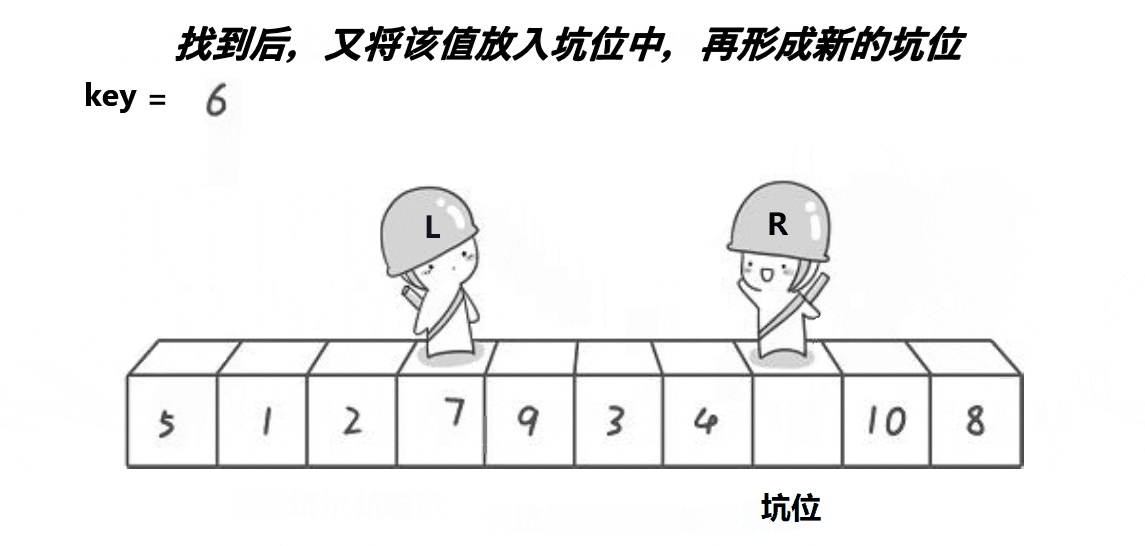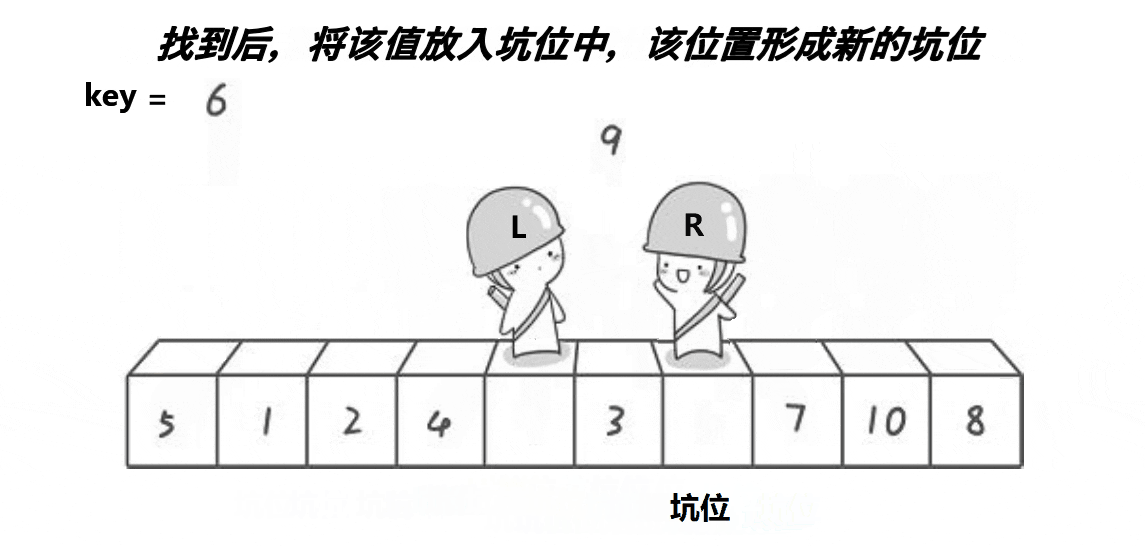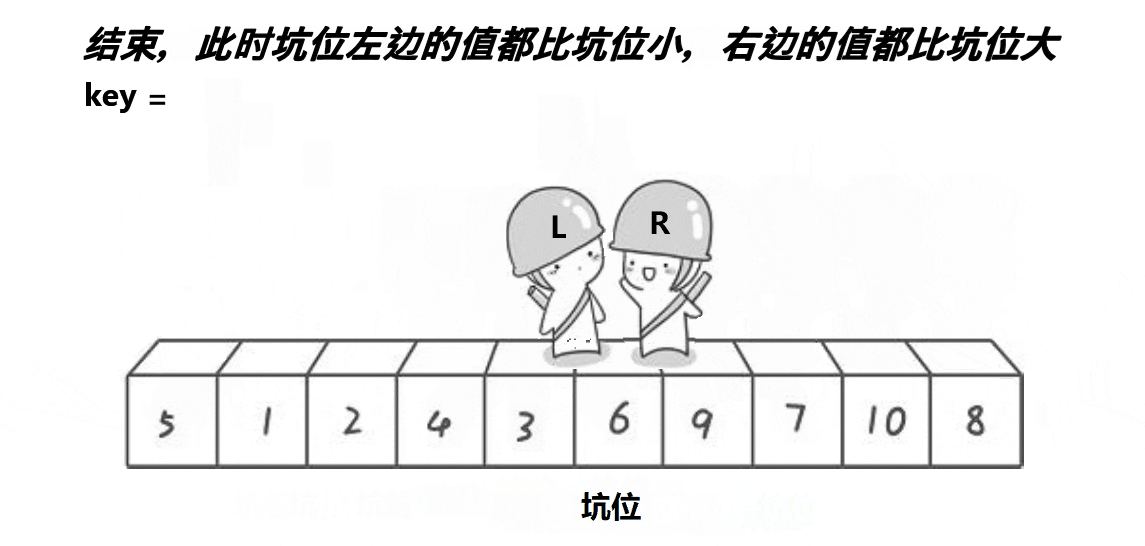
 为了方便讲解，我们先将keyi=left，使得每次key都是最左边的元素。

并用left和right分别标记数组的最左/右端。（左边为key，右边先找，后续讲解原因）。

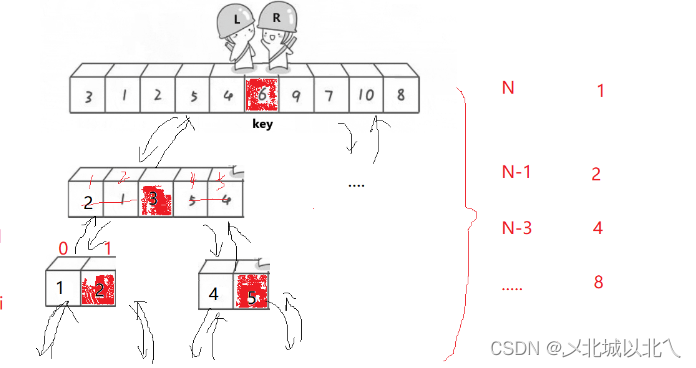
        对于1-10的十个数，我们第一趟快排的目的是将6排到下标为5的位置上，并且保证它左边的数都小于6，右边的数都大于6.（这是为了保证，分别对其左右两端排序后，连接上这个6，整体的数组为升序，从而达到排序目的）。

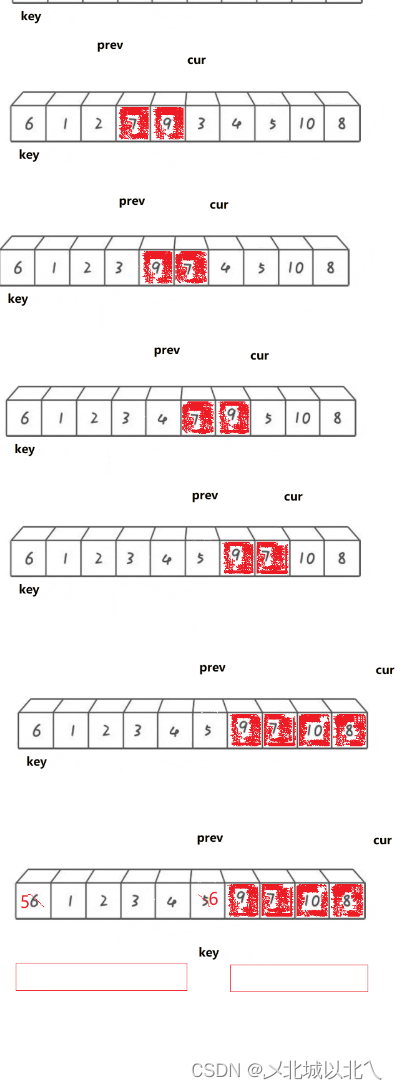
        right从最右端开始找比key==6小的数，找不到就--right，直到用right标记小的这个数。

right找到小后，left开始从左边找比key==6大的数，找不到就++left。只要满足left<right就可以一直找，直到left和right相遇。

        然后将相遇点的数与key交换，此时key就来到了正确的位置。因为刚刚left和right查找并交换的过程，使得比key大的数都到了key左边，而比key小的数也交换到了右边。

void QuickSort(int* arr, int left,int right)
{
	int keyi = left;

	while (left < right)
	{

		//先从右边开始找
		while ((left<right) && arr[right] >= arr[keyi])//右边找小
		{
			--right;
		}
		while ((left<right) && arr[left] <= arr[keyi])//左边找大
		{
			++left;
		}


		Swap(&arr[left], &arr[right]);
	}
	//出来后left == right ，交换它与key
	Swap(&arr[left], &arr[keyi]);
	keyi = left;//此时keyi在正确的位置


}

当然，注意一点，最后交换了重合位置与key的值之后，还要让keyi=left，更新一下keyi的位置，便于后续递归。

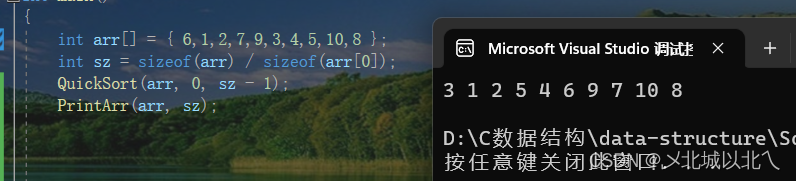
观察打印后的结果，6排到了正确的位置，比它小的在它左边，比它大的在它右边。 

递归实现key左右两端快排

我们实现快排有3个参数，一个是指向数组第一个元素的指针，另外是下标left和right。

为了对key左右分别递归快排，arr数组不变，需要记录左右两部分各自的left和right位置。

但是因为left和right在排序过程中会改变，因此可以定义begin和end来保存起始和结束的位置。

然后对 [begin,keyi-1] 和 [keyi+1,end]分别递归进行快排。

 当排序区间[left,right]只有一个元素或没有元素时返回。即left>=right时。

void QuickSort(int* arr, int left,int right)
{
	if (left >= right)
	{
		return;
	}

	int begin = left;
	int end = right;

	int keyi = left;

	while (left < right)
	{

		//先从右边开始找
		while ((left<right) && arr[right] >= arr[keyi])//右边找小
		{
			--right;
		}
		while ((left<right) && arr[left] <= arr[keyi])//左边找大
		{
			++left;
		}

		Swap(&arr[left], &arr[right]);
	}
	//出来后left == right ，交换它与key
	Swap(&arr[left], &arr[keyi]);
	keyi = left;//此时keyi在正确的位置

	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi + 1, end);

}

缺陷：

有一个要注意的点，加入数组中不止一个值为6，当right找小时不能停下，否则当left也为6时，就会产生2个6一直交换，66...66...66....  导致死循环，因此必须严格找小/大。

还有一件事，right找小时不能闷着头找，一直--，同时还要保证left<right。

时间复杂度分析 

最优情况：O(NlogN)

假设每次选到的left位置的key都是这个数组中大小处于中间位置的数据，那么可以将它左右两边的n-1个数据平均分成两组，然后递归快排。

这两边的元素若仍满足，可以再对n-3个分成4组。（此时又排好了2个）

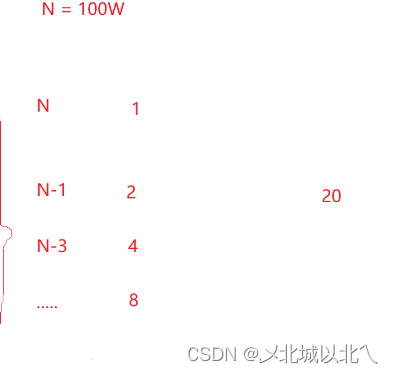
 对于100W个数据，可以分出来约20层，每层有2^n组，每组可以额外少排2^(n-1)次方个数，当然还要加上之前的，大约是2^n个。

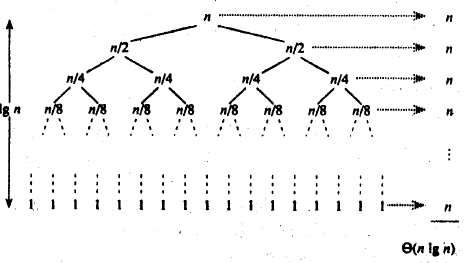
换句话说，对于快排整体来说，总共要递归20层，每层大概有n个（实际上比n小一点）元素，因此其时间复杂度可认为是O(NlogN)

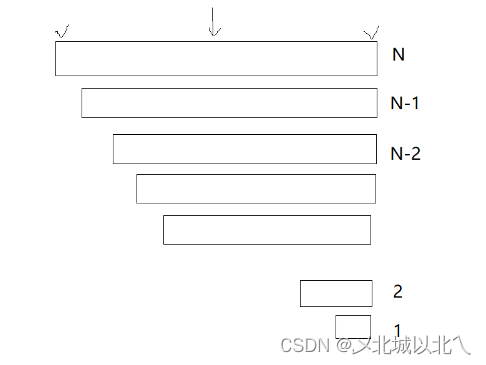
最坏情况：O(N^2)

当数组已经是有序（不论升序还是降序），此时keyi标记的数据是数组中的max或min，在进行下一层递归时，一侧为0个元素，另外一侧为n-1个元素，也就是说，要递归N层！

首先，N足够大时，递归N层会导致栈溢出，程序直接崩掉。

然后，这个快速排序就退化成了冒泡排序 ，第一层遍历N个，第二层N-1个，……直到最后1个。

为等差数列，计算后时间复杂度为O(N)。

缺点分析及优化方法：

一个是代码实现上需要注意的几点，是否出现死循环/越界，还有一个优化点就是有序数组退化的问题，时间复杂度大，且可能导致栈溢出。

这些问题的本质是因为我们默认keyi的位置是left，当知到默认为left时，我们当然可以通过有序数组的特殊例子来“推翻”快速排序。下面给出2中优化方法。

随机数优化法：

随机数优化方法就是keyi的位置不固定为left，而是[left,right]中的任一位置，这样就可以嘴大尺度避免有序的特殊情况，（当然顺序的情况也会出现，但概率极低，只有数组有序，且随机到left或right时才会出现）。

这里可以改为   keyi = left +rand() %(right-left+1),得到[0,right-left],再加上left，范围是[left,right]

void QuickSort(int* arr, int left,int right)
{
	if (left >= right)
	{
		return;
	}

	int begin = left;
	int end = right;

	  //随机数法，得到一个下标
	int rand = Qsortrand(arr, left, right);
	Swap(&arr[left], &arr[rand]);
	

	int keyi = left;

	while (left < right)
	{

		//先从右边开始找
		while ((left<right) && arr[right] >= arr[keyi])//右边找小
		{
			--right;
		}
		while ((left<right) && arr[left] <= arr[keyi])//左边找大
		{
			++left;
		}

		Swap(&arr[left], &arr[right]);
	}
	//出来后left == right ，交换它与key
	Swap(&arr[left], &arr[keyi]);
	keyi = left;//此时keyi在正确的位置

	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi + 1, end);

}

用区间的开始left，加上范围在区间的差（right-left）内的随机数，使得随机数落在区间范围内。

得到随机数的下标后，它的值可能是数组中的任意大小，因此便于后面的递归排序。

交换 left 与 rand两个值，keyi仍然指向left，但此时arr[left]已经是随机的了

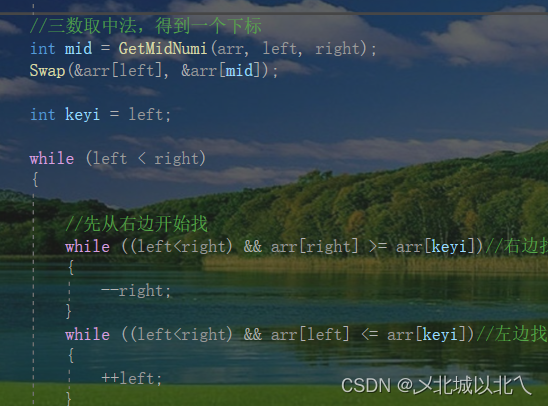
三数取中优化法：

因为随机数法还是有可能选到最大/最小的数据的，因此又有人提出来三数取中法。

即在arr[left]/arr[right]/arr[mid]中选出中间大小的数，既保证了随机选择，又避免了取到最大/最小，进一步提升了效率。

//三数取中法优化快排
int GetMidNumi(int* arr, int left, int right)
{
	int mid = (left + right) / 2;

	//  先取出 最左端、最右端、中间的数据
	//  比较出大小后返回的是下标
	if (arr[left] > arr[right])
	{
		if (arr[mid] < arr[right])
		{
			return right;
		}
		else if (arr[left] > arr[mid])
		{
			return mid;
		}
		else
		{
			return left;
		}
	}
	else
	{
		if (arr[left] > arr[mid])
		{
			return left;
		}
		else if (arr[right] > arr[mid])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

 返回的是3个数中  中间大小的下标。

 接收后，同样将left与这个中间数的值交换，这样left指向的值就是随机的，且不为最大/最小。

经过上面的优化，避免了最坏情况，快排的时间复杂度可认为是O(NlogN)。

左key右先走的解释：

1、普通情况：此时，right找小，找到后停下，left找大，找到后停下，互相交换，此时left和right没有相遇，一直重复上述过程。

2、左遇右：此时右边已经停下，则arr[right]<key是成立的，左边一直找大，没有找到，直到与right相遇，此时二者都指向一个比key小的数。

3、右遇左：上一次普通情况交换数据后，arr[left]<key,此时右边找小，没找到，直到与left重合，此时二者都指向一个比key小的值。（这里有一种特殊情况，如果是升序，右边也找不到小，直到与左边重合，此时都指向第一个元素）。

找到key该在的位置后，交换arr[keyi]与这个位置的值即可排好key。

如果是左key左先走，在一个比key大的位置停留，若此时右边再走，与left重合，二者指向的值比key大，再交换就发生错误了。

挖坑法：

整体思想上与Hoare方法类似，效率也差不多，但可能比较好理解一点。

 先将arr[left]拿出来保存在tmp中，此时left的位置可以看作是一个坑，用hole标记，之后的操作就是不断的填坑，挖坑，再填坑。

        因为坑在左边，所以从右边开始找小，找到后arr[hole]=arr[right],将右边这个小于key的值填入坑中，然后hole=right，更新坑的位置，然后坑就在右边了。

之后不断重复，因为left和right一定有一个与hole重合，所以left==right时，hole也在相同的位置。因此arr[hole]=tmp最终把tmp的保存的值填入坑中即可。然后递归hole两侧进行后续快排。

//  挖坑法快排
void QsortHole(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	int begin = left;
	int end = right;

	int mid = GetMidNumi(arr, left, right);
	Swap(&arr[mid], &arr[left]);
	int tmp = arr[left];
	int hole = left;

	while (left < right)
	{
		//  右边找小
		while (left < right && arr[right] >= tmp)
		{
			right--;
		}
		//  右边填左边的坑
		arr[hole] = arr[right];
		hole = right;

		//  左边找大
		while (left < right && arr[left] < tmp)
		{
			++left;
		}
		//   左边填右边的坑
		arr[hole] = arr[left];
		hole = left;
		
	}
	arr[hole] = tmp;

	QsortHole(arr, begin, hole - 1);
	QsortHole(arr, hole + 1, end);

}

要注意的是一开始要用tmp保存值，填坑过程为赋值，并且hole也要更新。

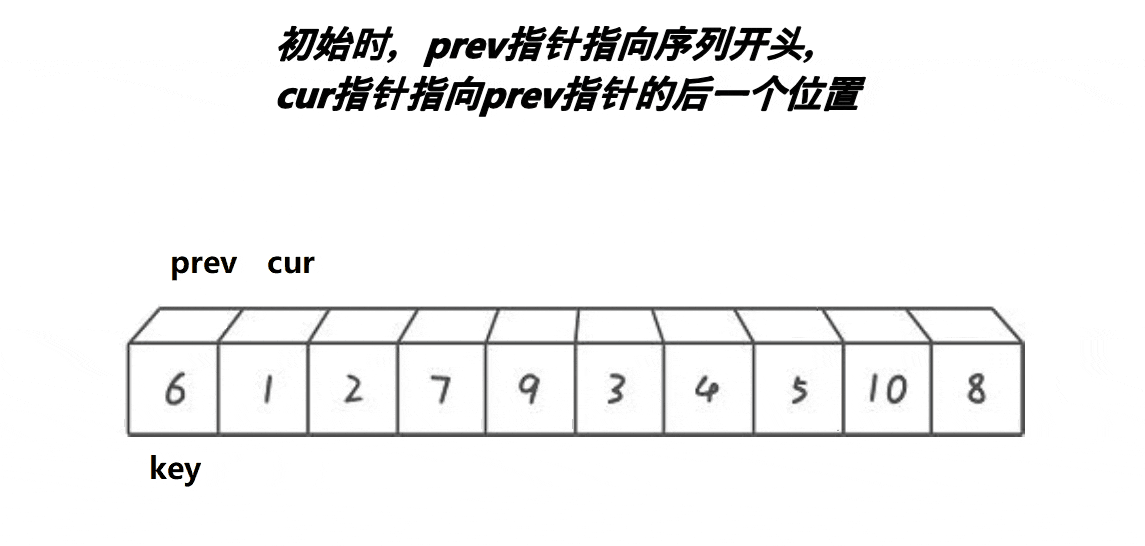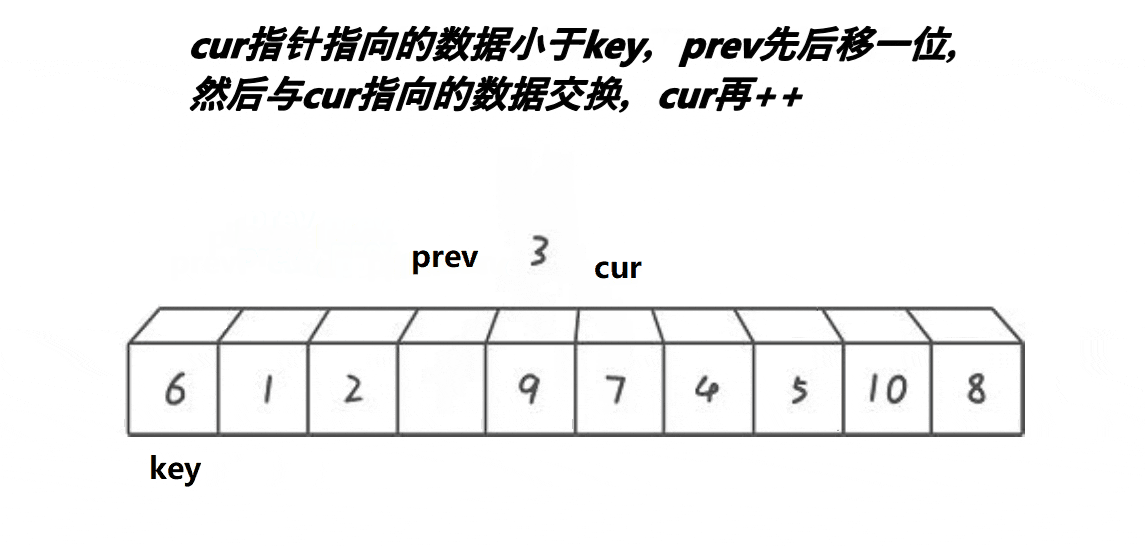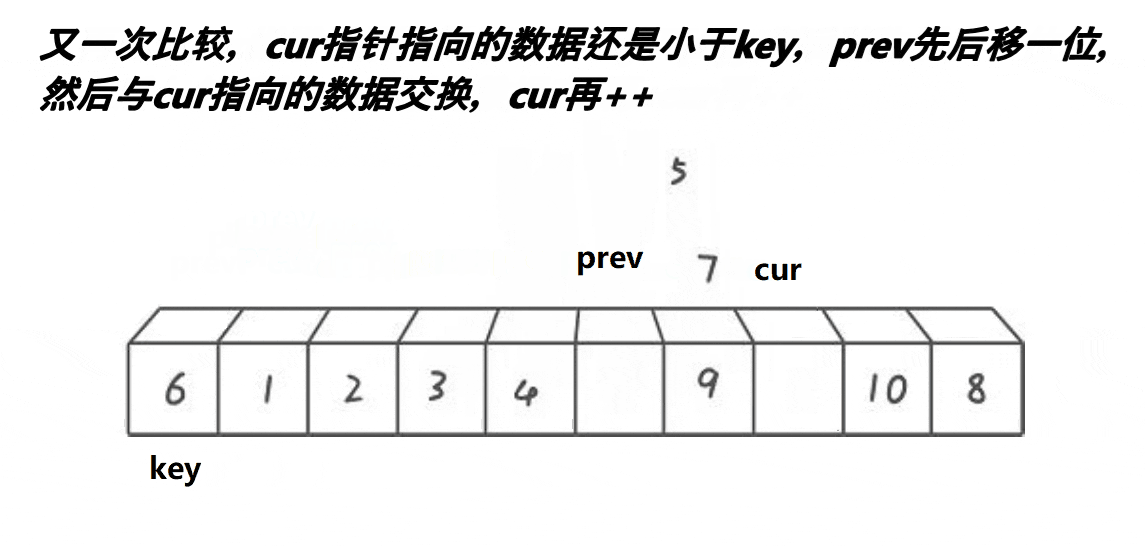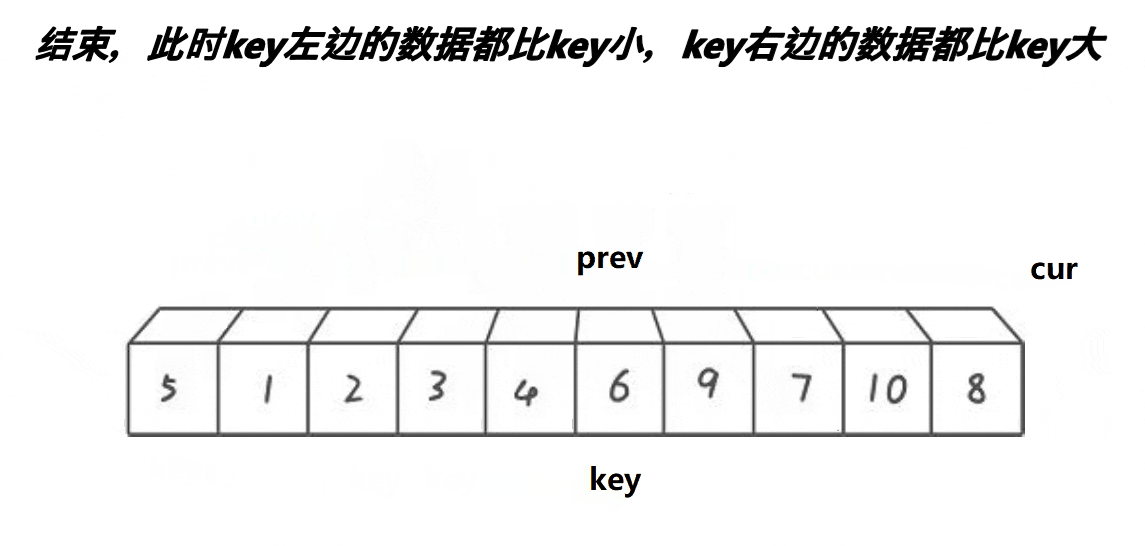
快慢指针（下标）法：

 利用prev、cur两个数组下标，也可看作是指针，二者本质相同。

起始状态，prev和key都指向最左边的元素，cur指向下标为1的。

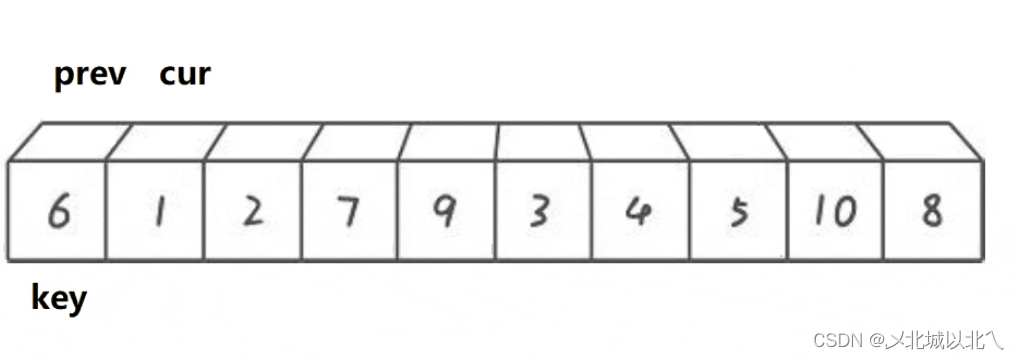
然后先用cur来遍历整个数组找小，如果arr[cur]>=key,则该位置较大，不用交换++cur；如果arr[cur]<key,该位置较小，需要交换。

先++prev，意义是要调整的前面的，较小的数据数+1，因此prev要先+1.然后Swap(&arr[prev],&arr[cur])。

重复上述过程。

通过观察我们可以发现，prev与cur之间如果存在数据，那么这些数据都是大于key时cur多走的。

 当cur>key时，cur就遍历完了整个数组，将所有小于key的值都交给了arr[prev]，此时prev及其左侧的数均<key(起始位置除外)，最后再交换一下起始位置和当前prev的位置。

最后再以prev为分隔，分别递归两侧，进行后续快排。

//  快慢指针法快排
void QSortByPtrs(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	int begin = left;
	int end = right;

	int midi = GetMidNumi(arr, left, right);
	printf("%d\n", arr[midi]);
	Swap(&arr[left], &arr[midi]);
	int key = arr[left];

	int cur = left + 1;
	int prev = left;
	while (cur <= right)
	{
		while (cur <= right && arr[cur] >= key)
		{
			++cur;
		}
		if (cur <= right && arr[cur] < key)
		{
			++prev;
			if (prev != cur)
				Swap(&arr[prev], &arr[cur]);

			++cur;
		}
	}
	//cur遍历完后，prev指向的位置就是key的最终位置
	Swap(&arr[prev], &arr[begin]);

	//递归实现后续快排
	QSortByPtrs(arr, begin, prev - 1);
	QSortByPtrs(arr, prev+1, end);
}

要注意的是cur和left不能只是1和0，而是要根据left去取值，否则对右边的元素递归会产生错误。

++cur前保证cur<=right,防止越界访问。

最后将begin位置与prev交换，完成一趟快排，然后递归实现后续快排。

递归过程封装：

本文讲了Hoare、挖坑法、快慢指针法三种递归方法完成快速排序，它们的递归过程是相同的，可以将递归结束条件和后续递归过程封装起来，然后在中间调用3种方法的函数，使逻辑更清晰。

 封装中只写结束条件和递归过程。并用一个keyi接收之前3种方法排序后key的下标位置。

1、Hoare方法返回keyi的位置。

2、挖坑法返回最终坑的位置。

3、快慢指针法返回prev的位置。

返回排好的那个数的位置后，再用left，keyi，right进行递归，从而完成快排的递归封装。

目录

快速排序介绍：

Hoare方法实现

递归实现key左右两端快排

缺陷：

时间复杂度分析 

最优情况：O(NlogN)

最坏情况：O(N^2)

缺点分析及优化方法：

随机数优化法：

三数取中优化法：

左key右先走的解释：

挖坑法：

快慢指针（下标）法：

递归过程封装：