【数据结构】十种排序算法---C语言实现

十种排序算法

冒泡
选择
插入
希尔
快速
归并
堆
计数
桶
基数

在这里插入图片描述
文章中动图来源：C语言十大经典排序算法

排序算法
排序算法的稳定性：
稳定排序：排序过程中关键字相同的元素的相对次序不变
不稳定排序：排序过程中关键字相同的元素的相对次序发生变化

（堆，快，选，希）—四种不稳定排序

要求在整个排序过程中，而不是排序结束后

内部排序：所有数据在内存
外部排序：部分数据在内存，部分数据在外存，涉及到内外存的交换

基本方法：

插入方法（简单插入排序，希尔排序）
交换方法（冒泡，快排）
选择方法（选择排序）
归并方法
基数方法

评价指标：比较/移动/交换元素的次数

冒泡

数据左右进行比较，把最大的数一直交换到最后，特点是该算法对数据的有序性敏感，在排序过程中发现有序可以立即停止排序，如果待排序的数据基本有序，则冒泡的效率非常高

冒泡排序的写法也比较多，终极思想就是从头到尾遍历，然后相邻两个数比较，把较大的数放后面

时间复杂度：最优O(N) 平均：O(N^2)
稳定的
在这里插入图片描述

//冒泡排序 --经典版
void bubble_sort(TYPE *arr,size_t len){
	for(int i = 0;i<len-1;i++){
        for(int j =0;j<len-i-1;j++){
            if(arr[j]>arr[j+1])
                swap(arr[j],arr[j+1]);
        }
    }
}
//升级版--加一个标志位，如果已经有序，不再继续排序了
void bubble_sort_plus(TYPE *arr,size_t len){
    bool flag = true;
    for(int i = len-1;i>0 && flag;i--){
        flag = false;
        for(int j = 0;j<i;j++){
            if(arr[j]>arr[j+1]){
                swap(arr[j],arr[j+1]);
                flag = true;
            }
        }
    }
}

选择

假定最开始的位置是最小值并记录下标min，然后与后面的数据比较，如果有比min为下标的数据还要小，则更新min，最后判断如果min的值发生了改变，则交换min位置的数据与最开始位置的数据
虽然选择排序的时间复杂度较高，但是数据交换次数少，因此实际运行速度并不慢
是冒泡排序的变种，但是没有对数据有序性敏感，数据混乱情况下比冒泡快
时间复杂度：O(N^2)
不稳定的 (10 10 1)
注意：算法的时间复杂度并不能代表算法的实际时间，有时候时间复杂度高的反而速度更快
在这里插入图片描述

//选择排序  不稳定  O(n^2)
//在未排序的序列中找到最小元素，与起始位置互换
//在剩余元素中继续找最小元素，放在已排序序列的末尾
void select_sort(TYPE *arr,size_t len){
    for(int i = 0;i<len-1;i++){
        int min = i; //假设起始位置为最小值，并记录下标
        for(int j = i+1;j<len;j++){
            if(arr[j] < arr[min]) min = j;
        }
        if(i != min) swap(arr[i],arr[min]);
    }
}

插入

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5

时间复杂度：O(N^2)
稳定的

//直接插入排序
void insert_sort(TYPE *arr,size_t len){
	for(int i = 1,j=0;i<len;i++){
        int val = arr[i];
        //从已排序的序列末尾从右往左比较，所有比val的数据往后移
        for(j = i;j>0 && arr[j-1]>val;j--){
            arr[j] = arr[j-1];
        }
       //如果val比已排序的最大值还要大，那么循环没有执行，i仍然等于j
       //如果循环执行了，那么把val赋值给arr[j]
       //由于循环最后一步是j--，所以arr[j]就是合适的位置
        if(i != j) arr[j] = val;
    }
}

希尔

是插入排序的增强版，由于插入排序数据移动的速度比较慢，所以在此基础上增加了增量的概念，从而提高排序的速度
注意：如果数据原本相对有序，那么希尔执行次数比插入排序还要多；对于数据大多数是倒序的情况，希尔更加擅长
时间复杂度：O(N^(1.3~2))
不稳定
在这里插入图片描述

//希尔排序 --插入排序的plus版
void shell_sort(TYPE *arr,size_t len){
    //第一层：划分步长，每次都是上一次的一半，最后一次的步长为1
	for(int k = len/2; k>0; k/=2){
        //第二层：对下标差为步长整数倍的部分进行插入排序
        for(int i = k,j=0;i<len;i++){
            int val = arr[i];
            //注意这里j每次移动k个位置
            for(j=i;j-k>0 && arr[j-k]>val;j-=k){
                arr[j] = arr[j-k];
            }
            if(i ！= j) arr[j] = val;
        }
    }
}

快速

找到一个标杆p，备份标杆p的值val，一面从左找比val大的数据，找到后赋值给p，更新标杆p的位置到左标杆，然后从右边找比val小的数，找到后也赋值给p，同样更新p到右标杆，反复执行直到左右标杆相与停止，最后把val赋值回p的位置，最终会形成p左边的数都比它小，右边的数都比它大；然后再按照同样的方式对左右两边进行快排，最后全部有序
快速排序的综合性能最高，因此叫做快速排序，笔试面试考最多！！！
时间复杂度：O(NlogN)
不稳定
优化思路：选择合适的标杆
三路划分快速排序，随机化快速排序（随机化选择基准，更好的避免最坏情况的性能）
在这里插入图片描述

void _quick_sort(TYPE *arr,int left,int right){
	if(left >= right) return;
    int l = left,r = right;
    int k = (left+right)/2;//优化方向1：用随机值
    TYPE cur = arr[k];
    while(l < r){
        while(l<k && arr[l] <= cur) l++;
        if(l < k){
            swap(arr[l],arr[k]);
            k = l;
        }
        while(r > k && arr[r] >= cur) r--;
        if(r > k){
            swap(arr[r],arr[k]);
            k = r;
        }
    }
    arr[k] = cur;
    if(k-l > 1) _quick_sort(arr,l,k-1);
    if(r-k > 1) _quick_sort(arr,k+1,r);
}
void quick_sort(TYPE *arr,size_t len){
    _quick_sort(arr,0,len-1);
}

归并

先把一组待排序的数据拆分成单独的个体，存放到临时空间中，然后两两比较合并，全部合并完成后再从临时空间中拷贝给原内存
由于使用额外的内存空间避免了数据交换的耗时，是一种典型的以空间换时间的算法
时间复杂度：O(NlogN)
稳定
在这里插入图片描述

//归并排序 --递归版
//合并
void merge(TYPE *arr,TYPE *temp,int l,int p,int r){
	//l左部分最左，p左部分最右，p+1右部分最左，r右部分最右
	//认为左右部分各自有序
	if(arr[p] < arr[p+1]) return;
	int k = l,i = l,j = p+1;
	while(i<=p && j<=r){
		//左右部分从左开始比较，谁小就放入temp
		if(arr[i] <= arr[j]){
			temp[k++] = arr[i++];
		}else{
			temp[k++] = arr[j++];
		}
	}
	//比较完后，把还没参与比较的数据放到temp末尾
	while(i<=p) temp[k++] = arr[i++];
	while(j<=r) temp[k++] = arr[j++];
	memcpy(arr+l,temp+l,sizeof(TYPE)*(r-l+1));
}
//拆分
void _merger_sort(TYPE *arr,TYPE *temp,int l,int r){
	if(l >= r) return;
	int p = (l+r)/2;
	_merger_sort(arr,temp,1,p);
	_merger_sort(arr,temp,p+1,r);
	merge(arr,temp,0,p,r);
}
//调用
void merge_sort(TYPE *arr,size_t len){
	TYPE *temp = malloc(sizeof(TYPE)*len);
	_merger_sort(arr,temp,0,len-1);
	free(temp);
	show_arr(arr,len);
	printf("%s \n",__func__);
}

//归并排序 ---非递归
void merger_sort(TYPE *arr,size_t len){
	TYPE *temp = malloc(sizeof(TYPE)*len);
	TYPE *src = arr,*dest = temp;
	//s是间隔元素个数，从1开始，每次翻倍
	for(int s = 1;s<len;s*=2){
		//l是左部分最左，合并一次后，l+=s*2是下一次左部分最左
		for(int l = 0;l<len;l+=s*2){
			//r是右部分最右+1
			int r = (l+s*2<len)?l+s*2:len;
			//p是右部分最左
			int p = (l+s<len)?l+s:len;
			int k = l,i=l,j=p;
			while(i<p && j<r){
				if(src[i] < src[j]){
					dest[k++] = src[i++];
				}else{
					dest[k++] = src[j++];
				}

			}
			while(i<p) dest[k++] = src[i++];
			while(j<r) dest[k++] = src[j++];
		}	
		swap(dest,src);
	}
	if(src != arr) 
		memcpy(arr,src,sizeof(TYPE)*len);
	free(temp);
	show_arr(arr,len);
	printf("%s \n",__func__);
}

堆

把数据当做当做完全二叉树看待，然后把树调整成大顶堆，然后把堆顶数据交换到末尾，然后数量–，然后重新调整回大顶堆，重复操作，直到数量为1时结束，既可以循环实现也可以递归实现(参考 heap.c)
时间复杂度：O(n*log n)
不稳定

//堆排序  非递归
void sort_heap(TYPE *arr,size_t len){
	//把数组调整为堆
	for(int i = 1;i<=len;i++){
		int j = i;
		while(j > 1){
			if(arr[j/2-1] < arr[j-1]){
				swap(arr[j/2-1],arr[j-1]);
			}
			j = j/2;
		}
	}
	//删除堆顶，直到堆为空
	int num = len;
	while(num > 1){
		swap(arr[0],arr[num-1]);
		num--;
		int i = 1;
		while(i-1 < num){
			if(2*i <num){
				if(arr[2*i] >= arr[2*i-1] && arr[2*i] > arr[i-1]){
					swap(arr[2*i],arr[i-1]);
					i = 2*i+1;
				}
				else if(arr[2*i-1] > arr[2*i] && arr[2*i-1] > arr[i-1]){
					swap(arr[2*i-1],arr[i-1]);
					i = 2*i;
				}
				else{
					break;
				}
			}
			else if(2*i-1 < num){
				if(arr[2*i-1] > arr[i-1]){
					swap(arr[2*i-1],arr[i-1]);
					i = i*2;
				}else{
					break;
				}
			}else{
				break;
			}
		}
	}
	show_arr(arr,len);
	printf("%s \n",__func__);
}

计数

找出数据中的最大值和最小值，并创建哈希表，把数据-最小值作为数组的下标访问哈希表并标记数量，标记完后，遍历哈希表，当表中的值大于0，把下标+最小值还原数据依次放回数组中，是一种典型的以空间换时间的算法
该排序算法理论上速度非常快，它不是基于比较的算法，在一定范围内整数排序时快于任意的一种比较排序算法，但是有很大的局限性：适合排序整形数据，而且数据的范围差别不宜过大，否则会非常浪费内存反而慢于比较的排序，如果数据越平均、重复数越多，性价比越高
时间复杂度：Ο(N+k)（其中k是整数的范围）
稳定的
在这里插入图片描述

//计数排序
void count_sort(TYPE *arr,size_t len){
	TYPE min = arr[0],max = arr[len-1];
	for(int i = 0;i<len;i++){
		if(arr[i] < min) min = arr[i];
		if(arr[i] > max) max = arr[i];
	}
	TYPE *temp = calloc(sizeof(TYPE),max-min+1);
	for(int i = 0;i<len;i++){
		temp[arr[i]-min]++;
	}
	for(int j = 0,i = 0;i<=max-min;i++){
		while(temp[i]--){
			arr[j++] = i+min;
		}
	}
	free(temp);
	show_arr(arr,len);
	printf("%s\n",__func__);
}

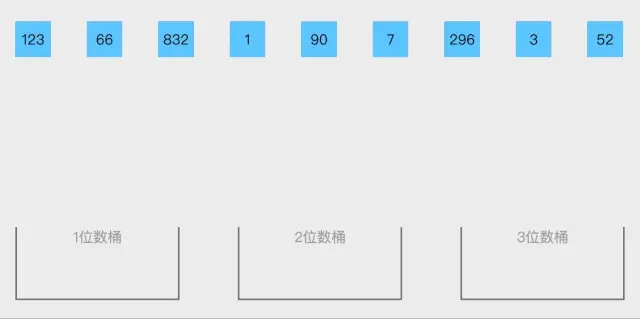
桶

根据数据的值存储到不同的桶中，然后再调用其它的排序算法，度桶中的数据进行排序，然后再从桶中依次拷贝回数组中，从而降低排序的规模以此提高排序的速度，是一种典型的以空间换时间的算法
缺点：如何分桶、桶范围多大，这些都需要对数据有一定的了解
时间复杂度：Ο(N+k)
桶排序的稳定性取决于桶内排序使用的算法
在这里插入图片描述

//桶排序
void _bucket_sort(TYPE *arr,size_t len,int cnt,TYPE range){
	//申请桶的内存
	//bucket指向桶的开头，bucketend指向桶的末尾
	TYPE *bucket[cnt],*bucketend[cnt];
	for(int i = 0;i<cnt;i++){
		//数据可能全部在一个桶
		bucket[i] = malloc(sizeof(TYPE)*len);
		//开始时，起始位置，末尾都指向开头
		bucketend[i] = bucket[i];
	}
	//把所有数据按照桶设的范围放入相应的桶中
	for(int i = 0;i<len;i++){
		for(int j = 0;j<cnt;j++){
			if(range *j <= arr[i] && range*(j+1) > arr[i]){
				*(bucketend[j]) = arr[i];
				bucketend[j]++;
			}
		}
	}
	//让每个桶的数据排序，最后分别存入arr中
	for(int i = 0;i<cnt;i++){
		//计算每个桶中元素数量
		int size = bucketend[i]-bucket[i];
		//如果有元素，才需要使用别的排序方法进行排序
		if(size > 1){
			count_sort(bucket[i],size);  //调用计数排序
		}
		//把桶按照先后顺序存入arr
		memcpy(arr,bucket[i],sizeof(TYPE)*size);
		arr += size;
	}
}

void bucket_sort(TYPE *arr,size_t len){
	//4个桶 桶的范围10
	_bucket_sort(arr,len,4,10);	
	show_arr(arr,len);
	printf("%s\n",__func__);
}

基数

是桶排序的具体实现，首先创建10个队列(链式队列)，然后逆序计算出数据的个、十、百…位数，然后入到对应的队列中，结束后依次从队列中出队回数组中，数据下一位继续入队，依次循环，最大值的位数就是循环次数
缺点：只适合排序正整数数据，又要准备队列
时间复杂度：Ο(N+k)
稳定的
在这里插入图片描述

//基数排序
void radix_sort(TYPE *arr,size_t len){
	ListQueue *queue[10] = {};
	for(int i = 0;i<10;i++){
		queue[i] = create_list_queue(10);
	}
	//循环次数由最大值的位数决定
	TYPE max = arr[0];
	for(int i = 0;i<len;i++){
		if(arr[i]>max){
			max = arr[i];
		}
	}
	//i=1表示个位，i=2表示十位...
	for(int i = 1,k = 1;max/k>0;k*=10,i++){
		int mod = pow(10,i);
		int div = mod / 10;
		for(int j = 0;j<len;j++){
			//获取每位数据 每位的值 如果mod过大，数据的index都是0
			int index = arr[j]%mod/div;
			push_list_queue(queue[index],arr[j]);
		}
		int k = 0;
		for(int j = 0;j<10;j++){
			//把每个队列中的数据按顺序放回arr中
			while(!empty_list_queue(queue[j])){
				arr[k++] = head_list_queue(queue[j]);
				pop_list_queue(queue[j]);
			}
		}
	}
	show_arr(arr,len);
	printf("%s\n",__func__);
}

完整代码文件：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>
#include<math.h>
#include "queue.c"
#define TYPE int
#define LEN 20

#define swap(a,b) {typeof(a) t=a;a=b;b=t;}

typedef void (*SortFP)(TYPE *,size_t);

//遍历输出
void show_arr(TYPE *arr,size_t len){
	for(int i = 0;i<len;printf("%d ",arr[i++]));
	printf("\n");
}

//冒泡排序 稳定 时间复杂度O(n^2)
void bubble_sort(TYPE *arr,size_t len){
	for(int i = 0;i<len;i++){
		for(int j = i;j<len;j++){
			if(arr[i] > arr[j]){
				swap(arr[i],arr[j]);
			}
		}
	}
/*	bool flag = true;
	for(int i = len-1;i>0 && flag;i--){
		//标志位
		flag = false;
		for(int j = 0;j<i;j++){
			if(arr[j] > arr[j+1]){
				swap(arr[j],arr[j+1]);
				flag = true;
			}
		}
	}*/
	printf("%s\n",__func__);
	show_arr(arr,len);
}

//选择排序 不稳定 O(n^2)
//在未排序的序列中找到最小元素，与起始位置互换
//在剩余元素中继续找最小元素，放在已排序列的末尾
void select_sort(TYPE *arr,size_t len){
	for(int i = 0;i<len-1;i++){
		int min = i;
		for(int j = i+1;j<len;j++){
			if(arr[j] < arr[min]) min = j;
		}
		if(i != min) swap(arr[i],arr[min]);
	}
	printf("%s\n",__func__);
	show_arr(arr,len);
}

//(直接)插入排序 稳定 O(n^2)
void insert_sort(TYPE *arr,size_t len){
	for(int i = 1,j=0;i<len;i++){
		int val = arr[i];
		for(j=i;j>0 && arr[j-1]>val;j--){
			arr[j] = arr[j-1];
		}
		if(j != i) arr[j] = val;
	}
	printf("%s\n",__func__);
	show_arr(arr,len);
}

//希尔排序--插入排序的plus版本
//不稳定 时间复杂度O(n^(1.3~2))
void shell_sort(TYPE *arr,size_t len){
	//第一层：划分步长，每次都是上一次的一半
	for(int k = len/2;k>0;k/=2){
		//第二层：对下标差是步长整数倍的部分进行插入排序
		for(int i = k,j=0;i<len;i++){
			int val = arr[i];
			for(j = i;j-k>=0 && arr[j-k]>val;j-=k){
				arr[j] = arr[j-k];
			}
			if(j != i) arr[j] = val;
		}
	}
	printf("%s\n",__func__);
	show_arr(arr,len);
}

//快速排序 不稳定 O(nlogn)
void _quick_sort(TYPE *arr,int left,int right){
	if(left >= right) return;
	int pi = (left+right)/2;
	TYPE pv = arr[pi]; //备份标杆的值
	int l = left,r = right; //备份左右下标
	//左右下标相遇时结束
	
	//测试
	for(int i = left;i<=right;i++){
		if(i == pi) printf("[%d] ",arr[i]);
		else printf("%d ",arr[i]);
	}
	printf("\n");

	while(l < r){
		//在标杆的左边寻找比它大的数据
		while(l<pi && arr[l] <= pv) l++;
		if(l<pi){  //如果没有超出寻找范围，说明找到了
			arr[pi] = arr[l];
			//更新标杆位置
			pi = l;
		}
		//在标杆的右边寻找比它小的数据
		while(pi<r && arr[r] >= pv) r--;
		if(pi<r){
			arr[pi] = arr[r];
			pi = r;
		}
	}
	//还原标杆的值
	arr[pi] = pv;
	if(pi-left > 1) _quick_sort(arr,left,pi-1);
	if(right-pi > 1) _quick_sort(arr,pi+1,right);
}

void fast_sort(TYPE *arr,size_t len){
	_quick_sort(arr,0,len-1);
	printf("%s\n",__func__);
	show_arr(arr,len);
}

//合并
void merge(TYPE *arr,TYPE *temp,int l,int p,int r){
	//l左部分最左，p左部分最右，p+1右部分最左，r右部分最右
	//认为左右部分各自有序
	if(arr[p] < arr[p+1]) return;
	int k = l,i = l,j = p+1;
	while(i<=p && j<=r){
		//左右部分从左开始比较，谁小就放入temp
		if(arr[i] <= arr[j]){
			temp[k++] = arr[i++];
		}else{
			temp[k++] = arr[j++];
		}
	}
	//比较完后，把还没参与比较的数据放到temp末尾
	while(i<=p) temp[k++] = arr[i++];
	while(j<=r) temp[k++] = arr[j++];
	memcpy(arr+l,temp+l,sizeof(TYPE)*(r-l+1));
}
//拆分
void _merger_sort(TYPE *arr,TYPE *temp,int l,int r){
	if(l >= r) return;
	int p = (l+r)/2;
	_merger_sort(arr,temp,1,p);
	_merger_sort(arr,temp,p+1,r);
	merge(arr,temp,0,p,r);
}

//归并排序
void merge_sort(TYPE *arr,size_t len){
	TYPE *temp = malloc(sizeof(TYPE)*len);
	_merger_sort(arr,temp,0,len-1);
	free(temp);
	show_arr(arr,len);
	printf("%s \n",__func__);
}
//归并排序 ---非递归
void merger_sort(TYPE *arr,size_t len){
	TYPE *temp = malloc(sizeof(TYPE)*len);
	TYPE *src = arr,*dest = temp;
	//s是间隔元素个数，从1开始，每次翻倍
	for(int s = 1;s<len;s*=2){
		//l是左部分最左，合并一次后，l+=s*2是下一次左部分最左
		for(int l = 0;l<len;l+=s*2){
			//r是右部分最右+1
			int r = (l+s*2<len)?l+s*2:len;
			//p是右部分最左
			int p = (l+s<len)?l+s:len;
			int k = l,i=l,j=p;
			while(i<p && j<r){
				if(src[i] < src[j]){
					dest[k++] = src[i++];
				}else{
					dest[k++] = src[j++];
				}

			}
			while(i<p) dest[k++] = src[i++];
			while(j<r) dest[k++] = src[j++];
		}	
		swap(dest,src);
	}
	if(src != arr) 
		memcpy(arr,src,sizeof(TYPE)*len);
	free(temp);
	show_arr(arr,len);
	printf("%s \n",__func__);
}

//堆排序  非递归
void sort_heap(TYPE *arr,size_t len){
	//把数组调整为堆
	for(int i = 1;i<=len;i++){
		int j = i;
		while(j > 1){
			if(arr[j/2-1] < arr[j-1]){
				swap(arr[j/2-1],arr[j-1]);
			}
			j = j/2;
		}
	}
	//删除堆顶，直到堆为空
	int num = len;
	while(num > 1){
		swap(arr[0],arr[num-1]);
		num--;
		int i = 1;
		while(i-1 < num){
			if(2*i <num){
				if(arr[2*i] >= arr[2*i-1] && arr[2*i] > arr[i-1]){
					swap(arr[2*i],arr[i-1]);
					i = 2*i+1;
				}
				else if(arr[2*i-1] > arr[2*i] && arr[2*i-1] > arr[i-1]){
					swap(arr[2*i-1],arr[i-1]);
					i = 2*i;
				}
				else{
					break;
				}
			}
			else if(2*i-1 < num){
				if(arr[2*i-1] > arr[i-1]){
					swap(arr[2*i-1],arr[i-1]);
					i = i*2;
				}else{
					break;
				}
			}else{
				break;
			}
		}
	}
	show_arr(arr,len);
	printf("%s \n",__func__);
}

//计数排序
void count_sort(TYPE *arr,size_t len){
	TYPE min = arr[0],max = arr[len-1];
	for(int i = 0;i<len;i++){
		if(arr[i] < min) min = arr[i];
		if(arr[i] > max) max = arr[i];
	}
	TYPE *temp = calloc(sizeof(TYPE),max-min+1);
	for(int i = 0;i<len;i++){
		temp[arr[i]-min]++;
	}
	for(int j = 0,i = 0;i<=max-min;i++){
		while(temp[i]--){
			arr[j++] = i+min;
		}
	}
	free(temp);
	show_arr(arr,len);
	printf("%s\n",__func__);
}

//桶排序
void _bucket_sort(TYPE *arr,size_t len,int cnt,TYPE range){
	//申请桶的内存
	//bucket指向桶的开头，bucketend指向桶的末尾
	TYPE *bucket[cnt],*bucketend[cnt];
	for(int i = 0;i<cnt;i++){
		//数据可能全部在一个桶
		bucket[i] = malloc(sizeof(TYPE)*len);
		//开始时，起始位置，末尾都指向开头
		bucketend[i] = bucket[i];
	}
	//把所有数据按照桶设的范围放入相应的桶中
	for(int i = 0;i<len;i++){
		for(int j = 0;j<cnt;j++){
			if(range *j <= arr[i] && range*(j+1) > arr[i]){
				*(bucketend[j]) = arr[i];
				bucketend[j]++;
			}
		}
	}
	//让每个桶的数据排序，最后分别存入arr中
	for(int i = 0;i<cnt;i++){
		//计算每个桶中元素数量
		int size = bucketend[i]-bucket[i];
		//如果有元素，才需要使用别的排序方法进行排序
		if(size > 1){
			count_sort(bucket[i],size);
		}
		//把桶按照先后顺序存入arr
		memcpy(arr,bucket[i],sizeof(TYPE)*size);
		arr += size;
	}
}

void bucket_sort(TYPE *arr,size_t len){
	//4个桶 桶的范围10
	_bucket_sort(arr,len,4,10);	
	show_arr(arr,len);
	printf("%s\n",__func__);
}

//基数排序
void radix_sort(TYPE *arr,size_t len){
	ListQueue *queue[10] = {};
	for(int i = 0;i<10;i++){
		queue[i] = create_list_queue(10);
	}
	//循环次数由最大值的位数决定
	TYPE max = arr[0];
	for(int i = 0;i<len;i++){
		if(arr[i]>max){
			max = arr[i];
		}
	}
	//i=1表示个位，i=2表示十位...
	for(int i = 1,k = 1;max/k>0;k*=10,i++){
		int mod = pow(10,i);
		int div = mod / 10;
		for(int j = 0;j<len;j++){
			//获取每位数据 每位的值 如果mod过大，数据的index都是0
			int index = arr[j]%mod/div;
			push_list_queue(queue[index],arr[j]);
		}
		int k = 0;
		for(int j = 0;j<10;j++){
			//把每个队列中的数据按顺序放回arr中
			while(!empty_list_queue(queue[j])){
				arr[k++] = head_list_queue(queue[j]);
				pop_list_queue(queue[j]);
			}
		}
	}
	show_arr(arr,len);
	printf("%s\n",__func__);
}


int main(int argc, const char* argv[])
{
	TYPE arr[LEN] = {};
	SortFP sort[] = {bubble_sort,select_sort,insert_sort,shell_sort,fast_sort,merge_sort,merger_sort,sort_heap,count_sort,bucket_sort,radix_sort};
	for(int i = 0;i<sizeof(sort)/sizeof(sort[0]);i++){
		printf("----------------------\n");
		for(int i = 0;i<LEN;i++){
			arr[i] = rand()%40+2;
			printf("%d ",arr[i]);
		}
		printf("\n");
//		show_arr(arr,LEN);
		sort[i](arr,LEN);
	}
	return 0;
}

【数据结构】十种排序算法---C语言实现

十种排序算法

冒泡

选择

插入

希尔

快速

归并

堆

计数

桶

基数

悦读