矩阵论在深度学习中的应用

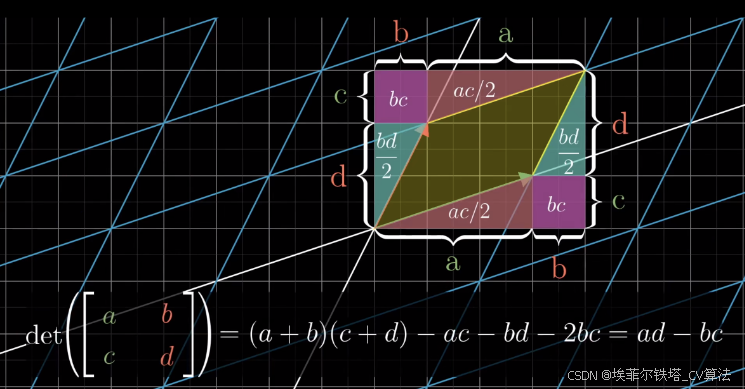
摘要： 本文深入探讨了矩阵论在深度学习领域的广泛应用。首先介绍了深度学习中数据表示和模型结构与矩阵的紧密联系，接着详细阐述了矩阵论在神经网络训练算法优化、卷积神经网络（CNN）、循环神经网络（RNN）及其变体中的关键作用。此外，还分析了矩阵分解技术在模型压缩和加速方面的应用，以及矩阵论在处理深度学习中的大规模数据和高维特征方面的优势。通过这些讨论，展现了矩阵论作为深度学习核心数学工具的重要性，为进一步理解和改进深度学习算法提供了理论依据和实践指导。

一、引言

深度学习作为当今人工智能领域最具影响力的技术之一，在图像识别、自然语言处理、语音识别等众多领域取得了显著的成果。深度学习模型通常包含大量的参数和复杂的计算，而这些计算和参数的表示与处理都离不开矩阵论的支持。矩阵论为深度学习算法的设计、分析和优化提供了坚实的数学基础，理解矩阵论在深度学习中的应用对于深入研究和改进深度学习技术具有至关重要的意义。

二、深度学习中的矩阵表示

（一）数据的矩阵表示

在深度学习中，数据通常以矩阵形式进行表示。例如，在图像数据处理中，一幅彩色图像可以看作是一个三维矩阵，其维度分别表示图像的高度、宽度和颜色通道。对于一批图像数据，可以将其表示为一个四维张量，其中额外的维度表示图像的数量。类似地，在自然语言处理中，文本数据可以通过词向量表示转化为矩阵形式，如一个句子可以表示为一个词向量组成的矩阵，其中每行代表一个词的向量表示。

（二）模型参数的矩阵表示

深度学习模型由大量的参数组成，这些参数在神经网络中以矩阵形式存在。例如，全连接神经网络的每一层权重可以表示为一个矩阵，其行数和列数分别对应输入和输出神经元的数量。对于卷积神经网络，卷积核也是以矩阵形式存在，通过与输入数据的卷积运算实现特征提取。这种矩阵表示形式使得模型参数的计算和更新可以利用高效的矩阵运算来实现。

三、矩阵论在神经网络训练算法中的应用

（一）梯度下降与矩阵运算

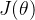
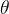
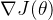
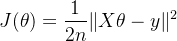
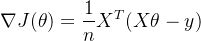
梯度下降是神经网络训练中最常用的优化算法之一。在计算损失函数关于模型参数的梯度时，需要对大量的数据进行计算。以批量梯度下降为例，假设损失函数为 $J(\theta)$ ，模型参数为 $\theta$ ，训练数据为一个矩阵X ，对应的标签为一个向量y 。在计算梯度 $\nabla J(\theta)$ 时，涉及到对损失函数关于每个参数的偏导数计算，这些计算可以通过矩阵运算高效地实现。例如，对于线性回归模型 $y = X\theta + \epsilon$ ，其损失函数 $J(\theta)=\frac{1}{2n}\|X\theta - y\|^2$ ，梯度 $\nabla J(\theta)=\frac{1}{n}X^T(X\theta - y)$ ，这里的 $X^T$ 表示X 的转置矩阵，通过矩阵乘法和加法运算可以快速计算出梯度，从而更新模型参数。

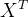
（二）牛顿法及其变体与海森矩阵

牛顿法是一种基于二阶导数信息的优化算法。在深度学习中，牛顿法及其变体（如拟牛顿法）可用于加速训练过程。牛顿法的更新公式为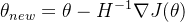 $\theta_{new}=\theta - H^{-1}\nabla J(\theta)$ ，其中 $H$ 是海森矩阵，即损失函数的二阶导数矩阵。计算海森矩阵及其逆矩阵在高维情况下计算量巨大，但通过一些近似方法可以利用矩阵论知识来降低计算复杂度。例如，拟牛顿法中的 BFGS 算法通过使用一个近似的海森矩阵B ，并通过迭代更新 B 的方式来逼近真实的海森矩阵，其更新过程涉及到矩阵的乘法、加法和求逆等运算，这些运算都是基于矩阵论的基本操作，从而在一定程度上利用了二阶信息来加速训练。

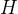
（三）随机梯度下降（SGD）及其改进算法中的矩阵扰动

随机梯度下降是一种在深度学习中广泛应用的优化算法，它每次随机选择一个样本或一小批样本进行梯度计算和参数更新。在 SGD 的一些改进算法中，如 Adagrad、Adadelta、RMSProp 和 Adam 等，会对梯度进行一些基于矩阵论的处理。例如，Adagrad 算法会根据每个参数的历史梯度平方和来调整学习率，这个历史梯度平方和可以看作是一个对角矩阵，其对角元素对应每个参数的梯度平方累积值。在更新参数时，通过将当前梯度除以这个对角矩阵的平方根来调整学习率，这种基于矩阵元素操作的方法可以使学习率自适应地调整，提高训练效率。

四、矩阵论在卷积神经网络（CNN）中的应用

（一）卷积运算的矩阵表示与优化

卷积是卷积神经网络的核心操作。将卷积运算表示为矩阵乘法可以利用高效的矩阵计算库来加速计算。例如，可以通过将输入图像和卷积核进行适当的重塑和填充零，将卷积操作转化为矩阵乘法。设输入图像矩阵为I ，卷积核矩阵为K ，通过特定的变换可以得到新的矩阵I' 和，K'使得卷积结果可以通过I'K' 的矩阵乘法形式得到。这种矩阵表示方法不仅提高了计算速度，还可以方便地利用 GPU 等并行计算设备进行加速。

（二）池化操作的矩阵分析

池化操作是 CNN 中用于减少数据维度和提取主要特征的重要步骤。从矩阵角度来看，最大池化和平均池化操作可以看作是对输入矩阵的一种局部区域的统计操作。例如，对于一个二维输入矩阵，最大池化操作会在每个指定大小的局部区域内选择最大值作为输出，这相当于对矩阵的局部子矩阵进行操作。通过分析池化操作对矩阵特征的影响，可以更好地理解 CNN 的特征提取能力和数据降维效果。

（三）CNN 中的特征图与矩阵变换

在 CNN 中，经过卷积和池化操作后得到的特征图也是以矩阵形式存在。这些特征图之间的关系以及它们在网络中的传播可以通过矩阵变换来描述。例如，随着网络层数的增加，特征图的尺寸逐渐减小，而通道数逐渐增加，这一过程可以看作是一系列的矩阵变换。通过研究这些矩阵变换的性质，可以分析 CNN 的层次化特征表示能力和模型的复杂度。

五、矩阵论在循环神经网络（RNN）及其变体中的应用

（一）RNN 的矩阵表示与计算

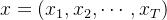
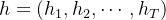
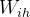
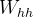
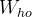
循环神经网络用于处理序列数据，其核心是一个循环单元，在每个时间步对输入数据进行处理。从矩阵角度来看，RNN 的计算可以用矩阵乘法和递归公式来表示。设输入序列为 $x=(x_1,x_2,\cdots,x_T)$ ，隐藏状态序列为 $h=(h_1,h_2,\cdots,h_T)$ ，权重矩阵为 $W_{ih}$ 、 $W_{hh}$ 和 $W_{ho}$ ，则隐藏状态的更新公式可以表示为 $h_t = \tanh(W_{ih}x_t + W_{hh}h_{t - 1})$ ，输出 $y_t = W_{ho}h_t$ 。这里的矩阵乘法和非线性函数（如 $\tanh$ ）的组合实现了对序列信息的处理和传递，通过矩阵运算可以高效地计算整个序列的输出。

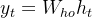
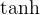
（二）长短期记忆网络（LSTM）和门控循环单元（GRU）中的矩阵操作

LSTM 和 GRU 是 RNN 的变体，用于解决 RNN 的长期依赖问题。在 LSTM 中，引入了输入门、遗忘门和输出门，这些门的计算都是通过矩阵乘法和非线性激活函数实现的。例如，遗忘门的计算为，其中和是相应的权重矩阵和偏置向量，是 sigmoid 函数。通过这些门的矩阵操作，LSTM 可以有选择地遗忘或更新信息，更好地处理长序列数据。GRU 也有类似的基于矩阵运算的结构，通过更新门和重置门来控制信息的流动。

（三）RNN 训练中的矩阵求导与梯度计算

在训练 RNN 及其变体时，需要计算损失函数关于模型参数的梯度。由于 RNN 的递归性质，梯度计算涉及到时间反向传播（BPTT）算法，这一过程中需要对矩阵求导。例如，在计算损失函数对权重矩阵的梯度时，需要根据链式法则对每个时间步的隐藏状态和输出进行求导，这一过程涉及到复杂的矩阵乘法和求导规则。通过正确应用矩阵求导法则和利用矩阵运算的性质，可以有效地计算梯度，实现模型的训练。

六、矩阵分解在深度学习模型压缩和加速中的应用

（一）奇异值分解（SVD）用于全连接层压缩

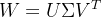
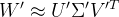
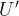
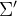
在深度学习模型中，全连接层通常占据大量的参数。奇异值分解可以用于对全连接层的权重矩阵进行压缩。对于一个全连接层的权重矩阵 W，通过 SVD 分解 $W = U\Sigma V^T$ ，可以选择保留较大的奇异值，将权重矩阵近似表示为 $W'\approx U'\Sigma'V'^T$ ，其中 $U'$ 、 $\Sigma'$ 和 $V'^T$ 是保留了部分信息的矩阵。这样可以大大减少全连接层的参数数量，同时在一定程度上保持模型的性能，从而实现模型的压缩和加速。

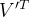
（二）低秩分解技术在卷积神经网络中的应用

对于卷积神经网络中的卷积核，也可以采用低秩分解技术来减少参数。例如，将卷积核矩阵分解为两个或多个低秩矩阵的乘积。这种分解方式可以降低卷积核的复杂度，减少模型的存储和计算量。同时，通过调整分解的秩，可以在模型压缩和性能之间进行权衡，提高深度学习模型在资源受限环境下的应用能力。

（三）张量分解在深度学习中的潜在应用

除了矩阵分解，张量分解技术在处理深度学习中的高维数据（如三维或更高维的张量表示的图像或视频数据）方面也具有潜在的应用价值。通过将高维张量分解为低维张量的组合，可以挖掘数据的内在结构，减少模型参数，实现更高效的深度学习算法设计。

七、矩阵论在处理深度学习大规模数据和高维特征方面的优势

（一）高效的矩阵乘法与并行计算

在深度学习中，面对大规模的数据和复杂的模型，高效的计算至关重要。矩阵乘法作为深度学习中最基本的运算之一，可以通过现代计算架构（如 GPU）实现高度并行化。GPU 具有大量的计算核心，可以同时处理多个矩阵元素的乘法运算，大大提高了计算速度。此外，一些先进的矩阵乘法算法（如 Strassen 算法及其改进版本）可以进一步优化计算复杂度，减少计算时间，使得深度学习模型能够在合理的时间内处理大规模数据。

（二）矩阵特征分析与降维技术

深度学习中经常会遇到高维特征问题，如高分辨率图像、大规模文本数据等。矩阵特征分析技术（如主成分分析 PCA，其基于矩阵的协方差矩阵特征值分解）可以用于降维。通过将高维数据投影到低维空间，同时保留数据的主要特征，可以减少数据的存储空间和计算复杂度。这不仅有利于模型的训练和推理，还可以缓解过拟合问题，提高模型的泛化能力。

（三）矩阵理论在分布式深度学习中的应用

随着深度学习模型规模的不断扩大，单机处理能力可能无法满足需求，分布式深度学习应运而生。在分布式环境中，数据和模型参数分布在多个计算节点上，矩阵论为数据划分、模型并行和通信优化提供了理论支持。例如，通过合理地将矩阵形式的数据划分为多个子矩阵，并在不同节点上进行计算，可以实现并行处理，提高训练效率。同时，矩阵论可以帮助设计高效的通信协议，减少节点之间的通信开销，保证分布式深度学习系统的高效运行。

八、结论与展望

矩阵论在深度学习的各个方面都有着不可或缺的应用。从模型训练算法的优化、不同类型神经网络（CNN、RNN 及其变体）的计算和分析，到模型压缩和加速技术，以及处理大规模数据和高维特征的方法，矩阵论为深度学习提供了强大的数学工具。随着深度学习技术的不断发展，如更复杂的网络架构的出现、对模型可解释性的要求提高以及在边缘计算等资源受限环境下的应用需求增加，矩阵论将继续在新的挑战中发挥关键作用。未来的研究方向可能包括进一步优化矩阵运算算法以适应新型硬件架构、开发更有效的基于矩阵分解的模型压缩方法、深入研究矩阵论在融合多模态数据的深度学习中的应用等，这些方向将推动深度学习技术向更高效、更智能的方向发展。

九、代码示例

以下是一个示例代码，展示了矩阵论在深度学习中的一些简单应用，这里以一个简单的全连接神经网络为例，包含了模型参数的矩阵表示、梯度下降优化算法中涉及的矩阵运算等方面：

#include <iostream>
#include <vector>
#include <cmath>
#include <ctime>
#include <cstdlib>

// 激活函数：Sigmoid函数
double sigmoid(double x) {
    return 1.0 / (1.0 + std::exp(-x));
}

// 神经网络类
class NeuralNetwork {
private:
    // 输入层、隐藏层、输出层的神经元数量
    int input_size;
    int hidden_size;
    int output_size;

    // 权重矩阵和偏置向量
    std::vector<std::vector<double>> weights_ih; // 输入层到隐藏层的权重矩阵
    std::vector<double> biases_h; // 隐藏层的偏置向量
    std::vector<std::vector<double>> weights_ho; // 隐藏层到输出层的权重矩阵
    std::vector<double> biases_o; // 输出层的偏置向量

public:
    NeuralNetwork(int input_s, int hidden_s, int output_s) :
        input_size(input_s), hidden_size(hidden_s), output_size(output_s) {
        // 随机初始化权重矩阵和偏置向量
        weights_ih.resize(input_size, std::vector<double>(hidden_size));
        biases_h.resize(hidden_size);
        weights_ho.resize(hidden_size, std::vector<double>(output_size));
        biases_o.resize(output_size);

        std::srand(static_cast<unsigned int>(std::time(nullptr)));
        for (int i = 0; i < input_size; ++i) {
            for (int j = 0; j < hidden_size; ++j) {
                weights_ih[i][j] = static_cast<double>(std::rand()) / RAND_MAX;
            }
        }
        for (int i = 0; i < hidden_size; ++i) {
            biases_h[i] = static_cast<double>(std::rand()) / RAND_MAX;
        }
        for (int i = 0; i < hidden_size; ++i) {
            for (int j = 0; j < output_size; ++j) {
                weights_ho[i][j] = static_cast<double>(std::rand()) / RAND_MAX;
            }
        }
        for (int i = 0; i < output_size; ++i) {
            biases_o[i] = static_cast<double>(std::rand()) / RAND_MAX;
        }
    }

    // 前向传播
    std::vector<double> forward_propagation(const std::vector<double>& inputs) {
        // 计算输入层到隐藏层的输出
        std::vector<double> hidden_layer_inputs(input_size);
        for (int i = 0; i < input_size; ++i) {
            hidden_layer_inputs[i] = inputs[i];
        }
        std::vector<double> hidden_layer_outputs(hidden_size);
        for (int i = 0; i < hidden_size; ++i) {
            double sum = 0.0;
            for (int j = 0; j < input_size; ++j) {
                sum += weights_ih[j][i] * hidden_layer_inputs[j];
            }
            sum += biases_h[i];
            hidden_layer_outputs[i] = sigmoid(sum);
        }

        // 计算隐藏层到输出层的输出
        std::vector<double> output_layer_inputs(hidden_size);
        for (int i = 0; i < hidden_size; ++i) {
            output_layer_inputs[i] = hidden_layer_outputs[i];
        }
        std::vector<double> predicted_outputs(output_size);
        for (int i = 0; i < output_size; ++i) {
            double sum = 0;
            for (int j = 0; j < hidden_size; ++j) {
                sum += weights_ho[j][i] * output_layer_inputs[j];
            }
            sum += biases_o[i];
            predicted_outputs[i] = sigmoid(sum);
        }

        return predicted_outputs;
    }

    // 计算损失函数（均方误差）
    double calculate_loss(const std::vector<double>& inputs, const std::vector<double>& targets) {
        std::vector<double> outputs = forward_propagation(inputs);
        double loss = 0.0;
        for (int i = 0; i < output_size; ++i) {
            double error = targets[i] - outputs[i];
            loss += error * error;
        }
        return loss / output_size;
    }

    // 反向传播
    void back_propagation(const std::vector<double>& inputs, const std::vector<double>& targets) {
        // 前向传播获取各层输出
        std::vector<double> hidden_layer_inputs(input_size);
        for (int i = 0; i < input_size; ++i) {
            hidden_layer_inputs[i] = inputs[i];
        }
        std::vector<double> hidden_layer_outputs(hidden_size);
        for (int i = 0; i < hidden_size; ++i) {
            double sum = 0.0;
            for (int j = 0; j < input_size; ++j) {
                sum += weights_ih[j][i] * hidden_layer_inputs[j];
            }
        }
        std::vector<double> output_layer_inputs(hidden_size);
        for (int i = 0; i < hidden_size; ++i) {
            output_layer_inputs[i] = hidden_layer_outputs[i];
        }
        std::vector<double> predicted_outputs(output_size);
        for (int i = 0; i < output_size; ++i) {
            double sum = 0;
            for (int j = 0; j < hidden_size; ++j) {
                sum += weights_ho[j][i] * output_layer_inputs[j];
            }
            sum += biases_o[i];
            predicted_outputs[i] = sigmoid(sum);
        }

        // 计算输出层的误差
        std::vector<double> output_layer_errors(output_size);
        for (int i = 0; i < output_size; ++i) {
            output_layer_errors[i] = (targets[i] - predicted_outputs[i]) * predicted_outputs[i] * (1 - predicted_outputs[i]);
        }

        // 计算隐藏层的误差
        std::vector<double> hidden_layer_errors(hidden_size);
        for (int i = 0; i < hidden_size; ++i) {
            double sum = 0;
            for (int j = 0; j < output_size; ++j) {
                sum += weights_ho[j][i] * output_layer_errors[j];
            }
            hidden_layer_errors[i] = sum * hidden_layer_outputs[i] * (1 - hidden_layer_outputs[i]);
        }

        // 更新隐藏层到输出层的权重和偏置
        for (int i = 0; i < hidden_size; ++i) {
            for (int j = 0; j < output_size; ++i) {
                weights_ho[i][j] += learning_rate * output_layer_errors[j] * output_layer_inputs[i];
            }
            biases_o[i] += learning_rate * output_layer_errors[i];
        }

        // 更新输入层到隐藏层的权重和偏置
        for (int i = 0; i < input_size; ++i) {
            for (int j = 0; j < hidden_size; ++i) {
                weights_ih[i][j] += learning_rate * hidden_layer_errors[j] * hidden_layer_inputs[i];
            }
            biases_h[i] += learning_rate * hidden_layer_errors[i];
        }
    }

    // 设置学习率
    double learning_rate = 0.01;
};

int main() {
    // 创建一个简单的神经网络实例
    NeuralNetwork nn(2, 3, 1);

    // 训练数据
    std::vector<std::vector<double>> training_data = {
        {0.0, 0.0},
        {0.0, 1.0},
        {1.0, 0.0},
        {1.0, 1.0}
    };
    std::vector<std::vector<double>> training_targets = {
        {0.0},
        {1.0},
        {1.0},
        {0.0}
    };

    // 训练循环
    for (int epoch = 0; epoch < 1000; ++epoch) {
        double total_loss = 0.0;
        for (int i = 0; i < training_data.size(); ++i) {
            total_loss += nn.calculate_loss(training_data[i], training_targets[i]);
            nn.back_propagation(training_data[i], training_targets[i]);
        }
        if (epoch % 100 == 0) {
            std::cout << "Epoch " << epoch << " - Loss: " << total_loss / training_data.size() << std::endl;
        }
    }

    // 测试数据
    std::vector<std::vector<double>> test_data = {
        {0.0, 0.0},
        {0.0, 1.0},
        {1.0, 0.0},
        {1.0, 1.0}
    };

    // 测试神经网络
    for (int i = 0; i < test_data.size(); ++i) {
        std::vector<double> output = nn.forward_propagation(test_data[i]);
        std::cout << "Input: " << test_data[i][0] << ", " << test_data[i][1] << " - Output: " << output[0] << std::endl;
    }

    return 0;
}

在这个示例代码中：

1. 模型参数的矩阵表示

weights_ih 是输入层到隐藏层的权重矩阵，其维度是 input_size（输入层神经元数量）乘以 hidden_size（隐藏层神经元数量）。
weights_ho 是隐藏层到输出层的权重矩阵，维度为 hidden_size 乘以 output_size（输出层神经元数量）。
biases_h 和 biases_o 分别是隐藏层和输出层的偏置向量，它们在某种程度上也可以看作是与权重矩阵协同工作的特殊 “矩阵”（在代码实现中以向量形式存在，但在概念上与矩阵运算相关联）。

2. 前向传播中的矩阵运算

在 forward_propagation 函数中，计算隐藏层和输出层的输出时，涉及到大量的矩阵乘法和加法运算。例如，计算隐藏层输出时，通过遍历输入层神经元和隐藏层神经元，将输入层的每个元素与对应的权重矩阵元素相乘，并累加偏置向量的值，最后通过激活函数（这里是 Sigmoid 函数）得到隐藏层输出。这一过程本质上是矩阵乘法（权重矩阵与输入向量相乘）加上向量加法（加上偏置向量）的操作。

3. 反向传播中的矩阵运算及梯度计算

在 back_propagation 函数中，首先通过前向传播获取各层输出，然后计算输出层和隐藏层的误差。计算误差的过程涉及到根据损失函数（这里是均方误差）对输出进行求导，这也与矩阵运算相关（例如，在计算输出层误差时，根据 Sigmoid 函数的导数公式以及损失函数对输出的求导规则进行计算）。
接着，根据误差来更新权重矩阵和偏置向量。更新过程同样涉及到大量的矩阵乘法和加法运算，例如，更新隐藏层到输出层的权重时，将学习率乘以输出层误差与隐藏层输入的乘积，并累加到当前权重矩阵元素上。

4. 训练过程中的整体矩阵相关操作

在 main 函数中，通过循环进行训练，每次迭代都会调用 calculate_loss 和 back_propagation 函数，这其中不断地进行着上述的矩阵运算、误差计算以及权重和偏置的更新操作，以逐步优化神经网络的参数，使其能够更好地拟合训练数据。

虽然这个示例是一个相对简单的全连接神经网络实现，但它展示了矩阵论在深度学习中一些基本方面的应用，如模型参数的矩阵表示、前向传播和反向传播中的矩阵运算等。在实际的深度学习框架（如 TensorFlow、PyTorch 等）中，这些矩阵相关的操作会被更加高效地实现和优化，并且会涉及到更多复杂的应用场景和技术，比如卷积神经网络中的卷积核矩阵运算、循环神经网络中的递归矩阵计算等。