简单题
一分类:数组
1.两数之和(哈希表)
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
var targetNum=[];
for(var i=0;i<nums.length-1;i++){
for(var j=i+1;j<nums.length;j++){
if(nums[i]+nums[j]===target){
targetNum.push(i);
targetNum.push(j);
break;
}
}
}
return targetNum;
};
2.最大子数组和(贪心算法、动态规划)
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
动态规划:若前一个元素>0,则将其加到当前元素上(保证只加正数)
/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
//动态规划,判断之前和是否小于0,小于0不累加
var curSum=nums[0];
var max=nums[0];
for(var i=1;i<nums.length;i++){
if(curSum<0){
curSum=nums[i]
}else{
curSum=curSum+nums[i]
}
if(curSum>max){
max=curSum
}
}
return max;
};
贪心算法:若当前指针所指元素之前和<0,则丢弃当前元素之前是数列(更新指针)
/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
//贪心算法:若当前指针i所指元素之前和<0,则丢弃当前元素之前是数列(更新指针)
var value=nums[0]; //当前值
var curSum=null;//之前和
var nowSum=nums[0];//当前和
var max=nums[0];//最大值
//遍历数组,从第二个开始遍历
for(var i=1;i<nums.length;i++){
//更新当前值,之前和
value=nums[i];
curSum=nowSum;
//先判断之前和是否小于0
if(curSum<0){//小于0,丢弃之前和,令之前和=当前值
nowSum=value;
}else if (curSum>=0) {//大于0,累加之前和和当前值
nowSum=curSum+value;
}
if(nowSum>max){//若max小于当前和,更新max
max=nowSum
}
}
return max;
};
3.买卖股票的最佳时机(数组、动态规划、贪心算法)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
贪心算法
1.先定义最低价格和利润
2.遍历数组,更新最低价格和利润
3.最后遍历完成,返回利润
善用Math.min与Math.max这两个方法
// 先定义第一天为最低价格
let min = prices[0];
// 利润
let profit = 0;
// 遍历数据
for (let i = 1; i < prices.length; i++) {
// 如果发现比最低价格还低的,更新最低价格
min = Math.min(min, prices[i]);
// 如果发现当前利润比之前高的,更新利润
profit = Math.max(profit, prices[i] - min);
}
return profit;
4.只出现一次的数字(位运算)
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
简单的遍历数组,再建立一个数组保存遍历的值,如果该值已存在,便移除,最后只剩下一个
判断judgeNum数组中是否存在nums[i]元素:judgeNum.indexOf(nums[i])
存在的话会返回该元素下标,利用该下标移除该重复元素judgeNum.splice(index, 1);
不存在返回-1,加进数组中judgeNum.push(nums[i])
var judgeNum=[]
for(var i=0;i<nums.length;i++){
let index=judgeNum.indexOf(nums[i])
if(index===-1){//该元素不在judgeNum数组里
judgeNum.push(nums[i])
}else{//存在该元素,并且会返回该元素存在的下标
judgeNum.splice(index, 1);
}
}
return judgeNum[0];
5.异或
异或的性质:交换律、结合律、自反性。“异或”用人话来说就是“找不同”,比如两幅图找不同,不同的点才为true,相同的部分为false。
let ans = 0;
for(let i = 0; i < nums.length; i++){
ans ^= nums[i];
}
return ans;
6.汉民距离(位运算)
var hammingDistance = function (x, y) {
//将x和y转换成二进制的
x = x.toString(2);
y = y.toString(2);
//补零
let maxLength = Math.max(x.length, y.length);
//es6的方法
x = x.padStart(maxLength, 0);
y = y.padStart(maxLength, 0);
let sum = 0;
for (let i = 0; i < maxLength; i++) {
if (x[i] != y[i]) {
sum++;
}
}
return sum;
};
7.移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
var moveZeroes = function(nums) {
let i=0
//创建两个指针,把非0元素交换到前面来
for(let i=0;i<nums.length-1;i++){
for(let j=i+1;j<nums.length;j++){
if(nums[i]===0&&nums[j]!=0){
let change=nums[i]
nums[i]=nums[j]
nums[j]=change
}
}
}
return nums;
};
8.比特位计算
首先我们要发现规律
var countBits = function(n) {
result =[0];
for(let i = 1; i <= n; i++)
{
if(i % 2 == 1)
{
result[i] = result[i-1] + 1;
}
else
{
result[i] = result[i/2];
}
}
return result;
};
9.找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
直接遍历1-n,查看哪个元素不在数组里面(虽然简单,但执行用时较长)
var findDisappearedNumbers = function(nums) {
let arr = [];
for (let i = 1; i < nums.length+1;i++) {
if(nums.indexOf(i)==-1){
arr.push(i)
}
}
return arr;
};
10.多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
暴力循环:用对象键值对记录数组中某元素出现的次数,再遍历对象键值对将出现次数大于n/2的元素找出来
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function(nums) {
var frequency = {};
for (var i = 0; i < nums.length; i++) {
var item = nums[i];
if (frequency[item]) {
frequency[item]++;
} else {
frequency[item] = 1;
}
}
for(var j in frequency){
if(frequency[j]>nums.length/2){
return j
}
}
};
更简便方法:如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为⌊ n/2 ⌋ 的元素(下标从 0 开始)一定是众数。
var majorityElement = function(nums) {
nums= nums.sort()
var index=parseInt(nums.length/2)
return nums[index]
};
二分类:动态规划、记忆化搜索
动态规划
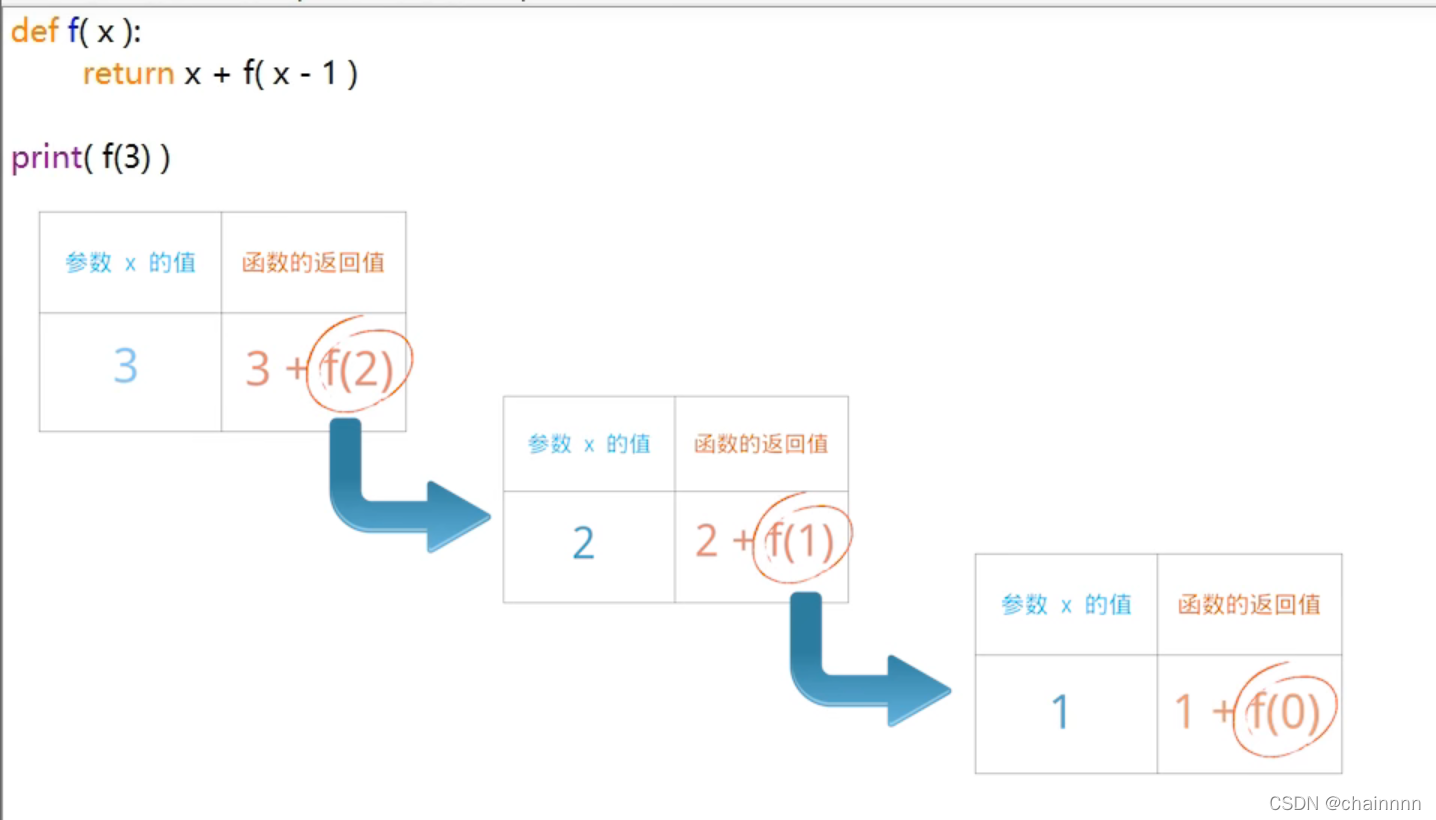
1.爬楼梯(动态规划)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
难点:我们可以通过在 n-1 阶的那块一次性爬 1 步来达到 n 楼层,以及通过在 n - 2 阶 一次性爬 2 步来达到 n 楼层。所以就是这两种情况的总和。我们可以列出如下式子:f(n) = f(n - 1) + f(n - 2)
/**
* @param {number} n
* @return {number}
*/
var climbStairs = function(n) {
if(n == 1){return 1;}
if(n == 2){return 2;}
//a 表示第n-2个台阶的走法,b表示第n-1个台阶的走法,传统迭代
let a=1 , b=2, temp;
//从第三个台阶开始
for(var i=3;i<=n;i++){
//累加
temp=a+b;
//更新a、b
a=b;//下次迭代的第n-2个台阶的走法等于上次迭代n-1个台阶的走法
b=temp;//下次迭代的第n-1个台阶的走法等于上次迭代的第n个台阶走法
}
return temp;
};
三分类:栈、字符串
1.有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
**难点:
1.遍历字符串,使用for of;
2.栈 Stack.peek()与Stack.pop()
pop():返回栈顶的值 ;会把栈顶的值删除。
poll:Queue(队列)的一个方法,获取并移除此队列的头,如果此队列为空,则返回null。
peek():返回栈顶的值 ;不改变栈的值,查看栈顶的对象而不移除它。
操作:
遍历字符串,
1.首先判断是否为左括号>是进栈stack.push(char)
2.不是为右括号>看栈顶元素stack.pop()是否为对应的左括号
3.不是直接返回false
4.重复操作
5.遍历完成判断栈内元素是否为空
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function(s) {
var stack=[];
for(let char of s){
if(char==="("||char==="["||char==="{"){
stack.push(char)
}else{
if(char===")"&&stack.pop()!=="("){return false}
if(char==="]"&&stack.pop()!=="["){return false}
if(char==="}"&&stack.pop()!=="{"){return false}
}
}
return !stack.length
};
2.最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
思路:
有两个栈,一个数据栈,一个最小栈
入栈时,如果最小栈为空,或者新元素小于或等于最小栈栈顶,则将新元素压入最小栈
出栈时,如果出栈元素和最小栈栈顶元素值相等,最小栈出栈
/**
* initialize your data structure here.
*/
var MinStack = function () {
this.data_stack = [];
this.min_stack = [];
};
/**
* @param {number} val
* @return {void}
*/
MinStack.prototype.push = function (val) {
this.data_stack.push(val);
// 如果最小栈为空,或者新元素小于或等于最小栈栈顶,则将新元素压入最小栈(备注:这里一定是小于等于 而非小于)
if (
!this.min_stack.length ||
val <= this.min_stack[this.min_stack.length - 1]
) {
this.min_stack.push(val);
}
};
/**
* @return {void}
*/
MinStack.prototype.pop = function () {
// 如果出栈元素和最小栈栈顶元素值相等,最小栈出栈
if (
this.data_stack[this.data_stack.length - 1] ==
this.min_stack[this.min_stack.length - 1]
) {
this.min_stack.pop();
}
return this.data_stack.pop();
};
/**
* @return {number}
*/
MinStack.prototype.top = function () {
return this.data_stack[this.data_stack.length - 1];
};
/**
* @return {number}
*/
MinStack.prototype.getMin = function () {
return this.min_stack[this.min_stack.length - 1];
};
/**
* Your MinStack object will be instantiated and called as such:
* var obj = new MinStack()
* obj.push(val)
* obj.pop()
* var param_3 = obj.top()
* var param_4 = obj.getMin()
*/
四分类:递归、链表
递归解释
由于函数会永无止境的调用,所以需要边界条件
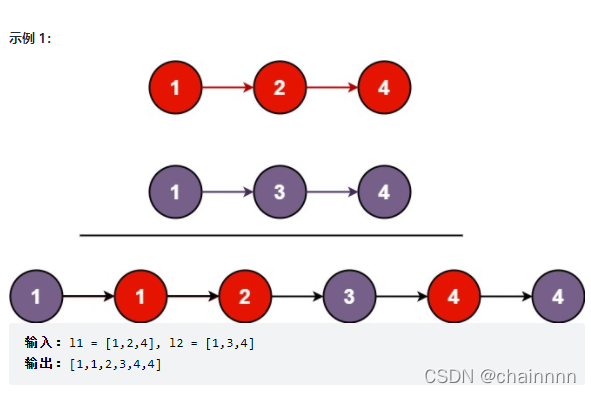
1. 合并两个有序链表
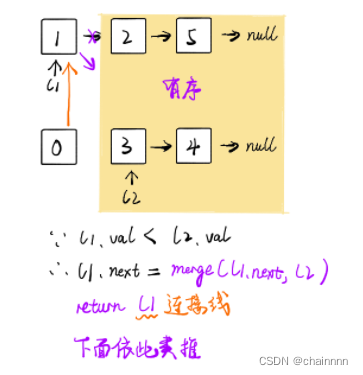
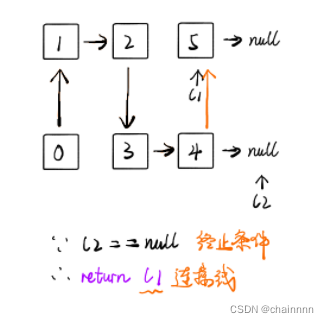
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
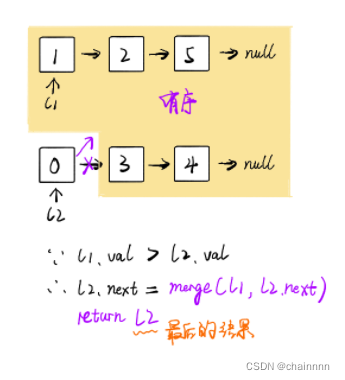
如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空,递归结束。
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} list1
* @param {ListNode} list2
* @return {ListNode}
*/
var mergeTwoLists = function(list1, list2) {
if(list1==null){
return list2
}else if(list2==null){
return list1
}else if(list1.val<list2.val){
list1.next=mergeTwoLists(list1.next,list2)
return list1;
}
else{
list2.next=mergeTwoLists(list1,list2.next)
return list2;
}
};
2.环形链表
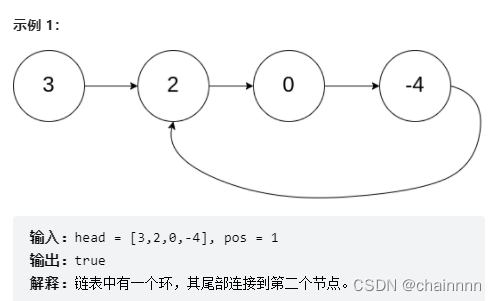
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
方法一:快慢指针
这属于数学上的追及问题。两个运动员在环形跑道跑步,匀速,速度快的一定会追上速度慢的。
/**
* @param {ListNode} head
* @return {boolean}
*/
var hasCycle = function(head) {
if (head == null || head.next == null) {
return false;
}
let slow = head;
let fast = head.next;
while (slow != fast) {
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true
};
方法二: 最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
var hasCycle = function (head) {
if(head==null||head.next==null){
return false
}
let stack=[]
while(head){
if(stack.includes(head)){
return true
}
stack.push(head)
head=head.next
}
return false
};
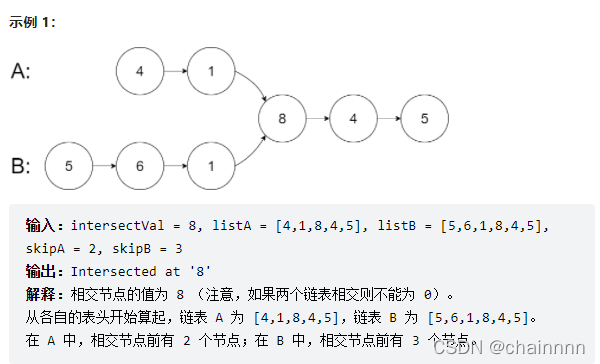
3.相交链表(哈希表、链表、双指针)
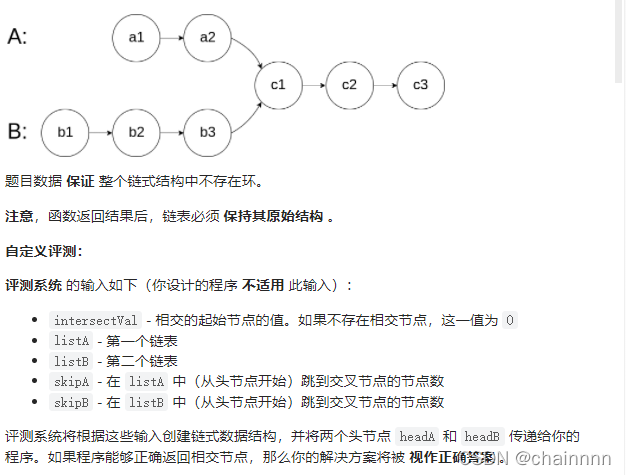
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
双指针:
使用双指针的方法,可以将空间复杂度降至 O(1)O(1)。
var getIntersectionNode = function(headA, headB) {
if (headA === null || headB === null) {
return null;
}
let pA = headA, pB = headB;
while (pA !== pB) {//重点,当pA遍历到headA的结尾,接着遍历headB
pA = pA === null ? headB : pA.next;
pB = pB === null ? headA : pB.next;
}
return pA;
};
4.反转链表(迭代 )
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
在遍历链表时,将当前节点的next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
var reverseList = function(head) {
let prev = null;
let curr = head;
while (curr) {
let next=curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
};
树、栈、深度优先搜索
1.二叉树的中序遍历(迭代)
二叉树的中序遍历:按照访问左子树——根节点——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候我们按照同样的方式遍历,直到遍历完整棵树
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
//结果数组
var res=[];
//当前保存节点的栈
var stk=[];
//当前仍有节点或者栈内还有节点没有出栈保存到res中
while(root||stk.length){
//循环节点
while(root){
//有节点的话进栈,进栈完更新root节点信息
stk.push(root)
//更新root,为当前节点的左节点
root=root.left;
}
//当左节点循环到底会跳出循环,当前root就是最终的左节点,需要出栈
root= stk.pop()
//将弹出的节点的值保存到res数组中
res.push(root.val)
//将root更新到该root的右节点
root=root.right;
}
return res;
};
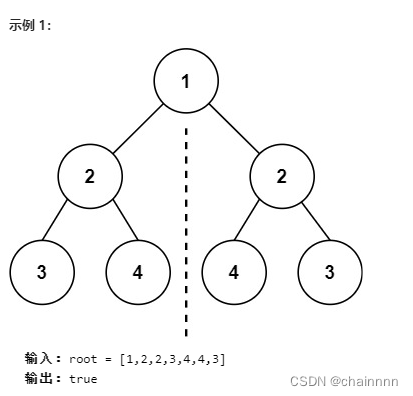
2.对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
比较节点个数是否相等,节点的值是否相等
递归判断
var isSymmetric = function(root) {
//首先判断该树是否为空
if(root===null){
return true;
}
//使用递归遍历左右子树 递归三部曲
// 1. 确定递归的参数 root.left root.right和返回值true false
const compareNode=function(left,right){
//2. 确定终止条件,空的情况,只有一个节点
if(left===null&&right!=null||left!=null&&right===null){
return false;
}else if(left===null&&right===null){//该子树下都是空节点
return true
}else if(left.val!==right.val){//该子树下值不相等
return false;
}
//3. 确定单层递归逻辑
let outSide=compareNode(left.left,right.right);
let inSide=compareNode(left.right,right.left);
return outSide&&inSide;
}
return compareNode(root.left,root.right)
};
队列判断
var isSymmetric = function(root) {
//队列实现迭代判断
//首先判断root是否为空
if(root===null){
return true;
}
let queue=[];
queue.push(root.left);
queue.push(root.right);
//当队列里有节点时进行循环
while(queue.length){
//shift()方法是将一个数组的第一个元素移出
//取出队列里的左节点
let leftNode=queue.shift()
let rightNode=queue.shift()
if(leftNode===null&&rightNode===null){
continue;
}else if(leftNode===null&&rightNode!=null||leftNode!=null&&rightNode===null){
return false;
}else if(leftNode.val!==rightNode.val){//该子树下值不相等
return false;
}
queue.push(leftNode.left)//左节点左孩子入队
queue.push(rightNode.right)//右节点的有孩子入队
queue.push(leftNode.right)//左节点的右孩子入队
queue.push(rightNode.left)//右节点的左孩子入队
}
return true;
};
栈实现判断
var isSymmetric = function(root) {
//栈实现迭代判断
//首先判断root是否为空
if(root===null){
return true;
}
let stk=[];
stk.push(root.left);
stk.push(root.right);
//当队列里有节点时进行循环
while(stk.length){
//shift()方法是将一个数组的第一个元素移出
//取出队列里的左节点
let leftNode=stk.pop()
let rightNode=stk.pop()
if(leftNode===null&&rightNode===null){
continue;
}else if(leftNode===null&&rightNode!=null||leftNode!=null&&rightNode===null){
return false;
}else if(leftNode.val!==rightNode.val){//该子树下值不相等
return false;
}
stk.push(leftNode.left)//左节点左孩子入队
stk.push(rightNode.right)//右节点的有孩子入队
stk.push(leftNode.right)//左节点的右孩子入队
stk.push(rightNode.left)//右节点的左孩子入队
}
return true;
};
3. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
只需要判断其有没有节点,并且左右中最大值
int left = maxDepth(root.left);递归一次,left=1,n次,left =n
var maxDepth = function(root) {
if(!root) {
return 0;
} else {
const left = maxDepth(root.left);
const right = maxDepth(root.right);
return Math.max(left, right) + 1;
}
};
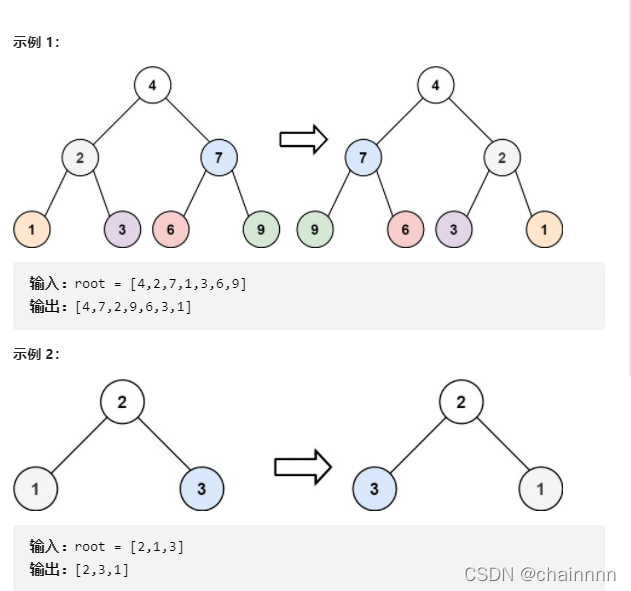
4.翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var invertTree = function(root) {
//递归函数的终止条件,节点为空时返回
if (root === null) {
return null;
}
//递归交换当前节点的左右子树
const left = invertTree(root.left);
const right = invertTree(root.right);
//将当前节点的左右子树交换
root.left = right;
root.right = left;
return root;
};
var invertTree = function(root) {
if (root === null) {
return null;
}
//先交换左右子树
const change=root.left;
root.left=root.right;
root.right=change
//递归交换当前节点的左右子树
invertTree(root.left)
invertTree(root.right)
return root
};
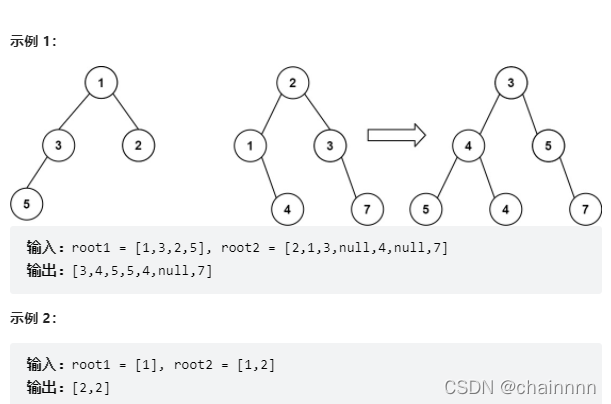
5.合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
var mergeTrees = function(root1, root2) {
if(root1===null){
return root2
}else if(root2===null){
return root1
}
root1.val=root1.val+root2.val;
root1.left= mergeTrees(root1.left,root2.left)
root1.right= mergeTrees(root1.right,root2.right)
return root1;
};
6. 二叉树的直径(深度优先搜索)
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
深度优先搜索:大多使用递归函数
递归函数三要素:
1.子问题与原问题做相同目标的事情
2.需要有一个让递归结束的出口
3.递归表达式
都经过根节点的情况:计算每个节点的深度多少
var diameterOfBinaryTree = function(root) {
const deep=function(root){
if(root===null){
return 0
}
let L,R;
L=deep(root.left)
R=deep(root.right)
return Math.max(L,R)+1;
}
return deep(root)
};
考虑题目:加上不经过根节点的情况
一开始设定一个局部变量Max来储存最大深度
var diameterOfBinaryTree = function(root) {
let Max=0;
const deep=function(root){
if(root===null){
return 0
}
let L,R;
L=deep(root.left)
R=deep(root.right)
if(L+R>Max){
Max=L+R
}
return Math.max(L,R)+1;
}
deep(root)
return Max
};
回文链表
用比较简单的方式是遍历链表,把里面的值一一保存到数组中,再循环数组,看看这个数组里面的值是不是相同的
var isPalindrome = function(head) {
let stack=[]
while(head){
stack.push(head.val)
head=head.next
}
for (let i = 0, j = stack.length - 1; i < j; ++i, --j) {
if (stack[i] !== stack[j]) {
return false;
}
}
return true
};