参考书籍：计算机视觉与深度学习实战:以MATLAB、Python为工具，
主编：刘衍琦, 詹福宇， 王德建
北京：电子工业出版社，2019

1 直方图均衡

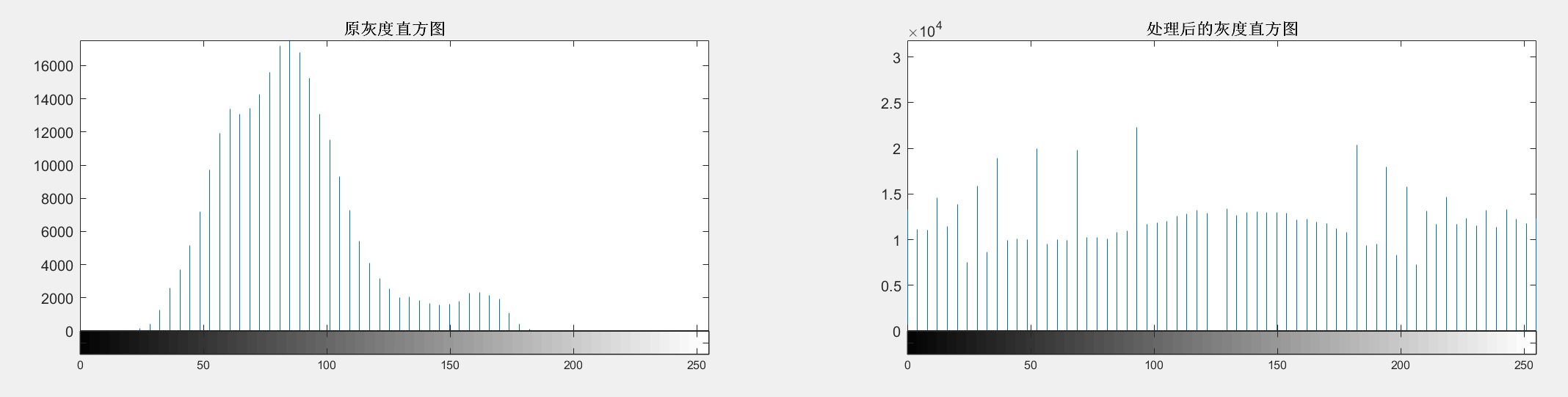
直方图是图像的一种统计表达形式。对于一幅灰度图像来说，其灰度统计直方图可以反映该图像中不同灰度级出现的统计情况。一般而言，图像的视觉效果和其直方图有对应关系，通过调整或变换其直方图的形状会对图像的显示效果有很大影响。

直方图均衡化主要用于增强灰度值动态范围偏小的图像的对比度，它的基本思想是把原始图像的灰度统计直方图变换为均匀分布形式，这样就增加了像素灰度值的动态范围，从而达到增强图像整体对比度的效果。

数字图像是离散化的数值矩阵，其直方图可以被视为一个离散函数，表示数字图像中每个灰度级与其出现概率间的统计关系。假设一幅数字图像 f(x,y)的像素总数为 N，r_k表示第 k 个灰度级对应的灰度，n_k表示灰度为r_k 的像素个数即频数，若用横坐标表示灰度级，用纵坐标表示频数，则直方图可被定义为P(r_k)=n_k/N，其中，P(r_k)表示第k灰度出现的相对频数即概率。直方图在一定程度上能够反映数字图像的概貌性描述，包括图像的灰度范围、灰度分布、整幅图像的亮度均值和阴暗对比度等,并可以此为基础进行分析来得出对图像进一步处理的重要依据直方图均衡化也叫作直方图均匀化，就是把给定图像的直方图变换成均匀分布的直方图，是一种较为常用的灰度增强算法。

根据信息论的相关理论，我们可以知道图像在经直方图均衡化后，将会包含更多的信息量进而能突出某些图像特征。假设图像具有 n级灰度，其第级灰度出现的概率为 P_i， 则该级度所含的信息量为:
$I(i)=p_i\log \frac{1}{p_i}=-p_i\log p_i$

整幅图像的信息最为：
$H={\sum }_{i=0}^{n-1}I(i)=-{\sum }_{i=0}^{n-1}{p}_i\log p_i$
信息论已经证明，具有均匀分布直方图的图像，其信息量H 最大。即当$P_0=P_1=...=P_{n-1}$时，H有最大值。

2 程序实现

% 灰度图直方图均衡
% 加载路径和所有文件
clc;clear;close all;
cd(fileparts(mfilename('fullpath')));
addpath(genpath(cd));

if ~isfolder('HistGraph')
    mkdir('HistGraph');
end

Path = '.\';                   % 设置数据存放的文件夹路径
File = dir(fullfile(Path,'*.jpg'));  % 显示文件夹下所有符合后缀名为.txt文件的完整信息
FileNames = {File.name}';            % 提取符合后缀名为.txt的所有文件的文件名，转换为n行1列

for i = 1:size(FileNames,1)
    I = imread(FileNames{i});
    R = I(:,:,1);
    M = histeq(R);

    In = M;
    
    figure;
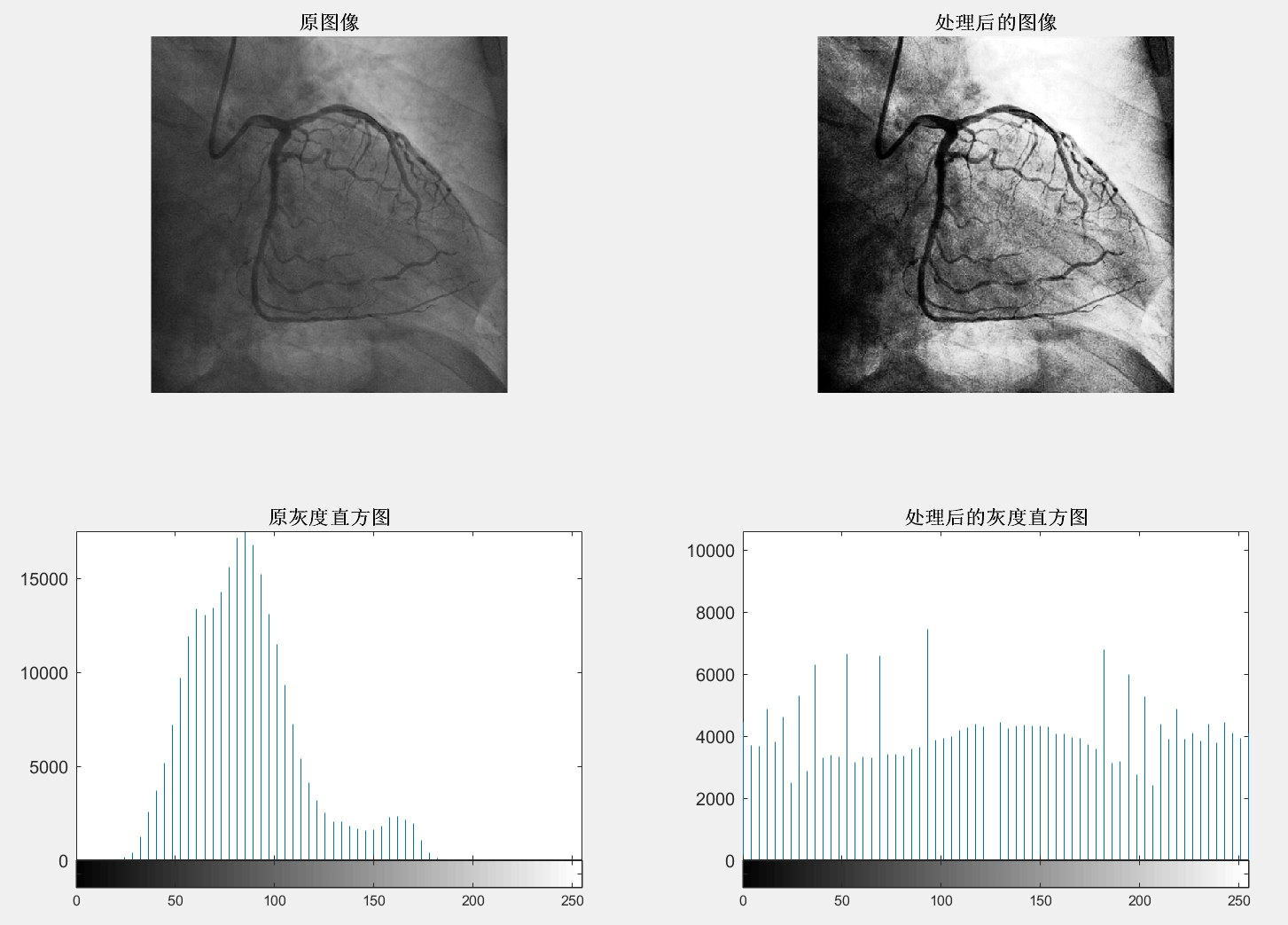
    subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');
    subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');
    imwrite(In,['HistGraph\',FileNames{i}],'jpg')
    
    Q = I; 
    W = In;
    subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
    subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');
end

% 彩色图直方图均衡
clear; close all;
I = imread('images\sweden_input.jpg');
R = I(:,:,1);
G = I(:,:,2);
B = I(:,:,3);
M = histeq(R);
N = histeq(G);
L = histeq(B);
In = cat(3, M, N, L);

figure;
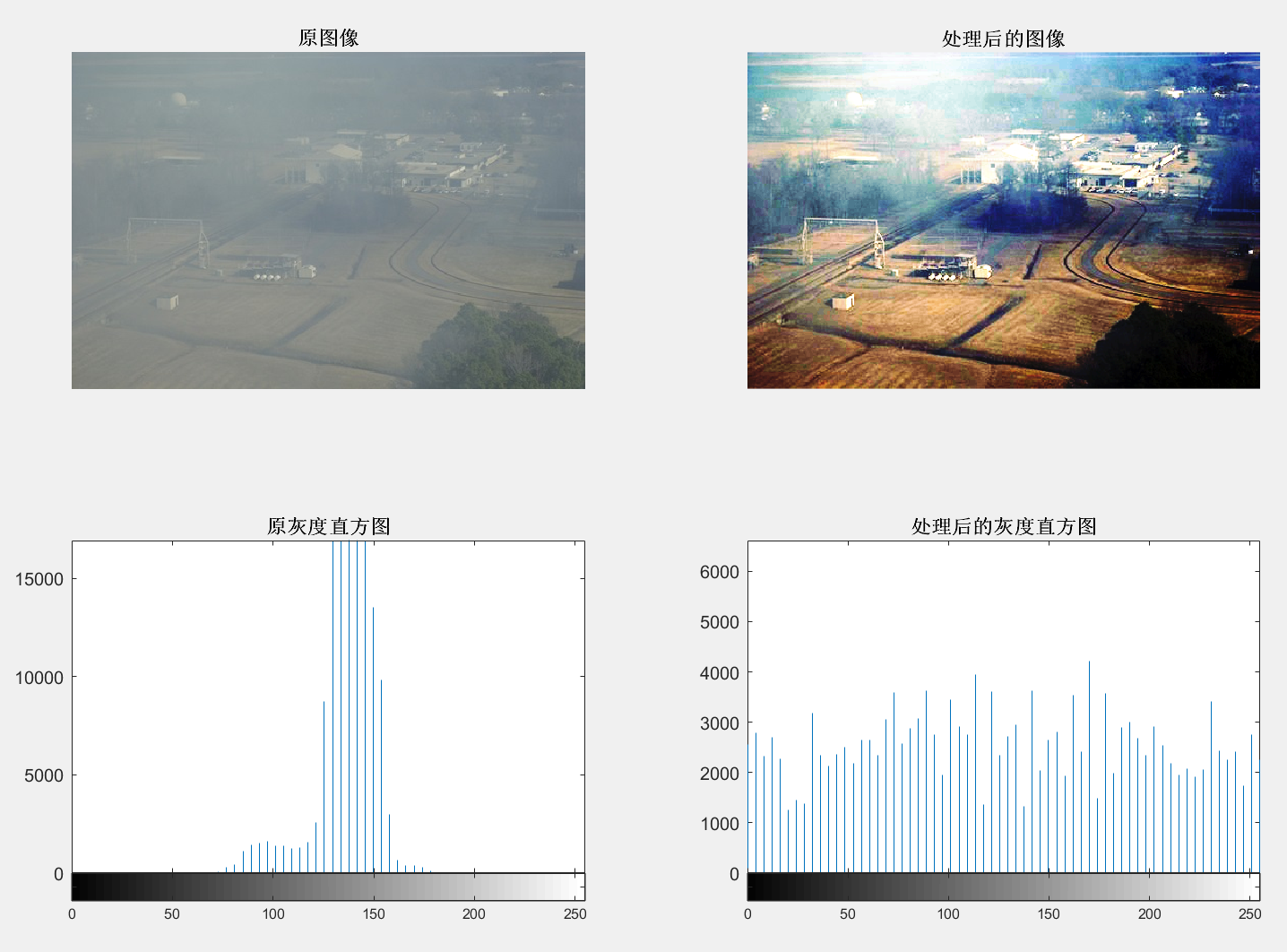
subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');
subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');

Q = rgb2gray(I);
W = rgb2gray(In);
subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');

全局直方图去雾效果明显，但在图像整体上容易出现色彩失真现象。

3 局部直方图处理

clear; close all;
I = imread('images\sweden_input.jpg');
g1 = GetLocalHisteq(I(:, :, 1));
g2 = GetLocalHisteq(I(:, :, 2));
g3 = GetLocalHisteq(I(:, :, 3));

In = cat(3, g1, g2, g3);

figure;
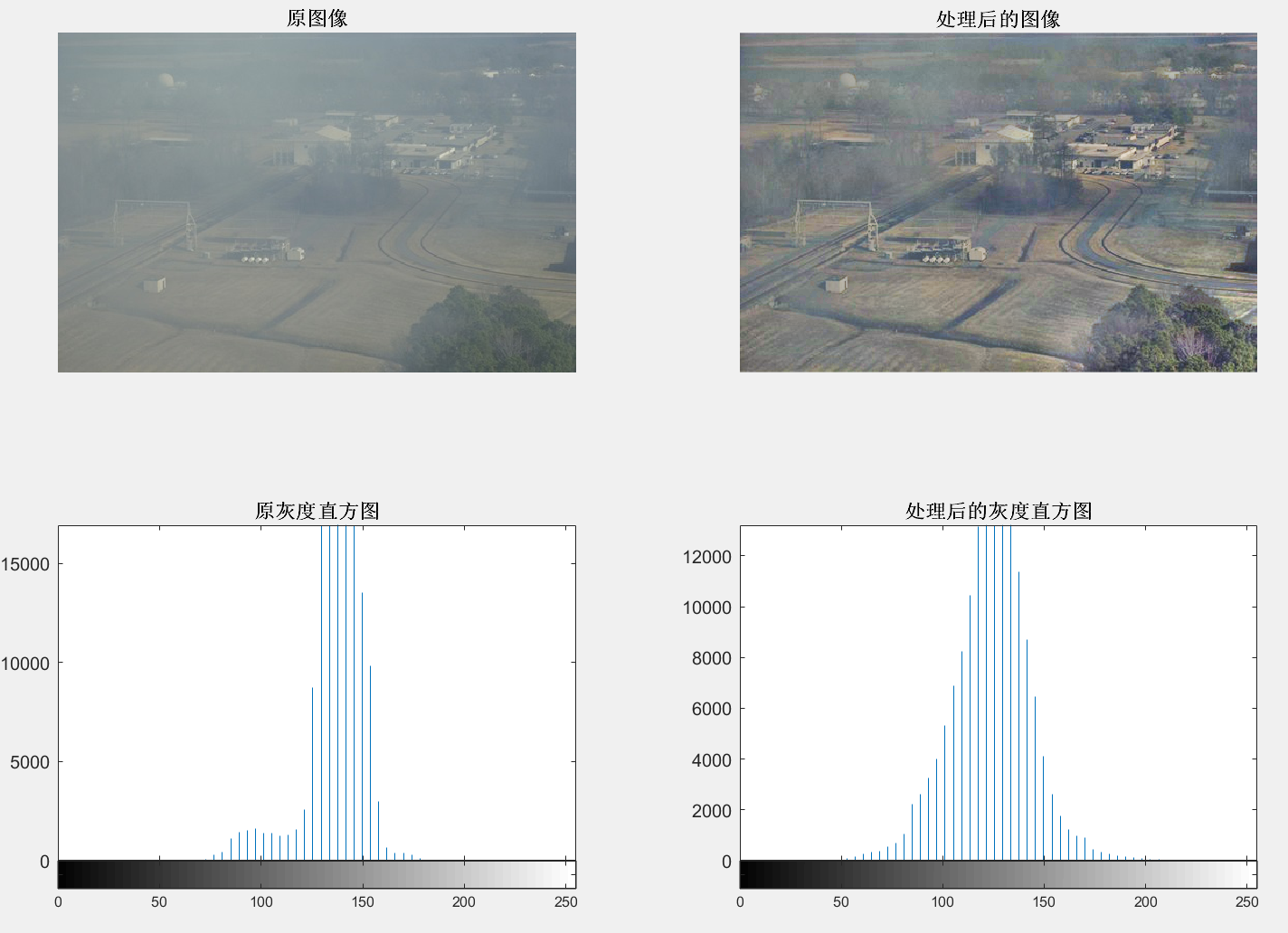
subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');
subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');
Q = rgb2gray(I);
W = rgb2gray(In);
subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');

function g = GetLocalHisteq(I)
% 对灰度图像，进行局部直方图均衡化
% 输入参数：
%  I——图像矩阵
% 输出参数：
%  g——结果图像
% 调用库函数adapthisteq，执行局部均衡化增强
g = adapthisteq(I,'clipLimit',0.02,'Distribution','rayleigh');
end

局部直方图的处理有效保持原图像的局部特征，未出现明显的色彩失真，但该图像整体的亮度偏暗，依然在某些区域模糊。