4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

分析

首先我们找到中位数，可能需要分析数组的个数是奇数还是偶数，但其实我们分别找第 (m+n+1) / 2 个，和 (m+n+2) / 2 个，然后求其平均值即可，这对奇偶数均适用。

因为当 m+n 为奇数的话，那么其实 (m+n+1) / 2 和 (m+n+2) / 2 的值相等， 相当于两个相同的数字相加再除以2，还是其本身。

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length,n = nums2.length;
        int left = (m+n+1)/2,right = (m+n+2)/2;
        return (findKth(nums1,0,nums2,0,left)+findKth(nums1,0,nums2,0,right))/2;
    }

    private double findKth(int[] nums1, int i, int[] nums2, int j, int k) {
        if (i == nums1.length) return nums2[j+k-1];
        if (j == nums2.length) return nums1[i+k-1];
        if (k == 1){
            return Math.min(nums1[i],nums2[j]);
        }
        int minVal1 = (i+k/2-1)<nums1.length? nums1[i+k/2-1]:Integer.MAX_VALUE;
        int minVal2 = (j+k/2-1)<nums2.length? nums2[j+k/2-1]:Integer.MAX_VALUE;
        if (minVal2 >minVal1){
            return findKth(nums1,i+k/2,nums2,j,k/2);
        }else {
            return findKth(nums1,i,nums2,j+k/2,k/2);
        }
    }

LC101. 对称二叉树

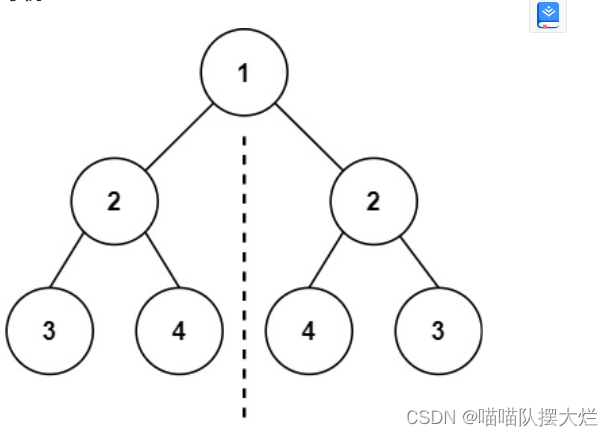
给你一个二叉树的根节点 root ， 检查它是否轴对称。

输入：root = [1,2,2,3,4,4,3]
输出：true

比较两棵子树是否对称。

如果用迭代的方式，可以使用 BFS 层序遍历，把每一层的节点求出来，然后用左右双指针判断每一层是否是对称的。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        // 检查两棵子树是否对称
        return check(root.left, root.right);
    }

    boolean check(TreeNode left, TreeNode right) {
        if (left == null || right == null) return left == right;
        // 两个根节点需要相同
        if (left.val != right.val) return false;
        // 左右子节点需要对称相同
        return check(left.right, right.left) && check(left.left, right.right);
    }
}