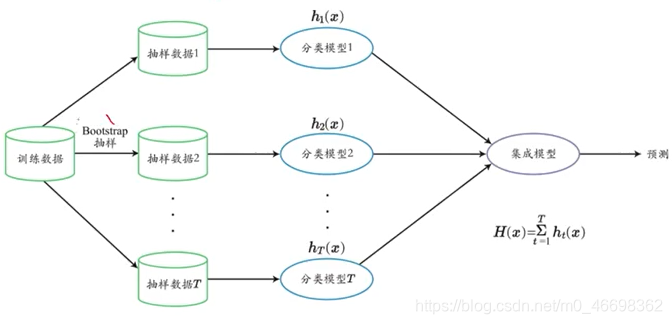
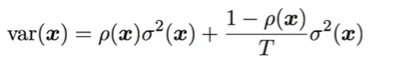Bagging是Bootstrap aggregating的缩写，该方法的核心包括自助抽样（boostrap）和平均（aggregating）

Bagging自助抽样过程

通过有放回抽样的方式，获取与原数据集D大小一样的样本集D_t。
给定n个样本的数据集D，对于迭代（t=1，2，…，T），用来创建分类器M_t,基于基分类器的投票返回类预测。一个样本有1-1/n的概率不会被选到，则一个样本不会被抽到的概率是
$$\underset{n\to \infty }{\lim }{\left(1-\frac{1}{n}\right)}^n=0.368$$
意味着训练集包含63.2%的不同的样本

Bagging提升过程

每个D_t学习得到一个分类器M_t。对于分类问题，每个分类器返回类预测，采用多数投票的方法；对于回归问题，采用平均值的方法。

Bagging算法

Bagging的优势

1.特别适合用来提高那些方差大但偏差小的基模型(决策树，神经网络等)的预测性能。
2.单个模型不稳定:对训练数据轻微的改变就能够造成分类器性能很明显的变化。
3.使用Bagging可以综合投票结果，从而提升稳定性以及准确率
4.便于并行化。多个抽样数据的获取及!型的训练互相没有关联，可以方便地进行并行计算

随机森林

最典型的Bagging算法：随机是其核心，森林意在说明它是通过组合多棵决策树来构建模型。
主要特点：对样本进行有放回抽样；对特征进行随机抽样；基本分类器最常见的为决策树
在市场营销、股票市场分析、金融欺诈检测、基因组数据分析和疾病风险预测等实际问题中得到了广泛应用。

算法原理

随机森林使用并汇总多棵决策树进行预测，所以即使每棵树的决策能力很弱，由它们组合起来形成的随机森林的决策能力也会较强。
假设使用三棵决策树组合成随机森林，每棵树各不相同且预测结果相互独立，每棵树的预测错误率为40%，那么两棵树以及两棵树以上预测错误的概率下降为三棵全部错误+两棵树错误一棵树正确=0.46³+30.4²(1-0.4)=0.352，降低了错误率。
在上述过程中，需要注意一点的是，错误率降低的前提假设：每棵树各不相同且预测结果相互独立。随机森林在构建每棵树的时候，为了保证各棵树之间的独立性，通常会采用两到三层的随机性：随机有放回的抽取样本、随机选取m个特征、随机选择特征取值进行分割（不遍历特征所有取值）

m值的选取：大的m值可以使得决策树的准确率提高，但是多棵决策树之间的相关性却很高。方法一：交叉验证方法选取最佳m值，方法二：经验设置，通常选取m=log₂d+1,其中d为特征维度

随机森林的性能评估

分类间隔：正确分类某样本的决策树的比例减去错误分类样本决策树的比例。假设对样本A有75%的树分类正确，那么分类间隔就是75%-25%=50%。通过平均随机森林在各个样本上的分类间隔得到随机森林的分类间隔。实际上，我们希望分类间隔越大越好，因为大的分类间隔表示我们的分类效果比较稳定，泛化效果更好。

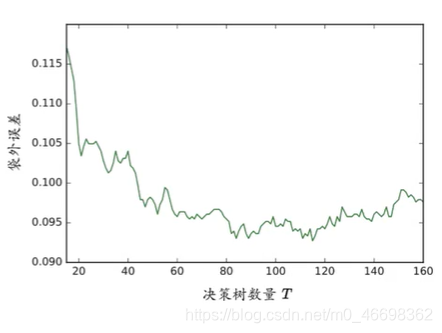
袋外误差：随机森林对袋外样本的预测错误率。
袋外样本：对于一棵树而言，没有被抽样到训练集中的样本。
计算方式：对每个样本，计算把该样本作为袋外样本的树对该样本的分类情况；以简单多数投票作为该样本的分类结果；以误分样本个数占样本总数的比率作为随机森林的袋外误差

随机森林与特征选择

随机森林能够给出特征的重要性度量，帮助进行特征选择
1.计算特征的平均信息增益大小。
训练决策树时，可以算出每个特征在每棵树中有多大的信息增益，算出每个特征在随机森林中的平均信息增益，作为该特征的重要性。
2.计算每个特征对模型准确率的影响。
通过打乱样本中某一特征的特征值顺序，产生新样本。新样本放入建立好的随机森林模型计算准确率，对于重要的特征来说，打乱顺序会极大的降低模型的准确率。

算法分析

假设单棵决策树的方差为σ²(x)，任意两颗决策树之间的相关性为p(x)，随机森林一共由T棵决策树组成，则集成的随机森林模型的方差var(x)为

优缺点

优点:
1.能够处理很高维度的数据，并且不用做特征选择
2.对特征之间存在的多重共线性不敏感，并且能够在一定程度上处理缺失数据和不均衡数据
3.在训练完后能够给出哪些特征比较重要
4.容易做成并行化方法

缺点:
1.处理噪音较大的小样本和低维数据集的问题上会过度拟合
2.相对于决策树，预测速度较慢
3.相对于决策树，模型可解释性较差

随机森林的其他功能

计算样本的相似度：
在建立随机森林的时候，记录样本两两之间出现在同一叶子节点的次数，生成相似性矩阵(proximity matrix);如果越多的出现在同一叶节点，说明这两个样本越相似;如果越少的出现在同一叶节点，说明两个样本差异越大。