利用Bi-LSTM实现基于光谱数据对数值进行预测-实战示例

0前言&简介：

本文为《RNN之：LSTM 长短期记忆模型-结构-理论详解-及实战（Matlab向）》的拓展示例，对于初学者而言，还请先阅读原文，增强理解。

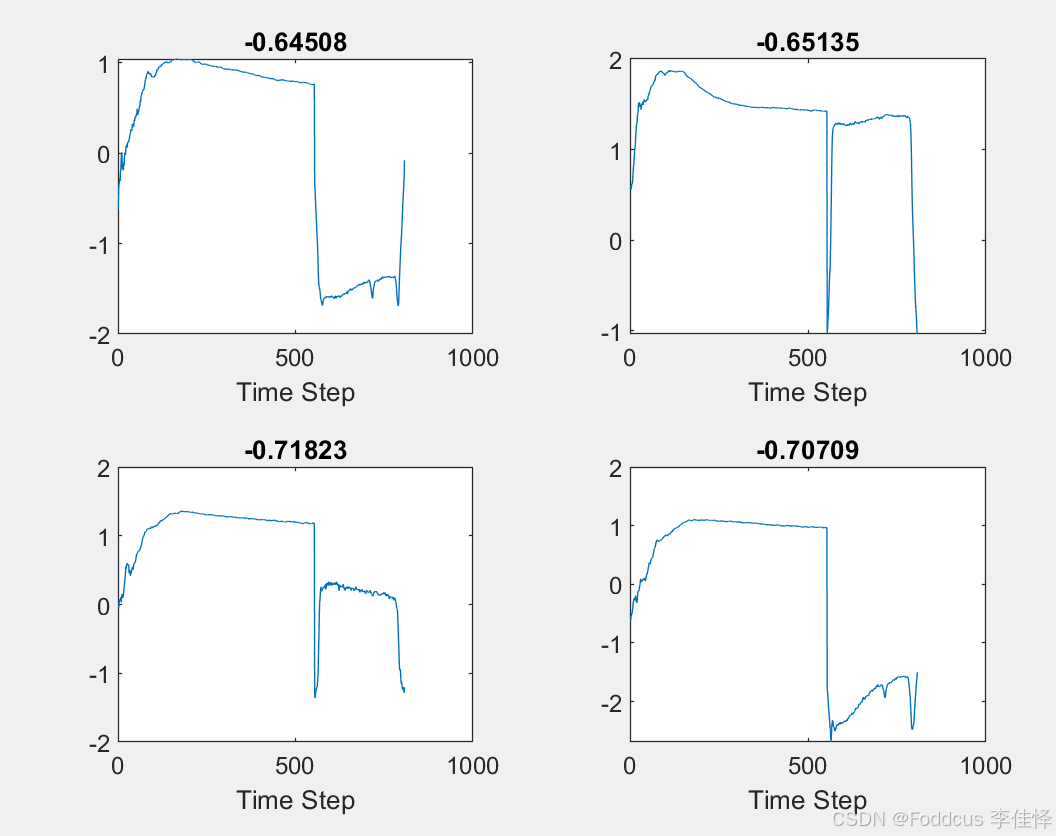
本示例采用了长度为807，样本数为129的光谱曲线数据，具体而言，在这篇示例中，光谱曲线经过了SNV标准化处理后，数据形态及其对应数值标签如下图所示。

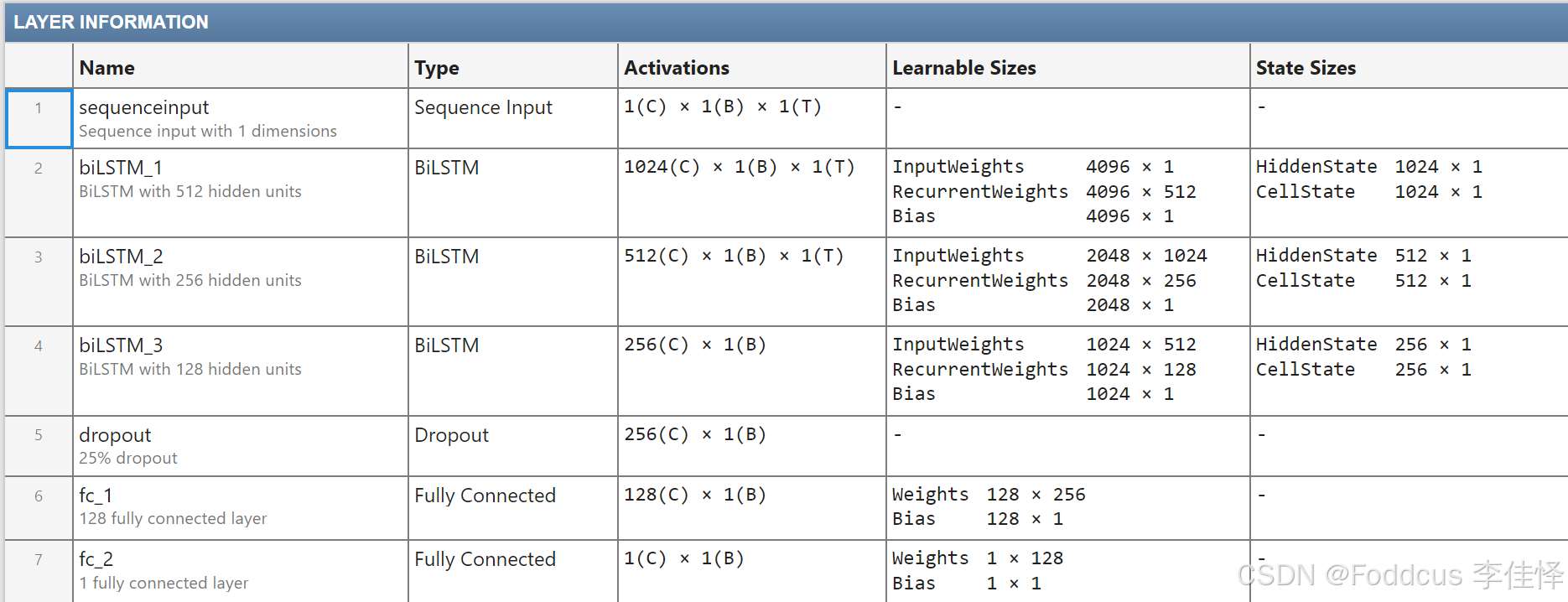
本实战示例设计的Bi-LSTM模型结构如下图所示，模型由三层Bi-LSTM层构成，隐藏单元数分别为1024、512和256，以及随机丢弃层和双层MLP，模型参数为5418241。由MLP直接输出数值。

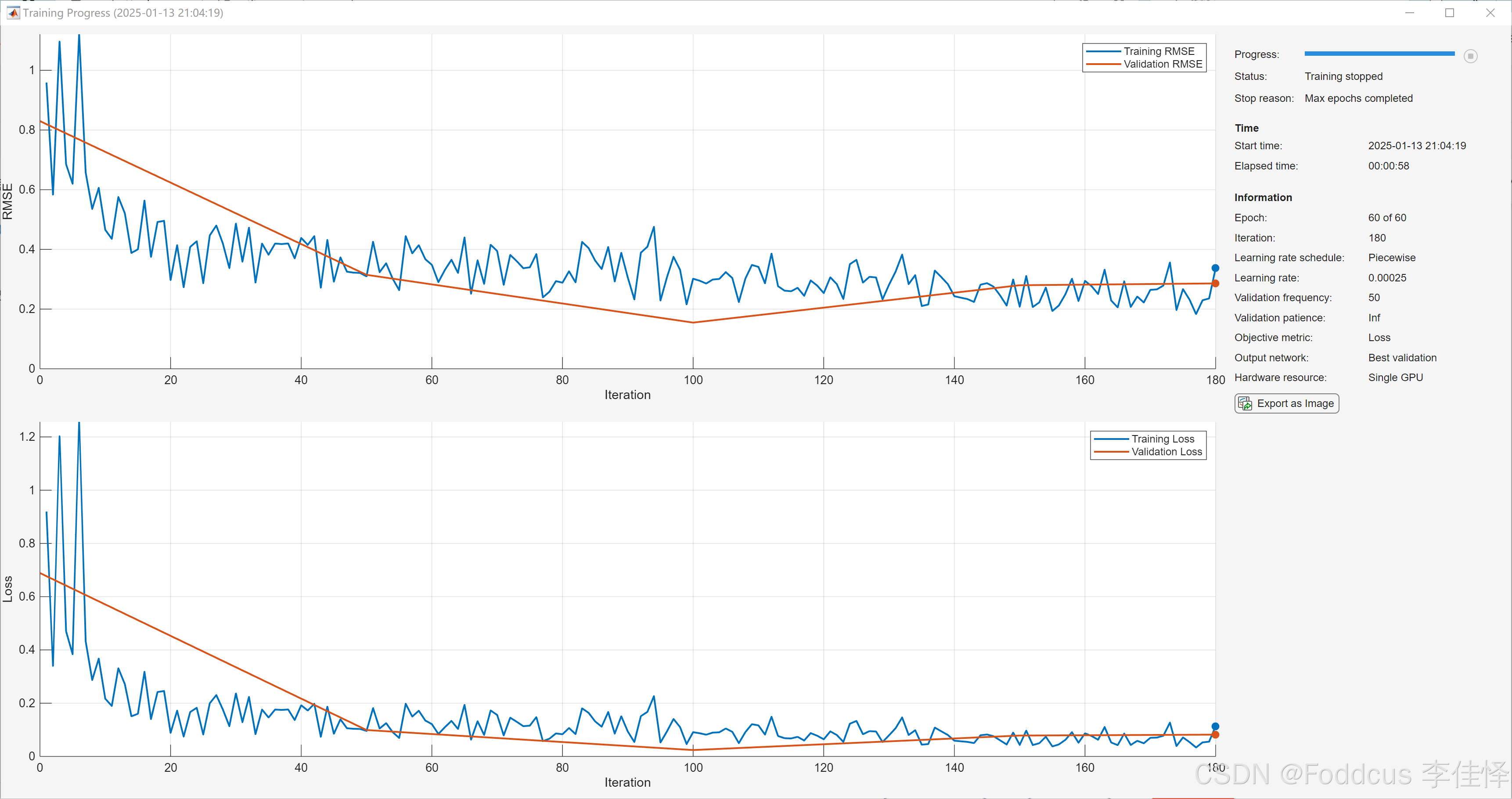
训练过程：

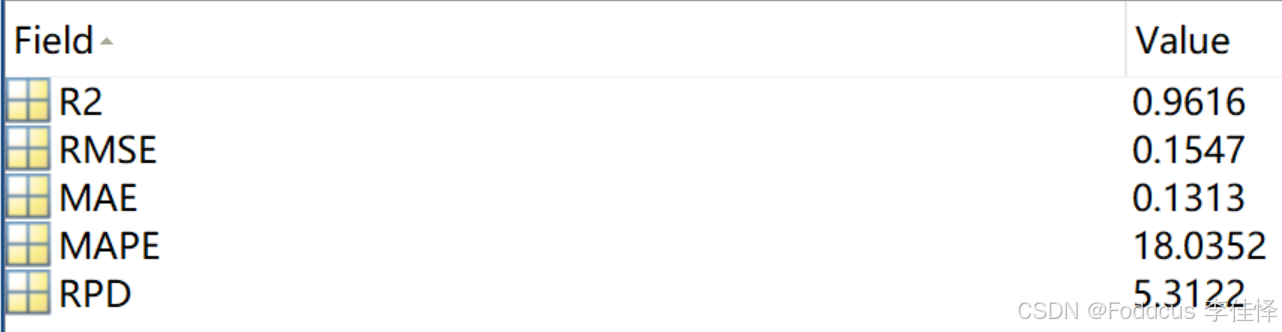
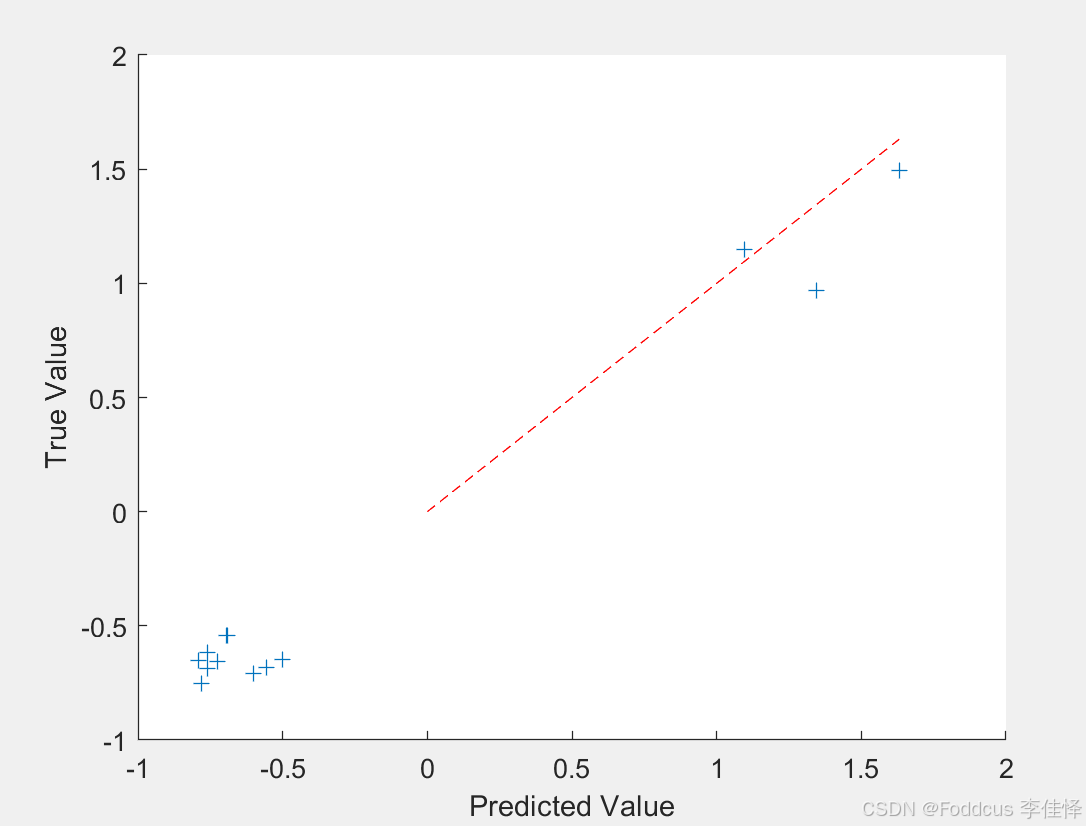
训练结果：

1.代码预览


%训练脚本示意：

clear variables
load Testdata.mat

%归一化
Data=normalize(Data);
PreditedValue=normalize(PreditedValue);

%展示数据
numChannels=1;
idx = [3 4 5 12];
figure
tiledlayout(2,2)

for i = 1:4
    nexttile
    plot(Data(idx(i),:))
    xlabel("Time Step")
    title(string(PreditedValue(idx(i))))
end


%预处理
numObservations = numel(Data(:,1));
[idxTrain,idxTest] = trainingPartitions(numObservations,[0.9 0.1]);
TData=Data(idxTrain,:);
TLable=PreditedValue(idxTrain);

VData=Data(idxTest,:);
VLable=PreditedValue(idxTest);

%对数据库进行预处理，转化为Cell储存的形式,cell代表样本，在cell中，行代表时间步，列代表通道
Sample_Num=size(VLable);
for i=1:Sample_Num
V_Data{i,1}=VData(i,:)';

end

Sample_Num=size(TLable);
for i=1:Sample_Num
T_Data{i,1}=TData(i,:)';
end

numHiddenUnits = 512;

layers = [
    sequenceInputLayer(1)
    bilstmLayer(numHiddenUnits,OutputMode='sequence')
    bilstmLayer(numHiddenUnits/2,OutputMode='sequence')
    bilstmLayer(numHiddenUnits/4,OutputMode='last')
    dropoutLayer(0.25)
    fullyConnectedLayer(128)
    fullyConnectedLayer(1)
    ]


options = trainingOptions("adam", ...
    MiniBatchSize=32,...
    MaxEpochs=60, ...
    InitialLearnRate=0.002,...
    GradientThreshold=1.5, ...
    Shuffle='every-epoch', ...%可以乱序，反正长度都一样
    Plots="training-progress", ...
    Metrics="rmse", ...
    Verbose=false,...
    ValidationData= {V_Data,VLable},...
    ValidationFrequency=50, ...
    LearnRateSchedule='piecewise',...%分段学习
    LearnRateDropFactor=0.5,...%学习率下降因子
    LearnRateDropPeriod=15);%下降周期间隔
     

%Train LSTM Neural Network
net = trainnet(T_Data,TLable,layers,"mse",options);

%Test LSTM Neural Network
%对测试数据进行分类，并计算预测的分类准确率。使用minibatchpredict函数进行预测
scores = minibatchpredict(net,V_Data);
metrics_t = analysisRegression_Detail(VLable, scores);

子函数：

function metrics = analysisRegression_Detail(actual, predicted)
% 确保输入是列向量  ,（N*2的矩阵，第一列是真实值）


% 计算残差
residuals = actual - predicted;

% 计算R²
SS_res = sum(residuals.^2);
SS_tot = sum((actual - mean(actual)).^2);
R2 = 1 - SS_res / SS_tot;

% 计算RMSE
RMSE = sqrt(mean(residuals.^2));

% 计算MAE
MAE = mean(abs(residuals));

% 计算MAPE
MAPE = mean(abs(residuals ./ actual)) * 100;

% 计算RPD
STD_actual = std(actual);
RPD = STD_actual / RMSE;

% 输出结果
metrics = struct('R2', R2, 'RMSE', RMSE, 'MAE', MAE, 'MAPE', MAPE, 'RPD', RPD);
%RMSE与MAE联合使用，可以看出样本误差的离散程度，若RMSE远大于MAE，则可以知道不同样本的误差差别很大
%MAE与MAPE，若MAE远大于MAPE*（y平均），则可能是模型对真实值小的样本预测更准，此时就可以考虑为不同数量级的样本建立不同的模型。
figure
scatter(predicted,actual,'+')
xlabel("Predicted Value")
ylabel("True Value")
% 计算R²
hold on
Maxnum=max(max(actual),max(predicted));
plot([0 Maxnum], [0 Maxnum],'r--')

end

2.原数据、代码及注意事项

代码&数据下载：24-BiLSTM_Regression.zip
链接: https://pan.baidu.com/s/1J4tURXk4KQd2MGMWV5a9Aw?pwd=vue8 提取码: vue8

关于输出

基本需要注意的问题在详解中已经充分说明了，即前最后一个Bi-LSTM层要用“最后状态输出”（否者输出不匹配），并且前两层Bi-LSTM层要用“序列状态”输出（否者无法堆叠）。

输出不使用sigmoid激活函数的原因是预测标签的分布超过了[0~1]的范围，sigmoid无法精确映射，使用该该激活函数会严重训练。不过也可以在训练前让标签映射至0~1范围内，再通过sigmoid激活函数增加训练稳定性。

关于训练设置

在该示例中，GradientThreshold被设置为1.5，而通常梯度阈值默认设置为1.

这是因为，在RNN的训练中，由于权重在时间维度上共享，因此梯度会沿着时间轴累积，容易造成梯度爆炸。所以在训练LSTM的过程中，一般会使用较大的梯度阈值（一般也不会超过2），读者在实际应用中，可以多次尝试对GradientThreshold进行调制。