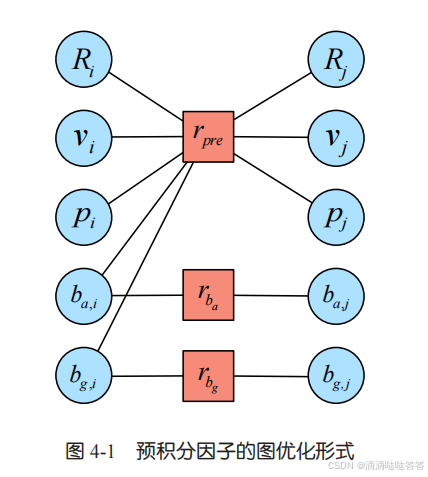
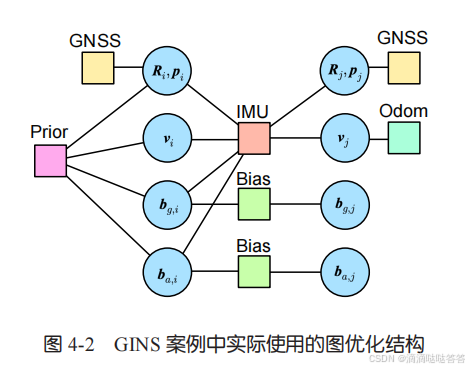
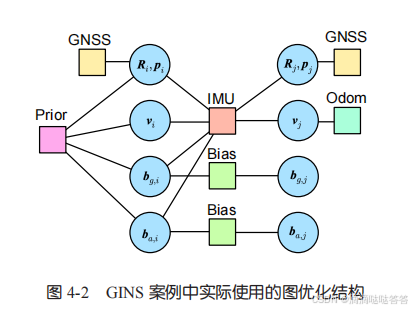
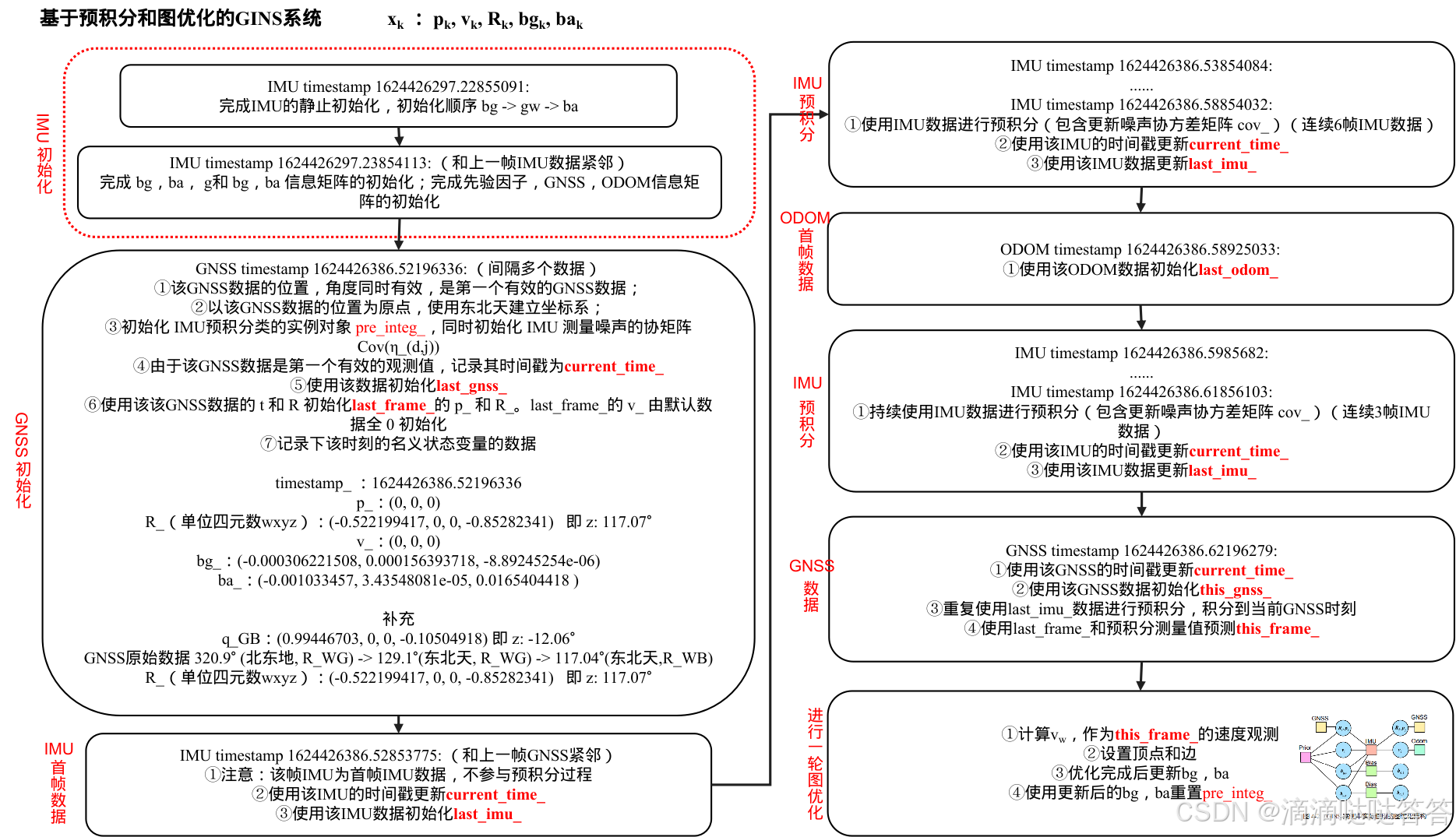
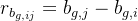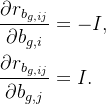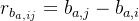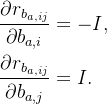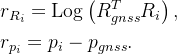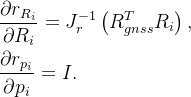《自动驾驶与机器人中的SLAM技术》ch4：基于预积分和图优化的 GINS

前言：预积分图优化的结构

1 预积分的图优化顶点

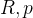
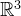
这里使用《自动驾驶与机器人中的SLAM技术》ch4：预积分学中提到的散装的形式来实现预积分的顶点部分，所以每个状态被分为位姿（ R,p ）、速度、陀螺零偏、加计零偏四种顶点（共 15 维）。后三者实际上都是 $\mathbb{R}^3$ 的变量，可以直接使用继承来实现。g2o 部分可参考 G2O (General Graph Optimization) 。

下文中提到的顶点的维度为优化变量的维度。

1.1 旋转在前，平移在后的位姿顶点（6维）

位姿顶点的顺序为旋转在前，平移在后，雅可比矩阵的顺序要与之对应。

/**
 * 旋转在前，平移在后的的SO3+t类型pose，6自由度，存储时伪装为g2o::VertexSE3，供g2o_viewer查看
 */
class VertexPose : public g2o::BaseVertex<6, SE3> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    VertexPose() {}

    // 读写函数是为了保存顶点信息到 .g2o 文件中的，该文件可使用 g2o_viewer 可视化
    bool read(std::istream& is) override {
        double data[7];
        for (int i = 0; i < 7; i++) {
            is >> data[i];
        }
        setEstimate(SE3(Quatd(data[6], data[3], data[4], data[5]), Vec3d(data[0], data[1], data[2])));
        return true;
    }

    bool write(std::ostream& os) const override {
        os << "VERTEX_SE3:QUAT ";
        os << id() << " ";
        Quatd q = _estimate.unit_quaternion();
        os << _estimate.translation().transpose() << " ";
        os << q.coeffs()[0] << " " << q.coeffs()[1] << " " << q.coeffs()[2] << " " << q.coeffs()[3] << std::endl;
        return true;
    }

    // 重置。这里未实现该函数的功能
    virtual void setToOriginImpl() {}

    // 更新
    virtual void oplusImpl(const double* update_) {
        // Eigen::Map<const Vec3d>(&update_[0]) ：使用 &update_[0] 获取指向数组中第 1 个元素的地址，从该地址开始，将 update_ 数组连续的 3 个元素映射为一个 Eigen::Vector3d 对象
        // Eigen::Map<const Vec3d>(&update_[3]) ：使用 &update_[3] 获取指向数组中第 4 个元素的地址，从该地址开始，将 update_ 数组连续的 3 个元素映射为一个 Eigen::Vector3d 对象
        // Eigen::Map: 这是一个模板类，用于将现有的内存块映射为 Eigen 对象。这种映射是零开销的，因为它不会复制数据，而是直接使用提供的内存。
        _estimate.so3() = _estimate.so3() * SO3::exp(Eigen::Map<const Vec3d>(&update_[0]));  // 旋转部分，右乘更新
        _estimate.translation() += Eigen::Map<const Vec3d>(&update_[3]);                     // 平移部分
        updateCache();
    }
};

1.2 速度顶点（3维）

/**
 * 速度顶点，单纯的Vec3d
 */
class VertexVelocity : public g2o::BaseVertex<3, Vec3d> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    VertexVelocity() {}

    virtual bool read(std::istream& is) { return false; }
    virtual bool write(std::ostream& os) const { return false; }

    virtual void setToOriginImpl() { _estimate.setZero(); }

    virtual void oplusImpl(const double* update_) { _estimate += Eigen::Map<const Vec3d>(update_); }
};

1.3 陀螺仪和加速度计零偏顶点（3维）

陀螺仪零偏顶点和加速度计零偏顶点均继承自速度顶点。

/**
 * 陀螺零偏顶点，亦为Vec3d，从速度顶点继承
 */
class VertexGyroBias : public VertexVelocity {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    VertexGyroBias() {}
};

/**
 * 加计零偏顶点，Vec3d，亦从速度顶点继承
 */
class VertexAccBias : public VertexVelocity {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    VertexAccBias() {}
};

2 预积分的图优化边

在基于预积分和图优化的 GINS 系统中，边主要有以下几种：

1. 预积分的边，约束上一时刻的 15 维状态与下一时刻的旋转、平移、速度；
2. 零偏随机游走的边，共两种，连接两个时刻的零偏状态；
3. GNSS 的观测边。因为我们使用六自由度观测，所以它关联单个时刻的位姿；
4. 先验信息，刻画上一时刻的状态分布，关联下一时刻的 15 维状态；
5. 轮速计的观测边。关联上一时刻的速度顶点。

下文中提到的边的维度为 观测值维度 。

2.1 预积分边（9维多元边）

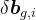
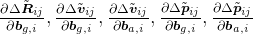
注意：预积分边需要从外部传入预积分对象、重力矢量和权重因子（为信息矩阵添加的乘积因子）。其中需要从预积分类中获取整体预积分时间、预积分的协方差矩阵（其逆乘以权重因子作为信息矩阵）、预积分陀螺仪零偏（计算 $\delta\boldsymbol{b}_{g,i}$ ）、雅可比矩阵（ $\frac{\partial\Delta\tilde{\boldsymbol{R}}_{ij}}{\partial\boldsymbol{b}_{g,i}}, \frac{\partial\Delta\tilde{\boldsymbol{v}}_{ij}}{\partial\boldsymbol{b}_{g,i}}, \frac{\partial\Delta\tilde{\boldsymbol{v}}_{ij}}{\partial\boldsymbol{b}_{a,i}}, \frac{\partial\Delta\tilde{\boldsymbol{p}}_{ij}}{\partial\boldsymbol{b}_{g,i}}, \frac{\partial\Delta\tilde{\boldsymbol{p}}_{ij}}{\partial\boldsymbol{b}_{a,i}}$ ）和零偏更新时修正后的预积分观测量。

其中残差的定义及残差对状态变量的雅可比矩阵见《自动驾驶与机器人中的SLAM技术》ch4：预积分学中的推导。

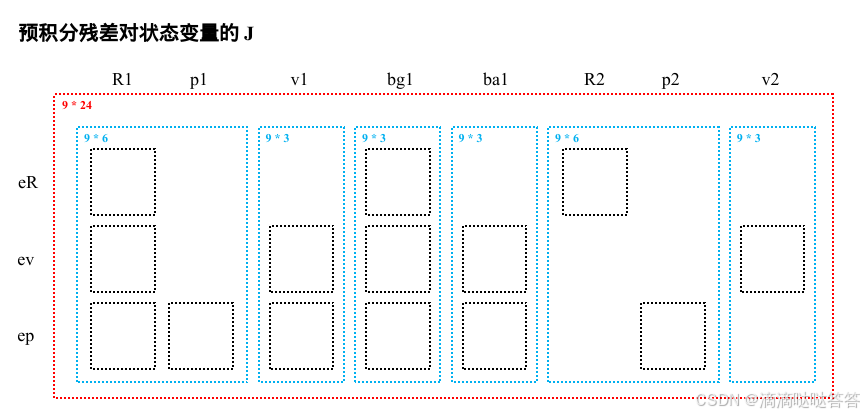
计算预积分残差对状态变量的雅可比矩阵的结构如下图所示：

代码实现如下：

/// 与预积分相关的vertex, edge
/**
 * 预积分边（多元边）
 * 连接6个顶点：上一帧的pose, v, bg, ba，下一帧的pose, v
 * 观测量为9维，即预积分残差, 顺序：R, v, p
 * information从预积分类中获取，构造函数中计算
 * 旋转在前，平移在后
 */
class EdgeInertial : public g2o::BaseMultiEdge<9, Vec9d> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    /**
     * 构造函数中需要指定预积分类对象
     * @param preinteg  预积分对象指针
     * @param gravity   重力矢量
     * @param weight    权重。为信息矩阵添加的乘积因子
     */
    EdgeInertial(std::shared_ptr<IMUPreintegration> preinteg, const Vec3d& gravity, double weight = 1.0);

    bool read(std::istream& is) override { return false; }
    bool write(std::ostream& os) const override { return false; }

    // 计算边的误差，即预积分残差
    void computeError() override;
    // 计算雅可比矩阵
    void linearizeOplus() override;

    // 计算 Hessian 矩阵
    Eigen::Matrix<double, 24, 24> GetHessian() {
        linearizeOplus();
        Eigen::Matrix<double, 9, 24> J;
        J.block<9, 6>(0, 0) = _jacobianOplus[0];
        J.block<9, 3>(0, 6) = _jacobianOplus[1];
        J.block<9, 3>(0, 9) = _jacobianOplus[2];
        J.block<9, 3>(0, 12) = _jacobianOplus[3];
        J.block<9, 6>(0, 15) = _jacobianOplus[4];
        J.block<9, 3>(0, 21) = _jacobianOplus[5];
        return J.transpose() * information() * J;
    }

   private:
    const double dt_;
    std::shared_ptr<IMUPreintegration> preint_ = nullptr;
    Vec3d grav_;
};

EdgeInertial::EdgeInertial(std::shared_ptr<IMUPreintegration> preinteg, const Vec3d& gravity, double weight)
    : preint_(preinteg), dt_(preinteg->dt_) {
    resize(6);  // 6个关联顶点
    grav_ = gravity;
    setInformation(preinteg->cov_.inverse() * weight);
}

void EdgeInertial::computeError() {
    auto* p1 = dynamic_cast<const VertexPose*>(_vertices[0]);
    auto* v1 = dynamic_cast<const VertexVelocity*>(_vertices[1]);
    auto* bg1 = dynamic_cast<const VertexGyroBias*>(_vertices[2]);
    auto* ba1 = dynamic_cast<const VertexAccBias*>(_vertices[3]);
    auto* p2 = dynamic_cast<const VertexPose*>(_vertices[4]);
    auto* v2 = dynamic_cast<const VertexVelocity*>(_vertices[5]);

    Vec3d bg = bg1->estimate();
    Vec3d ba = ba1->estimate();

    // 零偏的更新（假设预积分的测量值是随零偏线性变化的，当零偏更新时，在原先预积分测量值的基础上进行修正得到新的预积分测量值）
    const SO3 dR = preint_->GetDeltaRotation(bg);
    const Vec3d dv = preint_->GetDeltaVelocity(bg, ba);
    const Vec3d dp = preint_->GetDeltaPosition(bg, ba);

    /// 预积分误差项 p112 （4.41）
    // 预积分残差项
    const Vec3d er = (dR.inverse() * p1->estimate().so3().inverse() * p2->estimate().so3()).log();
    Mat3d RiT = p1->estimate().so3().inverse().matrix();
    const Vec3d ev = RiT * (v2->estimate() - v1->estimate() - grav_ * dt_) - dv;
    const Vec3d ep = RiT * (p2->estimate().translation() - p1->estimate().translation() - v1->estimate() * dt_ -
                            grav_ * dt_ * dt_ / 2) -
                     dp;
    _error << er, ev, ep;
}

void EdgeInertial::linearizeOplus() {
    // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
    // 顺序为 v0_pose、v0_vel、v0_bg、v0_ba、v1_pose、v1_vel（这里体现了 旋转在前，平移在后）
    auto* p1 = dynamic_cast<const VertexPose*>(_vertices[0]);
    auto* v1 = dynamic_cast<const VertexVelocity*>(_vertices[1]);
    auto* bg1 = dynamic_cast<const VertexGyroBias*>(_vertices[2]);
    auto* ba1 = dynamic_cast<const VertexAccBias*>(_vertices[3]);
    auto* p2 = dynamic_cast<const VertexPose*>(_vertices[4]);
    auto* v2 = dynamic_cast<const VertexVelocity*>(_vertices[5]);

    Vec3d bg = bg1->estimate();
    Vec3d ba = ba1->estimate();
    Vec3d dbg = bg - preint_->bg_;

    // 一些中间符号
    const SO3 R1 = p1->estimate().so3();
    const SO3 R1T = R1.inverse();
    const SO3 R2 = p2->estimate().so3();

    auto dR_dbg = preint_->dR_dbg_;
    auto dv_dbg = preint_->dV_dbg_;
    auto dp_dbg = preint_->dP_dbg_;
    auto dv_dba = preint_->dV_dba_;
    auto dp_dba = preint_->dP_dba_;

    // 估计值
    Vec3d vi = v1->estimate();
    Vec3d vj = v2->estimate();
    Vec3d pi = p1->estimate().translation();
    Vec3d pj = p2->estimate().translation();

    const SO3 dR = preint_->GetDeltaRotation(bg);
    const SO3 eR = SO3(dR).inverse() * R1T * R2;
    const Vec3d er = eR.log();
    // 修复 bug 
    const Mat3d invJr = SO3::jr_inv(er);

    /// 雅可比矩阵
    /// 注意有3个index, 顶点的，自己误差的，顶点内部变量的
    /// 变量顺序：pose1(R1,p1), v1, bg1, ba1, pose2(R2,p2), v2
    /// 残差顺序：eR, ev, ep，残差顺序为行(row)，变量顺序为列(col)

    //       | R1 | p1 | v1 | bg1 | ba1 | R2 | p2 | v2 |
    //  vert | 0       | 1  | 2   | 3   | 4       | 5  |
    //  col  | 0    3  | 0  | 0   | 0   | 0    3  | 0  |
    //    row
    //  eR 0 |
    //  ev 3 |
    //  ep 6 |

    /// 残差对R1, 9x3
    _jacobianOplus[0].setZero();
    // dR/dR1, p113 (4.42)
    _jacobianOplus[0].block<3, 3>(0, 0) = -invJr * (R2.inverse() * R1).matrix();
    // dv/dR1, p115 (4.47)
    _jacobianOplus[0].block<3, 3>(3, 0) = SO3::hat(R1T * (vj - vi - grav_ * dt_));
    // dp/dR1, p115 (4.48d）
    _jacobianOplus[0].block<3, 3>(6, 0) = SO3::hat(R1T * (pj - pi - vi * dt_ - 0.5 * grav_ * dt_ * dt_));

    /// 残差对p1, 9x3
    // dp/dp1, p115 (4.48a)
    _jacobianOplus[0].block<3, 3>(6, 3) = -R1T.matrix();

    /// 残差对v1, 9x3
    _jacobianOplus[1].setZero();
    // dv/dv1, p114 (4.46a)
    _jacobianOplus[1].block<3, 3>(3, 0) = -R1T.matrix();
    // dp/dv1, p115 (4.48c)
    _jacobianOplus[1].block<3, 3>(6, 0) = -R1T.matrix() * dt_;

    /// 残差对bg1
    _jacobianOplus[2].setZero();
    // dR/dbg1, p114 (4.45)
    _jacobianOplus[2].block<3, 3>(0, 0) = -invJr * eR.inverse().matrix() * SO3::jr((dR_dbg * dbg).eval()) * dR_dbg;
    // dv/dbg1  p111 (4.38)前添加负号
    _jacobianOplus[2].block<3, 3>(3, 0) = -dv_dbg;
    // dp/dbg1  p111 (4.38)前添加负号
    _jacobianOplus[2].block<3, 3>(6, 0) = -dp_dbg;

    /// 残差对ba1
    _jacobianOplus[3].setZero();
    // dv/dba1  p111 (4.38)前添加负号
    _jacobianOplus[3].block<3, 3>(3, 0) = -dv_dba;
    // dp/dba1  p111 (4.38)前添加负号
    _jacobianOplus[3].block<3, 3>(6, 0) = -dp_dba;

    /// 残差对pose2
    _jacobianOplus[4].setZero();
    // dr/dr2, p114 (4.43)
    _jacobianOplus[4].block<3, 3>(0, 0) = invJr;
    // dp/dp2, p115 (4.48b)
    _jacobianOplus[4].block<3, 3>(6, 3) = R1T.matrix();

    /// 残差对v2
    _jacobianOplus[5].setZero();
    // dv/dv2, p114 (4,46b)
    _jacobianOplus[5].block<3, 3>(3, 0) = R1T.matrix();  // OK
}

2.2 零偏随机游走边（3维双元边）

2.2.1 陀螺仪随机游走边

残差定义：

$r_{ b_{g,ij}}=b_{g,j}-b_{g,i}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ b_{g,ij}}}{\partial b_{g,i}}=-I, \\ & \frac{\partial r_{ b_{g,ij}}}{\partial b_{g,j}}=I . \end{aligned}$

/**
 * 陀螺仪随机游走边（双元边）
 */
class EdgeGyroRW : public g2o::BaseBinaryEdge<3, Vec3d, VertexGyroBias, VertexGyroBias> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    EdgeGyroRW() {}

    virtual bool read(std::istream& is) { return false; }
    virtual bool write(std::ostream& os) const { return false; }

    void computeError() {
        // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
        // 顺序为 v0_bg、v1_bg
        const auto* VG1 = dynamic_cast<const VertexGyroBias*>(_vertices[0]);
        const auto* VG2 = dynamic_cast<const VertexGyroBias*>(_vertices[1]);
        _error = VG2->estimate() - VG1->estimate();
    }

    virtual void linearizeOplus() {
        // 残差对 bg1, 3x3
        _jacobianOplusXi = -Mat3d::Identity();
        // 残差对 bg2, 3x3
        _jacobianOplusXj.setIdentity();
    }

    Eigen::Matrix<double, 6, 6> GetHessian() {
        linearizeOplus();
        Eigen::Matrix<double, 3, 6> J;
        J.block<3, 3>(0, 0) = _jacobianOplusXi;
        J.block<3, 3>(0, 3) = _jacobianOplusXj;
        return J.transpose() * information() * J;
    }
};

2.2.2 加速度计随机游走边

残差定义：

$r_{ b_{a,ij}}=b_{a,j}-b_{a,i}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ b_{a,ij}}}{\partial b_{a,i}}=-I, \\ & \frac{\partial r_{ b_{a,ij}}}{\partial b_{a,j}}=I . \end{aligned}$

/**
 * 加速度计随机游走边（双元边）
 */
class EdgeAccRW : public g2o::BaseBinaryEdge<3, Vec3d, VertexAccBias, VertexAccBias> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    EdgeAccRW() {}

    virtual bool read(std::istream& is) { return false; }
    virtual bool write(std::ostream& os) const { return false; }

    void computeError() {
        // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
        // 顺序为 v0_ba、v1_ba
        const auto* VA1 = dynamic_cast<const VertexAccBias*>(_vertices[0]);
        const auto* VA2 = dynamic_cast<const VertexAccBias*>(_vertices[1]);
        _error = VA2->estimate() - VA1->estimate();
    }

    virtual void linearizeOplus() {
        // 残差对 ba1, 3x3
        _jacobianOplusXi = -Mat3d::Identity();
        // 残差对 ba2, 3x3
        _jacobianOplusXj.setIdentity();
    }

    Eigen::Matrix<double, 6, 6> GetHessian() {
        linearizeOplus();
        Eigen::Matrix<double, 3, 6> J;
        J.block<3, 3>(0, 0) = _jacobianOplusXi;
        J.block<3, 3>(0, 3) = _jacobianOplusXj;
        return J.transpose() * information() * J;
    }
};

2.3 GNSS 观测边（单边）

GNSS 方案分为双天线方案和单天线方案。

2.3.1 双天线方案（6维旋转+位移）

注意：双天线 GNSS 边需要从外部传入 GNSS 测量值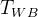（ $T_{WB}$ ）。

残差定义：

$\begin{aligned} & r_{ R_{i}}=\mathrm{Log}\left(R_{gnss}^{T}R_{i}\right), \\&r_{ p_{i}}=p_{i}-p_{gnss}. \end{aligned}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ R_{i}}}{\partial R_{i}}=J_r^{-1}\left({ R_{gnss}^{T}R_{i}}\right), \\ &\frac{\partial r_{ p_{i}}}{\partial p_{i}}=I. \end{aligned}$

时刻的 GNSS 残差和雅可比矩阵同上。

/**
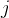
 * 6 自由度的GNSS
 * 误差的旋转在前，平移在后
 */
class EdgeGNSS : public g2o::BaseUnaryEdge<6, SE3, VertexPose> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    EdgeGNSS() = default;
    EdgeGNSS(VertexPose* v, const SE3& obs) {
        setVertex(0, v);
        setMeasurement(obs);
    }
    // 这里使用的是 bag包或者 .txt数据，其中的 GNSS 数据已经被转换到车体坐标系下了，是直接对 R,p 的观测
    void computeError() override {
        // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
        // 顺序为 p_gnss_0 或者 p_gnss_1
        VertexPose* v = (VertexPose*)_vertices[0];
        _error.head<3>() = (_measurement.so3().inverse() * v->estimate().so3()).log();
        _error.tail<3>() = v->estimate().translation() - _measurement.translation();
    };

    void linearizeOplus() override {
        VertexPose* v = (VertexPose*)_vertices[0];
        // jacobian 6x6
        _jacobianOplusXi.setZero();
        _jacobianOplusXi.block<3, 3>(0, 0) = (_measurement.so3().inverse() * v->estimate().so3()).jr_inv();  // dR/dR
        _jacobianOplusXi.block<3, 3>(3, 3) = Mat3d::Identity();                                              // dp/dp
    }

    Mat6d GetHessian() {
        linearizeOplus();
        return _jacobianOplusXi.transpose() * information() * _jacobianOplusXi;
    }

    virtual bool read(std::istream& in) { return true; }
    virtual bool write(std::ostream& out) const { return true; }

   private:
};

2.3.2 单天线方案（3维位移）

注意：单天线 GNSS 边需要从外部传入传感器外参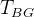（ $T_{BG}$ ）和 GNSS 测量值（此时是 $T_{WG}$ 而不是双天线的 $T_{WB}$ ）。

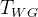
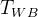
残差定义：

$\begin{aligned} &r_{ p_{i}}=p_{i}*T_{BG}-p_{gnss}. \end{aligned}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ p_{i}}}{\partial p_{i}}=I. \end{aligned}$

时刻的 GNSS 残差和雅可比矩阵同上。

/**
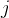
 * 只有平移的GNSS
 * 此时需要提供RTK外参 TBG，才能正确施加约束
 */
class EdgeGNSSTransOnly : public g2o::BaseUnaryEdge<3, Vec3d, VertexPose> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    /**
     * 指定位姿顶点、RTK观测 t_WG、外参TGB
     * @param v
     * @param obs
     */
    EdgeGNSSTransOnly(VertexPose* v, const Vec3d& obs, const SE3& TBG) : TBG_(TBG) {
        setVertex(0, v);
        setMeasurement(obs);
    }

    void computeError() override {
        // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
        // 顺序为 p_gnss_0 或者 p_gnss_1
        VertexPose* v = (VertexPose*)_vertices[0];
        // RTK 读数为 T_WG
        _error = (v->estimate() * TBG_).translation() - _measurement;
    };

    // 可以由用户提供雅可比矩阵的解析解；或者省略 linearizeOplus() 函数使用 g2o 默认的数值方式自动计算雅可比矩阵的数值解，但效率较低并且可能会引入误差
    // void linearizeOplus() override {
    //     VertexPose* v = (VertexPose*)_vertices[0];
    //     // jacobian 6x6
    //     _jacobianOplusXi.setZero();
    //     _jacobianOplusXi.block<3, 3>(0, 0) = (_measurement.so3().inverse() * v->estimate().so3()).jr_inv();  // dR/dR
    //     _jacobianOplusXi.block<3, 3>(3, 3) = Mat3d::Identity();                                              // dp/dp
    // }

    virtual bool read(std::istream& in) { return true; }
    virtual bool write(std::ostream& out) const { return true; }

   private:
    SE3 TBG_;
};

2.4 先验因子边（15维多元边）

注意：先验信息边需要从外部传入 上一轮优化（ i-n 时刻到时刻）得到的时刻关键帧状态（ R,p,v,b_g,b_a ，这里加上下标 $last\underline{~}state$ 区分）和先验信息矩阵（上一轮优化完成后，利用边缘化（对 Hessian 矩阵）的方法，求出的时刻关键帧状态的协方差矩阵，作为当前轮优化时时刻状态的先验因子使用）。

残差定义：

$\begin{aligned} & r_{ R_{i}}=\mathrm{Log}\left(R_{last\underline{~}state}^{T}R_{i}\right), \\&r_{ p_{i}}=p_{i}-p_{last\underline{~}state}, \\&r_{ v_{i}}=v_{i}-v_{last\underline{~}state}, \\& r_{ b_{g,i}}=b_{g,i}-b_{g,last\underline{~}state}, \\& r_{ b_{a,i}}=b_{a,i}-b_{a,last\underline{~}state}. \end{aligned}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ R_{i}}}{\partial R_{i}}=J_r^{-1}(r_{ R_{i}}), \\ &\frac{\partial r_{ p_{i}}}{\partial p_{i}}=I, \\ &\frac{\partial r_{ v_{i}}}{\partial v_{i}}=I, \\ &\frac{\partial r_{ b_{g,i}}}{\partial b_{g,i}}=I, \\ & \frac{\partial r_{ b_{a,i}}}{\partial b_{a,i}}=I . \end{aligned}$

/**
 * 先验信息边（多元变）
 * 对上一帧IMU pvq bias的先验
 * info 由外部指定，通过时间窗口边缘化给出
 *
 * 顶点顺序：pose, v, bg, ba
 * 残差顺序：R, p, v, bg, ba，15维
 * 残差的旋转在前，平移在后
 */
class EdgePriorPoseNavState : public g2o::BaseMultiEdge<15, Vec15d> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    EdgePriorPoseNavState(const NavStated& state, const Mat15d& info);

    virtual bool read(std::istream& is) { return false; }
    virtual bool write(std::ostream& os) const { return false; }

    void computeError();
    virtual void linearizeOplus();

    Eigen::Matrix<double, 15, 15> GetHessian() {
        linearizeOplus();
        Eigen::Matrix<double, 15, 15> J;
        J.block<15, 6>(0, 0) = _jacobianOplus[0];
        J.block<15, 3>(0, 6) = _jacobianOplus[1];
        J.block<15, 3>(0, 9) = _jacobianOplus[2];
        J.block<15, 3>(0, 12) = _jacobianOplus[3];
        return J.transpose() * information() * J;
    }

    NavStated state_;
};

EdgePriorPoseNavState::EdgePriorPoseNavState(const NavStated& state, const Mat15d& info) {
    resize(4);
    state_ = state;
    setInformation(info);
}

void EdgePriorPoseNavState::computeError() {
    // 在 setVertex() 函数中设置 void setVertex(size_t i, Vertex* v) {_vertices[i]=v;}
    // 顺序为 v0_pose、v0_vel、v0_bg、v0_ba
    auto* vp = dynamic_cast<const VertexPose*>(_vertices[0]);
    auto* vv = dynamic_cast<const VertexVelocity*>(_vertices[1]);
    auto* vg = dynamic_cast<const VertexGyroBias*>(_vertices[2]);
    auto* va = dynamic_cast<const VertexAccBias*>(_vertices[3]);

    const Vec3d er = SO3(state_.R_.matrix().transpose() * vp->estimate().so3().matrix()).log();
    const Vec3d ep = vp->estimate().translation() - state_.p_;
    const Vec3d ev = vv->estimate() - state_.v_;
    const Vec3d ebg = vg->estimate() - state_.bg_;
    const Vec3d eba = va->estimate() - state_.ba_;

    _error << er, ep, ev, ebg, eba;
}

void EdgePriorPoseNavState::linearizeOplus() {
    const auto* vp = dynamic_cast<const VertexPose*>(_vertices[0]);
    const Vec3d er = SO3(state_.R_.matrix().transpose() * vp->estimate().so3().matrix()).log();

    //       | R1 | p1 | v1 | bg1 | ba1 |
    //  vert | 0       | 1  | 2   | 3   |
    //  col  | 0    3  | 0  | 0   | 0   |
    //    row
    //  eR 0 |
    //  ep 3 |
    //  ev 6 |
    // ebg 9 |
    // eba 12|

    /// 注意有3个index, 顶点的，自己误差的，顶点内部变量的
    _jacobianOplus[0].setZero();
    _jacobianOplus[0].block<3, 3>(0, 0) = SO3::jr_inv(er);    // dr/dr
    _jacobianOplus[0].block<3, 3>(3, 3) = Mat3d::Identity();  // dp/dp
    _jacobianOplus[1].setZero();
    _jacobianOplus[1].block<3, 3>(6, 0) = Mat3d::Identity();  // dv/dv
    _jacobianOplus[2].setZero();
    _jacobianOplus[2].block<3, 3>(9, 0) = Mat3d::Identity();  // dbg/dbg
    _jacobianOplus[3].setZero();
    _jacobianOplus[3].block<3, 3>(12, 0) = Mat3d::Identity();  // dba/dba
}

2.5 轮速计边（3维单元边）

注意：轮速计边需要从外部传入经过转换后的 $v_{odom}$ （世界坐标系下），ODOM 观测的是车体坐标系下的车头朝向的速度 $v_{b,x}$ 。

残差定义：

$\begin{aligned} &r_{ v_{j}}=v_{j}*-v_{odom}. \end{aligned}$

残差对状态变量的雅可比矩阵：

$\begin{aligned} & \frac{\partial r_{ v_{j}}}{\partial v_{j}}=I. \end{aligned}$

/**
 * 3维 轮速计观测边
 * 轮速观测世界速度在自车坐标系下矢量, 3维情况下假设自车不会有y和z方向速度
 */
class EdgeEncoder3D : public g2o::BaseUnaryEdge<3, Vec3d, VertexVelocity> {
   public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    EdgeEncoder3D() = default;

    /**
     * 构造函数需要知道世界系下速度
     * @param v0
     * @param speed
     */
    EdgeEncoder3D(VertexVelocity* v0, const Vec3d& speed) {
        setVertex(0, v0);
        setMeasurement(speed);
    }

    void computeError() override {
        VertexVelocity* v0 = (VertexVelocity*)_vertices[0];
        _error = v0->estimate() - _measurement;
    }

    void linearizeOplus() override { _jacobianOplusXi.setIdentity(); }

    virtual bool read(std::istream& in) { return true; }
    virtual bool write(std::ostream& out) const { return true; }
};

3 实现基于预积分和图优化的 GINS

最后我们利用前面定义的图优化顶点和边，来实现一个类似于 ESKF 的 GNSS 惯导融合定位。读者也可借这个实验来更深入地考察图优化与滤波器之间的异同。这个基于图优化的 GINS 系统逻辑和 ESKF 大体相同，一样需要静态的 IMU 初始化来确定初始的 IMU 零偏与重力方向。我们把这些逻辑处理放到一个单独的类中，重点关注这个图优化模型是如何构建的。它的基本逻辑如下：

1. 使用 IMU 静止初始化算法来获取初始的零偏（）和重力方向（），随后初始化各类信息矩阵（、、GNSS、ODOM、先验因子的信息矩阵），然后使用首个带姿态的 GNSS 数据来获取初始位置与姿态，初始速度为 0，初始的零偏等于预积分类中的零偏，即 IMU 静止初始化得到的零偏。如果 IMU 和 GNSS 都有效，就开始进行预测和优化过程。
2. 当 IMU 数据到达时，使用预积分器来累计 IMU 的积分信息。
3. 当 ODOM 数据到达时，我们将它记录为最近时刻的速度观测并保留它的读数。
4. 在 GNSS 数据到达时，先使用 last_imu_ 数据预积分到 GNSS 时刻。
5. 使用 IMU 预积分的预测值来作为优化的初始值（时刻优化的初始值，代码中为 this_frame_），构建前一个时刻的 GNSS 与当前时刻的 GNSS 间的图优化问题。当然也可以用 GNSS 的观测值来计算，两种方式的优化初值会不太一样，但在本例中结果相似。该问题的节点和边定义如下：

• 节点：前一时刻与当前时刻的位姿、速度、两个零偏，共 8 个顶点。

• 边：两个时刻间的预积分观测边，两个时刻的 GNSS 的观测边，前一个时刻的先验边，两个零偏随机游走边，速度观测边。这样一共有 7 个边。

3.1 代码实现

1. 使用 IMU 静止初始化算法来获取初始的零偏（）和重力方向（），随后初始化各类信息矩阵（、、GNSS、ODOM、先验因子的信息矩阵），然后使用首个带姿态的 GNSS 数据来获取初始位置与姿态，初始速度为 0，初始的零偏等于预积分类中的零偏，即 IMU 静止初始化得到的零偏。如果 IMU 和 GNSS 都有效，就开始进行预测和优化过程。

IMU 静止初始化代码如下：

run_gins_pre_integ.cc 主函数

          /// IMU 处理函数
          // IMU 静止初始化
          if (!imu_init.InitSuccess()) {
              imu_init.AddIMU(imu);
              return;
          }

IMU 静止初始化完成后，使用静止初始化得到的 b_g,b_a,g 初始化预积分类的，然后初始化各类信息矩阵（ b_g 、 b_a 、GNSS、ODOM、先验因子）：

run_gins_pre_integ.cc 主函数
         
          /// 需要IMU初始化
          if (!imu_inited) {
              // 读取初始零偏，设置GINS
              sad::GinsPreInteg::Options options;
              options.preinteg_options_.init_bg_ = imu_init.GetInitBg();
              options.preinteg_options_.init_ba_ = imu_init.GetInitBa();
              options.gravity_ = imu_init.GetGravity();
              gins.SetOptions(options);
              imu_inited = true;
              std::cout << "imu_inited = true" <<std::endl;
              std::cout << "imu time:" << std::fixed << std::setprecision(8) << imu.timestamp_ << std::endl;
              return;
          }

初始化各类信息矩阵的代码如下（ b_g 、 b_a 、GNSS、ODOM、先验因子），其中预积分边的信息矩阵由预积分类中的协方差矩阵之逆初始化：

void GinsPreInteg::SetOptions(sad::GinsPreInteg::Options options) {
    options_ = options;

    // 设置 bg 的信息矩阵
    double bg_rw2 = 1.0 / (options_.bias_gyro_var_ * options_.bias_gyro_var_);
    options_.bg_rw_info_.diagonal() << bg_rw2, bg_rw2, bg_rw2;

    // 设置 ba 的信息矩阵
    double ba_rw2 = 1.0 / (options_.bias_acce_var_ * options_.bias_acce_var_);
    options_.ba_rw_info_.diagonal() << ba_rw2, ba_rw2, ba_rw2;

    // 设置 GNSS 的信息矩阵
    double gp2 = options_.gnss_pos_noise_ * options_.gnss_pos_noise_;
    double gh2 = options_.gnss_height_noise_ * options_.gnss_height_noise_;
    double ga2 = options_.gnss_ang_noise_ * options_.gnss_ang_noise_;

    options_.gnss_info_.diagonal() << 1.0 / ga2, 1.0 / ga2, 1.0 / ga2, 1.0 / gp2, 1.0 / gp2, 1.0 / gh2;

    // 初始化 IMU预积分类 的 实例对象
    pre_integ_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);

    // 设置 ODOM 的信息矩阵
    double o2 = 1.0 / (options_.odom_var_ * options_.odom_var_);
    options_.odom_info_.diagonal() << o2, o2, o2;

    // 先验因子的信息矩阵
    prior_info_.block<6, 6>(9, 9) = Mat6d ::Identity() * 1e6;

    if (this_frame_) {
        this_frame_->bg_ = options_.preinteg_options_.init_bg_;
        this_frame_->ba_ = options_.preinteg_options_.init_ba_;
    }
}

当首个带姿态的 GNSS 数据到来时，使用该数据初始化初始位姿，初始速度为 0，初始的零偏等于预积分类中的零偏，即 IMU 静止初始化得到的零偏：

void GinsPreInteg::AddGnss(const GNSS& gnss) {
    this_frame_ = std::make_shared<NavStated>(current_time_);
    this_gnss_ = gnss;

    if (!first_gnss_received_) {
        if (!gnss.heading_valid_) {
            // 要求首个GNSS必须有航向
            return;
        }

        std::cout << "first gnss time:" << std::fixed << std::setprecision(8) << gnss.unix_time_ << std::endl;
        // 首个gnss信号，将初始pose设置为该gnss信号
        this_frame_->timestamp_ = gnss.unix_time_;
        this_frame_->p_ = gnss.utm_pose_.translation();
        this_frame_->R_ = gnss.utm_pose_.so3();
        this_frame_->v_.setZero();
        this_frame_->bg_ = options_.preinteg_options_.init_bg_;
        this_frame_->ba_ = options_.preinteg_options_.init_ba_;

        pre_integ_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);

        last_frame_ = this_frame_;
        last_gnss_ = this_gnss_;
        first_gnss_received_ = true;
        current_time_ = gnss.unix_time_;
        return;
    }

    //* 省略 *// 
}

2. 当 IMU 数据到达时，使用预积分器来累计 IMU 的积分信息。

void GinsPreInteg::AddImu(const IMU& imu) {
    if (first_gnss_received_ && first_imu_received_) {
        std::cout << "---IMU 预积分" << std::endl;
        pre_integ_->Integrate(imu, imu.timestamp_ - last_imu_.timestamp_);
    }

    first_imu_received_ = true;
    last_imu_ = imu;
    current_time_ = imu.timestamp_;
}

3. 当 ODOM 数据到达时，我们将它记录为最近时刻的速度观测并保留它的读数。

void GinsPreInteg::AddOdom(const sad::Odom& odom) {
    last_odom_ = odom;
    last_odom_set_ = true;
}

4. 在 GNSS 数据到达时，先使用 last_imu_ 数据预积分到 GNSS 时刻。这里 last_imu_ 比较特殊，该数据使用了两次，这是第二次使用（第一次是前面的预积分），使用该数据预积分到当前 GNSS 的时刻：

void GinsPreInteg::AddGnss(const GNSS& gnss) {
    this_frame_ = std::make_shared<NavStated>(current_time_);
    this_gnss_ = gnss;

    //* 省略 *//

    // 积分到GNSS时刻
    // 这部分为什么可以积分到GNSS时刻 ???
    // 这个特殊的 last_imu_ 数据使用了两次，这是第二次使用（第一次是前面的预积分）。预积分到当前GNSS的时刻
    pre_integ_->Integrate(last_imu_, gnss.unix_time_ - current_time_);

    current_time_ = gnss.unix_time_;
    // last_frame_ 和 this_frame_，使用 IMU 预积分的预测值来作为优化的初始值（this_frame_）
    *this_frame_ = pre_integ_->Predict(*last_frame_, options_.gravity_);

    Optimize();

    last_frame_ = this_frame_;
    last_gnss_ = this_gnss_;
}

5. 使用 IMU 预积分的预测值来作为优化的初始值（时刻优化的初始值，代码中为 this_frame_），构建前一个时刻的 GNSS 与当前时刻的 GNSS 间的图优化问题。

注意：①优化完成后将优化后的值重新赋值给 last_frame_ 和 this_frame_，并且使用优化后的 b_g,b_a 重置预积分实例对象。②这里没有先验因子的信息矩阵进行更新处理，后续第 8 章会探究先验因子信息矩阵的设置及更新。

void GinsPreInteg::Optimize() {
    if (pre_integ_->dt_ < 1e-3) {
        // 未得到积分
        return;
    }

    // 创建可变尺寸的 BlockSolver
    using BlockSolverType = g2o::BlockSolverX;
    using LinearSolverType = g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType>;

    auto* solver = new g2o::OptimizationAlgorithmLevenberg(
        g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm(solver);

    // 上时刻顶点， pose, v, bg, ba
    auto v0_pose = new VertexPose();
    v0_pose->setId(0);
    v0_pose->setEstimate(last_frame_->GetSE3());
    optimizer.addVertex(v0_pose);

    auto v0_vel = new VertexVelocity();
    v0_vel->setId(1);
    v0_vel->setEstimate(last_frame_->v_);
    optimizer.addVertex(v0_vel);

    auto v0_bg = new VertexGyroBias();
    v0_bg->setId(2);
    v0_bg->setEstimate(last_frame_->bg_);
    optimizer.addVertex(v0_bg);

    auto v0_ba = new VertexAccBias();
    v0_ba->setId(3);
    v0_ba->setEstimate(last_frame_->ba_);
    optimizer.addVertex(v0_ba);

    // 本时刻顶点，pose, v, bg, ba
    // this_frame_ 是从 起始点last_frame_ 开始通过 IMU预积分 得到的预测值，在这里作为图优化的初始值。
    auto v1_pose = new VertexPose();
    v1_pose->setId(4);
    v1_pose->setEstimate(this_frame_->GetSE3());
    optimizer.addVertex(v1_pose);

    auto v1_vel = new VertexVelocity();
    v1_vel->setId(5);
    v1_vel->setEstimate(this_frame_->v_);
    optimizer.addVertex(v1_vel);

    auto v1_bg = new VertexGyroBias();
    v1_bg->setId(6);
    v1_bg->setEstimate(this_frame_->bg_);
    optimizer.addVertex(v1_bg);

    auto v1_ba = new VertexAccBias();
    v1_ba->setId(7);
    v1_ba->setEstimate(this_frame_->ba_);
    optimizer.addVertex(v1_ba);

    // 预积分边
    auto edge_inertial = new EdgeInertial(pre_integ_, options_.gravity_);
    edge_inertial->setVertex(0, v0_pose);
    edge_inertial->setVertex(1, v0_vel);
    edge_inertial->setVertex(2, v0_bg);
    edge_inertial->setVertex(3, v0_ba);
    edge_inertial->setVertex(4, v1_pose);
    edge_inertial->setVertex(5, v1_vel);
    auto* rk = new g2o::RobustKernelHuber();
    rk->setDelta(200.0);
    edge_inertial->setRobustKernel(rk);
    optimizer.addEdge(edge_inertial);

    // 两个零偏随机游走
    auto* edge_gyro_rw = new EdgeGyroRW();
    edge_gyro_rw->setVertex(0, v0_bg);
    edge_gyro_rw->setVertex(1, v1_bg);
    edge_gyro_rw->setInformation(options_.bg_rw_info_);
    optimizer.addEdge(edge_gyro_rw);

    auto* edge_acc_rw = new EdgeAccRW();
    edge_acc_rw->setVertex(0, v0_ba);
    edge_acc_rw->setVertex(1, v1_ba);
    edge_acc_rw->setInformation(options_.ba_rw_info_);
    optimizer.addEdge(edge_acc_rw);

    // 上时刻先验
    auto* edge_prior = new EdgePriorPoseNavState(*last_frame_, prior_info_);
    edge_prior->setVertex(0, v0_pose);
    edge_prior->setVertex(1, v0_vel);
    edge_prior->setVertex(2, v0_bg);
    edge_prior->setVertex(3, v0_ba);
    optimizer.addEdge(edge_prior);

    // GNSS边
    auto edge_gnss0 = new EdgeGNSS(v0_pose, last_gnss_.utm_pose_);
    edge_gnss0->setInformation(options_.gnss_info_);
    optimizer.addEdge(edge_gnss0);

    auto edge_gnss1 = new EdgeGNSS(v1_pose, this_gnss_.utm_pose_);
    edge_gnss1->setInformation(options_.gnss_info_);
    optimizer.addEdge(edge_gnss1);

    // Odom边
    EdgeEncoder3D* edge_odom = nullptr;
    Vec3d vel_world = Vec3d::Zero();
    Vec3d vel_odom = Vec3d::Zero();
    if (last_odom_set_) {
        // velocity obs
        double velo_l =
            options_.wheel_radius_ * last_odom_.left_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
        double velo_r =
            options_.wheel_radius_ * last_odom_.right_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
        double average_vel = 0.5 * (velo_l + velo_r);
        vel_odom = Vec3d(average_vel, 0.0, 0.0);
        vel_world = this_frame_->R_ * vel_odom;

        edge_odom = new EdgeEncoder3D(v1_vel, vel_world);
        edge_odom->setInformation(options_.odom_info_);
        optimizer.addEdge(edge_odom);

        // 重置odom数据到达标志位，等待最新的odom数据
        last_odom_set_ = false;
    }

    optimizer.setVerbose(options_.verbose_);
    optimizer.initializeOptimization();
    optimizer.optimize(20);

    if (options_.verbose_) {
        // 获取结果，统计各类误差
        LOG(INFO) << "chi2/error: ";
        LOG(INFO) << "preintegration: " << edge_inertial->chi2() << "/" << edge_inertial->error().transpose();
        // LOG(INFO) << "gnss0: " << edge_gnss0->chi2() << ", " << edge_gnss0->error().transpose();
        LOG(INFO) << "gnss1: " << edge_gnss1->chi2() << ", " << edge_gnss1->error().transpose();
        LOG(INFO) << "bias: " << edge_gyro_rw->chi2() << "/" << edge_acc_rw->error().transpose();
        LOG(INFO) << "prior: " << edge_prior->chi2() << "/" << edge_prior->error().transpose();
        if (edge_odom) {
            LOG(INFO) << "body vel: " << (v1_pose->estimate().so3().inverse() * v1_vel->estimate()).transpose();
            LOG(INFO) << "meas: " << vel_odom.transpose();
            LOG(INFO) << "odom: " << edge_odom->chi2() << "/" << edge_odom->error().transpose();
        }
    }

    last_frame_->R_ = v0_pose->estimate().so3();
    last_frame_->p_ = v0_pose->estimate().translation();
    last_frame_->v_ = v0_vel->estimate();
    last_frame_->bg_ = v0_bg->estimate();
    last_frame_->ba_ = v0_ba->estimate();

    this_frame_->R_ = v1_pose->estimate().so3();
    this_frame_->p_ = v1_pose->estimate().translation();
    this_frame_->v_ = v1_vel->estimate();
    this_frame_->bg_ = v1_bg->estimate();
    this_frame_->ba_ = v1_ba->estimate();

    // 重置integ
    // 更新 bg、ba，重置预积分
    options_.preinteg_options_.init_bg_ = this_frame_->bg_;
    options_.preinteg_options_.init_ba_ = this_frame_->ba_;
    pre_integ_ = std::make_shared<IMUPreintegration>(options_.preinteg_options_);
}

最后运行基于图优化的GINS：

    /// 设置各类回调函数
    io.SetIMUProcessFunc([&](const sad::IMU& imu) {
          if (imu_init.InitSuccess()){
            std::cout << "IMU 处理函数!    " << "imu_inited:" << imu_inited << "    gnss_inited:" << gnss_inited << std::endl;
          }
          /// IMU 处理函数
          // IMU 静止初始化
          if (!imu_init.InitSuccess()) {
              imu_init.AddIMU(imu);
              return;
          }

          /// 需要IMU初始化
          if (!imu_inited) {
              // 读取初始零偏，设置GINS
              sad::GinsPreInteg::Options options;
              options.preinteg_options_.init_bg_ = imu_init.GetInitBg();
              options.preinteg_options_.init_ba_ = imu_init.GetInitBa();
              options.gravity_ = imu_init.GetGravity();
              gins.SetOptions(options);
              imu_inited = true;
              std::cout << "imu_inited = true" <<std::endl;
              std::cout << "imu time:" << std::fixed << std::setprecision(8) << imu.timestamp_ << std::endl;
              return;
          }

          if (!gnss_inited) {
              /// 等待有效的RTK数据
              return;
          }

          // 与 ESKF 不同之处！！！  
          /// GNSS 也接收到之后，再开始进行预测
          gins.AddImu(imu);

          auto state = gins.GetState();
          save_result(fout, state);
          if (ui) {
              ui->UpdateNavState(state);
              usleep(5e2);
          }
      })
        .SetGNSSProcessFunc([&](const sad::GNSS& gnss) {
            if (imu_init.InitSuccess()){
              std::cout << "GNSS 处理函数!    " << "imu_inited:" << imu_inited << "    gnss_inited:" << gnss_inited << std::endl;
            }
            /// GNSS 处理函数
            if (!imu_inited) {
                return;
            }

            // heading_valid_ 数据由 GNSS 构造函数确定
            sad::GNSS gnss_convert = gnss;
            if (!sad::ConvertGps2UTM(gnss_convert, antenna_pos, FLAGS_antenna_angle) || !gnss_convert.heading_valid_) {
                return;
            }

            /// 去掉原点
            if (!first_gnss_set) {
                origin = gnss_convert.utm_pose_.translation();
                first_gnss_set = true;
                std::cout << "gnss_inited = true" <<std::endl;
                std::cout << "gnss time:" << std::fixed << std::setprecision(8) << gnss_convert.unix_time_ << std::endl;
            }
            gnss_convert.utm_pose_.translation() -= origin;

            // 与 ESKF 不同之处！！！
            gins.AddGnss(gnss_convert);

            auto state = gins.GetState();
            save_result(fout, state);
            if (ui) {
                ui->UpdateNavState(state);
                usleep(1e3);
            }
            gnss_inited = true;
        })
        .SetOdomProcessFunc([&](const sad::Odom& odom) {
            if (imu_init.InitSuccess()){
              std::cout << "ODOM 处理函数!    " << "imu_inited:" << imu_inited << "    gnss_inited:" << gnss_inited << std::endl;
            }
            imu_init.AddOdom(odom);

            if (imu_inited && gnss_inited) {
                // 与 ESKF 不同之处！！！
                gins.AddOdom(odom);
            }
        })
        .Go();

3.2 运行结果

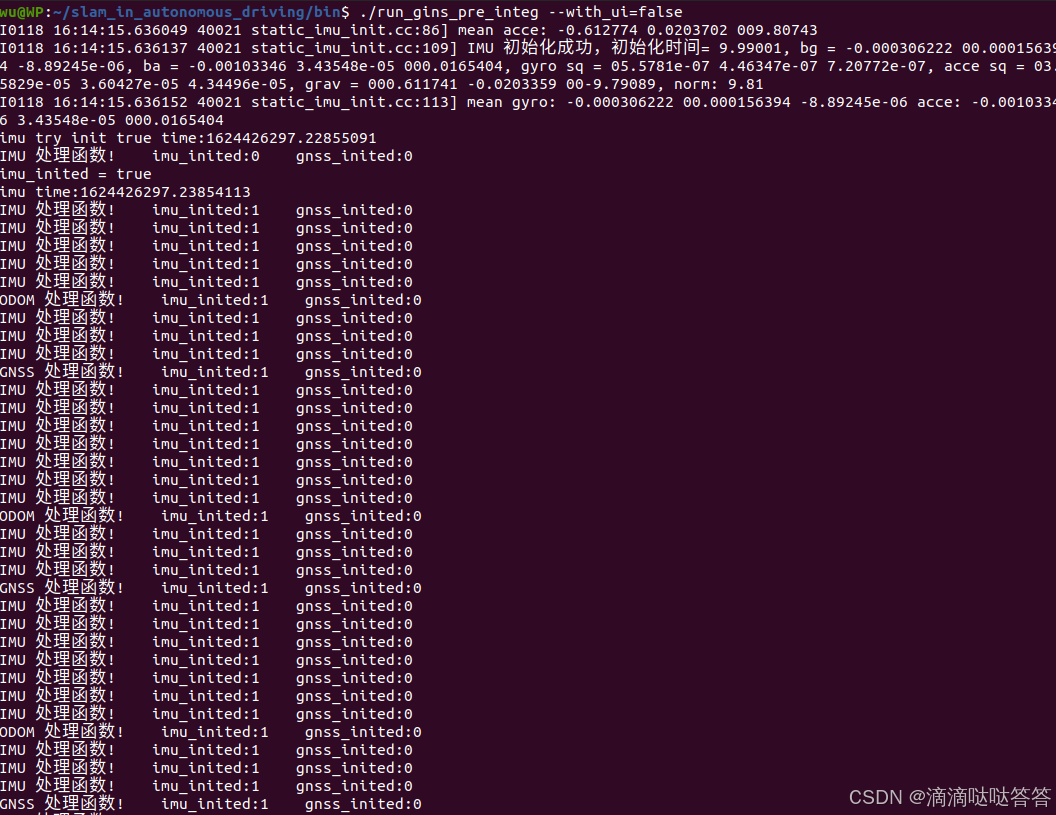
IMU 静止初始化结果：

I0118 16:14:15.636049 40021 static_imu_init.cc:86] mean acce: -0.612774 0.0203702 009.80743
I0118 16:14:15.636137 40021 static_imu_init.cc:109] IMU 初始化成功，初始化时间= 9.99001, bg = -0.000306222 00.000156394 -8.89245e-06, ba = -0.00103346 3.43548e-05 000.0165404, gyro sq = 05.5781e-07 4.46347e-07 7.20772e-07, acce sq = 03.5829e-05 3.60427e-05 4.34496e-05, grav = 000.611741 -0.0203359 00-9.79089, norm: 9.81
I0118 16:14:15.636152 40021 static_imu_init.cc:113] mean gyro: -0.000306222 00.000156394 -8.89245e-06 acce: -0.00103346 3.43548e-05 000.0165404

某一轮优化过程：

GNSS 处理函数!    imu_inited:1    gnss_inited:1
iteration= 0	 chi2= 11.939758	 time= 2.537e-05	 cumTime= 2.537e-05	 edges= 7	 schur= 0	 lambda= 6666674.355996	 levenbergIter= 1
iteration= 1	 chi2= 11.937747	 time= 1.0831e-05	 cumTime= 3.6201e-05	 edges= 7	 schur= 0	 lambda= 4444449.570664	 levenbergIter= 1
iteration= 2	 chi2= 11.934778	 time= 1.069e-05	 cumTime= 4.6891e-05	 edges= 7	 schur= 0	 lambda= 2962966.380443	 levenbergIter= 1
iteration= 3	 chi2= 11.930420	 time= 1.0512e-05	 cumTime= 5.7403e-05	 edges= 7	 schur= 0	 lambda= 1975310.920295	 levenbergIter= 1
iteration= 4	 chi2= 11.924066	 time= 1.0654e-05	 cumTime= 6.8057e-05	 edges= 7	 schur= 0	 lambda= 1213094.557098	 levenbergIter= 1
iteration= 5	 chi2= 11.914094	 time= 1.074e-05	 cumTime= 7.8797e-05	 edges= 7	 schur= 0	 lambda= 549789.382063	 levenbergIter= 1
iteration= 6	 chi2= 11.893194	 time= 1.048e-05	 cumTime= 8.9277e-05	 edges= 7	 schur= 0	 lambda= 183263.127354	 levenbergIter= 1
iteration= 7	 chi2= 11.834372	 time= 1.0341e-05	 cumTime= 9.9618e-05	 edges= 7	 schur= 0	 lambda= 61087.709118	 levenbergIter= 1
iteration= 8	 chi2= 11.669598	 time= 1.0288e-05	 cumTime= 0.000109906	 edges= 7	 schur= 0	 lambda= 20362.569706	 levenbergIter= 1
iteration= 9	 chi2= 11.239074	 time= 1.0601e-05	 cumTime= 0.000120507	 edges= 7	 schur= 0	 lambda= 6787.523235	 levenbergIter= 1
iteration= 10	 chi2= 10.292144	 time= 1.0354e-05	 cumTime= 0.000130861	 edges= 7	 schur= 0	 lambda= 2262.507745	 levenbergIter= 1
iteration= 11	 chi2= 8.562370	 time= 1.046e-05	 cumTime= 0.000141321	 edges= 7	 schur= 0	 lambda= 754.169248	 levenbergIter= 1
iteration= 12	 chi2= 5.795209	 time= 1.0682e-05	 cumTime= 0.000152003	 edges= 7	 schur= 0	 lambda= 251.389749	 levenbergIter= 1
iteration= 13	 chi2= 3.136536	 time= 1.0396e-05	 cumTime= 0.000162399	 edges= 7	 schur= 0	 lambda= 83.796583	 levenbergIter= 1
iteration= 14	 chi2= 2.276110	 time= 1.071e-05	 cumTime= 0.000173109	 edges= 7	 schur= 0	 lambda= 27.932194	 levenbergIter= 1
iteration= 15	 chi2= 2.216088	 time= 1.0856e-05	 cumTime= 0.000183965	 edges= 7	 schur= 0	 lambda= 9.310731	 levenbergIter= 1
iteration= 16	 chi2= 2.215426	 time= 1.0525e-05	 cumTime= 0.00019449	 edges= 7	 schur= 0	 lambda= 6.207154	 levenbergIter= 1
iteration= 17	 chi2= 2.215425	 time= 1.051e-05	 cumTime= 0.000205	 edges= 7	 schur= 0	 lambda= 4.138103	 levenbergIter= 1
iteration= 18	 chi2= 2.215425	 time= 1.0608e-05	 cumTime= 0.000215608	 edges= 7	 schur= 0	 lambda= 2.758735	 levenbergIter= 1
iteration= 19	 chi2= 2.215425	 time= 1.0528e-05	 cumTime= 0.000226136	 edges= 7	 schur= 0	 lambda= 1.839157	 levenbergIter= 1
I0118 16:15:22.336377 40077 gins_pre_integ.cc:240] chi2/error: 
I0118 16:15:22.336380 40077 gins_pre_integ.cc:241] preintegration: 0.00249247/05.70395e-08 -2.69427e-08 -6.17484e-07 -0.000170989 -9.10803e-05 09.26133e-07 -1.31586e-05 -6.98776e-06 07.65849e-08
I0118 16:15:22.336386 40077 gins_pre_integ.cc:243] gnss1: 0.0543654, 00.00120472 -0.00234341 00.00125066 000.0156347 -0.00404241 -0.00189687
I0118 16:15:22.336392 40077 gins_pre_integ.cc:244] bias: 0/0 0 0
I0118 16:15:22.336395 40077 gins_pre_integ.cc:245] prior: 1.69277/000.00167301 0-0.00260842 00-0.0103468 -7.47095e-05 00.000265061 00.000486168 000-0.128167 00-0.0195928 00.000358022 -1.37342e-07 0001.857e-07 06.22816e-07 01.71906e-06 09.29327e-07 00-9.148e-09
I0118 16:15:22.336407 40077 gins_pre_integ.cc:247] body vel: 0000.612737 000.0214819 -0.00161771
I0118 16:15:22.336410 40077 gins_pre_integ.cc:248] meas: 0.584907 00000000 00000000
I0118 16:15:22.336413 40077 gins_pre_integ.cc:249] odom: 0.405799/00000.031448 000.00505169 -1.74854e-05

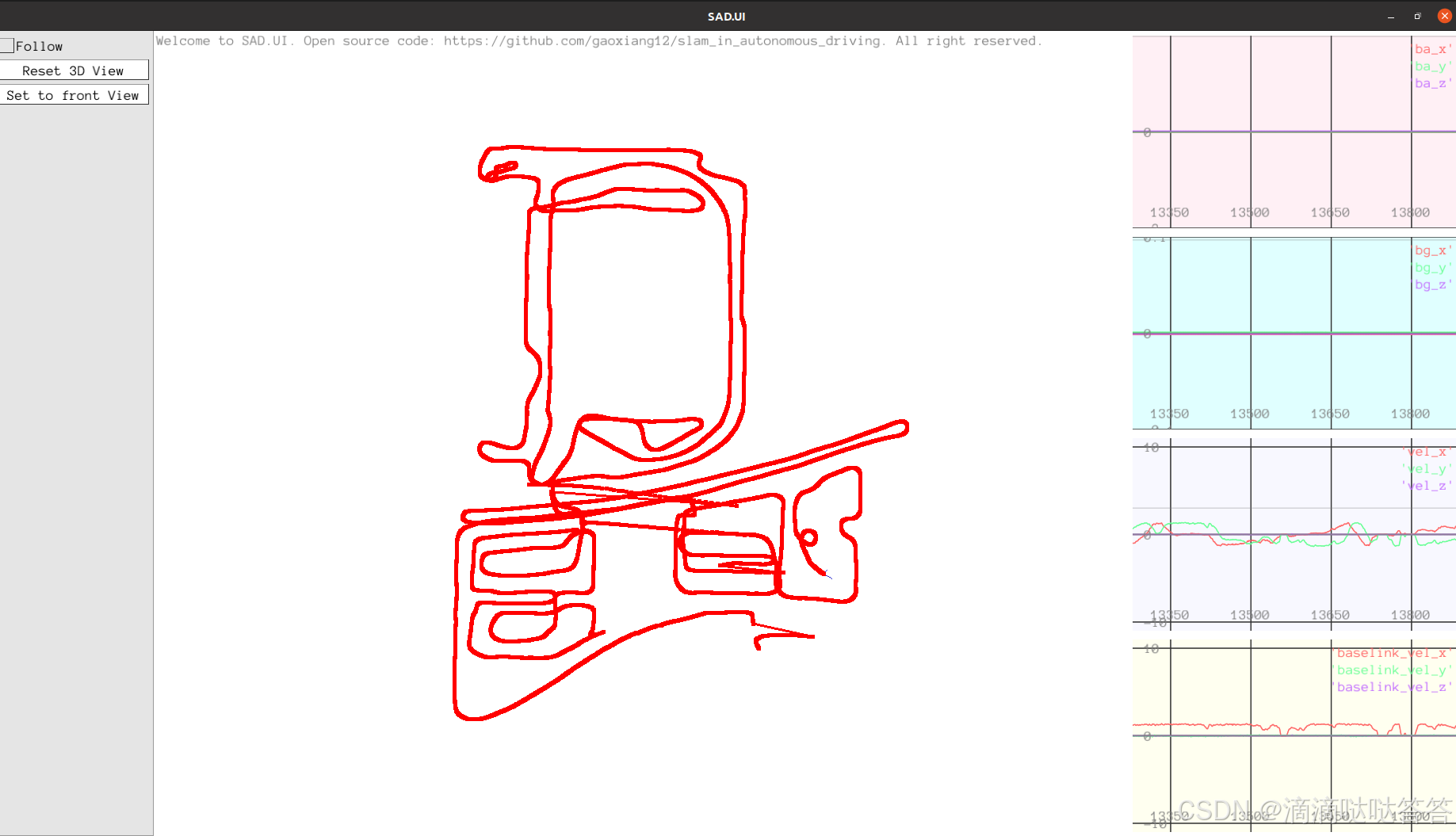
实时运行结果：

3.3 总结

3.3.1 图优化和 ESKF 的区别

1. 相比 ESKF，基于预积分的图优化方案可以累积 IMU 读数。累积多少时间，或者每次迭代优化取多少次，都可以人为选择。而 ESKF 默认只能迭代一次，预测也只依据单个时刻的IMU 数据。
2. 预积分边（或者用因子图优化的方法，称 IMU 因子或预积分因子）是一个很灵活的因子。它关联的六个顶点都可以发生变化。为了保持状态不发生随意改变，预积分因子通常要配合其他因子一起使用。在我们的案例中，两端的 GNSS 因子可以限制位姿的变化，ODOM 因子可以限制速度的改变，两个零偏因子会限制零偏的变化量，但不限制零偏的绝对值。
3. 先验因子会让整个估计变得更平滑。严格来说，先验因子的协方差矩阵还需要使用边缘化来操作。因为本章主要介绍预积分原理，所以我们给先验因子设定了固定大小的信息矩阵，来简化程序中的一些实现。本书的第 8 章中，我们会谈论先验因子信息矩阵的设定和代码实现方式。读者可以尝试去除本因子，看看轨迹估计会产生什么影响。
4. 图优化让我们很方便地设置核函数，回顾各个因子占据的误差大小，进而确定优化过程主要受哪一部分影响。例如，我们可以分析正常情况下 RTK 观测应该产生多少残差，而异常情况下应该产生多少残差，从而确定 GNSS 是否给出了正确的位姿读数。后面我们还会向读者介绍如何来控制优化流程以实现更鲁棒的效果。读者可以打开本程序的调试输出，查看这些信息。
5. 由于引入了更多计算，图优化的耗时明显要高于滤波器方案。不过，智能汽车的算力相比以往有了明显的增加，目前图优化在一些实时计算里也可以很好地使用了。

3.3.2 总结

本章介绍了预积分的基本原理，包括它的观测模型、噪声模型、雅可比推导方式以及针对零偏的处理方式。读者在实践当中也可以灵活应用预积分：

若不考虑优化，那么预积分和直接积分完全等同；预积分可以用于预测后续状态。
用于优化时，预积分可以方便地建模两帧间的相对运动。如果固定 IMU 零偏，还可以大幅简化预积分模型。如果考虑零偏，那么需要针对零偏的更新，来更新预积分的观测；
预积分模型可以很容易地与其他图优化模型进行融合，在同一个问题中进行优化。也可以很方便地设置积分时间、优化帧数等参数，相比于滤波器方案更加自由。