图
图的顶点集不能为空
稀疏图:一般满足 |E| < |V| log|V|,可以讲G视为稀疏图
图的存储及基本操作
邻接矩阵法(更适用于稠密图)
邻接矩阵法:用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(即各顶点之间的邻接关系);存储定点之间邻接关系的二维数组称为邻接矩阵。
- 一般在简单应用中,可直接用二维数组作为图的邻接矩阵(顶点信+息可以忽略)
- 无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储
邻接表法(更适用于稀疏图)
当图为稀疏图时,使用邻接矩阵法会浪费大量的存储空间,而图的邻接表法结合了顺序存储和链式存储方法,大大减少了这种不必要的浪费。
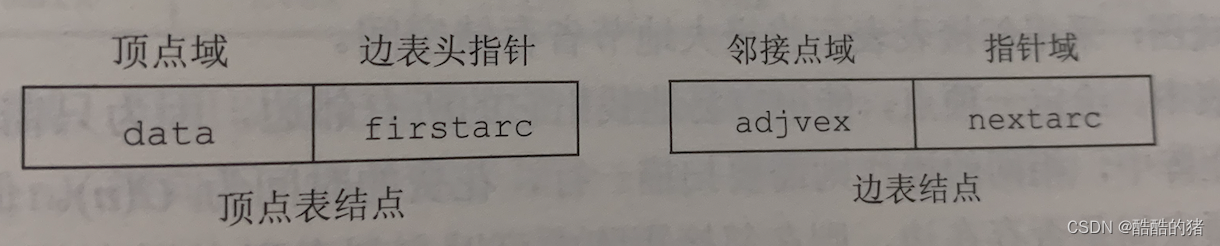
邻接表法:对图G中的每个顶点Vi建立一个单链表,第i个单链表中的节点表示依附于顶点Vi的边(对于有向图则是以顶点Vi结尾的狐),这个单链表就称为顶点Vi的边表(对于有向图称为出边表)。边表的头指针和顶点的数据信息采用顺序存储(称为顶点表),所以在邻接表中存在两种结点:顶点表结点和边表结点。
十字链表
十字链表是有向图的一种链式存储结构。在十字链表中,对应于有向图中的每条弧有一个结点,对应于每个顶点也有一个结点。
在弧结点中有五个域:尾域和头域分别指示弧尾和弧头这两个顶点在图中的位置;链域hlink指向弧头相同的下一条弧;链域tlink指向弧尾相同的下一条弧;info指向该弧的相关信息。(弧头相同的弧就在同一条链表上,弧尾相同的弧也在同一个链表上)
顶点结点有三个域:data域存放顶点相关的数据信息,如顶点名称;firstin和firstout两个域分别指向以该顶点为弧头或弧尾的第一个弧结点。
在十字链表中,容易找到Vi为尾的弧,也容易找到Vi为头的弧,因而容易求得顶点的出度和入度。图的十字链表表示是不唯一的,但一个十字链表表示确定一个图。
邻接多重表
邻接多重表是无向图的另一种链式存储结构。
在邻接多重表中,每条边用一个结点表示:(mark, ivex, ilink, jvex, blink, info)
- mark用来标记,可用以该条边是否被搜索过;
- ivex和jvex:为该边依附的两个顶点在图中的位置
- ilink:指向下一条依附于顶点ivex的边
- jlink:指向下一条依附于顶点jvex的边
- info:指向和边相关的各种信息
每个顶点也用一个结点表示:(data, firstedge) - data:存储该顶点的相关信息
- firstedge:指示第一条依附于该顶点的边
图的基本操作
图的基本操作是独立图的基本结构的。
//图的基本操作主要包括:
Adjacent(G, x, y) //判断图G是否存在边<x,y>或(x,y)
Neighbors(G, x) //列出图G中与结点x邻接的边
InsertVertex(G, x) //在图G中插入顶点x
DeleteVertex(G, x) //在图G中删除顶点x
AddEdge(G, x, y) //若无向边(x,y)或有向边<x,y>不存在,则向图G中添加该边
RemoveEdge(G, x, y) //若无向边(x,y)或有向边<x,y>不存在,则向图G中删除该边
FirstNeighbor(G, x) //求图G中顶点x的第一个邻接点,若有则返回顶点号。若x没有邻接点或图中不存在x,则返回-1
NextNeighbor(G, x, y) //假设图G中顶点y是顶点x的一个邻接点,返回除y外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,返回-1
Get_edge_value(G, x, y)