我们之前学习了 pytorch 中的基本数据 tensor
今天我们要开始学习 pytorch 的简单工作流程了
数据 -> 构建或选择一个预训练的模型 -> 使得模型适应数据并能够进行预测 -> 评估模型 -> 通过实验提升性能 -> 保存并重新加载你训练的模型
机器学习和深度学习的关键是从过去获得的数据中,创建算法来发现数据中的模式,接着用我们所发现的模式来预测将来。
接下来我们就尝试使用pytorch创建一个模型,主要是一个线性模型。
what_were_covering = { 1:"data(preparing and loading)",
2:"build model",
3:"fitting the model to data(training)",
4:"making predictions and evaluating a model (inference)",
5:"saving and loading a model",
6:"putting it all together"
}
1 data(preparing and loading)
首先,我们导入必须要的包,同时查看一下pytorch的版本
import torch
import matplotlib.pyplot as plt
import torch.nn as nn
torch.__version__
‘2.3.1+cu118’
机器学习就像一个包含两个方面的游戏:
1 将你的数据(图像、音频、视频、文本等)进行数学的表征
2 创建或者选择模型尽可能好地来学习这些表征
weights = 0.7
bias = 0.3
start = 0
end = 1
step = 0.02
# 之前我们学习过, unsqueeze(dim=1)就是在列上增加单维度,这样我们的每个数据外面就有一个方括号了
# 这里 dim = 1, 大家可以自己试一试,可以把 unsqueeze(dim=1) 删除看看是什么形状
X = torch.arange(start, end, step).unsqueeze(dim = 1)
y = weights * X + bias
print(X[:10], y[:10])
print(len(X))
print(len(y))
tensor([[0.0000],
[0.0200],
[0.0400],
[0.0600],
[0.0800],
[0.1000],
[0.1200],
[0.1400],
[0.1600],
[0.1800]]) tensor([[0.3000],
[0.3140],
[0.3280],
[0.3420],
[0.3560],
[0.3700],
[0.3840],
[0.3980],
[0.4120],
[0.4260]])
50
50
将我们的数据划分为训练集和测试集
一般训练集占数据的 60%~80%,测试集占 20%~40%
注意:当我们处理真实世界的数据集时,在项目的开始我们就需要划分数据,(测试数据集应该要一直和其他数据集分开),以使得我们的模型在测试集上进行测试,促进模型在它没有遇到过的数据上有更好的泛化性能
# 划分训练集和测试集
train_split = int (0.8 * len(X))
X_train, y_train = X[:train_split], y[:train_split]
X_test, y_test = X[train_split:], y[train_split:]
len(X_train), len(y_train), len(X_test), len(y_test)
(40, 40, 10, 10)
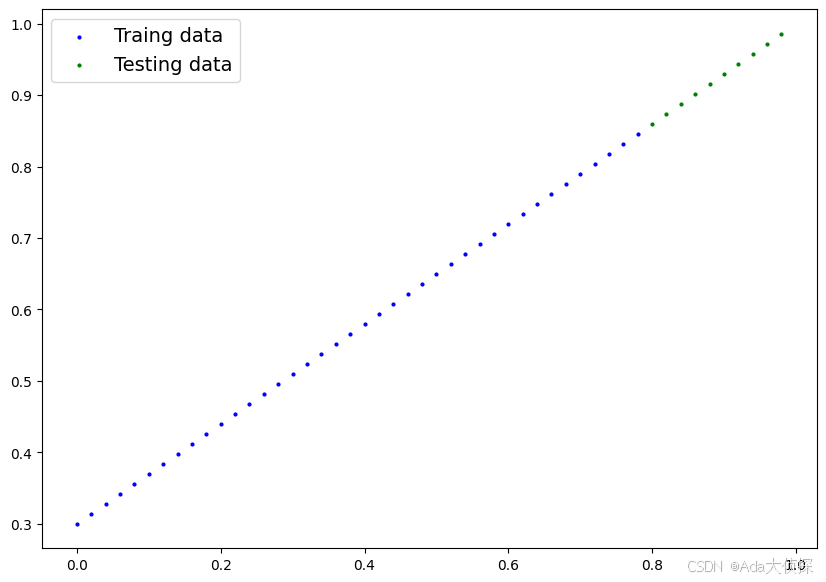
我们刚开始学习东西搞不明白,最好是将我们学习的内容进行可视化,那让我们来具体看一看这些数据究竟是什么形态的吧!
唔,我还发现优秀的开发者,都比较喜欢把这些功能啥的函数话,那我们也来搞一个函数,功能就是绘画出我们的训练数据、真实值、预测值的函数
# 我刚开始学东西搞不懂,也喜欢把东西可视化,让我们具体来看看这些数据是什么形态的
# 我还发现优秀的代码编写者都喜欢把一件事情搞成一个函数来进行
def plot_predictions(train_data=X_train,
train_labels=y_train,
test_data=X_test,
test_labels=y_test,
predictions=None):
'''
plots training data, test data and compares predictions.
'''
plt.figure(figsize=(10, 7))
# 用蓝色来描绘训练数据, s是size的意思,可以试试其他的值还挺有意思的
plt.scatter(train_data, train_labels, c="b", s=4, label="Traing data")
# 用绿色来描绘测试数据
plt.scatter(test_data, test_labels, c="g", s=4, label="Testing data")
if predictions is not None:
# 用红色来描绘预测数据
plt.scatter(test_data, predictions, c="r", s=4, label="prediction data")
# 展示标签
plt.legend(prop={"size":14})
plot_predictions()
2 build model (创建模型)
import torch.nn as nn
import torch
class LinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.weights = nn.Parameter(torch.randn(1,
dtype=torch.float),
requires_grad=True)
self.bias = nn.Parameter(torch.randn(1,
dtype=torch.float),
requires_grad=True)
def forward(self, x):
return self.weights * x + self.bias
pytorch有四个比较基础且重要的模块,基本都要用到:
torch.nn
torch.optim
torch.utils.data.Dataset
torch.utils.data.DataLoader
(1) torch.nn 包含了计算图的所有构建块(本质上是一系列以特定方式执行的计算)
(2) torch.nn.Module 神经网络模块的基本类,如果使用pytorch创建神经网路,你的模型必须是nn.Module的子类,同时需要实现forward(),我现在懂了,forward()表示前向传播,用数学实现往前传就可以
(3) torch.optim 优化,对梯度的改变进行优化,让它以一种更好的方式进行训练同时减少损失或者说是代价
接着,我们来看看如何查找pytorch模型中的参数内容
首先,我们需要创建一个模型,通过上述创建我们模型的方法,不难发现,我们参数是用 torch.randn()来创建的,是个随机数,因此我们在这里使用torch.manual_seed()使得结果能够复现
# 由于nn.Parameter是随机的,因此我们使用 manual_seed() 来复现实验
torch.manual_seed(42)
# 创建一个模型实例
model_0 = LinearRegressionModel()
# 查看模型的参数
# 这行代码报错,所以我们有了list
# model_0.parameters()
# <generator object Module.parameters at 0x0000020AF1316C80>
list(model_0.parameters())
[Parameter containing:
tensor([0.3367], requires_grad=True),
Parameter containing:
tensor([0.1288], requires_grad=True)]
我们也可以使用 .state_dict() 来获得模型的状态(这个模型包含什么内容、参数啥的)
# 列出 参数的名称和它的内容
model_0.state_dict()
OrderedDict([(‘weights’, tensor([0.3367])), (‘bias’, tensor([0.1288]))])
我感觉这个 .state_dict() 比 .parameters() 好一些,数据内涵和内容更加清晰
实际上,我们希望从随机参数开始,让模型更新她们,来适应我们数据的最佳参数,就是我们自己定义的 weights 和 bias 值。
使用 torch.inference_mode()进行预测
# 用模型进行预测
with torch.inference_mode():
y_preds = model_0(X_test)
with torch.no_grad():
y_preds = model_0(X_test)
这是个啥,就是说我们进行训练的时候需要使用梯度来更新我们的参数值,而预测的时候我们是不需要梯度的,少了这个梯度计算的过程能够减少计算,尤其是有大量数据的时候。
上文中的 torch.inference_mode() 和 torch.no_grad() 都是同样的作用,不过前者是后来更新的,能够更快更方便使用。
# 让我们来进行预测吧
print(f"测试样本的数量:{len(X_test)}")
print(f"预测:{len(y_preds)}")
print(f"预测值:{y_preds}")
测试样本的数量:10
预测:10
预测值:tensor([[0.3982],
[0.4049],
[0.4116],
[0.4184],
[0.4251],
[0.4318],
[0.4386],
[0.4453],
[0.4520],
[0.4588]])
接下来让我们可视化的看一看吧,使用我们自己创建的函数捏
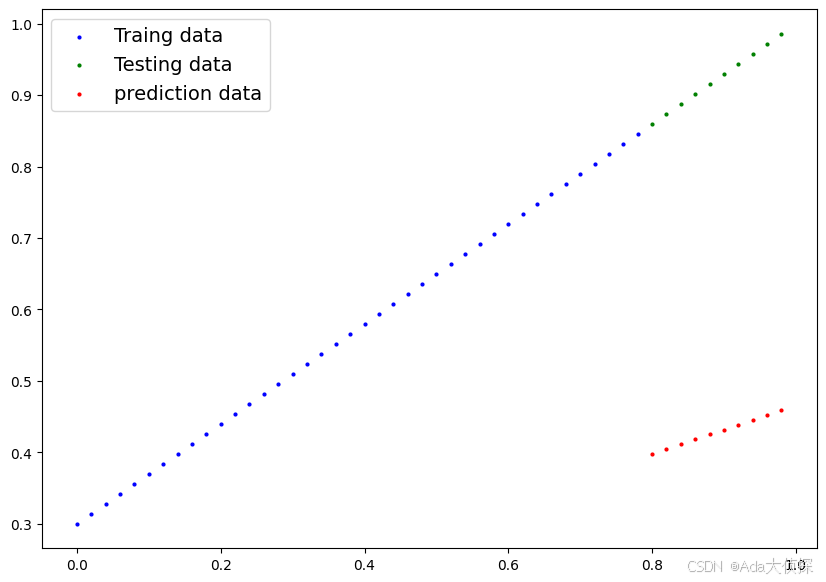
plot_predictions(predictions=y_preds)
很明显,我们希望预测值和真实值之间差距越小越好,越接近0越好,显然,咱们这个预测是相当不好的
为什么呢?很简单,我们的 weights 和 bias 都是随机的值,它并没有根据我们的训练集生成,所以理所当然的预测值很糟糕
3 训练模型 和 预测评估
大多数情况下,我们是不知道数据理想的参数的,事实上,我们需要写代码看看是否模型能够找到理性的参数值
创建损失函数和使用pytorch的优化器
如果需要更新我们的参数,那么我们就需要损失函数和优化器
loss function:损失函数,一个衡量我们模型的代价的函数,看看我们的模型到底有多差的一个函数。根据预测值和真实值之间的比较,越低越好哈。eg:torch.nn.L1Loss()Mean absolute error平均绝对误差;torch.nn.BCELoss() Binary cross entropy for binary classification进行二分类的
optimizer:优化器,告诉我们的模型如何去更新梯度,同时能更好的降低损失。 eg:Stochastic(随机) gradient desent,torch.optim.SGD(); Adam optimizer,torch.optim.Adam()
同时我们还需要 train 循环和 test 循环来帮助我们实现这个事情
import torch.optim as optim
loss_fn = nn.L1Loss()
optimizer = optim.SGD(model_0.parameters(), lr=0.01)
# 开始正式写我们的训练部分了
epochs = 100
# 让我们定义一些容器来存储一些比较重要的内容,同时也可以方便我们画图和理解这些内涵
epoch_count = []
loss_train = []
loss_test_value = []
for epoch in range(epochs):
# 模型进入训练模式
model_0.train()
y_pred = model_0(X_train)
loss = loss_fn(y_pred, y_train)
# print(f"loss:{loss}")
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print(f"parameters:{model_0.state_dict()}")
# 模型进入评估模式
model_0.eval()
with torch.inference_mode():
y_test_preds = model_0(X_test)
loss_test = loss_fn(y_test_preds, y_test)
if epoch % 10 == 0:
epoch_count.append(epoch)
loss_test_value.append(loss_test.detach().numpy())
loss_train.append(loss.detach().numpy())
print(f"Epoch:{epoch} | loss_test_value:{loss_test_value} | loss_train:{loss_train}")
一条结果我摘出来了,是这样的,方便大家观看和理解。
Epoch:0 | loss_test_value:[array(0.48106518, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32)]
Epoch:0 | loss_test_value:[array(0.48106518, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32)]
Epoch:10 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32)]
Epoch:20 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32)]
Epoch:30 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32)]
Epoch:40 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32)]
Epoch:50 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32), array(0.09919948, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32), array(0.04167863, dtype=float32)]
Epoch:60 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32), array(0.09919948, dtype=float32), array(0.08886633, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32), array(0.04167863, dtype=float32), array(0.03818933, dtype=float32)]
Epoch:70 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32), array(0.09919948, dtype=float32), array(0.08886633, dtype=float32), array(0.08059376, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32), array(0.04167863, dtype=float32), array(0.03818933, dtype=float32), array(0.0347609, dtype=float32)]
Epoch:80 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32), array(0.09919948, dtype=float32), array(0.08886633, dtype=float32), array(0.08059376, dtype=float32), array(0.07232123, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32), array(0.04167863, dtype=float32), array(0.03818933, dtype=float32), array(0.0347609, dtype=float32), array(0.03132383, dtype=float32)]
Epoch:90 | loss_test_value:[array(0.48106518, dtype=float32), array(0.3463552, dtype=float32), array(0.2172966, dtype=float32), array(0.14464018, dtype=float32), array(0.11360953, dtype=float32), array(0.09919948, dtype=float32), array(0.08886633, dtype=float32), array(0.08059376, dtype=float32), array(0.07232123, dtype=float32), array(0.06473556, dtype=float32)] | loss_train:[array(0.31288138, dtype=float32), array(0.19767132, dtype=float32), array(0.08908726, dtype=float32), array(0.05314853, dtype=float32), array(0.04543797, dtype=float32), array(0.04167863, dtype=float32), array(0.03818933, dtype=float32), array(0.0347609, dtype=float32), array(0.03132383, dtype=float32), array(0.0278874, dtype=float32)]
大家也可以把epochs先设置为1, 单独看看每一次的loss和模型的参数值,我是自己试过的,可以看到loss一直在变小,模型的参数在逐渐往真实值靠近,还蛮有趣的。
注意到这里有个zero_grad(),我刚开始也不知道它到底有什么作用,现在知道了,由于这是一个循环,那每次循环我们优化器中梯度就会累加,这样很明显是不利于我们进行参数学习的,因此我们使用**zero_grad()**对优化器的梯度进行一个清零的作用。
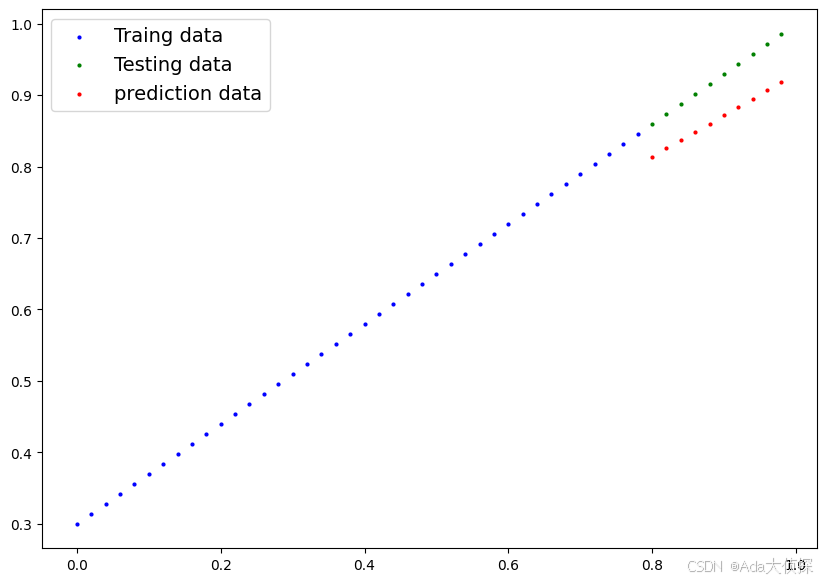
plot_predictions(predictions=y_test_preds)
哇哦,epochs=100,也就是说训练100次,我们的预测值就非常的接近真实值了,让我们来看看模型的参数是什么,是不是很接近真实值
print(f"model_0的参数:{model_0.state_dict()}")
print(f"实际的真实参数值:weights={weights}, bias={bias}")
model_0的参数:OrderedDict([(‘weights’, tensor([0.5784])), (‘bias’, tensor([0.3513]))])
实际的真实参数值:weights=0.7, bias=0.3
可以看出来,已经在慢慢接近了,证明方向是正确的,让咱们再来100次看看。再运行一次训练部分的代码即可。
# 开始正式写我们的训练部分了
epochs = 100
# 让我们定义一些容器来存储一些比较重要的内容,同时也可以方便我们画图和理解这些内涵
epoch_count = []
train_loss_values = []
test_loss_values = []
for epoch in range(epochs):
# 模型进入训练模式
model_0.train()
y_pred = model_0(X_train)
loss = loss_fn(y_pred, y_train)
# print(f"loss:{loss}")
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print(f"parameters:{model_0.state_dict()}")
# 模型进入评估模式
model_0.eval()
with torch.inference_mode():
test_pred = model_0(X_test)
test_loss = loss_fn(test_pred, y_test.type(torch.float))
if epoch % 10 == 0:
epoch_count.append(epoch)
test_loss_values.append(test_loss.detach().numpy())
train_loss_values.append(loss.detach().numpy())
print(f"Epoch:{epoch} | loss_test_value:{test_loss_values} | loss_train:{train_loss_values}")
Epoch:0 | loss_test_value:[array(0.05646304, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32)]
Epoch:10 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32)]
Epoch:20 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32)]
Epoch:30 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32)]
Epoch:40 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32)]
Epoch:50 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32), array(0.01647409, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32), array(0.00728353, dtype=float32)]
Epoch:60 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32), array(0.01647409, dtype=float32), array(0.00820156, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32), array(0.00728353, dtype=float32), array(0.00385178, dtype=float32)]
Epoch:70 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32), array(0.01647409, dtype=float32), array(0.00820156, dtype=float32), array(0.00502309, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32), array(0.00728353, dtype=float32), array(0.00385178, dtype=float32), array(0.00893248, dtype=float32)]
Epoch:80 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32), array(0.01647409, dtype=float32), array(0.00820156, dtype=float32), array(0.00502309, dtype=float32), array(0.00502309, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32), array(0.00728353, dtype=float32), array(0.00385178, dtype=float32), array(0.00893248, dtype=float32), array(0.00893248, dtype=float32)]
Epoch:90 | loss_test_value:[array(0.05646304, dtype=float32), array(0.0481905, dtype=float32), array(0.04060482, dtype=float32), array(0.03233228, dtype=float32), array(0.02405975, dtype=float32), array(0.01647409, dtype=float32), array(0.00820156, dtype=float32), array(0.00502309, dtype=float32), array(0.00502309, dtype=float32), array(0.00502309, dtype=float32)] | loss_train:[array(0.02445896, dtype=float32), array(0.02102021, dtype=float32), array(0.01758547, dtype=float32), array(0.01415539, dtype=float32), array(0.01071659, dtype=float32), array(0.00728353, dtype=float32), array(0.00385178, dtype=float32), array(0.00893248, dtype=float32), array(0.00893248, dtype=float32), array(0.00893248, dtype=float32)]
再运行一下这段代码就可以继续绘图了
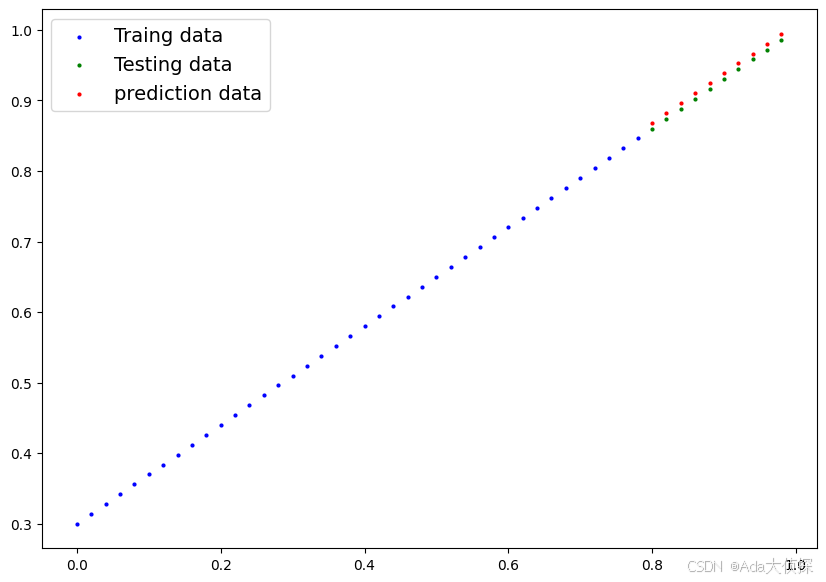
plot_predictions(predictions=y_test_preds)
哇,oh my god!又更加的接近了。再看看咱们的参数呢
print(f"model_0的参数:{model_0.state_dict()}")
print(f"实际的真实参数值:weights={weights}, bias={bias}")
model_0的参数:OrderedDict([(‘weights’, tensor([0.6990])), (‘bias’, tensor([0.3093]))])
实际的真实参数值:weights=0.7, bias=0.3
very close,非常接近了,BB们,兴不兴奋!
我们刚刚添加了测试的循环的代码,从model_0.eval()开始就是测试循环的代码啦!
现在我们开始尝试着绘画出损失函数的图像吧。
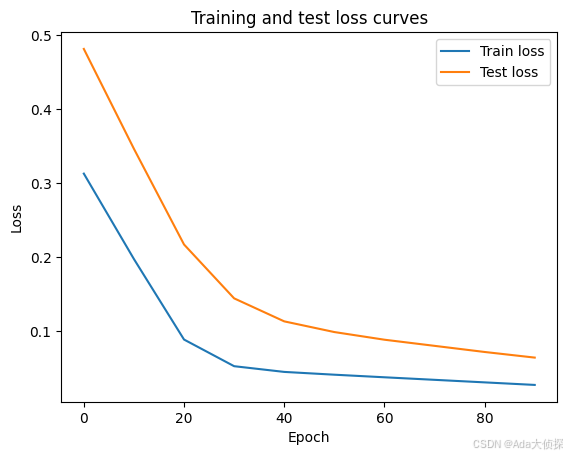
plt.plot(epoch_count, train_loss_values, label="Train loss")
plt.plot(epoch_count, test_loss_values, label="Test loss")
plt.title("Training and test loss curves")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
这是运行100次的损失图像,
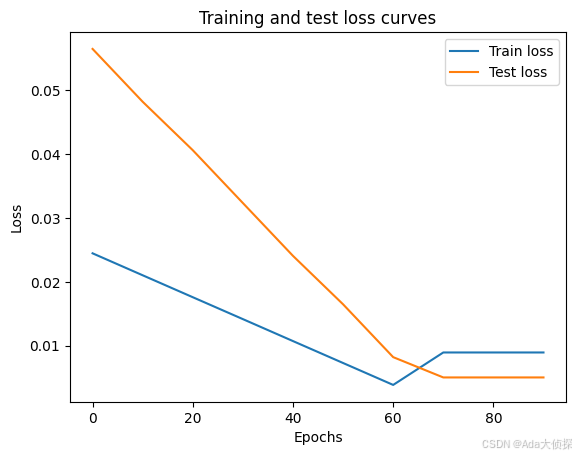
运行200次的损失图像如下,真的很奇怪,希望以后能懂得为什么会这个样子吧
好,今天真是收获满满,基本上是训练和测试过了一遍,而且咱们还进行了可视化,更加地了解我们的数据了
今天教二年级的小孩英语,他真的是不听,尊嘟快把我结节都气出来了。不生气不生气,人生就像一场戏
BB啊,我跟你说,今天中午吃的紫苏牛蛙,嘎嘎好吃,辣椒炒肉也很好吃,都吃撑了,很开心很开心
BB啊,如果我的文档对你有帮助的话,记得给俺点个赞呐~