前面介绍了$n$元语法模型，里面有一个叫隐状态，也被叫做隐藏变量，循环神经网络（recurrent neural networks，RNNs） 是具有隐状态的神经网络。

1 无隐状态的神经网络

以单隐藏层的多层感知机为例，设隐藏层的激活函数为$\varphi$，所以隐藏层的输出是：
$$\mathbf{H}=\varphi (\mathbf{X}{\mathbf{W}}_{xh}+{\mathbf{b}}_h).$$
然后把隐藏变量输入到输出层，则输出层的输出是：
$$\mathbf{O}=\mathbf{H}{\mathbf{W}}_{hq}+{\mathbf{b}}_q,$$

2 有隐状态的循环神经网络

我们用${\mathbf{H}}_t\in {\mathbb{R}}^{n\times h}$表示时间步$t$的隐藏变量，与多层感知机不同的是， 我们在这里保存了前一个时间步的隐藏变量${\mathbf{H}}_{t-1}$，并引入了一个新的权重参数${\mathbf{W}}_{hh}\in {\mathbb{R}}^{h\times h}$描述如何在当前时间步中使用前一个时间步的隐藏变量。

所以，当前时间步隐藏变量，由当前时间步的输入 与前一个时间步的隐藏变量一起计算得出：
$${\mathbf{H}}_t=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}+{\mathbf{b}}_h).$$
与无状态的神经网络相比，多了一个${\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}$，这些变量捕获并保留了序列直到其当前时间步的历史信息，就如当前时间步下神经网络的状态或记忆， 因此这样的隐藏变量被称为隐状态（hidden state）。

由于在当前时间步中， 隐状态使用的定义与前一个时间步中使用的定义相同， 因此计算是循环的（recurrent）。 于是基于循环计算的隐状态神经网络被命名为循环神经网络。 在循环神经网络中执行隐藏变量计算的层称为循环层。

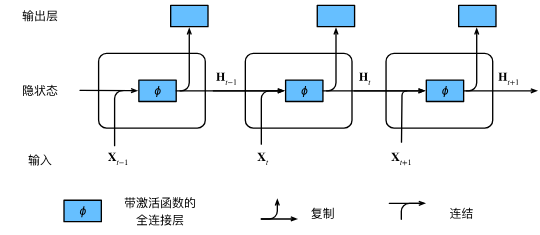
下图展示了循环神经网络在三个相邻时间步的计算逻辑。 在任意时间步$t$，隐状态的计算可以被视为：

1. 拼接当前时间步$t$输入${\mathbf{X}}_t$，和前一时间步$t-1$的隐状态${\mathbf{H}}_{t-1}$
2. 将拼接的结果送入带有激活函数$\varphi$的全连接层。 全连接层的输出是当前时间步$t$的隐状态${\mathbf{H}}_t$

3 基于循环神经网络的字符级语言模型

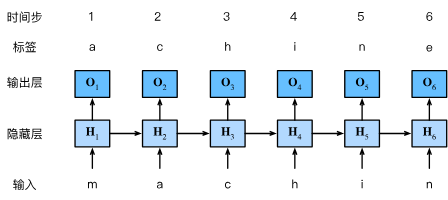
上一节提到，我们的目标是根据过去的和当前的词元预测下一个词元， 因此我们将原始序列移位一个词元作为标签。 Bengio等人首先提出使用神经网络进行语言建模，下图演示了如何通过基于字符级语言建模的循环神经网络， 使用当前的和先前的字符预测下一个字符。设小批量大小为1，批量中的文本序列为“machine”：

在训练过程中，我们对每个时间步的输出层的输出进行softmax操作， 然后利用交叉熵损失计算模型输出和标签之间的误差。

4 困惑度

如何度量语言模型的质量？由于历史原因，自然语言处理的科学家更喜欢使用一个叫做困惑度（perplexity） 的量，也就是一个序列中所有的$n$个词元的交叉熵损失的平均值的负指数：
$$\exp \left(-\frac{1}{n}\sum _{t=1}^n\log P(x_t\mid x_{t-1},\dots ,x_1)\right).$$
困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”:

• 在最好的情况下，模型总是完美地估计标签词元的概率为1。 在这种情况下，模型的困惑度为1。
• 在最坏的情况下，模型总是预测标签词元的概率为0。 在这种情况下，困惑度是正无穷大。
• 在基线上，该模型的预测是词表的所有可用词元上的均匀分布。 在这种情况下，困惑度等于词表中唯一词元的数量。 事实上，如果我们在没有任何压缩的情况下存储序列， 这将是我们能做的最好的编码方式。 因此，这种方式提供了一个重要的上限， 而任何实际模型都必须超越这个上限。