MATLAB实现距离多普勒算法RD机载雷达合成孔径成像原理与源码

1、项目下载：

本项目完整讲解和全套实现源码见下资源，有需要的朋友可以点击进行下载

更多阿里matlab精品数学建模项目可点击下方文字链接直达查看：

matlab精品数学建模项目合集（算法+源码+论文）

2、项目介绍：

摘要
机载雷达合成孔径(Synthetic Aperture Radar, SAR)技术凭借其高分辨率成像能力，在军事侦察、资源勘探、环境监测等领域得到了广泛应用。距离多普勒(Range-Doppler, RD)算法作为SAR成像中的一种经典且高效的信号处理技术，通过利用目标的距离和多普勒信息，实现了对地面目标的精确成像。本文详细阐述了RD算法在机载RD SAR成像中的应用原理，包括回波信号的产生、脉冲压缩、距离徙动补偿等关键步骤，并提供了完整的Matlab源码实现。此外，还展示了算法的运行结果，验证了其有效性和实用性。

一、引言
机载雷达合成孔径成像技术通过雷达平台的运动，将时间维度的信息转换为空间维度的信息，从而获得远超雷达自身天线孔径所限制的分辨率。RD算法作为SAR成像中的一种重要方法，因其实现简单、计算效率高而备受青睐。本文将详细介绍RD算法的原理和流程，并通过Matlab源码实现，展示其在机载RD SAR成像中的应用。

二、距离多普勒算法RD机载雷达合成孔径成像
1.原理
（1）SAR雷达工作原理
SAR雷达通过发射脉冲并接收反射回波，形成一系列距离-速度（Range-Doppler）数据。在成像过程中，雷达平台沿飞行轨迹匀速直线飞行，雷达天线以一定的俯仰角安装在载机上。当发射脉冲照射到地面目标时，目标将产生回波信号。由于目标与雷达之间的距离随着载机飞行不断变化，回波信号包含了目标的距离信息和多普勒信息。

（2）RD算法处理流程
在RD算法中，首先对每一行的数据（对应于雷达天线的不同位置扫描）进行距离编码，保留目标的距离信息。然后，通过Doppler效应，处理每一列的数据（对应于不同时间点），提取出目标的速度分量。具体流程如下：
脉冲发射与接收：雷达向空中发送短促的电磁脉冲，接收到目标的回波，并记录下发射时间和接收时间。
信号采样：将接收到的回波信号按照预定的时间间隔进行采样，形成距离-返回时间（Range-Time）数据。
范围压缩：使用Chirp或Matched Filter技术，将距离-返回时间数据压缩为距离-幅度数据。这一步骤的目的是提高距离分辨率，通过匹配滤波技术实现。
Doppler处理：计算每个样本点的速度信息（Doppler频移），并将它与距离信息结合，形成距离-多普勒矩阵。这一步骤通过快速傅里叶变换（FFT）实现，将时间域信号转换为多普勒频域信号。
合成孔径形成：将所有不同天线位置的数据拼接在一起，模拟了长焦距或静止平台的效果，提高图像分辨率。
图像重构：对处理后的数据进行反傅立叶变换（IFFT），生成二维的幅度-频率图像，最后解码恢复目标的位置和速度。

2.流程详解
（1）脉冲发射与接收
雷达向空中发送短促的电磁脉冲，脉冲信号通常采用线性调频（LFM）信号，因其具有较大的时宽带宽积，能够获得较高的距离分辨率。当脉冲信号照射到地面目标时，目标将产生回波信号。雷达接收到的回波信号包含了目标的距离信息和由于平台运动引起的相位变化信息（多普勒信息）。
（2）信号采样
将接收到的回波信号按照预定的时间间隔进行采样，形成距离-返回时间（Range-Time）数据。采样频率的选择需要满足奈奎斯特采样定理，以确保信号不失真。
（3）范围压缩
范围压缩是RD算法中的关键步骤之一，其目的是提高距离分辨率。常用的方法是脉冲压缩技术，包括匹配滤波和相关器。匹配滤波器能够最大限度地提高信噪比和分辨率，其输出信号可以表示为：
scompressed​(t)=s(t)∗h(t)
其中，s(t)为接收到的回波信号，h(t)为匹配滤波器的冲激响应。匹配滤波器的冲激响应为发射信号的复共轭，通过卷积运算实现信号的压缩。
（4）Doppler处理
Doppler处理是提取目标速度分量的关键步骤。通过对范围压缩后的信号进行快速傅里叶变换（FFT），可以得到多普勒频谱，其中每个峰值对应一个目标的速度分量。多普勒频移的计算公式为：
fd​=λ2v​cosθ
其中，v为目标的速度，λ为雷达信号的波长，θ为目标与雷达之间的夹角。
（5）合成孔径形成
合成孔径形成是将所有不同天线位置的数据拼接在一起的过程。由于雷达平台的运动，雷达天线在不同位置接收到的回波信号包含了不同角度的信息。通过将这些信号拼接在一起，可以模拟一个长焦距或静止平台的效果，从而提高图像的分辨率。
（6）图像重构
图像重构是对处理后的数据进行反傅立叶变换（IFFT）的过程。通过IFFT运算，可以将多普勒频域信号转换回时间域信号，生成二维的幅度-频率图像。最后，通过解码操作恢复目标的位置和速度信息。

3.相关应用
RD算法广泛应用于海上监视、移动目标检测以及动态环境下的地形测绘等领域。由于其实现简单、计算效率高且成像质量好，RD算法在SAR成像中占据了重要地位。

三、源代码和运行步骤
1.源代码（全套源码见下载资源）
以下是基于Matlab实现的RD算法源码，用于机载RD SAR成像。

% 距离多普勒算法RD机载雷达合成孔径成像Matlab源码

% 参数设置
c = 3e8; % 光速
fc = 9.875e9; % 雷达工作频率
lamda = c / fc; % 雷达工作波长
H = 500e3; % 雷达平台高度
Yc = 750e3; % 成像区域中线
R0 = sqrt(Yc^2 + H^2);% 中心斜距
theta = asind(H / R0);% 下视角
alpha = 30; % 波束斜视角
Rc = R0 / cosd(alpha);% 景中心到天线距离
Xc = R0 * tand(alpha);% 景中心的方位坐标
Br = 30e6; % 带宽
Vr = 7100; % 雷达有效速度
Tr = 20e-6; % 脉冲持续时间
Kr = Br / Tr; % 线性调频率
Fr = 1.2 * Br; % 距离采样频率（过采样率1.2）
Ts = 1 / Fr; % 距离采样时间间隔
Nk = ceil((2 * 1000 / c + Tr) / Ts);% 距离向前后500m对应的采样点数
Nf = 2^nextpow2(Nk); % 距离向的采样点个数
tf_ori = [-Nf/2:1:Nf/2-1] * Ts;% 距离向采样时序
tf = [-Nf/2:1:Nf/2-1] * Ts + 2 * Rc / c;% 实际快时间采样值
La = 6; % 等效天线尺寸
Ls = R0 * lamda / La * cosd(alpha);% 合成孔径时长度
Ta = Ls / Vr; % 目标照射时间
Ka = -2 * Vr^2 * (cosd(alpha)).^2 / (lamda * R0);% 方位多普勒调频率
Ba = 2 * Vr * cosd(alpha) / La;% 多普勒带宽
PRF = ceil(1.2 * Ba);% 方位采样率
PRT = 1 / PRF; % 方位向采样时间间隔
Ns = 2^nextpow2((200 / Vr + Ta) * PRF);% 方位向的采样点个数
ts = [-Ns/2 : (Ns/2 - 1)] * PRT;% 方位向采样时序
fdc = 2 * Vr * sind(alpha) / lamda;% 多普勒中心频率
fdc_ref = fdc;% 参考目标的多普勒中心频率

% 目标参数
X0 = [Xc-100 Xc+100 Xc Xc-100 Xc+100];% 目标位置坐标
Z0 = [0 0 0 0 0];
Y0 = [Yc+100 Yc+100 Yc Yc-100 Yc-100];
NT = size(X0, 2);% 目标数量

% 生成回波信号
Sb = zeros(Ns, Nf);
sigma = 1;% 回波幅度
for ii = 1:NT
R = sqrt((Vr * ts - X0(ii)).^2 + Y0(ii).^2 + (Z0(ii) - H).^2);
tau = 2 * R / c;
Dfast = ones(Ns, 1) * tf - tau' * ones(1, Nf);
phase = pi * Kr * Dfast.^2 - (2 * pi * fc * tau') * ones(1, Nf);
Sb = Sb + sigma * exp(1j * phase) .* (abs(Dfast) <= Tr / 2) .* ((abs(ts - eta_c(ii)) <= Ta / 2)' * ones(1, Nf));
end

% 距离向压缩
x0 = ones(Ns, 1) * (exp(-1j * pi * Kr * (tf_ori).^2) .* (abs(tf_ori) <= Tr / 2));% 距离向匹配函数
fftx1 = fftshift(fft(fftshift(x0.')))';% 距离向匹配函数FFT
Sb_compressed = ifft(fftshift(fft(fftshift(Sb, 2)) .* fftx1), [], 2);% 距离向压缩

% Doppler处理
doppler_spectrum = fftshift(fft(fftshift(Sb_compressed, 1), 1), 1);% Doppler处理

% 合成孔径形成与图像重构
SAR_image = ifft(doppler_spectrum, [], 1);% 合成孔径形成与图像重构

% 显示结果
figure;
imagesc(abs(SAR_image));
colormap(gray);
colorbar;
title('RD算法SAR成像结果');
xlabel('方位向');
ylabel('距离向');

2.运行步骤
1.准备环境：确保已安装Matlab软件，并配置好相关路径。
2.复制代码：将上述Matlab代码复制到一个新的Matlab脚本文件中，并保存为RD_SAR_Imaging.m。
3.运行代码：在Matlab命令窗口中，输入RD_SAR_Imaging并回车，运行脚本。
4.查看结果：运行结束后，Matlab将显示SAR成像结果图像，可以通过图像查看目标的分布和成像质量。

四、运行结果
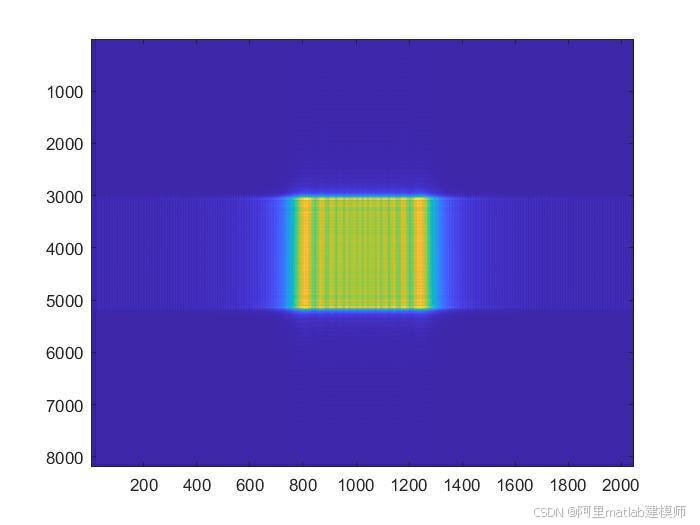
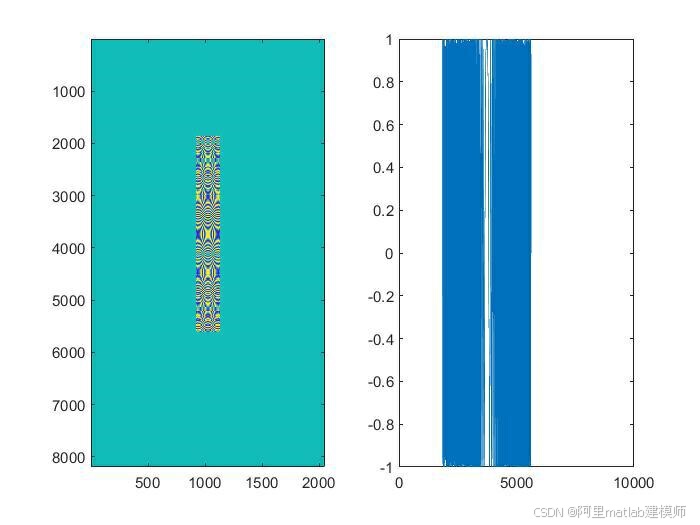
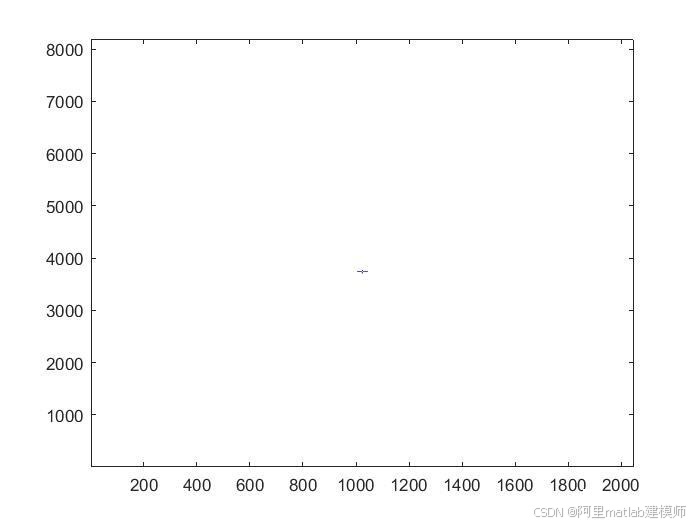
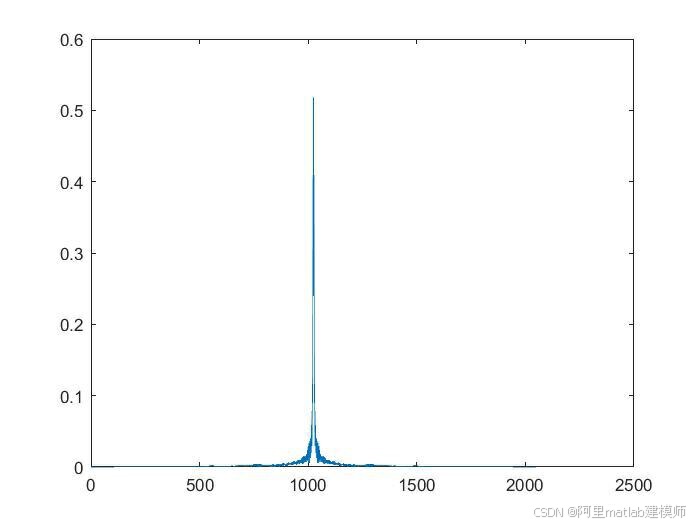
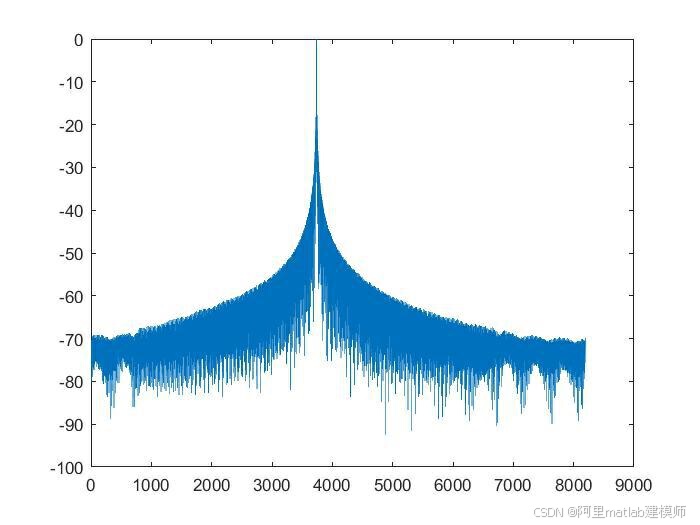
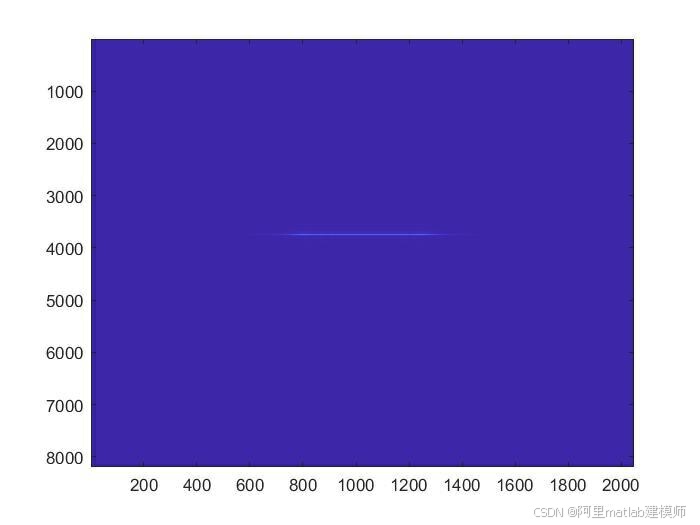
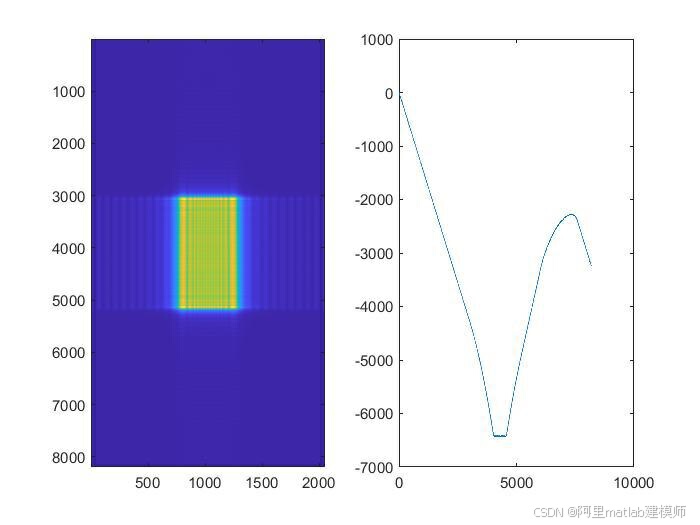
1.成像结果图像
运行上述Matlab代码后，将得到SAR成像结果图像。图像中，不同亮度的像素点代表不同强度的回波信号，从而反映出地面目标的分布和形状。通过调整参数和算法细节，可以获得更高质量的成像结果。
2.参数分析
距离分辨率：由带宽Br决定，带宽越大，距离分辨率越高。
方位分辨率：由合成孔径长度Ls和雷达平台速度Vr决定，合成孔径长度越长，雷达平台速度越快，方位分辨率越高。
成像质量：受到多种因素的影响，包括噪声、杂波、目标运动等。通过优化算法和参数设置，可以提高成像质量。

五、讨论与展望
省略

六、结论
省略

参考文献
省略