卷积运算
卷积运算是信号处理、图像处理和深度学习中的核心概念,用于表示两个函数之间的相互作用。它将一个函数通过滑动窗口的方式与另一个函数结合,产生一个新的函数,反映两者的重叠程度。
1. 定义
-
连续信号的卷积: 给定两个连续函数 f(t) 和 g(t) ,它们的卷积定义为:
其中:
- t 是输出信号的时间变量。
是中间变量,用于计算 f 和 g 的重叠。
-
离散信号的卷积: 给定两个离散序列 f[n] 和 g[n] ,它们的卷积定义为:
在实际计算中,信号长度通常有限,求和区间取有限范围。
2. 卷积运算的直观理解
卷积可以理解为:
- 将一个信号 g(t) 翻转后平移,与另一个信号 f(t) 逐点相乘并求和,得到新的信号。
- 在图像处理中,卷积用于提取特征,比如边缘检测、模糊化等。
卷积定理
卷积定理揭示了卷积运算在时域和频域之间的重要关系,是信号处理和傅里叶分析的重要理论。
1. 定理陈述
卷积定理说明:两个信号在时域中的卷积等价于它们在频域中的乘积。
-
连续信号的卷积定理: 如果 F(ω) 和 G(ω) 分别是 f(t) 和 g(t) 的傅里叶变换,则有:
即,时域卷积对应于频域相乘。
-
离散信号的卷积定理: 如果 F[k] 和 G[k] 分别是 f[n] 和 g[n] 的离散傅里叶变换(DFT),则:
同样,时域卷积等价于频域相乘。
2. 定理的逆向形式
卷积定理的逆向形式: 两个信号在频域中的卷积等价于它们在时域中的乘积:
卷积的计算示例
1. 离散卷积的计算
给定两个序列:
计算它们的离散卷积:
手动计算结果:
- 对 n=0 :
- 对 n=1 :
- 对 n=2 :
- 对 n=3 :
- 对 n=4 :
最终结果:
2. Python实现卷积
使用numpy库计算卷积:
import numpy as np
# 定义两个信号
f = np.array([1, 2, 3])
g = np.array([0, 1, 0.5])
# 计算卷积
result = np.convolve(f, g, mode='full')
print("卷积结果:", result)
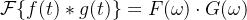
![\text{DFT}\{f[n] * g[n]\} = F[k] \cdot G[k]DFT](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN0ZXh0JTdCREZUJTdEJTVDJTdCZiU1Qm4lNUQlMjAqJTIwZyU1Qm4lNUQlNUMlN0QlMjAlM0QlMjBGJTVCayU1RCUyMCU1Q2Nkb3QlMjBHJTVCayU1RERGVA%3D%3D)
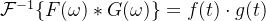
![f[n] = [1, 2, 3], \quad g[n] = [0, 1, 0.5]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9mJTVCbiU1RCUyMCUzRCUyMCU1QjElMkMlMjAyJTJDJTIwMyU1RCUyQyUyMCU1Q3F1YWQlMjBnJTVCbiU1RCUyMCUzRCUyMCU1QjAlMkMlMjAxJTJDJTIwMC41JTVE)
![(f * g) = [0, 1, 2.5,4, 1.5]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjhmJTIwKiUyMGclMjklMjAlM0QlMjAlNUIwJTJDJTIwMSUyQyUyMDIuNSUyQzQlMkMlMjAxLjUlNUQ%3D)