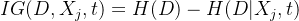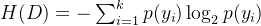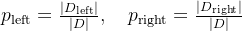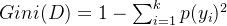如何构建多层决策树

构建一颗多层的决策树时，通过递归选择最佳划分特征（依据 信息增益 或 基尼系数）对数据集进行划分，直到满足停止条件（例如叶节点纯度达到要求或树的深度限制）。以下是基于 信息增益 和 基尼系数 的递推公式和推导过程：

1. 基于信息增益的递推公式与推导

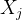
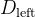
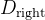
信息增益的目标是选择能够 最大化信息增益 的特征 X_j 和对应的分割点 t ，划分数据集 D 为 $D_{\text{left}}$ 和 $D_{\text{right}}$ 。

递推公式

信息增益计算公式：

信息增益定义为划分前后的信息熵差值：

IG(D, X_j, t) = H(D) - H(D|X_j, t)

H(D)：数据集 D 的信息熵。
：数据集 D 按特征 cc 和分割点 t 划分后的条件熵。

信息熵公式：

对于一个数据集 D（含 n 个样本，类别数为 k ），信息熵定义为：

$H(D) = -\sum_{i=1}^k p(y_i) \log_2 p(y_i)$

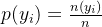
其中， $p(y_i) = \frac{n(y_i)}{n}$ ，即类别 y_i 的样本数占总样本数的比例。

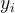
条件熵公式：

数据集 D 按特征 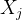X_j 和分割点 t 划分后：

左子集： $D_{\text{left}} = \{x \in D | X_j \leq t\}$
右子集： $D_{\text{right}} = \{x \in D | X_j > t\}$

条件熵为：

$H(D|X_j, t) = p_{\text{left}} H(D_{\text{left}}) + p_{\text{right}} H(D_{\text{right}})$

其中：

$p_{\text{left}} = \frac{|D_{\text{left}}|}{|D|}, \quad p_{\text{right}} = \frac{|D_{\text{right}}|}{|D|}$

递推推导过程

初始化根节点：
- 输入初始数据集 D 。
- 计算信息熵 H(D) 。
选择划分特征和分割点：
- 对每个特征和可能的分割点 t，计算信息增益： $IG(D, X_j, t) = H(D) - \left(p_{\text{left}} H(D_{\text{left}}) + p_{\text{right}} H(D_{\text{right}})\right)$
- 遍历所有特征和分割点，选择最大的和 t 。
递归划分：
- 使用最优特征和分割点 t 划分数据集：
  - 左子集 $D_{\text{left}}$
  - 右子集 $D_{\text{right}}$
- 对 $D_{\text{left}}$ 和 $D_{\text{right}}$ 重复上述过程，直到满足停止条件。

2. 基于基尼系数的递推公式与推导

CART 决策树使用 基尼指数 作为划分标准。目标是选择使 加权基尼系数最小 的特征 XjX_jXj 和分割点 t 。

递推公式

基尼系数公式：

对于数据集 D ，基尼系数定义为：

$Gini(D) = 1 - \sum_{i=1}^k p(y_i)^2$

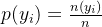
其中， $p(y_i) = \frac{n(y_i)}{n}$ 。

加权基尼指数公式：

数据集 D 按特征 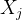X_j 和分割点 t 划分后，计算加权基尼指数：

$Gini(D|X_j, t) = p_{\text{left}} Gini(D_{\text{left}}) + p_{\text{right}} Gini(D_{\text{right}})$

其中：

$p_{\text{left}} = \frac{|D_{\text{left}}|}{|D|}, \quad p_{\text{right}} = \frac{|D_{\text{right}}|}{|D|}$

递推推导过程

初始化根节点：
- 输入初始数据集 D 。
- 计算基尼系数 Gini(D) 。
选择划分特征和分割点：
- 对每个特征和可能的分割点 t ，计算加权基尼指数： $Gini(D|X_j, t) = p_{\text{left}} Gini(D_{\text{left}}) + p_{\text{right}} Gini(D_{\text{right}})$
- 遍历所有特征和分割点，选择使最小的和 t 。
递归划分：
- 使用最优特征和分割点 t 划分数据集：
  - 左子集 $D_{\text{left}}$
  - 右子集 $D_{\text{right}}$
- 对 $D_{\text{left}}$ 和 $D_{\text{right}}$ 重复上述过程，直到满足停止条件。

3. 决策树构建停止条件

样本全部属于同一类别（纯度为 1）。
数据集不能再划分（没有剩余特征或达到深度限制）。
划分后的子集样本数太小，停止进一步划分。

4. 总结递推公式

信息增益递推公式：

$IG(D, X_j, t) = H(D) - \left(p_{\text{left}} H(D_{\text{left}}) + p_{\text{right}} H(D_{\text{right}})\right)$

基尼系数递推公式：

$Gini(D|X_j, t) = p_{\text{left}} Gini(D_{\text{left}}) + p_{\text{right}} Gini(D_{\text{right}})$

在决策树构建过程中，通过递归应用上述公式，选择最优的特征和分割点 t 来划分数据，最终构建完整的树。