一、实验目的
1、熟练掌握图的邻接矩阵和邻接表存储结构;
2、掌握图的创建方法;
3、掌握求顶点度的方法;
4、掌握图的深度优先和广度优先遍历方法;
5、掌握图的邻接矩阵和邻接表存储结构的转换。
二、实验内容
1、分别定义图的邻接矩阵和邻接表存储结构;
2、分别在两种存储结构下根据输入的顶点和边(或弧)创建图;
3、分别在两种存储结构下实现求顶点度的操作;
4、分别在两种存储结构下实现图的深度和广度优先遍历算法;
5、实现图的邻接矩阵和邻接表存储结构的转换。
三、实验步骤
1、定义图的存储结构
2、实现图的创建方法,并创建一个如下的图:
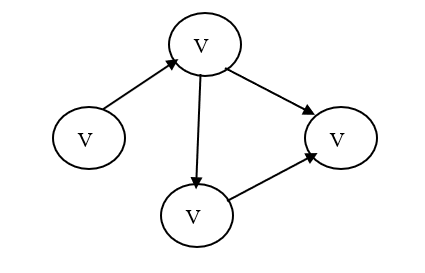
3、实现求第一个邻接点firstAdjVex()和下一个邻接点nextAdjVex()的操作;
4、写一个算法,求各个顶点的度;
5、对创建的图进行深度优先和广度优先遍历。
6、将邻接表存储的有向图转换为邻接矩阵或将邻接矩阵存储的图转换为邻接表。
四、代码及运行结果
import java.util.*;
public class ALGraph implements IGraph{
private GraphKind kind;
private int vexNum, arcNum;
public VNode[] vexs;
public ALGraph(GraphKind kind, int vexNum, int arcNum, VNode[] vexs) {
this.kind = kind;
this.arcNum = arcNum;
this.vexNum = vexNum;
this.vexs = vexs;
}
public ALGraph() {
this(null, 0, 0, null);
}
public void createGraph() {
Scanner sc = new Scanner(System.in);
System.out.println("请输入图的类型");
GraphKind kind = GraphKind.valueOf(sc.next());
switch (kind) {
case DG:
createDG();
return;
}
}
public void createDG() {
Scanner sc = new Scanner(System.in);
System.out.println("请分别输入图的顶点数,图的边数:");
vexNum = sc.nextInt();
arcNum = sc.nextInt();
vexs = new VNode[vexNum];
System.out.println("请分别输入图的各顶点:");
for (int v = 0; v < vexNum; v++) {
vexs[v] = new VNode(sc.next());
}
System.out.println("请输入各边顶点");
for (int k = 0; k < arcNum; k++) {
int v = locateVex(sc.next());
int u = locateVex(sc.next());
addArc(v, u);
}
}
public void addArc(int v, int u) {
ArcNode arc = new ArcNode(u);
arc.nextArc = vexs[v].firstArc;
vexs[v].firstArc = arc;
}
public int locateVex(Object vex) {
for (int v = 0; v < vexNum; v++)
if (vexs[v].data.equals(vex))
return v;
return -1;
}
public int getVexNum() {
return vexNum;
}
public int getArcNum() {
return arcNum;
}
public VNode[] getVexs(){
return vexs;
}
public GraphKind getKind(){
return kind;
}
public Object getVex(int v){
return vexs[v].data;
}
public Object nextAdjVex() {
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点及其一个邻接点求下一个邻接点");
Object V = sc.next();
Object W = sc.next();
int v = locateVex(V);
int w = locateVex(W);
try {
int s = nextAdjVex(v,w);
return vexs[s].data;
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public int nextAdjVex(int v, int w) throws Exception{
if (v<0&&v>=vexNum)
throw new Exception("不存在");
VNode vex=vexs[v];
ArcNode arcvw=null;
for (ArcNode arc=vex.firstArc;arc!=null;arc=arc.nextArc){
if (arc.adjVex==w){
arcvw=arc;
break;
}
}
if (arcvw!=null&&arcvw.nextArc!=null)
return arcvw.nextArc.adjVex;
else
return -1;
}
public Object firstAdjVex() {
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点求第一个邻接点");
Object V = sc.next();
int v = locateVex(V);
int w=firstAdjVex(v);
VNode vex=vexs[w];
return vex.data;
}
public int firstAdjVex(int v){
VNode vex=vexs[v];
if (vex.firstArc!=null)
return vex.firstArc.adjVex;
else
return -1;
}
//广度优先遍历
private static boolean[]visited;
public static void BFSTraverse(ALGraph G) {
visited = new boolean[G.getVexNum()];
for (int v=0;v<G.getVexNum();v++){
visited[v]=false;
}
for (int v=0;v<G.getVexNum();v++){
if(!visited[v])
BFS(G,v);
}
}
private static void BFS(ALGraph G,int v){
visited[v]=true;
System.out.print(G.getVex(v).toString()+" ");
LinkQueue Q=new LinkQueue();
Q.offer(v);
while(!Q.isEmpty()){
int u=(Integer)Q.poll();
try {
for(int w=G.firstAdjVex(u); w>=0; w=G.nextAdjVex(u,w))
if (visited[w]==false){
System.out.print(G.getVex(w).toString() +" ");
visited[w]=true;
Q.offer(w);
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
//深度优先遍历
public static void DFSTraverse(ALGraph G){
visited = new boolean[G.getVexNum()];
for (int v=0;v<G.getVexNum();v++){
visited[v]=false;
}
for (int v=0;v<G.getVexNum();v++){
if(!visited[v])
DFS(G,v);
}
}
private static void DFS(ALGraph G,int v) {
visited[v] = true;
System.out.print(G.getVex(v).toString() + " ");
try {
for(int w=G.firstAdjVex(v); w>=0; w=G.nextAdjVex(v,w))
if (visited[w]==false)
DFS(G,w);
} catch (Exception e) {
e.printStackTrace();
}
}
public int Degree(){
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点求度");
Object d = sc.next();
int v = locateVex(d);
return outDegree(v)+inDegree(v);
}
public int outDegree(int v) {
int count = 0;
for (ArcNode arc=vexs[v].firstArc;arc!=null;arc=arc.nextArc){
count++;
}
return count;
}
public int inDegree(int v) {
int count = 0;
for(int u = 0; u < vexNum; u++) {
for (ArcNode arc=vexs[u].firstArc;arc!=null;arc=arc.nextArc) {
if (arc.adjVex==v)
++count;
}
}
return count;
}
public void print(){
System.out.println("邻接表为");
for(int u = 0; u < vexNum; u++) {
System.out.print(vexs[u].data+"->");
for (ArcNode arc = vexs[u].firstArc; arc != null; arc = arc.nextArc) {
System.out.print(arc.adjVex+"->");
}
System.out.println();
}
}
public void exchange(ALGraph G) {
int vexNum,arcNum;
vexNum = G.getVexNum();
arcNum = G.getArcNum();
Object[] vexs;
int[][] arcs;
vexs = new Object[vexNum];
for (int v = 0; v < vexNum; v++) {
vexs[v] = G.vexs[v];
}
arcs = new int[vexNum][vexNum];
for (int v = 0; v < vexNum; v++) {
for (int u = 0; u < vexNum; u++) {
arcs[v][u] = 0;
}
}
for (int v=0; v < arcNum; v++) {
if (G.vexs[v].firstArc == null)
break;
else
for (ArcNode arc=G.vexs[v].firstArc;arc!=null;arc=arc.nextArc) {
arcs[v][arc.adjVex] = 1;
}
}
System.out.println("转化后邻接矩阵为");
for (int v = 0; v < vexNum; v++) {
for (int u = 0; u < vexNum; u++) {
System.out.print(arcs[v][u]+" ");
}
System.out.println();
}
}
}
public class ALGraphTest {
public static void main(String[] args) {
ALGraph t=new ALGraph();
t.createGraph();
t.print();
Object m=t.firstAdjVex();
System.out.println("第一个邻接点是"+m);
Object n = t.nextAdjVex();
System.out.println("下一个邻接点是"+n);
System.out.println("广度优先遍历结果为:");
ALGraph.BFSTraverse(t);
System.out.println();
System.out.println("深度优先遍历结果为:");
ALGraph.DFSTraverse(t);
System.out.println();
System.out.println("度为"+t.Degree());
t.exchange(t);
}
}
public class ArcNode {
public int adjVex;
public ArcNode nextArc;
public ArcNode(){
this(-1,null);
}
public ArcNode(int adjVex){
this(adjVex,null);
}
public ArcNode(int adjVex,ArcNode nextArc){
this.adjVex=adjVex;
this.nextArc=nextArc;
}
}
public enum GraphKind {
UDG,
DG,
UDN,
DN
}
public interface IGraph{
void createGraph();
int getVexNum();
int getArcNum();
Object getVex(int v);
int locateVex(Object vex);
int firstAdjVex(int v);
int nextAdjVex(int v,int w) throws Exception;
}
public interface IQueue<T> {
void clear();
boolean isEmpty();
int length();
T peek();
void offer(T x);
T poll();
}
//空队列时,size = 0 && front = null && rear = null
public class LinkQueue<T> implements IQueue<T> {
Node<T> front;
Node<T> rear;
int size;
static class Node<T> {
T data;
Node<T> next;
Node(T e, Node<T> p) {
data = e;
next = p;
}
}
public boolean isEmpty() {
return size == 0;
}
public int length() {
return size;
}
public T peek() {
if (front == null)
return null;
else
return front.data;
}
public void offer(T x) {
if (front == null) {
front = rear = new Node<>(x, null);
} else {
rear = rear.next = new Node<>(x, null);
// rear = rear.next;
}
size++;
}
public T poll() {
if (front == null)
return null;
else {
Node<T> p = front;
front = front.next;
T data = p.data;
p.data = null;
p.next = null;
size--;
if (front == null) {// 删除的是最后1个元素
rear = null;// front肯定是null
assert (size == 0);
}
return data;
}
}
public void clear() {
while (front != null) {
Node<T> p = front;
front = front.next;
p.data = null;
p.next = null;
}
size = 0;
rear = null;
}
public String toString() {
Node<T> p = front;
String result = getClass().getName() + ":";
while (p != null) {
result += p.data + " ";
p = p.next;
}
return result;
}
}public class LinkQueue2<T> implements IQueue<T> {
Node<T> front;
Node<T> rear;
int size;
static class Node<T> {
T data;
Node<T> next;
Node(T e, Node<T> p) {
data = e;
next = p;
}
}
public boolean isEmpty() {
return size == 0;
}
public int length() {
return size;
}
public T peek() {
if (size == 0)
return null;
else
return front.data;
}
public void offer(T x) {
if (size == 0) {
front = rear = new Node<>(x, null);
} else {
rear = rear.next = new Node<>(x, null);
//rear = rear.next;
}
size++;
}
public T poll() {
if (size == 0)
return null;
else {
Node<T> p = front;
front = front.next;
T data = p.data;
p.data = null;
p.next = null;
size--;
/*
if (size == 0) {// 删除的是最后1个元素,不要这一段也可以,因为总是用size==0判断队空
rear = null;// front肯定是null
assert (front == null);
}
*/
return data;
}
}
public void clear() {
for(; size != 0; --size) {//没有用front != null
Node<T> p = front;
front = front.next;
p.data = null;
p.next = null;
}
//size == 0,front == null, rear=?
}
public String toString() {
Node<T> p = front;
int i = size;
String result = getClass().getName() + ":";
while (i-- != 0) {
result += p.data + " ";
p = p.next;
}
return result;
}
}
import java.util.*;
public class MGraph {
public final static int INFINITY = Integer.MAX_VALUE;
private GraphKind kind;
private int vexNum, arcNum;
private Object[] vexs;
private int[][] arcs;
public MGraph(GraphKind kind, int vexNum, int arcNum, Object[] vexs, int[][] arcs) {
this.kind = kind;
this.vexNum = vexNum;
this.arcNum = arcNum;
this.vexs = vexs;
this.arcs = arcs;
}
public MGraph() {
this(null, 0, 0, null, null);
}
public void createGraph() {
Scanner sc = new Scanner(System.in);
System.out.println("请输入图的类型");
GraphKind kind = GraphKind.valueOf(sc.next());
switch (kind) {
case DG:
createDG();
return;
}
}
private void createDG() {
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点数,边数");
vexNum = sc.nextInt();
arcNum = sc.nextInt();
vexs = new Object[vexNum];
System.out.println("输入各个顶点");
for (int v = 0; v < vexNum; v++) {
vexs[v] = sc.next();
}
arcs = new int[vexNum][vexNum];
for (int v = 0; v < vexNum; v++) {
for (int u = 0; u < vexNum; u++) {
arcs[v][u] = 0;
}
}
System.out.println("输入矩阵为1的各个边的两个顶点");
for (int k=0; k < arcNum; k++) {
int v = locateVex(sc.next());
int u = locateVex(sc.next());
arcs[v][u] = 1;
}
}
public int locateVex(Object vex){
for(int v=0;v<vexNum;v++)
if(vexs[v].equals(vex))
return v;
return -1;
}
public Object getVex(int v){
return vexs[v];
}
//求第一个邻接点
/*
//第一种写法因为忘记已经给出的函数locateVex()而导致代码冗杂
public Object firstAdjVex(){
Scanner sc=new Scanner(System.in);
System.out.println("输入顶点");
Object V=sc.next();
int s;
for (int v = 0; v < vexNum; v++) {
if(vexs[v].equals(V)) {
try {
s=firstAdjVex(v);
return vexs[s];
} catch (Exception e) {
e.printStackTrace();
}
}
}
return null;
}
*/
//第二种写法使用了函数locateVex()
public Object firstAdjVex() {
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点求第一个邻接点");
Object V = sc.next();
int v = locateVex(V);
try {
int s=firstAdjVex(v);
return vexs[s];
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public int firstAdjVex(int v)throws Exception{
if(v<0&&v>=vexNum)
throw new Exception("不存在");
for (int j=0;j<vexNum;j++)
if (arcs[v][j]==1)
return j;
return -1;
}
//求下一个邻接点
public Object nextAdjVex() {
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点及其一个邻接点求下一个邻接点");
Object V = sc.next();
Object W = sc.next();
int v = locateVex(V);
int w = locateVex(W);
try {
int s=nextAdjVex(v,w);
return vexs[s];
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
public int nextAdjVex(int v,int w)throws Exception{
if (v<0 && v>=vexNum)
throw new Exception("不存在");
for (int j=w+1;j<vexNum;j++)
if (arcs[v][j]==1)
return j;
return -1;
}
//度
public int Degree(){
Scanner sc = new Scanner(System.in);
System.out.println("输入顶点求度");
Object d = sc.next();
int v = locateVex(d);
return outDegree(v)+inDegree(v);
}
//出度
public int outDegree() {
Scanner sc = new Scanner(System.in);
//System.out.println("输入顶点求出度");
Object a = sc.next();
int v = locateVex(a);
return outDegree(v);
}
public int outDegree(int v) {
int count = 0;
for(int i = 0 ; i < vexNum; i++) {
if(arcs[v][i] != 0 )
count++;
}
return count;
}
//入度
public int inDegree() {
Scanner sc = new Scanner(System.in);
//System.out.println("输入顶点求入度");
Object b = sc.next();
int v = locateVex(b);
return inDegree(v);
}
public int inDegree(int v) {
int count = 0;
for(int i = 0 ; i < vexNum; i++) {
if(arcs[i][v] != 0 )
count++;
}
return count;
}
//广度优先遍历
private static boolean[]visited;
public static void BFSTraverse(MGraph G) {
visited = new boolean[G.getVexNum()];
for (int v=0;v<G.getVexNum();v++){
visited[v]=false;
}
for (int v=0;v<G.getVexNum();v++){
if(!visited[v])
BFS(G,v);
}
}
private static void BFS(MGraph G,int v){
visited[v]=true;
System.out.print(G.getVex(v).toString()+" ");
LinkQueue Q=new LinkQueue();
Q.offer(v);
while(!Q.isEmpty()){
int u=(Integer)Q.poll();
try {
for(int w=G.firstAdjVex(u); w>=0; w=G.nextAdjVex(u,w))
if (visited[w]==false){
System.out.print(G.getVex(w).toString() +" ");
visited[w]=true;
Q.offer(w);
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
//深度优先遍历
public static void DFSTraverse(MGraph G){
visited = new boolean[G.getVexNum()];
for (int v=0;v<G.getVexNum();v++){
visited[v]=false;
}
for (int v=0;v<G.getVexNum();v++){
if(!visited[v])
DFS(G,v);
}
}
private static void DFS(MGraph G,int v) {
visited[v] = true;
System.out.print(G.getVex(v).toString() + " ");
try {
for(int w=G.firstAdjVex(v); w>=0; w=G.nextAdjVex(v,w))
if (visited[w]==false)
DFS(G,w);
} catch (Exception e) {
e.printStackTrace();
}
}
public GraphKind getKind(){
return kind;
}
public int[][] getArcs(){
return arcs;
}
public Object[] getVexs(){
return vexs;
}
public int getVexNum(){
return vexNum;
}
public int getArcNum(){
return arcNum;
}
//打印邻接矩阵检验
public void print(){
System.out.println("邻接矩阵为");
for (int v = 0; v < vexNum; v++) {
for (int u = 0; u < vexNum; u++) {
System.out.print(arcs[v][u]+" ");
}
System.out.println();
}
}
public void exchange(MGraph G) {
int vexNum, arcNum;
vexNum = G.getVexNum();
arcNum = G.getArcNum();
VNode[] vexs;
vexs = new VNode[vexNum];
for (int v = 0; v < vexNum; v++) {
vexs[v] = new VNode(G.vexs[v]);
}
for (int v = 0; v < arcNum; v++) {
for (int u = 0; u < arcNum; u++) {
if (arcs[v][u] == 1) {
ArcNode arc = new ArcNode(u);
arc.nextArc = vexs[v].firstArc;
vexs[v].firstArc = arc;
}
}
}
System.out.println("转换后的邻接表为");
for(int u = 0; u < vexNum; u++) {
System.out.print(vexs[u].data+"->");
for (ArcNode arc = vexs[u].firstArc; arc != null; arc = arc.nextArc) {
System.out.print(arc.adjVex+"->");
}
System.out.println();
}
}
}public class MGraphTest {
public static void main(String[] args){
MGraph t=new MGraph();
t.createGraph();
t.print();
System.out.println();
Object m=t.firstAdjVex();
System.out.println("该结点的第一个邻接点的是"+m);
Object n=t.nextAdjVex();
System.out.println("下一个邻接点是"+n);
System.out.println("此节点的度为"+t.Degree());
System.out.println("广度优先遍历结果为:");
MGraph.BFSTraverse(t);
System.out.println();
System.out.println("深度优先遍历结果为:");
MGraph.DFSTraverse(t);
System.out.println();
t.exchange(t);
}
}
public class VNode {
public Object data;
public ArcNode firstArc;
public VNode(){
this(null,null);
}
public VNode(Object data){
this(data,null);
}
public VNode(Object data,ArcNode firstArc){
this.data=data;
this.firstArc=firstArc;
}
}
运行结果:

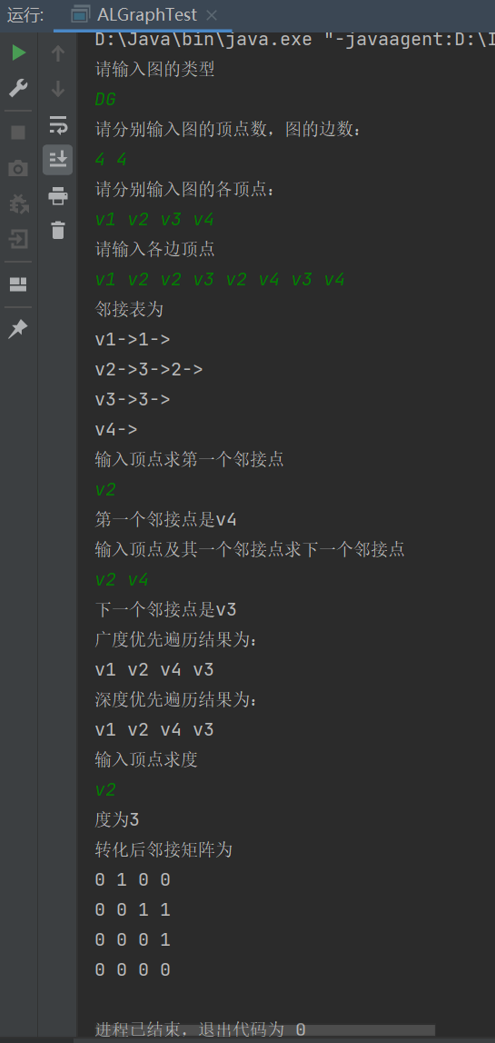
五、问题讨论
1、图的邻接矩阵和邻接表的存储结构各有什么特点?
邻接表特点:
(1)在无向图的邻接表中,顶点vi的度恰好等于该顶点的邻接表中边结点的个数;而在有向图中,顶点vi的邻接表中边结点的个数仅为该顶点的出度,若要求顶点的入度,则需遍历整个邻接表。有时为了便于求有向图中顶点的入度,可以通过建立一个有向图的逆邻接表得到,所谓逆邻接表,就是对图中的每个顶点vi建立一个链接以vi为终点的弧的边表。
(2)对于有n个顶点和e条边的无向图,其邻接表有n个顶点结点和2e个边结点,而对于有n个顶点和条弧的有向图,其邻接表有n个顶点结点和e个弧结点。显然,对于稀疏图,邻接表比邻接矩阵节省存储空间。
邻接矩阵特点:
用邻接矩阵存储图,虽然能很好地确定图中的任意两个顶点之间是否有边,但是不论是求任一顶点的度,还是查找任一顶点的邻接点,都需要访问对应的一行或一列中的所有的数据元素,其时间复杂度为O(n)。而要确定图中有多少条边,则必须按行对每个数据元素进行检测,花费的时间代价较大,其时间复杂度为O(n²)。从空间上看,不论图中的顶点之间是否有边,都要在邻接矩阵中保留存储空间,其空间复杂度为O(n²),空间效率较低,这也是邻接矩阵的局限性。
2、对于稀疏图和稠密图分别选择邻接矩阵和邻接表中的哪个存储更合适?
稀疏图邻接表更合适,稠密图邻接矩阵更合适。