背景概述
自从看了码农高天的python爱心代码就非常震撼,特别想了解其背后的实现原理,感觉是自己的知识不够,于是这股冲动带我刷了计算图形学,高数,线性,数值分析以及信号处理,最后发现然而并没什么用, 于是就开始静下心来从代码层面去剖析,终于把实现的过程了解了。这里不得不说,大佬就是大佬,你能理解但是你不一定能想出来。话不多说,下面就把代码以及注释贴在下面
代码及注释
加上空格一共204行代码
# 晚上星月争辉,美梦陪你入睡
import random
from math import sin, cos, pi, log
from tkinter import *
CANVAS_WIDTH = 640 # 画布的宽
CANVAS_HEIGHT = 480 # 画布的高
CANVAS_CENTER_X = CANVAS_WIDTH / 2 # 画布中心的X轴坐标
CANVAS_CENTER_Y = CANVAS_HEIGHT / 2 # 画布中心的Y轴坐标
IMAGE_ENLARGE = 11 # 放大比例
HEART_COLOR = "#ff2190"
def heart_function(t, shrink_ratio: float = IMAGE_ENLARGE):
"""
“只是绘制了心形线上的点,并没有任何其他效果”
“爱心函数生成器”
:param shrink_ratio: 放大比例
:param t: 参数
:return: 坐标
"""
# 原始xy用的float = IMAGE_ENLARGE,光环特效用的函数调用时传的实参,光环放大率11.6,心形11
x = 16 * (sin(t) ** 3) # 利用爱心函数公式计算x点坐标(极坐标公式?)
y = -(13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)) # 利用爱心函数公式计算y点坐标(极坐标公式?)
x *= shrink_ratio # x点放大11.6倍
y *= shrink_ratio # y点放大11.6倍
x += CANVAS_CENTER_X # 将x点加上画布一半的宽,其实是让图像在中心显示
y += CANVAS_CENTER_Y # 将y点加上画布一半的高
return int(x), int(y) # 返回整型的x,y点
def scatter_inside(x, y, beta=0.15): # beta:调用对象传递实参时就是实参,否则用形参定义的
"""
随机内部扩散
:param x: 原x
:param y: 原y
:param beta: 强度
:return: 新坐标
"""
ratio_x = - beta * log(random.random()) # random.random()随机生成0,1之间的浮点数,哈哈哈猜对了吧,每个点生成3个随机缩小的点
ratio_y = - beta * log(random.random()) # 随机不到的就是空白呗
'''
剩下的就简单了,为什么使用log函数,log函数默认以e为底(ln),
在对数[0,1]之间y取值极大概率落在[-100,0](比买彩票不中的概率还大,可以看一下函数曲线,然后看一下[0,1]对应的面积就知道了,大部分面积在[-1,0]之间),
加上-beta一个是让值为正,另一个是使3个点之间以及与x之间的差距不至于太大,beta=0.15,y也就是[0,0.15]
然后随机不到的地方就是空白啦
'''
'''
math.log() 方法语法如下:
math.log(x[, base])
参数说明:
x -- 必需,数字。如果 x 不是一个数字,返回 TypeError。如果值为 0 或负数,则返回 ValueError。
base -- 可选,底数,默认为 e。
'''
dx = ratio_x * (x - CANVAS_CENTER_X) # 对原始点进行概率缩小
dy = ratio_y * (y - CANVAS_CENTER_Y)
return x - dx, y - dy # 在画布中心的x,y在减去缩小的值返回
def shrink(x, y, ratio):
"""
抖动
:param x: 原x
:param y: 原y
:param ratio: 比例
:return: 新坐标
"""
# (x - CANVAS_CENTER_X) ** 2 + (y - CANVAS_CENTER_Y) ** 2) 是一个[0,+∞]的数 x的0.6次方是一个单调递增曲线,但是增幅不会特别大,1/x在[0,+∞]上单调递减,且大概率小于0.01
force = -1 / (((x - CANVAS_CENTER_X) ** 2 + (y - CANVAS_CENTER_Y) ** 2) ** 0.6) # 这个参数...
'原始x,y坐标的平方和开0.6次方'
dx = ratio * force * (x - CANVAS_CENTER_X) # 在原坐标基础上修改,作为跳动的新坐标
dy = ratio * force * (y - CANVAS_CENTER_Y)
return x - dx, y - dy # 在x,y坐标点上做微调,实现局部跳动现象
def curve(p):
"""
自定义曲线函数,调整跳动周期
:param p: 参数
:return: 正弦
"""
# 可以尝试换其他的动态函数,达到更有力量的效果(贝塞尔?)
return 2 * (2 * sin(4 * p)) / (2 * pi) # 先单调递增,然后单调递减,达到跳动效果
class Heart:
"""
爱心类
"""
def __init__(self, generate_frame=20):
self._points = set() # 原始爱心坐标集合
self._edge_diffusion_points = set() # 边缘扩散效果点坐标集合
self._center_diffusion_points = set() # 中心扩散效果点坐标集合
self.all_points = {} # 每帧动态点坐标 为了初始化这个变量可真不容易啊
self.build(2000) # 将2000传进self.build函数做计算,猜测得到self._points,self._edge_diffusion_points,self._center_diffusion_points,self.all_points坐标
self.random_halo = 1000
self.generate_frame = generate_frame
for frame in range(generate_frame): # 前面只是定义了静态的点,这里是动态的灵魂
self.calc(frame) # 将frame传入self.calc函数做计算
def build(self, number):
# 爱心
for _ in range(number): # 循环2000次
t = random.uniform(0, 2 * pi) # 生成0,2π之间的随机浮点数
x, y = heart_function(t) # 将0,2π之间的随机浮点数放入heart_function进行计算
self._points.add((x, y)) # 将整型的x,y点传给self._points,也就是传给原始爱心坐标集合
## 至此爱心轮廓已经画好
# 爱心内扩散
for _x, _y in list(self._points): # 取出x,y坐标
for _ in range(3): # 循环3次,猜测每个点生成缩小的3个点
x, y = scatter_inside(_x, _y, 0.05) # 将x,y,0.05传给scatter_inside函数,猜测是进行随机缩小点的定位
self._edge_diffusion_points.add((x, y)) # 将返回的随机三个x,y值传给self._edge_diffusion_points,也就是边缘扩散效果点坐标集合
## 至此内扩散轮廓已经画好
# 爱心内再次扩散
point_list = list(self._points) # 将self._points转换为列表
for _ in range(4000): # 循环4000次
x, y = random.choice(point_list) # 随机选择点
x, y = scatter_inside(x, y, 0.17) # x,y,0.17传给scatter_inside函数
self._center_diffusion_points.add((x, y)) # 将返回的随机三个x,y值传给self._center_diffusion_points,也就是中心扩散效果点坐标集合
@staticmethod
def calc_position(x, y, ratio):
# 调整缩放比例
force = 1 / (((x - CANVAS_CENTER_X) ** 2 + (y - CANVAS_CENTER_Y) ** 2) ** 0.520) # 魔法参数
dx = ratio * force * (x - CANVAS_CENTER_X) + random.randint(-1, 1) # 将原来在心形线上的点打散
dy = ratio * force * (y - CANVAS_CENTER_Y) + random.randint(-1, 1)
return x - dx, y - dy
def calc(self, generate_frame):
ratio = 10 * curve(generate_frame / 10 * pi) # 将实参传入curve进行计算,然后调参让跳动频率合适
halo_radius = int(4 + 6 * (1 + curve(generate_frame / 10 * pi))) # 外部光环计算
halo_number = int(3000 + 4000 * abs(curve(generate_frame / 10 * pi) ** 2))
all_points = []
# print(generate_frame / 10 * pi,ratio,halo_radius,halo_number)
# 光环
heart_halo_point = set() # 光环的点坐标集合
for _ in range(halo_number): # 循环3000-4500次不等,强化心形线上的点以及处理可能出现的重复点
t = random.uniform(0, 2 * pi) # 随机不到的地方造成爱心有缺口 返回0-2π之间的随机数
x, y = heart_function(t, shrink_ratio=11.6) # 魔法参数 将参数传递给heart_function
x, y = shrink(x, y, halo_radius) # 将x,y,半径传递给抖动函数shrink
if (x, y) not in heart_halo_point:
# 处理新的点
heart_halo_point.add((x, y))
x += random.randint(-14, 14)
y += random.randint(-14, 14)
size = random.choice((1, 2, 2))
all_points.append((x, y, size))
# 轮廓
for x, y in self._points:
x, y = self.calc_position(x, y, ratio)
size = random.randint(1, 3)
all_points.append((x, y, size))
# 内容
for x, y in self._edge_diffusion_points:
x, y = self.calc_position(x, y, ratio)
size = random.randint(1, 2)
all_points.append((x, y, size))
for x, y in self._center_diffusion_points:
x, y = self.calc_position(x, y, ratio)
size = random.randint(1, 2)
all_points.append((x, y, size))
self.all_points[generate_frame] = all_points
def render(self, render_canvas, render_frame): # 这里和上面没关系了,只是用到了self.generate_frame里面存储的内容
for x, y, size in self.all_points[render_frame % self.generate_frame]: # 调用self.all_points字典,% 取余 ,self.all_points里面有20个key,依次取出来。
render_canvas.create_rectangle(x, y, x + size, y + size, width=0, fill=HEART_COLOR) # 以矩阵的形式表示粒子化状态,牛啊!!!
def draw(main: Tk, render_canvas: Canvas, render_heart: Heart, render_frame=0):
render_canvas.delete('all') # 将之前的内容清除掉
render_heart.render(render_canvas, render_frame) # 调用Heart类里面的render方法
main.after(160, draw, main, render_canvas, render_heart, render_frame + 1) # 等待160ms之后继续调用draw函数,并且生成第二个渲染框
if __name__ == '__main__':
root = Tk() # 实例化Tk对象
canvas = Canvas(root, bg='black', height=CANVAS_HEIGHT, width=CANVAS_WIDTH) # 创建画布,传入root.windows,背景颜色,宽和高
canvas.pack() # 显示画框
heart = Heart() # 实例化爱心类
draw(root, canvas, heart) # 传入root.windows,画布和爱心函数开始画画
root.mainloop() # 一直显示画框
彩蛋
为了找到这个心形函数公式的出处,你猜我怎么做的?继续看:
我把多余的函数剔除了,只剩下生成静态爱心的公式,结果就是印证了我之前推理是正确的,But依旧没有找到这个公式。说多了都是泪,我去看看是不是极坐标转化为直角坐标来的。
# 晚上星月争辉,美梦陪你入睡
import random
from math import sin, cos, pi, log
from tkinter import *
CANVAS_WIDTH = 640 # 画布的宽
CANVAS_HEIGHT = 480 # 画布的高
CANVAS_CENTER_X = CANVAS_WIDTH / 2 # 画布中心的X轴坐标
CANVAS_CENTER_Y = CANVAS_HEIGHT / 2 # 画布中心的Y轴坐标
IMAGE_ENLARGE = 11 # 放大比例
HEART_COLOR = "#ff2190"
def heart_function(t, shrink_ratio: float = IMAGE_ENLARGE):
"""
“只是绘制了心形线上的点,并没有任何其他效果”
“爱心函数生成器”
:param shrink_ratio: 放大比例
:param t: 参数
:return: 坐标
"""
x = 16 * (sin(t) ** 3) # 利用爱心函数公式计算x点坐标(极坐标公式?)
y = -(13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)) # 利用爱心函数公式计算y点坐标(极坐标公式?)
x *= shrink_ratio # x点放大11.6倍
y *= shrink_ratio # y点放大11.6倍
x += CANVAS_CENTER_X # 将x点加上画布一半的宽,其实是让图像在中心显示
y += CANVAS_CENTER_Y # 将y点加上画布一半的高
return int(x), int(y) # 返回整型的x,y点
class Heart:
"""
爱心类
"""
def __init__(self, generate_frame=20):
self._points = set() # 原始爱心坐标集合
self._edge_diffusion_points = set() # 边缘扩散效果点坐标集合
self._center_diffusion_points = set() # 中心扩散效果点坐标集合
self.all_points = {} # 每帧动态点坐标 为了初始化这个变量可真不容易啊
self.build(2000) # 将2000传进self.build函数做计算,猜测得到self._points,self._edge_diffusion_points,self._center_diffusion_points,self.all_points坐标
self.random_halo = 1000
self.generate_frame = generate_frame
def build(self, number):
# 爱心
for _ in range(number): # 循环2000次
t = random.uniform(0, 2 * pi) # 生成0,2π之间的随机浮点数
x, y = heart_function(t) # 将0,2π之间的随机浮点数放入heart_function进行计算
size = random.randint(1,2)
self._points.add((x, y,size)) # 将整型的x,y点传给self._points,也就是传给原始爱心坐标集合
## 至此爱心轮廓已经画好
def render(self, render_canvas, render_frame): # 这里和上面没关系了,只是用到了self.generate_frame里面存储的内容
for x, y, size in list(self._points): # 调用self.all_points字典,% 取余 ,self.all_points里面有20个key,依次取出来。
render_canvas.create_rectangle(x, y, x + size, y + size, width=0, fill=HEART_COLOR) # 以矩阵的形式表示粒子化状态,牛啊!!!
def draw(main: Tk, render_canvas: Canvas, render_heart: Heart, render_frame=0):
render_canvas.delete('all') # 将之前的内容清除掉
render_heart.render(render_canvas, render_frame) # 调用Heart类里面的render方法
# main.after(160, draw, main, render_canvas, render_heart, render_frame + 1) # 等待160ms之后继续调用draw函数,并且生成第二个渲染框
if __name__ == '__main__':
root = Tk() # 实例化Tk对象
canvas = Canvas(root, bg='black', height=CANVAS_HEIGHT, width=CANVAS_WIDTH) # 创建画布,传入root.windows,背景颜色,宽和高
canvas.pack() # 显示画框
heart = Heart() # 实例化爱心类
draw(root, canvas, heart) # 传入root.windows,画布和爱心函数开始画画
root.mainloop() # 一直显示画框
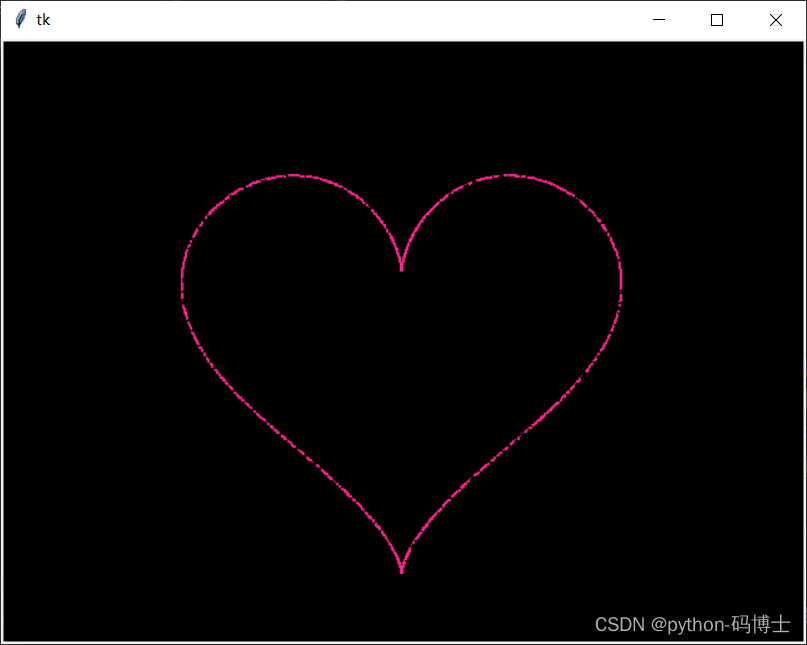
显示如下
完结
好吧,我还以为这个心形方程式是笛卡尔心形函数的某种变幻,其实没有关系,这是桃心形极坐标公式。