基本思想：回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。八皇后问题就是回溯算法的典型，第一步按照顺序放一个皇后，然后第二步符合要求放第2个皇后，如果没有位置符合要求，那么就要改变第一个皇后的位置，重新放第2个皇后的位置，直到找到符合条件的位置就可以了。是一种以深度优先搜索带以跳跃性搜索的算法。

回溯算法说白了就是穷举法，只不过在进行穷举的过程中，用剪枝函数跳过了一些不必要的搜索，跳过了一些不可能到达最终状态的子节点，减少状态空间树节点的生成

那么我们进行回溯算法比较疑惑的地方就是，何为状态空间树，状态空间树如何生成，如何根据问题找出非满足的状态，以及剪枝函数如何进行逻辑设定；

回溯法两种方式的伪代码：

1.递归回溯

void Backtrack(int t){
	if(t > n) Output(x);//Output 记录或者输出可行解
	else{
		for( int i = f(n,t); i <= g(n,t); ++i){//f(n,t)和g(n,t)表示在当前结点未搜索过的子树的起始编号和终止编号
			x[t] = h(i);
			if(constraint(t) && Bound(t)) Backtrack(t+1);//constraint和bound分别是约束函数和界限函数
		}
	}
}
递归实现回溯非常容易理解，但是执行效率没有迭代高，根据需要，开辟大量的内存空间，来进行递归。

2.迭代回溯：

void IterativeBacktrack(void){
 	int t = 1;
 	while(t > 0){
 		if(f(n,t) < g(n,t)){
 			for(int i = f(n,t); i <= g(n,t); ++i){//这个for 是遍历各个值的意思，实际中写成for循环会有逻辑错误
 				x[t] = h(i);
 				if(constraint(t) && bound(t)){
 					if(solution(t)) Output(x);//solution 判断是否已经得到问题的解
 					else t++;
 				}
 				else t--;
 			}
 		}
 	}
 }
 //迭代回溯相比较递归比较难理解，它的迭代过程就是解决问题的逻辑过程，不断进行循环，根据问题的规模，有时候时间复杂度也是不容乐观的。

为了个更好的理解回溯算法的原理，我们以解决n皇后问题为例：

举例：问题就是在 n×n 格的国际象棋上摆放n个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。
此问题如果用单纯的穷举法解决，会搜索出n^n个搜索结果，穷举的时候从所有皇后都放在第 1 行的方案开始，检验皇后之间是否会相互攻击。如果会，把列 H 的皇后挪一格，验证下一个方案。移到底了就 “进位” 到列 G 的皇后挪一格，列 H 的皇后重新试过全部的 n 行，毫无疑问这种方法效率极低，n过大的话直接会把计算机给跑死，所以我们来看回溯算法。

讲算法之前先展示一下何为状态空间树；

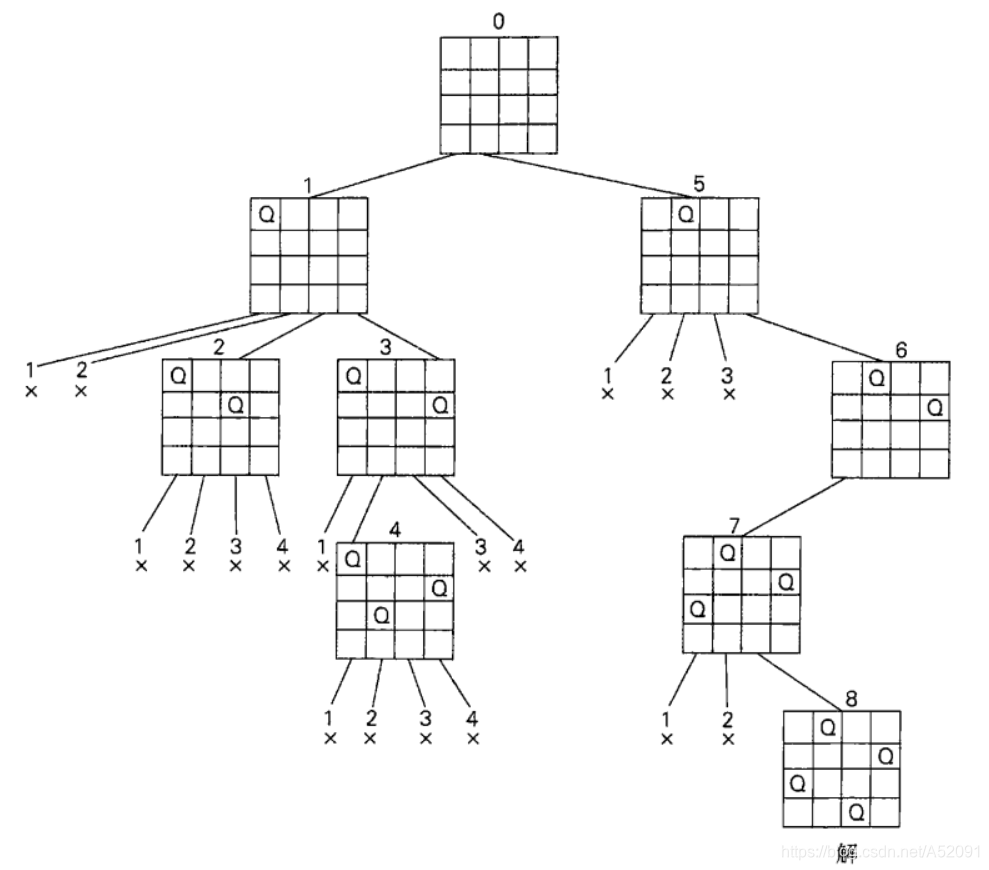
这里我们以四皇后问题解释一下何为状态空间树：

以一个4×4的空棋盘为根，先在棋盘的第一行第一列（1，1）处放置一个皇后1，然后观察皇后2的情况，对于皇后2，在第一列和第二列都无法放置，那么尝试第三列，当我们放置皇后2在（2，3）处时，发现皇后3无法放置，进入了死路，这时候我们进行回溯，将皇后2放置在第四列，然后发现皇后3可以放在（3，2）的这个位置，但是此时问题又出现了，皇后4无法防止，进入死路，那么我们继续回溯，回溯到皇后1应当放置的位置，将皇后1放置在第二列，依次类推，直到找到最后的可成立的一个放置解。这就是该算法的搜索状态空间树。
但是以上的只是一部分，仅仅是皇后1到达第二列为止，其他的方式还可以有搜索状态，但是总的思路是一致的。

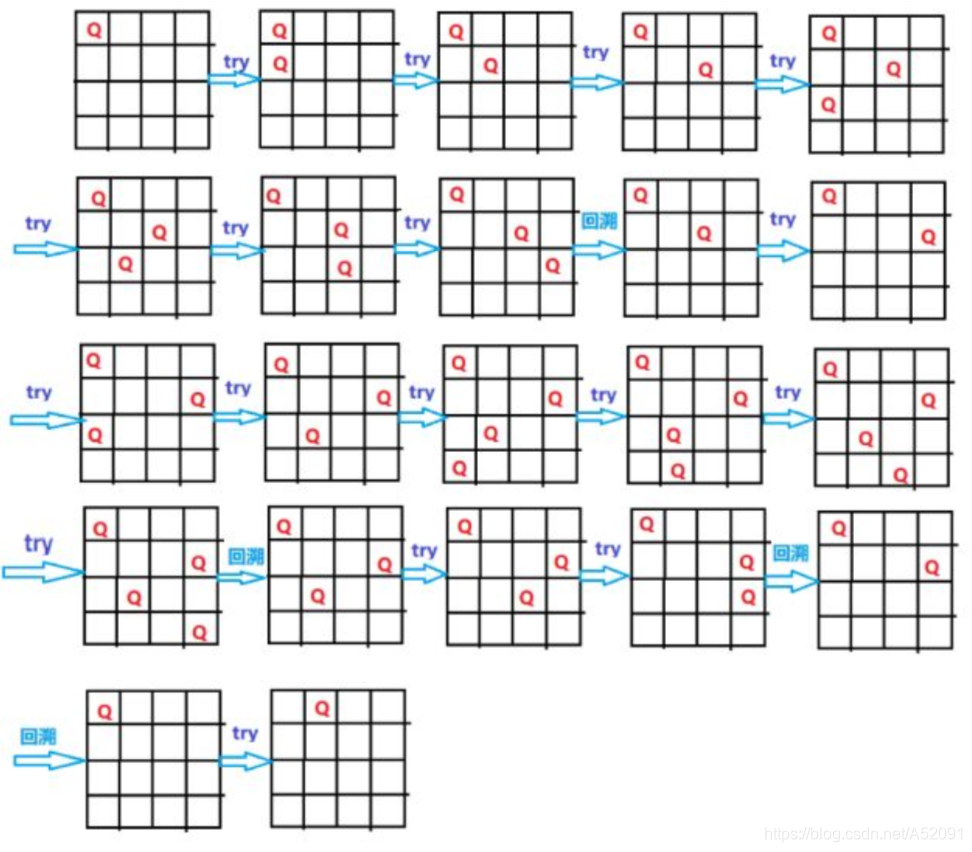
进行搜索的过程如下（以四皇后为例）

解决皇后问题比较开心的就是，他的状态空间树的每一个节点就是一个二维空间，代码实现的时候，可以很清晰的进行每一步的搜索，符合计算机存储的逻辑。
到这里我们实际上已经搞清楚了，不满足的状态就是，在每一个皇后位置，同行同列对角线即为不满足，我们搜索的过程一旦遇到此种状态，在进行一步步的搜索时，就要用剪枝函数（此题中就是一个if判断）来进行跳跃回溯搜索。

综上我们大致搞清楚了，进行回溯的时候，回溯到底是一个什么逻辑，回溯难在你需要对问题足够的清晰，搞清楚你这个空间树是子集树还是排序树，亦或者其他，在进行代码实现的时候如何模拟你的搜索过程，采取哪种数据结构，运用递归还是迭代实现过程。（常见的比较难的问题时，可以先写一个递归的伪代码，一般是比较容易想出来的，然后在伪代码基础上进行修改）这是我们大体上的解决过程。总归回溯这种思想是很简明易懂的，但是回溯解决问题的时候，代码实现还是有一定的距离的，这就需要我们大量面对问题，多做多练。

代码实现：
这里只进行了迭代回溯
 

#include<stdio.h>
#include<iostream> 
#include<cmath>
using namespace std;
//用一维数组存储，解决行冲突，数组下标为行数，数组值为列数 
int x[10]={0};
int count=0;
bool judge(int k)//判断第k行某个皇后是否发生冲突 ，发生冲突就跳过
{
    int i=1;
    while(i<k)  //循环i到k-1之前的皇后； 
    { 
        if(x[i]==x[k]||abs(x[i]-x[k])==abs(i-k))//存在列冲突或者存在对角线冲突（实际上就是一种剪枝）
            return false;
        i++;
    }
    return true;
}
void queen(int n)
{
    int i,k=1; //k为当前行号，从第一行开始 
    x[1]=0;//x[k]为第k行皇后所放的列号
    while(k>0)
    {
        x[k]++;  //首先从第一列开始判断 
        while(x[k]<=n&&!judge(k))//推导k行到底选择哪一列，如果当前该列不行则下一列，直到成立即可； 
          x[k]++;
        if(x[k]<=n)  
        {
            if(k==n)//输出所有解 
            {
                for(i=1;i<=n;i++)
                    printf("第%d行的皇后：在第%d列  ",i,x[i]);
                count++;
                printf("-------这是其中第%d个解",count);   
                printf("\n");
            }

            else//判断下一行
            {
                k++; x[k]=0;
            }
        }
        else k--;//没找到，回溯
    }
    return ;
}
int main()
{
    int n;
    cout<<"请输入你的n皇后：     "; 
    cin>>n;//n最大值不超过10 
    queen(n);
    return 0;
}