功能包括平滑与求导

函数如下

function [X_total, smooth_data] = Savitzky_Golay_filter_temp(data, dt, framelen, order)
% X_total [a_0, a_1, a_2]
% 输入序列、序列间隔、滑窗长度、拟合阶数
% 返回平滑值 & 阶参数
% Y = AX - B

% 形成 B 矩阵
B_total = struct() ;
total_num = length(data) - framelen + 1 ;
for i = 1 : total_num
    B = zeros(framelen, 1) ;
    B(:, 1) = data(i: i + framelen - 1) ;
    B_total(i).B = B ;
end

% 形成 A 矩阵
A_total = struct() ;
for i = 1 : total_num
    A = [] ;
    for j = 0 : order
        A_temp = linspace(-(framelen - 1)/2*dt, (framelen - 1)/2*dt, framelen).^(j) ;
        A(:, j + 1) = A_temp ;
    end
    A_total(i).A = A ;
end

% 形成最小二乘解 & 滤波值
X_total = [] ; % 系数矩阵
Y_hat_total = struct() ;
smooth_data = zeros(1, length(data)) ;
for i = 1 : total_num
    B = B_total(i).B ;
    A = A_total(i).A ;
    X = inv(A' * A) * A' * B ;
    X_total = [X_total; X'] ;
    Y_hat = A * X ;
    Y_hat_total(i).Y_hat = Y_hat ;

    switch i
        case 1
            smooth_data(1: (framelen - 1)/2 + 1) = Y_hat_total(i).Y_hat(1: (framelen - 1)/2 + 1) ;
        case total_num
            smooth_data(end - (framelen - 1)/2: end) = Y_hat_total(i).Y_hat(1 + (framelen - 1)/2: end) ;
        otherwise
            smooth_data((framelen - 1)/2 + i) = Y_hat_total(i).Y_hat(1 + (framelen - 1)/2) ;
    end

end

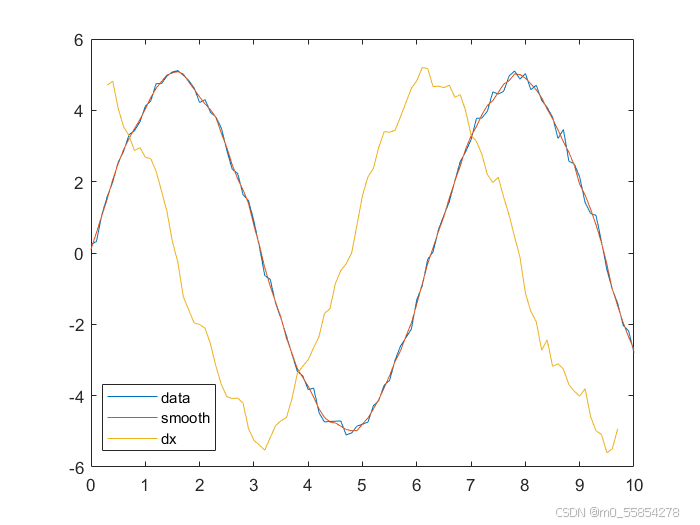
测试效果

clear all
clc
t = 0: 0.1: 10 ;
data_gen = @(t) 5 * sin(t) ;
noise = 0.2 * randn(1, length(t)) ;
data = data_gen(t) + noise;
plot(t, data)
hold on
[X_total, smooth_data] = Savitzky_Golay_filter_temp(data, 0.1, 7, 2) ;
plot(t, smooth_data)
plot(t(4: end - 3), X_total(:, 2))
legend('data', 'smooth', 'dx')

结果图片