前言:
今天,我给大家讲解的是关于全排列算。我会从三个方面去进行展开:
- 首先,我会给大家分析关于全排列算法的思想和定义;
- 紧接着通过手动实现出一个全排列代码来带大家见见是怎么实现的;
- 最后我会给出两道题帮助大家去进行理解记忆。
目录
前情摘要
- 在今后的找工作中,全排列相对来说还是一个比较常见问题。不管是不是做算法岗的,在许多的大公司面试中都会考察应聘者有关全排列的问题(就算不让你编写完整代码,也会让你描述大致的思路)。接下来,我就带领大家去学习有关全排列的相关知识。
(一)定义和公式讲解
1、定义
- 全排列就是从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。
- 当m=n时所有的排列情况叫全排列。
- 简单点来说就是:全排列的含义就是一个序列所有的排序可能性
我们通过简单的举例带大家直观的认识一下:
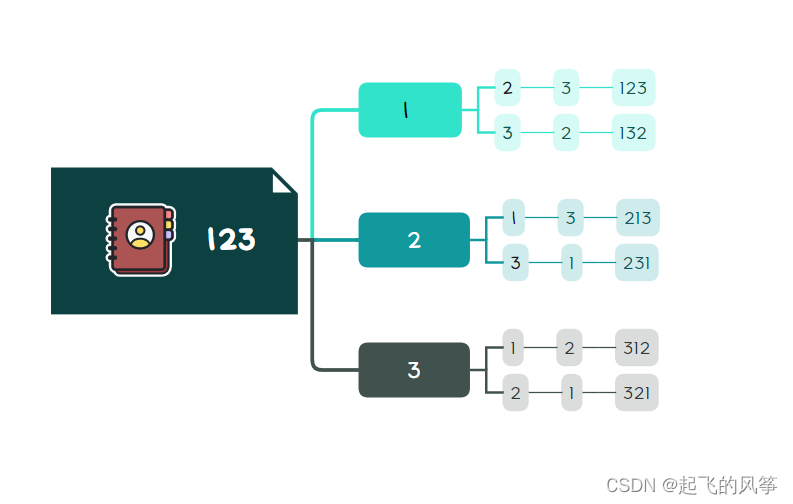
💨 假设现在数组中有【1 2 3】这样的三个元素,那么对其进行排列之后结果是什么呢?
我相信聪明的小伙伴们已经知道答案了,具体的如下:
- 123
- 132
- 213
- 231
- 321
- 312
💨 假设现在数组中有【1 2 3 4】这样的四个元素,那么对其进行排列之后结果是什么呢?
具体的如下:
- 1234
- 1243
- 1324
- 1342
- 1432
- 1423
- 2134
- 2143
- 2314
- 2341
- 2431
- 2413
- 3214
- 3241
- 3124
- 3142
- 3412
- 3421
- 4231
- 4213
- 4321
- 4312
- 4132
- 4123
2、公式
因此,综上所述,我们可以发现全排列得到的结果的数量跟数学中的全排列问题是一样的
- 对于给定的序列,假设序列中 N个元素,对其进行全排列之后我们可以得到的排序数量为 N!
(二)全排列的初始思想
1、上述我给出了一个序列的全排列的结果以及全排列得到的最终的结果数量。
2、接下来,我简单的讲述一下上述全排列是如何得到的,对其具体的实现过程进行描述。
💨 具体过程如下:
- 1、我们以上述数组中的【1 2 3 4】,这里是排序好的,为了更好的说明,我们以【2 1 3 4】为例;
- 2、首先,我们先保持第一个元素不变,即【2】不变,对数组中剩余的元素【1 3 4】进行排序;
- 3、同上,继续上述过程。此时我们保持剩余数组中的【1】不变,对【3 4】进行排序;
- 4、在往下遍历。保持【3】不变,对【4】对进行全排列,由于【4】只有一个,它的排列只有一种:4。因此上述完成之后我们可以得到一种排序结果,即【2 1 3 4】;
- 5、接下来因为【4】已经遍历过,所以不能在以【4】打头了。此时需要交换【3 4】这两个元素的位置,得到新的一种排序,即【2 1 4 3】 ;
- 6、完成上述的操作之后,此时【3 4】的情况都写完了,现在进行回溯,则不能以【1】打头了;
- 7、所以现在我们需要交换的对象就是【1 3】,依次类推,最终我们可以得到以【2】开头的排列有以下几种:
2134
2143
2314
2341
2431
2413- 8、在接下来就是改变第一个位置的元素,即通过剩余的【 1 3 4 】作为头元素,在重复上述过程即可得到最终的全排列结果。
(三)代码实现
通过上述的分析,我们不难发现一个问题那就是:
- 对于给定的序列,刚开始时我们知道序列的第一个元素,剩余的序列元素此时又可以看成是一个全排列的例子;
- 我们可以对剩余的序列进行与开始相同的操作,直到中只一个元素为止。这样我们就获得了所有的可能性。因此不难看出这是一个递归的过程。
接下来,我们简单的实现一下这样的代码:
1、递归不去重
- 思路如下:
- 求n位的字符串的全排列,先确定第0位,然后对后面n-1位进行全排列,在对n-1为进行全排列时,先确定第1位,然后对后面的n-2位进行全排列,...由此得到递归函数和递归的结束条件;
- 因此解决n-1位元素的全排列就能解决n位元素的全排列了。
- 代码如下:
//生成向量的所有排列
void permute(string str, int left, int right)
{
//如果遍历到 left == right ,说明全排列已经做完了只需输出即可
if (left == right)
cout<<str<<endl;
else {
// 递归情况:生成剩余元素的排列
for (int i = left; i <= right; i++)
{
// 将当前元素与第一个元素交换
//保持第一个元素固定并生成其余元素的排列
swap(str[left], str[i]);
// 递归调用
permute(str, left+1, right);
//进行回溯
swap(str[left], str[i]);
}
}
}
int main()
{
string str = "211";
int size = str.size();
permute(str, 0, size-1);
return 0;
}💨 上面的程序乍一看没有任何问题了。但是当我们去想去打印输出时,看看运行的结果会怎么样:
- 结果如下:
- 现象解释:
- 从上我们可以发现出现了好多的重复。
- 重复的原因当然是因为我们列举了所有位置上的可能性,而没有太多地关注其可能存在重复的数值。
2、递归去重
那么此时很多小伙伴就要问了,我们想实现去重的排列可不可以呢?答案当然是可以的。具体如下:
- 思路如下:
去重跟不去重相差的其实就是对于元素的值的比较,我们设置一个 flag 标志位,来判断当前元素之后的元素是否于当前元素相同,再利用标志位去对其设限即可实现递归去重操作。
- 代码如下:
void generatePermute(vector<int>& arry, int start, vector<vector<int>>& tmp)
{
if (start == arry.size()) {
tmp.push_back(arry);
return;
}
for (int i = start; i < arry.size(); i++) {
// 检查与前一个元素的交换是否会产生重复项
bool flag = false;
for (int j = start; j < i; j++) {
if (arry[i] == arry[j]) {
flag = true;
break;
}
}
if (!flag) {
swap(arry[start], arry[i]);
generatePermute(arry, start+1, tmp);
swap(arry[start], arry[i]);
}
}
}
vector<vector<int>> permute(vector<int>& arry)
{
vector<vector<int>> tmp;
sort(arry.begin(), arry.end());
generatePermute(arry, 0, tmp);
return tmp;
}
int main()
{
vector<int> arry = {1, 1, 2};
vector<vector<int>> res = permute(arry);
for (auto& e1 : res)
{
for (auto& e2 : e1)
{
cout << e2 << " ";
}
cout << endl;
}
return 0;
}- 运行结果:
💨 我们在把 arry数组中的元素换为【1 2 2】,看最终结果是否正确,具体如下:
- 代码解释:
- 上述实现生成了输入向量 arry 的所有排列,同时避免了重复。
-
permute 函数首先对输入向量进行排序,以将相同值的元素分组在一起。
- 然后,它调用 generatePermute函数,以递归方式生成从给定索引开始的所有排列。generatePermute函数将当前索引处的元素与所有后续元素交换以生成排列,同时还检查与以前交换的元素的重复项。
3、非递归实现
由于非递归的方法是基于对元素大小关系进行比较而实现的,所以这里暂时不考虑存在相同数据的情况。
- 代码如下:
void permute(vector<int>& arry)
{
sort(arry.begin(), arry.end());
stack<pair<int, int>> tmp;
tmp.push({-1, 0});
while (!tmp.empty())
{
int i = tmp.top().first, j = tmp.top().second;
tmp.pop();
if (i >= 0)
swap(arry[i], arry[j]);
if (j == arry.size() - 1) {
// 输出排列
for (int k = 0; k < arry.size(); k++)
{
cout << arry[k] << " ";
}
cout << endl;
}
else
{
for (int k = arry.size() - 1; k > j; k--)
{
tmp.push({j, k});
}
tmp.push({-1, j+1});
}
}
}
int main()
{
vector<int> arry = {0,2,2};
permute(arry);
return 0;
}- 代码解释:
- main() 函数创建一个包含三个元素的向量 arry,并以 arry 作为输入调用 permute() 函数;
- 首先,函数void permute(vector<int>&arry)将整数向量的引用作为输入,该向量使用STL中的sort()函数按升序排序;
- 其次,维护一堆整数对 {i,j},其中 i 和 j 是数组 arry 的索引;
- 最初,堆栈包含对 {-1, 0};
- 然后,该算法从堆栈中重复弹出顶部对,通过交换索引 i 和 j 处的元素来更新 arry(如果 i >= 0),并将新对推送到堆栈上;
- 最后,当栈中元素全被弹出,栈顶和栈底相遇,则所有状态全被穷尽。arry 的所有排列都已生成并打印到标准输出。
(四)题目讲解
接下来,我通过LeetCode上的三道题目给大家练练手,帮助大家理解记忆!!!
1、字符串的排列
链接如下:字符串的排列
💨 题目如下:
💨 思路讲解:
- 上述我们是通过数组求全排列,而本题是字符串进行相关操作;
- 其实字符串与数组没有区别,一个是数字全排列,一个是字符全排列,因此大致思路与上述是类似;
- 为了便于后序去重,我们先优先按照字典序排序,因为排序后重复的字符就会相邻,后续递归找起来也很方便;
- 首先使用临时变量去组装一个排列的情况:每当我们选取一个字符以后,就确定了其位置,相当于对字符串中剩下的元素进行全排列添加在该元素后面,给剩余部分进行全排列就是一个子问题,因此可以使用递归;
💨 代码展示:
class Solution {
public:
vector<int> arry;
vector<string> res;
void dfs(const string &s, int num, string &tmp)
{
//临时字符串满了加入输出
if(num == s.size())
{
res.push_back(tmp);
return;
}
//遍历所有元素选取一个加入
for(int i=0; i<s.size(); ++i)
{
if(arry[i] == 0)
{
tmp+=s[i];
arry[i]=1;
dfs(s,num+1,tmp);
arry[i] = 0;
tmp.pop_back();
while(i<s.size()-1 && s[i] == s[i+1])
i++;
}
}
}
vector<string> permutation(string s) {
//先对字符串进行排序处理
sort(s.begin(), s.end());
//标记每个位置的字符是否被使用过s
string tmp;
arry=vector<int>(s.size());
dfs(s,0,tmp);
return res;
}
};💨 代码解释:
1️⃣ 首先优先按照字典顺序进行排序;
2️⃣ 创建一个 arry 数组标记字典中的字母是否被选择;
3️⃣紧接着就进入dfs 函数进行递归操作;
4️⃣写出递归的条件:
①如果填充的字符串已经到达该最后的长度,那么说明这个字符串就是我们需要的;
②紧接着进行遍历操作,查找还未使用的序列,并尝试使用该字母:
- 如果该怎么标记为0 ,则表示没有使用过,如果没有使用过则把它加入到 【tmp】里面,紧接着标记为1,表示已经使用过该字母;
- 然后从当前位置的下一个位置开始在进行遍历操作;
- 等到它从下一个位置遍历后来之后,我们就需要弹出【tmp】中的元素,并把它标记为0在进行下一步遍历
③如果我们已经使用了【i】位置处的值,那么后面与它相等的就不在使用,直接进行 ++操作
💨 结果展示:
还有两道题,一道是去重的,另外一道是不去重的,大家可以自己尝试做做看,如果以下两题自己会做了,那么对于全排列算法,大家基本上就掌握了。
链接如下:全排列
链接如下:全排列 ||
(五)总结
到此,关于全排列算法就讲到这里了。希望本文对大家有所帮助,感谢各位的观看!!