八皇后
在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?
源码
public class Demo {
static int TRUE = 1, FALSE = 0, EIGHT = 8;
static int[] queen = new int[EIGHT];
static int number = 0;
static int count=0;
//构造函数
public Demo() {
number = 0;
}
public static void print1(){
count++;
for(int i=0;i<EIGHT;i++){
System.out.print(queen[i]+" ");
}
System.out.println();
}
//判断在(row,col)上的皇后是否遭受攻击
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
//确定皇后放的位置
public static void thePlace(int row){
if(row==EIGHT){
print1();
print2();
return;
}
for(int i=0;i<EIGHT;i++){
queen[row]=i;
if(attack(row))
thePlace(row+1);
}
}
public static void main(String[] args){
thePlace(0);
System.out.println(count);
}
}
图示分析秒懂源码
static int[] queen = new int[EIGHT];
注释:源码中row代表行数,请读者想象出一个棋盘,这里定义一个一维数组queen[EIGHT];用一维数组的每一个源数的下标作为行号,下标对应的数组中的数值作为列号。所以每打印出来的一个一维数中的每一个元素及其对应的下标即为每一种情况下对应的所有落子的坐标
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
attack()方法是用来判断,其落子处所对应的列号和对角线上是否有其他皇后,如果有则不进入递归,反之则进入递归,
解析:
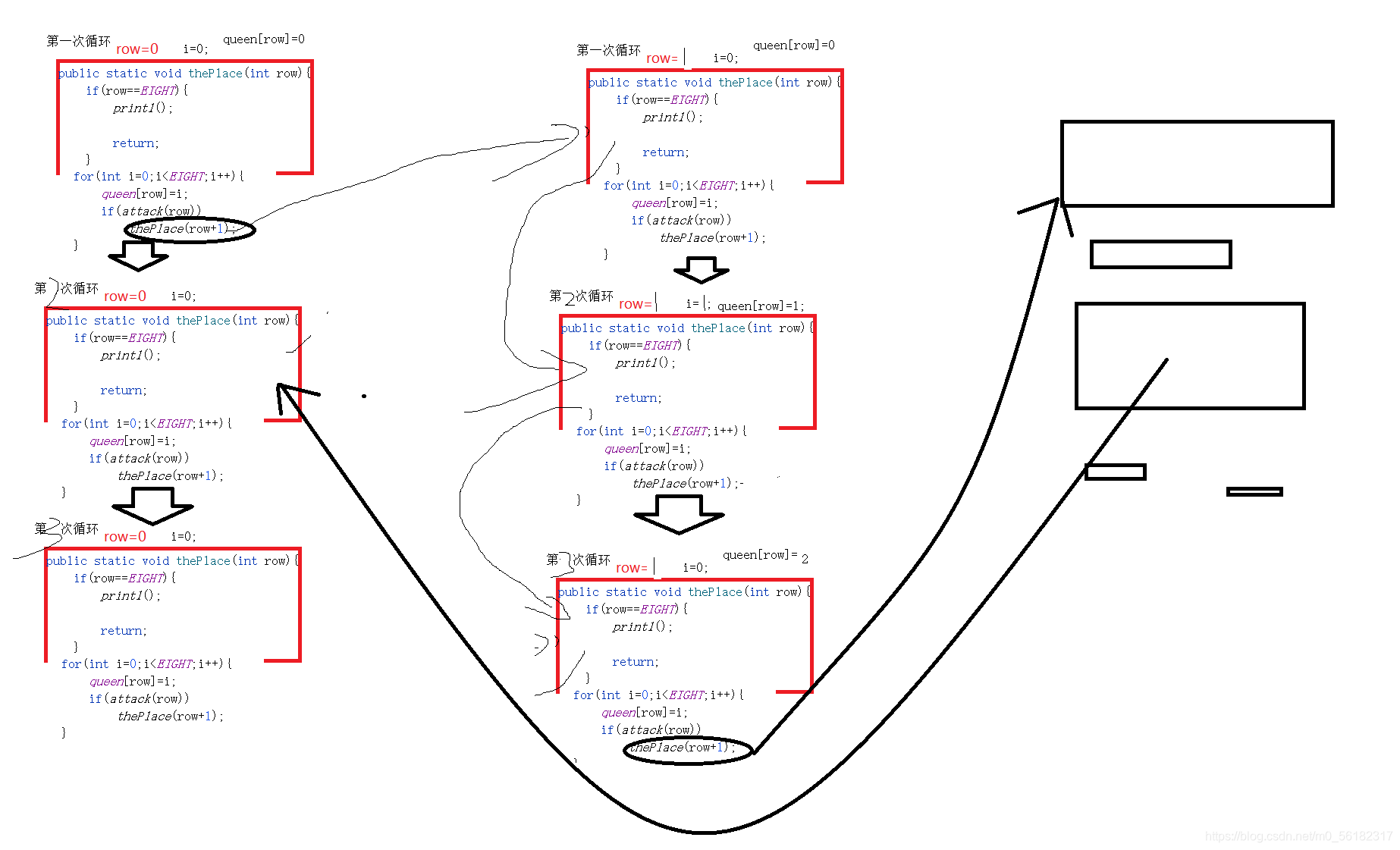
注意看源码中,main函数在最底下,仅调用了 thePlace()方法,传入参数为0,即在此方法中row(行数)先为0,先判断row(行数)是否等于EIGHT(EIGHT=8);不等于,往下进入for循环,for循环中有涉及递归,注意看下面的图示:
第一次棋盘为空直接落子,进入递归。
每一次进入递归都是因为找到了确定的行中的某一列可以落子的地方。找不到则在当前递归层数中进入for循环,直到找到可以落子的地方。如果循环到头,则返回上一层递归中的for循环。如此一直循环下去则可以统计出所有情况。
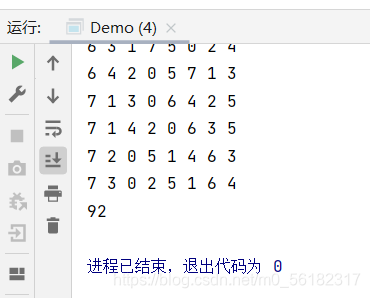
再进阶:把每一种情况的棋图都打印出来
public static void print2(){
String[][] arr={{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "}};
for(int i=0;i<EIGHT;i++){
arr[i][queen[i]]="*";
}
for(int i=0;i<EIGHT;i++){
for(int j=0;j<EIGHT;j++) {
if(j<EIGHT-1) {
System.out.print(" " + arr[i][j] + " ");
System.out.print("|");
}else{
System.out.print(" " + arr[i][j] + " ");
}
}
System.out.println();
if(i<EIGHT-1){
for (int k = 0; k < EIGHT; k++) {
if(k==7)
System.out.print("---");
else
System.out.print("---|");
}
}
System.out.println();
}
}
整体代码实现
package 八皇后问题;
public class Demo {
static int TRUE = 1, FALSE = 0, EIGHT = 8;
static int[] queen = new int[EIGHT];
static int number = 0;
static int count=0;
//构造函数
public Demo() {
number = 0;
}
//打印一维数组结果
public static void print1(){
count++;
for(int i=0;i<EIGHT;i++){
System.out.print(queen[i]+" ");
}
System.out.println();
}
//打印棋盘式结果
public static void print2(){
String[][] arr={{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "}};
for(int i=0;i<EIGHT;i++){
arr[i][queen[i]]="*";
}
for(int i=0;i<EIGHT;i++){
for(int j=0;j<EIGHT;j++) {
if(j<EIGHT-1) {
System.out.print(" " + arr[i][j] + " ");
System.out.print("|");
}else{
System.out.print(" " + arr[i][j] + " ");
}
}
System.out.println();
if(i<EIGHT-1){
for (int k = 0; k < EIGHT; k++) {
if(k==7)
System.out.print("---");
else
System.out.print("---|");
}
}
System.out.println();
}
}
//判断在(row,col)上的皇后是否遭受攻击
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
//确定皇后放的位置
public static void thePlace(int row){
if(row==EIGHT){
print1();
print2();
return;
}
for(int i=0;i<EIGHT;i++){
queen[row]=i;
if(attack(row))
thePlace(row+1);
}
}
public static void main(String[] args){
thePlace(0);
System.out.println(count);
}
}
汉诺塔
汉诺塔:汉诺塔(Tower of Hanoi)源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
当圆盘为n时,一共要挪动多少次?
源码
import java.util.Scanner;
public class Demo2 {
static int times;
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
System.out.println("请输入盘子数量");
int j=sc.nextInt();
hanoi(j,'A','B','C');
}
public static void move(int disk,char p1,char p3){
System.out.println("第"+(++Demo2.times)+"次将"+disk+"从"+p1+"移动到"+p3);
}
public static void hanoi(int n,char p1,char p2,char p3){
if(n==1) {
move(n,p1, p3);
}else{
//将n-1个圆盘移到B柱上
hanoi(n-1,p1,p3,p2);
//将最后一个圆盘移到C柱上
move(n,p1,p3);
//将n-1个圆盘移到C柱上
hanoi(n-1,p2,p1,p3);
}
}
}
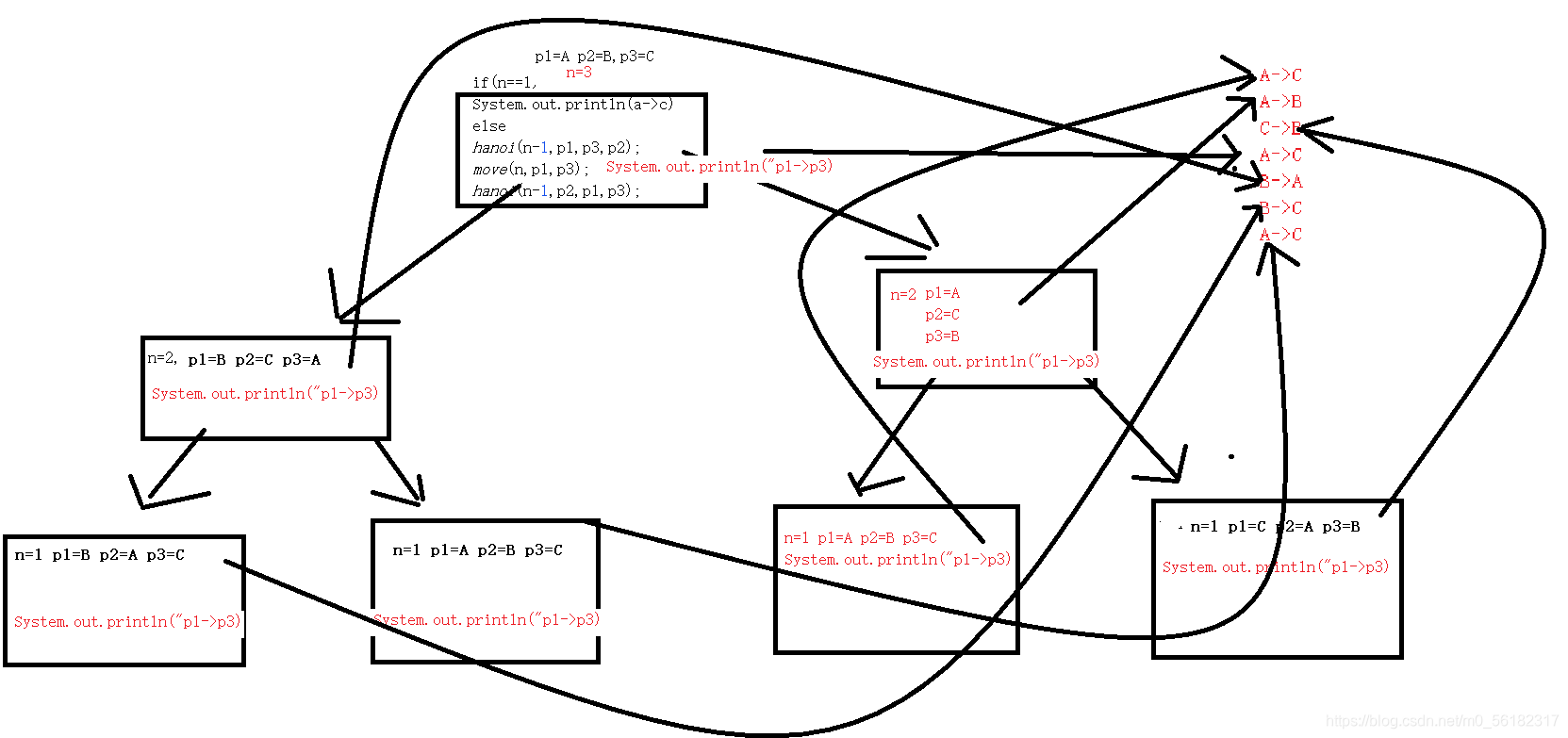
图示分析秒杀源码
以n=3进行分析。
迷宫问题之在源码解释
有一个迷宫地图,有一些可达的位置,也有一些不可达的位置(障碍、墙壁、边界)。从一个位置到下一个位置只能通过向上(或者向右、或者向下、或者向左)走一步来实现,从起点出发,如何找到一条到达终点的通路。并在走过的路径下留下标记。
先用链表模拟一个堆栈:
public class Node {
int x;
int y;
Node next;
public Node(){}
public Node(int x,int y){
this.x =x;
this.y =y;
next=null;
}
}
public class NodeList {
Node first;
Node last;
//压栈
public void push(int x,int y){
Node newNode=new Node(x,y);
if(first==null){
first=newNode;
last=newNode;
}else{
last.next=newNode;
last=newNode;
}
}
//出栈
public void pop(){
if(first==null){
System.out.println("堆栈已满,误删除选项");
return;
}else{
Node delNode=first;
while(delNode.next!=last)
delNode=delNode.next;
delNode.next=last.next;
last=delNode;
}
}
}
操作堆栈解决问题
public class Demo {
public static int exitx=8;
public static int exity=10;
public static int[][] arr = {{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
};
public static void main(String[] args) {
int x = 1;
int y = 1;
NodeList L = new NodeList();
System.out.println("老鼠走前");
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 12; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
while (x <=exitx&&y<=exity){
arr[x][y]=2;
if(arr[x-1][y]==0){
x--;
L.push(x,y);
}else if(arr[x+1][y]==0){
x++;
L.push(x,y);
}else if(arr[x][y-1]==0){
y--;
L.push(x,y);
}else if(arr[x][y+1]==0){
y++;
L.push(x,y);
}else{
if(chkExit(x,y,exitx,exity)){
break;
}
else{
arr[x][y]=2;
L.pop();
x=L.last.x;
y=L.last.y;
}
}
}
System.out.println("老鼠走后");
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 12; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
public static boolean chkExit(int x,int y,int exitx,int exity) {
if (x == exitx && y == exity) {
if(arr[x-1][y]==1||arr[x+1][y]==1||arr[x][y-1]==1||arr[x][y+1]==2){
return true;
}else if(arr[x-1][y]==1||arr[x+1][y]==1||arr[x][y-1]==2||arr[x][y+1]==1){
return true;
}else if(arr[x-1][y]==1||arr[x+1][y]==2||arr[x][y-1]==1||arr[x][y+1]==1){
return true;
}else if(arr[x-1][y]==2||arr[x+1][y]==1||arr[x][y-1]==1||arr[x][y+1]==1)
return true;
else
return false;
}else{
return false;
}
}
}