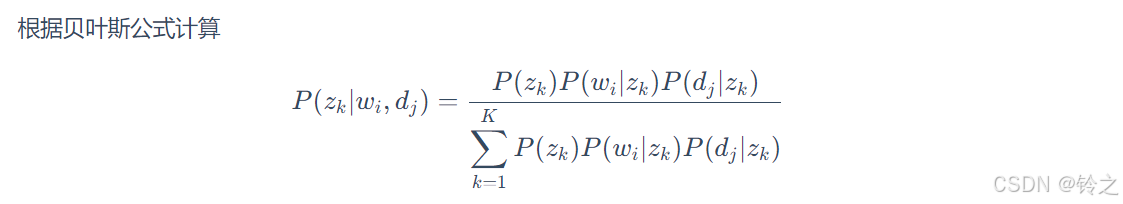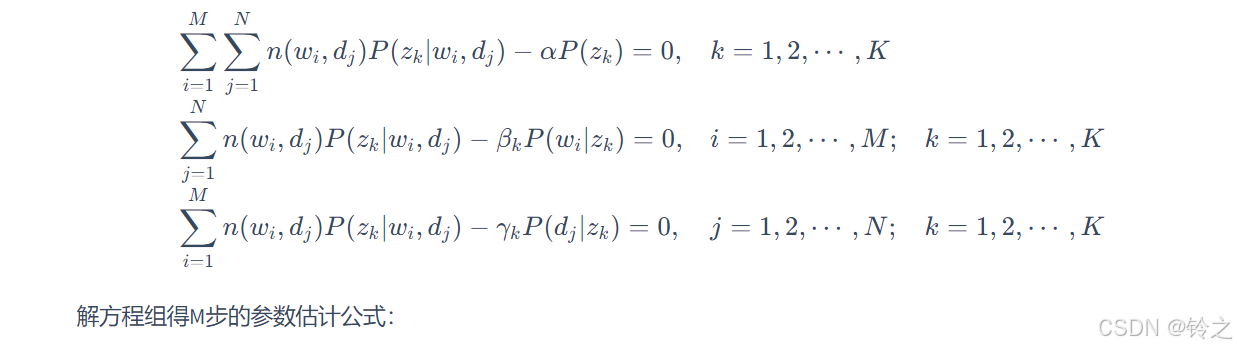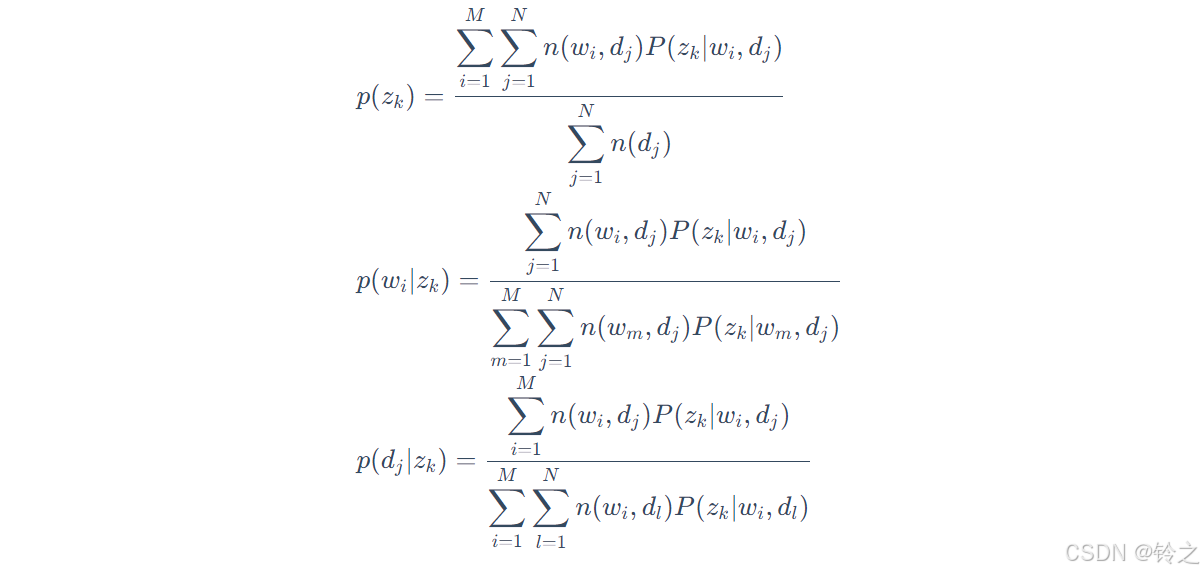本章概要:
1.概率潜在语义分析是利用概率生成模型对文本集合进行话题分析的方法。概率潜在语义分析受潜在语义分析的启发提出两者可以通过矩阵分解关联起来。
给定一个文本集合,通过概率潜在语义分析,可以得到各个文本生成话题的条件概率分布,以及各个话题生成单词的条件概率分布。
概率潜在语义分析的模型有生成模型,以及等价的共现模型。其学习策略是观测数据的极大似然估计,其学习算法是EM算法。
2.生成模型表示文本生成话题,话题生成单词从而得到单词文本共现数据的过程;假设每个文本由一个话题分布决定,每个话题由一个单词分布决定。单词变量 w w w与文本变量 d d d是观测变量话题变量 z z z是隐变量。
生成模型通过以下过程生成文档:
- 选择一个文档 d d d。
- 从文档 d d d 的主题分布 P ( z ∣ d ) P(z|d) P(z∣d) 中选择一个主题 z z z。
- 从主题 z z z 的词语分布 P ( w ∣ z ) P(w|z) P(w∣z) 中选择一个词语 w w w。
生成模型的定义如下:
P
(
T
)
=
∏
(
w
,
d
)
P
(
w
,
d
)
n
(
w
,
d
)
P ( T ) = \prod _ { ( w , d ) } P ( w , d ) ^ { n ( w , d ) }
P(T)=(w,d)∏P(w,d)n(w,d)
P
(
w
,
d
)
=
P
(
d
)
P
(
w
∣
d
)
=
P
(
d
)
∑
z
P
(
z
∣
d
)
P
(
w
∣
z
)
P ( w , d ) = P ( d ) P ( w | d ) = P ( d ) \sum _z P ( z | d ) P ( w | z )
P(w,d)=P(d)P(w∣d)=P(d)z∑P(z∣d)P(w∣z)
3.共现模型描述文本单词共现数据拥有的模式。共现模型的定义如下:
P
(
T
)
=
∏
(
w
,
d
)
P
(
w
,
d
)
n
(
w
,
d
)
P ( T ) = \prod _ { ( w , d ) } P ( w , d ) ^ { n ( w , d ) }
P(T)=(w,d)∏P(w,d)n(w,d)
P ( w , d ) = ∑ z ∈ Z P ( z ) P ( w ∣ z ) P ( d ∣ z ) P ( w , d ) = \sum _ { z \in Z } P ( z ) P ( w | z ) P ( d | z ) P(w,d)=z∈Z∑P(z)P(w∣z)P(d∣z)
4.概率潜在语义分析的模型的参数个数是 O ( M ⋅ K + N ⋅ K ) O ( M \cdot K + N \cdot K ) O(M⋅K+N⋅K)。现实中 K ≪ M K \ll M K≪M,所以概率潜在语义分析通过话题对数据进行了更简洁地表示,实现了数据压缩。
5.模型中的概率分布 P ( w ∣ d ) P ( w | d ) P(w∣d)可以由参数空间中的单纯形表示。 M M M维参数空间中,单词单纯形表示所有可能的文本的分布,其中的话题单纯形表示在 K K K个话题定义下的所有可能的文本的分布。话题单纯形是单词单纯形的子集,表示潜在语义空间。
6.概率潜在语义分析的学习通常采用EM算法通过迭代学习模型的参数,
P
(
w
∣
z
)
P ( w | z )
P(w∣z)
和
P
(
z
∣
d
)
P ( z| d )
P(z∣d),而
P
(
d
)
P(d)
P(d)可直接统计得出。
概率潜在语义模型(生成模型)参数估计的EM算法:
输入: 设单词集合为 W = { w 1 , w 2 , . . . , w M } W = \{w_{1}, w_{2},..., w_{M}\} W={w1,w2,...,wM}, 文本集合为 D = { d 1 , d 2 , . . . , d N } D=\{d_{1}, d_{2},..., d_{N}\} D={d1,d2,...,dN}, 话题集合为 Z = { z 1 , z 2 , . . . , z K } Z=\{z_{1}, z_{2},..., z_{K}\} Z={z1,z2,...,zK}, 共现数据 { n ( w i , d j ) } , i = 1 , 2 , . . . , M , j = 1 , 2 , . . . , N ; \left \{ n(w_{i}, d_{j}) \right \}, i = 1,2,..., M, j = 1,2,...,N; {n(wi,dj)},i=1,2,...,M,j=1,2,...,N;
输出: P ( w i ∣ z k ) P(w_{i}|z_{k}) P(wi∣zk) 和 P ( z k ∣ d j ) P(z_{k}|d_{j}) P(zk∣dj).
-
设置参数 P ( w i ∣ z k ) P(w_{i}|z_{k}) P(wi∣zk) 和 P ( z k ∣ d j ) P(z_{k}|d_{j}) P(zk∣dj) 的初始值。
-
迭代执行以下E步,M步,直到收敛为止。
E步:
P
(
z
k
∣
w
i
,
d
j
)
=
P
(
w
i
∣
z
k
)
P
(
z
k
∣
d
j
)
∑
k
=
1
K
P
(
w
i
∣
z
k
)
P
(
z
k
∣
d
j
)
P(z_{k}|w_{i},d_{j})=\frac{P(w_{i}|z_{k})P(z_{k}|d_{j})}{\sum_{k=1}^{K}P(w_{i}|z_{k})P(z_{k}|d_{j})}
P(zk∣wi,dj)=∑k=1KP(wi∣zk)P(zk∣dj)P(wi∣zk)P(zk∣dj)
M步:
P
(
w
i
∣
z
k
)
=
∑
j
=
1
N
n
(
w
i
,
d
j
)
P
(
z
k
∣
w
i
,
d
j
)
∑
m
=
1
M
∑
j
=
1
N
n
(
w
m
,
d
j
)
P
(
z
k
∣
w
m
,
d
j
)
P(w_{i}|z_{k})=\frac{\sum_{j=1}^{N}n(w_{i},d_{j})P(z_{k}|w_{i},d_{j})}{\sum_{m=1}^{M}\sum_{j=1}^{N}n(w_{m},d_{j})P(z_{k}|w_{m},d_{j})}
P(wi∣zk)=∑m=1M∑j=1Nn(wm,dj)P(zk∣wm,dj)∑j=1Nn(wi,dj)P(zk∣wi,dj)
P ( z k ∣ d j ) = ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) n ( d j ) P(z_{k}|d_{j}) = \frac{\sum_{i=1}^{M}n(w_{i},d_{j})P(z_{k}|w_{i},d_{j})}{n(d_{j})} P(zk∣dj)=n(dj)∑i=1Mn(wi,dj)P(zk∣wi,dj)
其他公式见文章:潜在语义分析 (LSA),概率潜在语义分析 (PLSA)
习题18.1
证明生成模型与共现模型是等价的。
P ( w , d ) = P ( d ) ∑ z P ( z ∣ d ) P ( w ∣ z ) = ∑ z P ( w ∣ z ) P ( z ∣ d ) P ( d ) = ∑ z P ( w , z ∣ d ) P ( d ) = ∑ z P ( w , d , z ) = ∑ z P ( z ) P ( w , d ∣ z ) = ∑ z P ( z ) P ( w ∣ z ) P ( d ∣ z ) \begin{aligned} P(w,d) &= P(d) \sum_z P(z|d)P(w|z) \\ &= \sum_z P(w|z)P(z|d)P(d) \\ &= \sum_z P(w,z|d)P(d) \\ &= \sum_z P(w,d,z) \\ &= \sum_z P(z)P(w,d|z) \\ &= \sum_z P(z)P(w|z)P(d|z) \end{aligned} P(w,d)=P(d)z∑P(z∣d)P(w∣z)=z∑P(w∣z)P(z∣d)P(d)=z∑P(w,z∣d)P(d)=z∑P(w,d,z)=z∑P(z)P(w,d∣z)=z∑P(z)P(w∣z)P(d∣z)
习题18.2
推导共现模型的EM算法。
解答:
推导过程与生成模型的EM算法是一致的,非常容易。
习题18.3
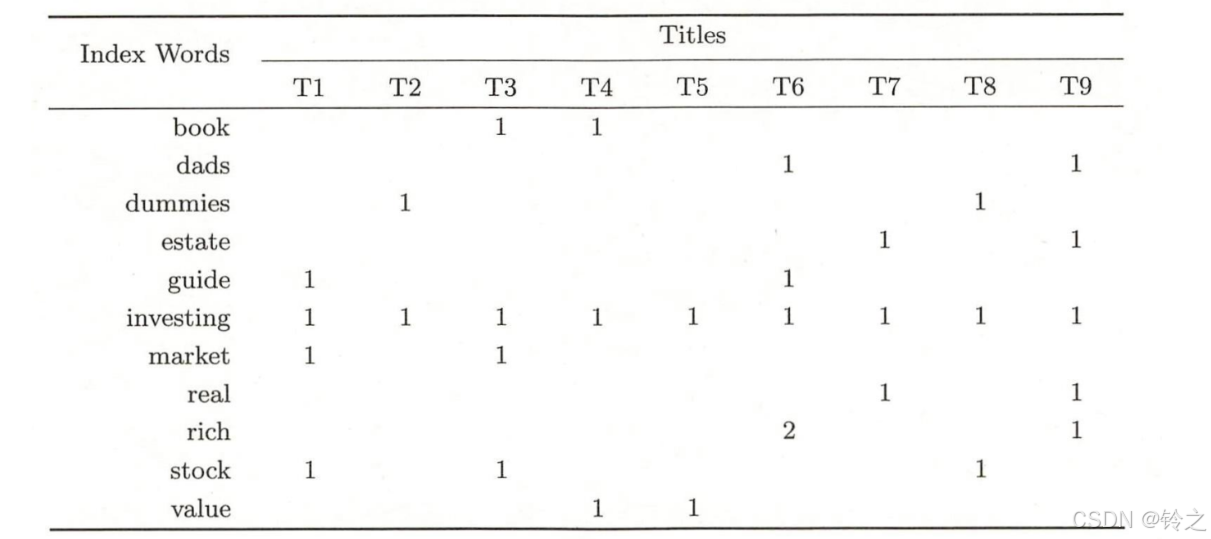
对以下文本数据集进行概率潜在语义分析。
import numpy as np
class EMPlsa:
def __init__(self, max_iter=100, tol=1e-4, random_state=2022):
"""
基于生成模型的EM算法的概率潜在语义模型
:param max_iter: 最大迭代次数
:param tol: 收敛阈值
:param random_state: 随机种子
"""
self.max_iter = max_iter
self.tol = tol
self.random_state = random_state
def fit(self, X, K):
"""
:param X: 单词-文本矩阵
:param K: 话题个数
:return: P(w_i|z_k) 和 P(z_k|d_j)
"""
# M, N分别为单词个数和文本个数
M, N = X.shape
# 计算n(d_j)
n_d = np.sum(X, axis=0)
# (1)设置参数P(w_i|z_k)和P(z_k|d_j)的初始值
np.random.seed(self.random_state)
p_wz = np.random.random((M, K))
p_zd = np.random.random((K, N))
# 归一化初始值
p_wz /= np.sum(p_wz, axis=0)
p_zd /= np.sum(p_zd, axis=0)
prev_likelihood = None
# (2)迭代执行E步和M步,直至收敛为止
for iteration in range(self.max_iter):
# E步
P = np.einsum('ik,kj->ijk', p_wz, p_zd) # 对于每一个词 i 和每一个文档 j,计算所有主题 k 的组合。具体来说,每个 P[i][j][k] 是 p_wz[i][k] * p_zd[k][j] 的结果。
P /= np.sum(P, axis=2, keepdims=True) # 归一化操作,使得每个词和文档在所有主题上的概率分布之和为 1
# M步
p_wz = np.einsum('ij,ijk->ik', X, P)
p_wz /= np.sum(p_wz, axis=0, keepdims=True)
p_zd = np.einsum('ij,ijk->kj', X, P)
p_zd /= np.sum(p_zd, axis=1, keepdims=True)
# 计算对数似然
likelihood = np.sum(X * np.log(np.einsum('ik,kj->ij', p_wz, p_zd)))
if prev_likelihood is not None and abs(likelihood - prev_likelihood) < self.tol:
break
prev_likelihood = likelihood
return p_wz, p_zd
# 输入文本-单词矩阵,共有9个文本,11个单词
X = np.array([[0, 0, 1, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 1],
[0, 1, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 0, 2, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 1, 1, 0, 0, 0, 0]])
# 设置精度为3
np.set_printoptions(precision=3, suppress=True)
# 假设话题的个数是3个
k = 3
em_plsa = EMPlsa(max_iter=1000)
p_wz, p_zd = em_plsa.fit(X, 3)
print("参数P(w_i|z_k):")
print(p_wz)
print("参数P(z_k|d_j):")
print(p_zd)
参数P(w_i|z_k):
[[0. 0.188 0. ]
[0. 0. 0.2 ]
[0.192 0. 0. ]
[0.096 0. 0.1 ]
[0. 0.094 0.1 ]
[0.423 0.246 0.2 ]
[0. 0.188 0. ]
[0.096 0. 0.1 ]
[0. 0. 0.3 ]
[0. 0.283 0. ]
[0.192 0. 0. ]]
参数P(z_k|d_j):
[[0. 0.192 0. 0.163 0.192 0. 0.289 0.163 0. ]
[0.377 0. 0.377 0.123 0. 0. 0. 0.123 0. ]
[0. 0. 0. 0. 0. 0.5 0. 0. 0.5 ]]
使用书籍:李航《机器学习方法》
习题解答:https://datawhalechina.github.io/statistical-learning-method-solutions-manual/#/chapter18/ch18