Bootstrap

【数据结构初阶】栈和队列（C语言实现+图解）

文章目录

栈

栈的概念及结构

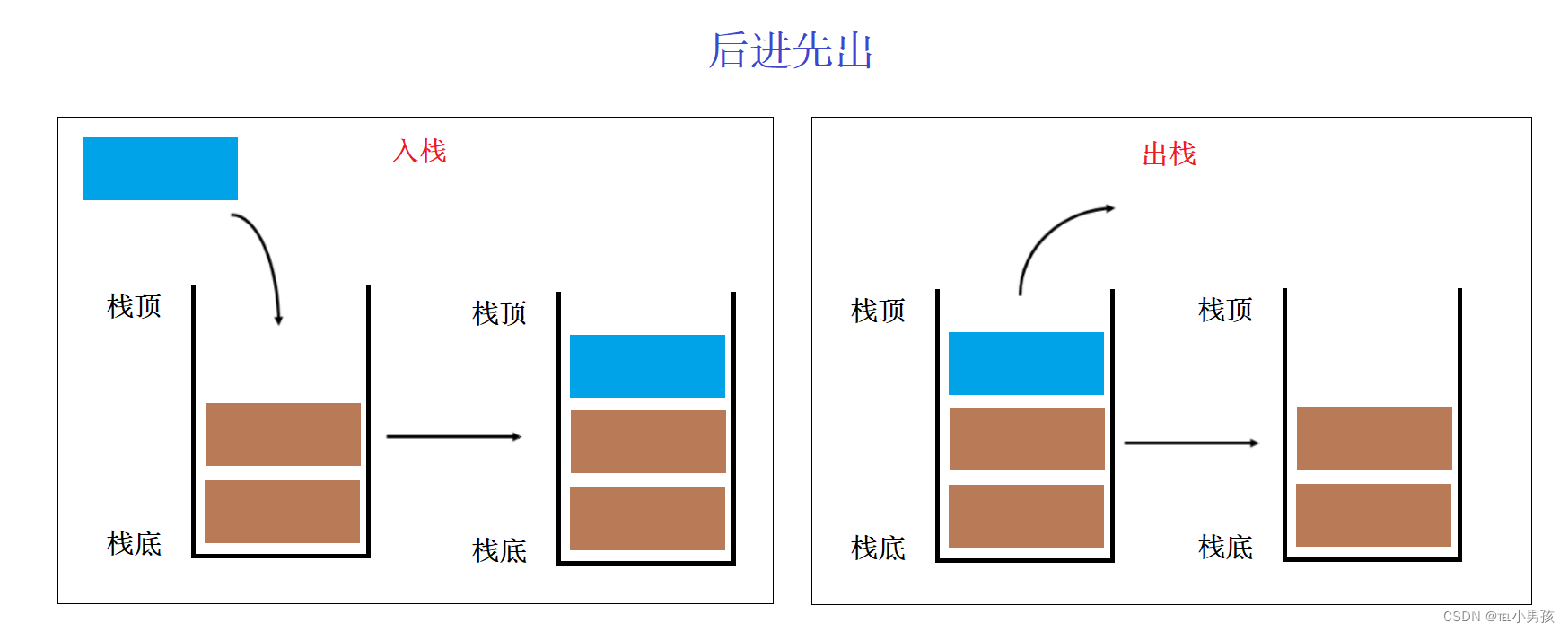
栈：是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

压栈： 从栈顶放入数据的操作被称为压栈，也可以叫做进栈、入栈。

出栈： 删除栈顶数据的操作被称为出栈，也可以叫做弹栈。
在这里插入图片描述

栈的实现

栈的实现一般可以使用数组或者链表实现。那如何选择呢？我们来分析一下。

链表栈： 如果选择单链表的话，我们因该选头结点当栈顶，尾结点当栈底，否则，每次存取数据的时候都必须遍历链表，其次，需要频繁的申请结点，对内存会有一定损耗。所以如果选链表栈的话，推荐选择双向链表会比较好点。

数组栈： 对于数组栈来说，访问栈顶的时间复杂度为O(1)，虽动态增容时会有一定的消耗，在增容次数不会很多。所以相比链表栈，数组栈更优。
所以下面我们用顺序表来实现栈

栈结构体定义

结构如下

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;//指向为栈开辟的空间
	int top;//指向栈顶，相当于顺序表中的size
	int capacity;//容量
}ST;
栈的接口

栈实现的接口主要有以下几个：

//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//取栈顶元素
STDataType StackTop(ST* ps);
//判空
bool StackEmpty(ST* ps);
//计算栈中元素个数
int StackSize(ST* ps);
栈的初始化

代码实现：

//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

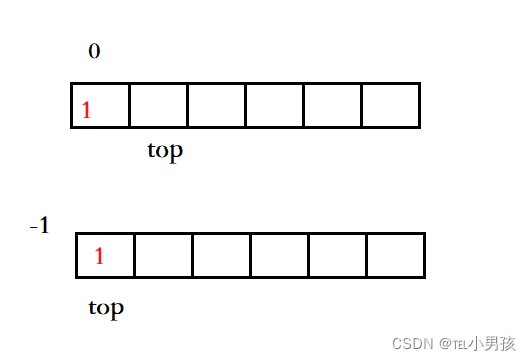
注意：top可以初始化为0，也可以初始化为-1

  • 若为0，则top为栈顶元素的下一个位置，其值代表元素个数
  • 若为-1，则top为当前栈顶元素的下标，其值+1才代表元素个数

在这里插入图片描述

栈的销毁

为了防止内存泄露，动态内存申请的空间一定要我们自己手动释放，养成一个良好的习惯。

//销毁
//销毁
void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}
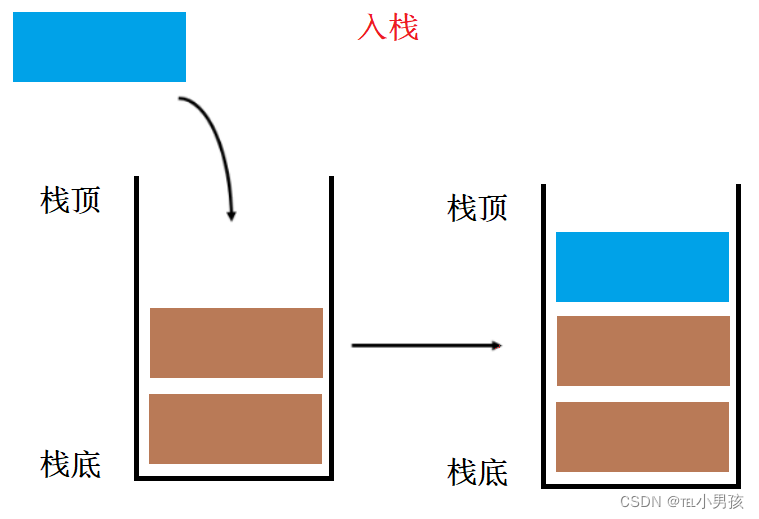
入栈

入栈就是在栈顶插入数据，在插入数据之前，我们需要考虑扩容的问题，当ps->top == ps->capacity的时候，就需要扩容了，扩容和顺序表一样每次扩一倍，这样可以减少扩容的次数，但同时可能会带来一定的空间浪费。
在这里插入图片描述
代码实现

//入栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	//需要判断栈是否满了,满了就要扩容
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;

		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
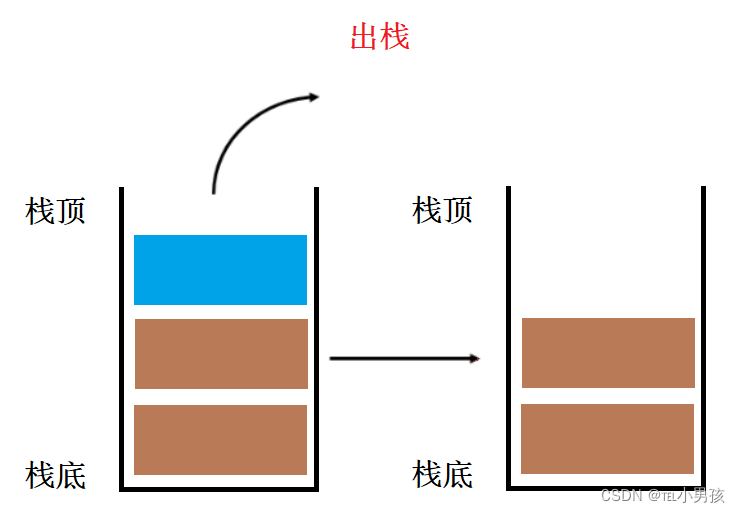
出栈

出栈就是删除栈顶的元素，也就是top-1指向的位置，所以我们只需将top减一操作即可。
我们在出栈的过程中还需注意一点，就是栈是否为空，如果为空，就不能进行操作
在这里插入图片描述

代码实现：

//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	ps->top--;
}
取栈顶元素

因为栈顶元素的下标是top-1，所以我们只需返回top-1位置的元素即可。同时我们也需要注意栈是否为空

代码实现：

//取栈顶元素
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	return ps->a[ps->top - 1];
}
判断栈是否为空

因为我们的top是初始化为0，其值代表栈中元素的个数，所以，当top == 0就代表栈空。

代码实现：

//判空
bool StackEmpty(ST* ps)
{
	assert(ps);

	return ps->top == 0;
}
栈的元素个数

top就是栈中元素的个数，返回top即可

代码实现：


//计算栈中元素个数
int StackSize(ST* ps)
{
	assert(ps);

	return ps->top;
}

完整代码

//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

//销毁
void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

//入栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	//需要判断栈是否满了,满了就要扩容
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;

		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}

//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	ps->top--;
}

//取栈顶元素
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	return ps->a[ps->top - 1];
}

//判空
bool StackEmpty(ST* ps)
{
	assert(ps);

	return ps->top == 0;
}

//计算栈中元素个数
int StackSize(ST* ps)
{
	assert(ps);

	return ps->top;
}

队列

队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)的原则
请添加图片描述
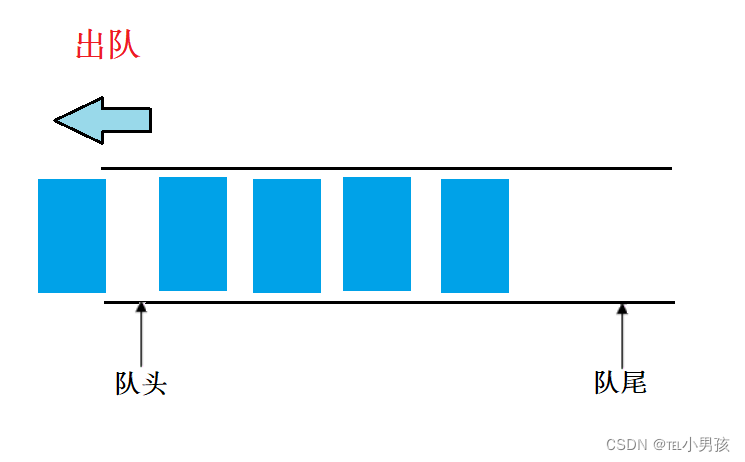
队头： 进行删除操作的一端称为队头

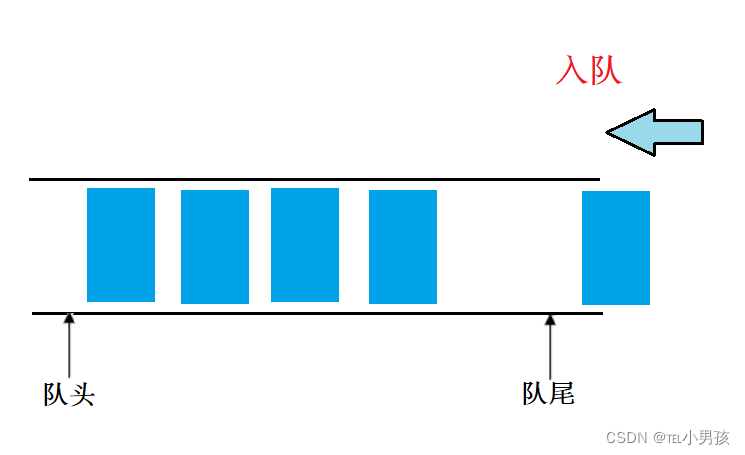
队尾： 进行插入操作的一端称为队尾

入队列即在队尾插入数据，出队列则是在队头删除数据。

队列的实现

队列也可以使用数组和链表来实现，我们选择使用单链表来实现，只需进行头删和尾插，如果使用数组的话，那么每一次删头，我们都需要挪动数据，效率不高。

队列结构体定义

定义结构如下：

typedef int QDataType;
//结点
typedef struct QueueNode
{
	struct Queue* next;
	QDataType data;
}QNode;
//队列
typedef struct Queue
{
	QNode* head;//记录链表的头
	QNode* tail;//记录链表的尾
	int size;//记录队列的元素个数
}Queue;

队列需要两个指针标识队头和队尾，以便管理队列的元素。而队列元素即结点用单链表的结构实现即可。把结点封装成一个结构体，队列再封装成一个结构体存入指向结点结构体的指针。

如果不定义Queue结构体或者是说不将 头尾指针 封装起来的也是可以的，不过这样我们在传参时就需要使用二级指针了。

void QueueInit(QNode** pphead, QNode* pptail);
队列的接口

队列实现的接口主要有以下几个：

//初始化
void QueueInit(Queue* pq);
//销毁
void QueueDestroy(Queue* pq);
//入队
void QueuePush(Queue* pq, QDataType x);
//出队
void QueuePop(Queue* pq);

//取队头元素
QDataType QueueFront(Queue* pq);
//取队尾元素
QDataType QueueBack(Queue* pq);

//判空
bool QueueEmpty(Queue* pq);

//计算队列大小
int QueueSize(Queue* pq);
队列的初始化

代码实现：

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
队列的销毁

代码实现：

//销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;

	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
}

初始化和销毁并没有传二级指针，因为传递的是队列结构体的地址，而两个头尾指针是封装在队列结构体里的。创建队列在函数外，所以传其地址就行，同时加上断言以防空指针。

入队

入队其实就是单链表尾插的操作，进行尾插需要判断链表为不为空。
为空时需要改变头尾指针的指向，不为空就不需要了。
在这里插入图片描述

代码实现：

//入队
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	//首先需要申请一个新结点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->next = NULL;
	}

	//队列为空
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	//队列不为空
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

	pq->size++;
}
出队

出队其实就是单链表头删的操作，进行头删时，需要注意链表是否为空，还需要考虑当链表只有一个结点的情况

在这里插入图片描述

代码实现：

//出队
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));//判断链表是否为空

	//只有一个元素
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail =  NULL;
	}
	//多个元素
	else
	{
		QNode* del = pq->head;
		pq->head = pq->head->next;
		free(del);
		del = NULL;
	}
	pq->size--;
}
取队头和队尾元素

取队头元素就是返回头结点的数据，取队尾元素就是返回尾结点的数据

代码实现：

//取队头元素
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}
//取队尾元素
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}
判断队列是否为空

当pq->head==NULL且pq->tail==NULL则链表为空

代码实现：

//判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->head == NULL && pq->tail == NULL;
}
统计队列元素个数

队列结构体中的size就是统计队列元素的个数

代码实现：

//计算队列中元素的个数
int QueueSize(Queue* pq)
{
	assert(pq);

	return pq->size;
}

完整代码

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
//销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;

	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
}
//入队
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	//首先需要申请一个新结点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->next = NULL;
	}

	//队列为空
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	//队列不为空
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

	pq->size++;
}
//出队
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	//只有一个元素
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail =  NULL;
	}
	//多个元素
	else
	{
		QNode* del = pq->head;
		pq->head = pq->head->next;
		free(del);
		del = NULL;
	}
	pq->size--;
}

//取队头元素
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}
//取队尾元素
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

//判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->head == NULL && pq->tail == NULL;
}

//计算队列大小
int QueueSize(Queue* pq)
{
	assert(pq);

	return pq->size;
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
SAP从放弃到入门系列之-5种库存转储测试
vue如何使用rules对表单字段进行校验
Unity制作一个小地图
LeetCode 1943. 描述绘画结果
AI革命之芯：如何Transformer正在重塑我们的世界观！
Clion 中无法用相对路径读入文件
红队常用攻击套路
计算机毕业设计项目：基于ssm的大学校园慈善拍卖网站的设计 80891（开题答辩+程序定制+全套文案 ）上万套实战教程手把手教学JAVA、PHP，node.js，C++、python等
Redis6
树莓派部署django，并利用ngrok配置公网域名
;