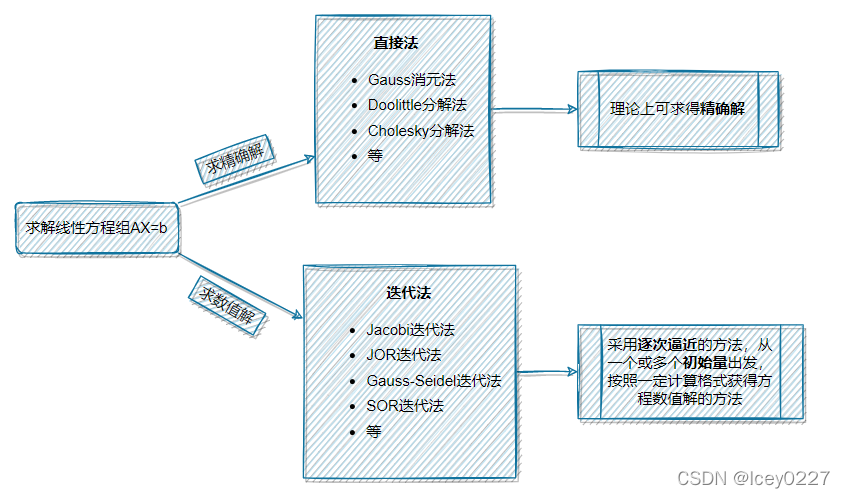
线性方程组的数值解法

在科学工程计算中，我们常通过直接法和迭代法求解线性方程组:$$AX=b$$其中 $A\in R^{n\times n}$为非奇异矩阵，且
$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \dots & a_{nn}\end{array}\right),X=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right),b=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right)$$

直接法

高斯消元法

顺序消元法

为了更加直观的体现消元过程，我们举一个三维矩阵的例子：
$$\begin{gathered} \left(\begin{array}{ccc}3& 2& 1\\ 2& 1& 4\\ 1& 3& 6\end{array}\right)\left(\begin{array}{c}{m}_1\\ m_2\\ m_3\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right) \\ 对应增广矩阵：\left(\begin{array}{cccc}3& 2& 1|& m_1\\ 2& 1& 4|& m_2\\ 1& 3& 6|& m_3\end{array}\right) \\ 接下来主要针对系数矩阵对应的子矩阵来体现顺序消元的过程： \\ \left(\begin{array}{cccc}3& 2& 1|& m_1\\ 2& 1& 4|& m_2\\ 1& 3& 6|& m_3\end{array}\right)\Rightarrow \left(\begin{array}{cccc}3& 2& 1& |m_{11}\\ 2+3\times (-\frac{2}{3})& 1+2\times (-\frac{2}{3})& 4+1\times (-\frac{2}{3})& |m_{21}\\ 1+3\times (-\frac{1}{3})& 3+2\times (-\frac{1}{3})& 6+1\times (-\frac{1}{3})& |m_{31}\end{array}\right) \\ =\left(\begin{array}{cccc}3& 2& 1& |m_{11}\\ 0& -\frac{1}{3}& \frac{10}{3}& |m_{21}\\ 0& \frac{7}{3}& \frac{17}{3}& |m_{31}\end{array}\right) \\ \Rightarrow \left(\begin{array}{cccc}3& 2& 1& |m_{12}\\ 0& -\frac{1}{3}& \frac{10}{3}& |m_{22}\\ 0& \frac{7}{3}+(-\frac{1}{3})\times 7& \frac{17}{3}+\frac{10}{3}\times 7)& |m_{32}\end{array}\right) \\ =\left(\begin{array}{cccc}3& 2& 1& |m_{12}\\ 0& -\frac{1}{3}& \frac{10}{3}& |m_{22}\\ 0& 0& 29& |m_{32}\end{array}\right) \end{gathered}$$
“前推”（方法核心）至此结束，之后进行“回代”即可得到线性方程组的解$X={\left(\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right)}^T$
由此思路可以推广到到$n$维的一般情况。

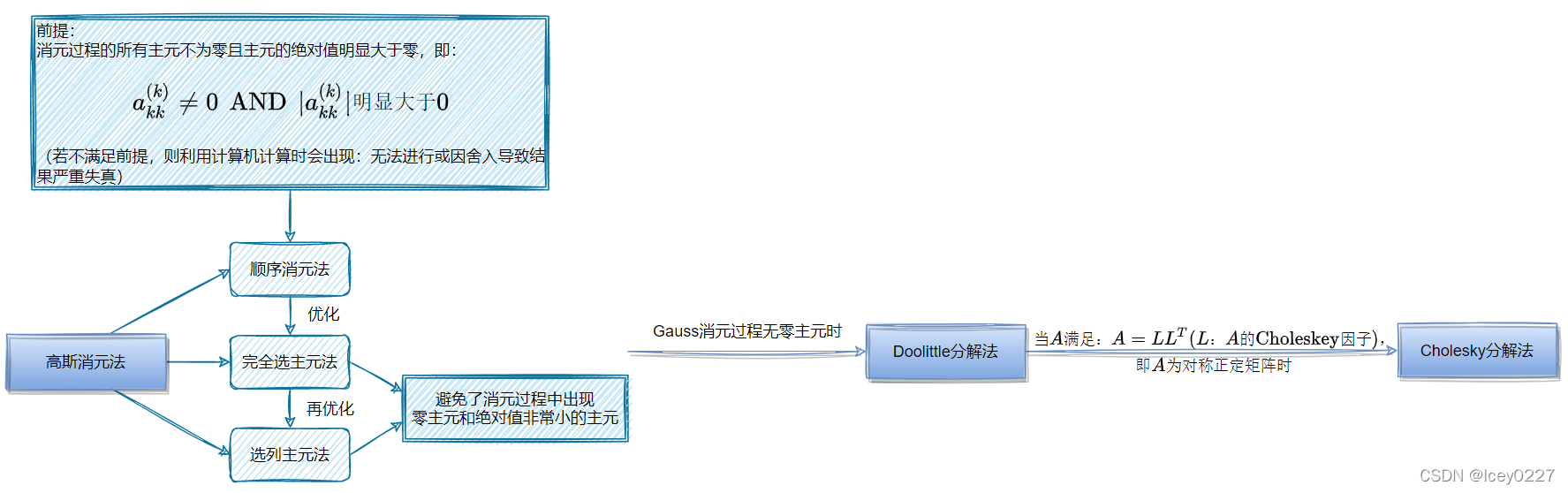
为避免在消元过程中主元为零或绝对值很小的情况，我们对Gauss消元法进行改进—— 完全选主元法 和选列主元法诞生

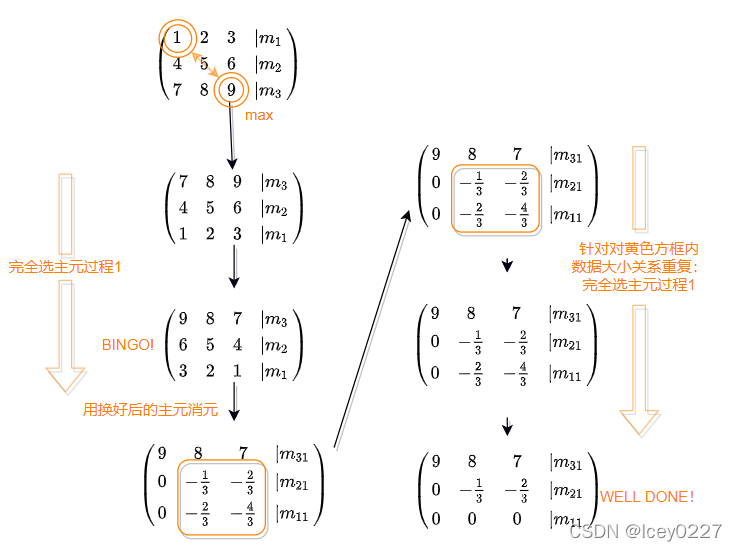
完全选主元法

假设线性方程组：
$$\left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)\left(\begin{array}{c}{m}_1\\ m_2\\ m_3\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)$$
我们要用完全选主元法来求解。
利用下述过程来体现完全选主元的核心思想：

之后进行“回代”求解即可。

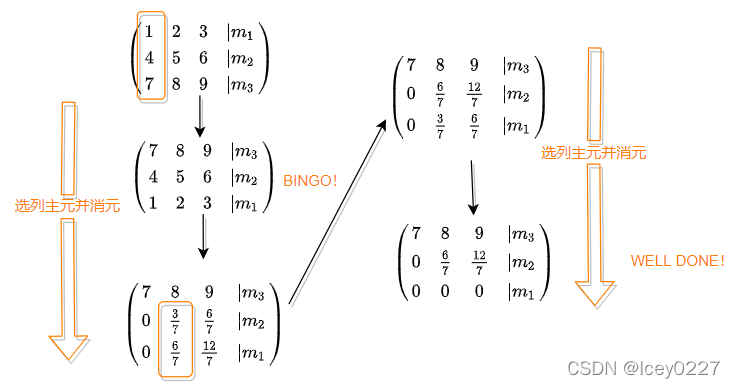
选列主元法

仍假设线性方程组：
$$\left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)\left(\begin{array}{c}{m}_1\\ m_2\\ m_3\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)$$
我们要用选列主元法来求解。
利用下述过程来体现选列主元的核心思想：

之后进行“回代”求解即可。

比较全选主元法和选列主元法，我们很容易发现后者在运算量上更小，选列主元法是更优的Gauss消元法。
在Gauss顺序消元法的基础上我们进一步引进了Doolittle分解法。Doolittle分解法将系数矩阵转化为上三角矩阵和下三角矩阵，节省了Gauss消元过程所需的大量时间和空间。接下来让我们进一步探索Doolittle分解法。

Doolittle分解法

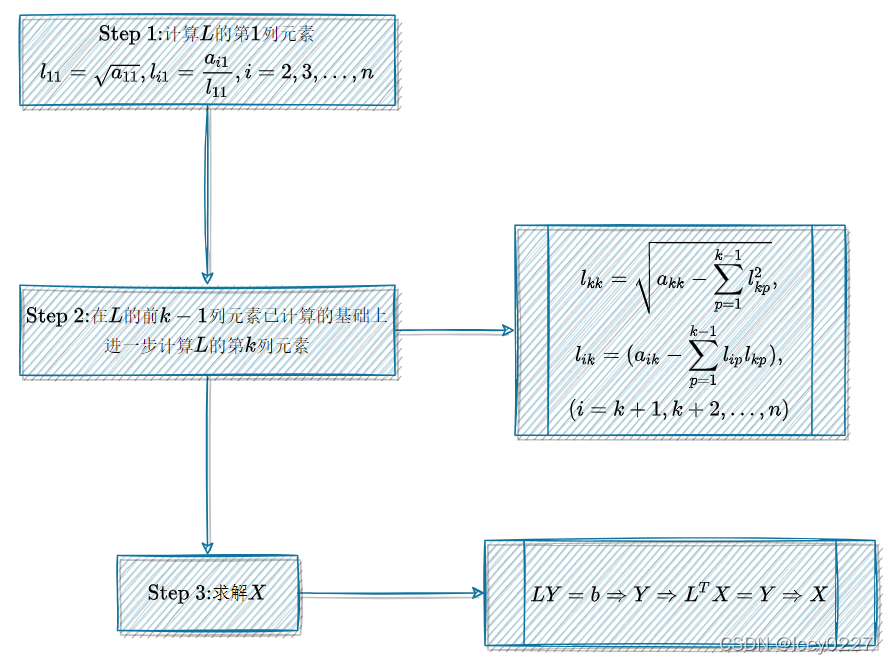
通过Gauss顺序消元法推得Doolittle分解法的过程，我们可以得到：

定理一：
Gauss顺序消元过程中主元素$a_{kk}^{(k)},(k=1,2,\dots ,m)\iff$待求解线性方程组的系数矩阵$A$的$k$阶顺序主子阵$det(A_k)$均非奇异
定理二：
若矩阵$A\in R^{n\times n}$的顺序主子式$det(A_i)\ne 0,(i=1,2,\dots ,n)$,则存在唯一的单位下三角矩阵L及上三角矩阵$U$,使得$A=LU$成立

求解过程：
$$对AX=b：LY=b\Rightarrow Y=(y_1,y_2,\dots ,y_n{)}^T\Rightarrow UX=Y\Rightarrow X$$
对应的MatLab程序：

function x=LUX(A,b)
[n,n]=size(A);
L=zeros(n);U=zeros(n);%用与A相同维度的零矩阵为L、U赋初值
x=zeros(n,1);y=zeros(n,1);
for r=1:n
    for i=r:n
        U(r,i)=A(r,i)-sum(L(r,1:r-1).*U(1:r-1,i)');
        L(i,r)=(A(i,r)-sum(L(i,1:r-1).*U(1:r-1,r)'))/U(r,r);
    end
end

  L,U

for i=1:n
    y(i)=b(i)-sum(L(i,1:i-1).*y(1:i-1)');
end

for j=n:-1:1
    x(j)=(y(j)-sum(U(j,j+1:n).*x(j+1:n)'))/U(j,j);
end
  x
end

矩阵非奇异：方阵且行列式不为0.

Cholesky分解法

Cholesky分解定理：
若矩阵$A$为对称正定矩阵，则存在一个对角元均为正数的下三角矩阵$L\in R^{n\times n}$使得$$A=L{L}^T$$其中$L$称为$A$的Cholesky因子。

最初的 Cholesky分解法

由系数矩阵$A$为对称正定矩阵，可得$A$的所有主子式均为对称正定矩阵。
结合Doolittle分解法 定理2我们可得：
存在唯一单位下三角形矩阵$\tilde{L}=(l_{ij})$及上三角矩阵$U=(u_{ij})$使得$A=\tilde{L}U$
记：$$D=diag(u_{11},u_{22},\dots ,u_{nn})$$
则$\tilde{U}=D^{-1}U$
进一步我们可以得到：
$${\tilde{U}}^{T}D{\tilde{L}}^T=(\tilde{L}U{)}^T=A^T=A=\tilde{L}D\tilde{U}$$
由${\tilde{U}}^{T}D\tilde{L}=\tilde{L}D\tilde{U}\Rightarrow \tilde{U}={\tilde{L}}^T$我们可以得到：$$A=\tilde{L}D{\tilde{L}}^T$$
令$L=\tilde{L}diag(\sqrt{u_{11}},\sqrt{u_{22}},\dots ,\sqrt{u_{nn}}),(l_{ii}=\sqrt{u_{ii}},i=1,2,\dots ,n)$
则$A=L{L}^T$进一步可得：
$$a_{ij}=\sum _{p=1}^{j}lipljp(1\le j\le i\le n)记作（5）式$$
依据$(5)$按列依次计算$L=(l_{ij})$,计算思路如下：

在$\text{Step 2}$中，由于使用了开方运算会占用大量运算时间，我们转换思路：
$$A=L{L}^T\Rightarrow A=\tilde{L}D{\tilde{L}}^T\Rightarrow A=LD{L}^T$$
接下来介绍基于$A=LD{L}^T$所得的改进的Cholesky分解法

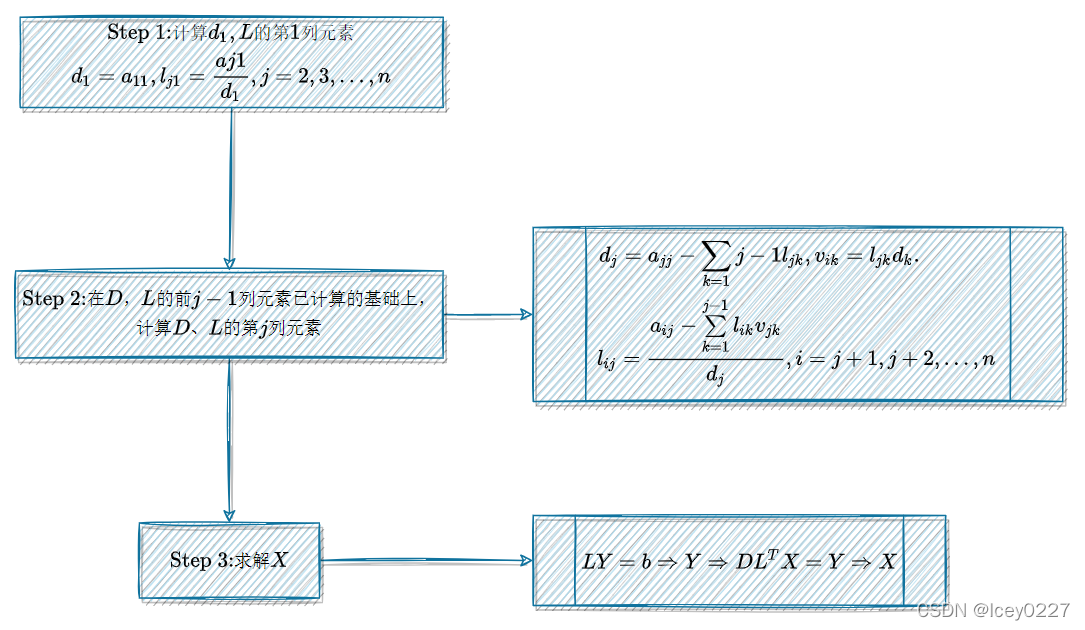
改进的 Cholesky分解法

$$\begin{gathered} A=LD{L}^T \\ 其中： \\ L=(l_{ij})为单位下三角矩阵 \\ D=diag(d_1,d_2,\dots ,d_n)>0 \end{gathered}$$
$$a_{ij}=\sum _{k=1}^{j-1}{l}_{ik}{d}_k{l}_{jk}+l_{ij}{d}_j,1\le j\le i\le n记作（6）式$$
根据$(6)$按列计算$L=(l_{ij})$,计算思路如下：

对应的MatLab程序：

function x=cholesky(a,b)
n=length(b); 
v=zeros(n); 
x=zeros(n,1);
y=zeros(n,1);
for j=1:n
   for i= 1:j-1 
       v(j,i)=a(j,i)*a(i,i);
   end
   a(j,j)=a(j,j)-a(j,1:j-1)*v(j,1:j-1)';
   a(j+1:n,j)=(a(j+1:n,j)-a(j+1:n,1:j-1)*v(j,1:j-1)')/a(j,j);
end
  L=tril(a,-1)+eye(n)
  U=diag(diag(a))*L' 
  for i=1:n
      y(i)=b(i)-L(i,1:i-1)*y(1:i-1);
  end
  for j=n:-1:1
      x(j)=(y(j)-U(j,j+1:n)*x(j+1:n))/U(j,j);
  end
  x
end

追赶法

微分方程的有限元方法、有限差分法以及三次样条函数逼近法等常常产生三对角稀疏型方程组：
$$\left(\begin{array}{ccccccc}{b}_1& c_1& & & & & \\ a_2& b_2& c_2& & & & \\ & \ddots & \ddots & \ddots & & & \\ & & a_i& b_i& c_i& & \\ & & & \ddots & \ddots & \ddots & \\ & & & & a_{n-1}& b_{n-1}& c_{n-1}\\ & & & & & a_n& b_n\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_i\\ ⋮\\ x_{n-1}\\ x_n\end{array}\right)=\left(\begin{array}{c}{d}_1\\ d_2\\ ⋮\\ d_i\\ ⋮\\ d_{n-1}\\ d_n\end{array}\right)$$
其对应的MatLab程序：

function x=chase(a,b,c,d)
n=length(b);
f(1)=c(1)/b(1);
g(1)=d(1)/b(1);
for i=2:n-1
    h(i)=b(i)-f(i-1)*a(i-1);
    f(i)=c(i)/h(i);
    g(i)=(d(i)-g(i-1)*a(i-1))/h(i);
end
g(n)=(d(n)-g(n-1)*a(n-1))/(b(n)-f(n-1)*a(n-1));
x(n)=g(n);
for i=n-1:-1:1
    x(i)=g(i)-f(i)*x(i-1);
end
end

扰动分析

由来

计算过程中的舍入误差，使得输入已知数据带有微小扰动，某些方程对此异常敏感，导致其计算结果产生大的偏差。这些方程被称作病态方程。

定理

设线性方程组$AX=b$的系数矩阵$A$及右端向量b分别带有微小扰动${\delta }_A$和${\delta }_B$，其导出的扰动解$X+{\delta }_X$满足
$$(A+{\delta }_A)(X+{\delta }_X)=b+{\delta }_b$$
则其解具有如下局部相对误差估计：
$$\frac{||{\delta }_X||}{||X||}\le \frac{||A^{-1}||||A||}{1-||A^{-1}||||{\delta }_A||}(\frac{||{\delta }_b||}{b}+\frac{||{\delta }_A||}{||A||})$$
$||A^{-1}||||A||$表征着方程组$AX=b$的解$X$对其系数矩阵A及右端向量变化的敏度，故称之为方程组$AX=b$的条件数，并记作Cond$(A)$。当$\text{Cond}(A)>>1$时，方程组$AX=b$视为病态的。
常用条件数：
Cond 1 ( A ) ≜ ∣ ∣ A − 1 ∣ ∣ 1    ∣ ∣ A ∣ ∣ 1 , Cond ∞ ( A ) ≜ ∣ ∣ A − 1 ∣ ∣ ∞    ∣ ∣ A ∣ ∣ ∞ , Cond 2 ( A ) ≜ ∣ ∣ A − 1 ∣ ∣ 2    ∣ ∣ A ∣ ∣ 2 = max ⁡ 1 ≤ i ≤ n { λ i A T A } min ⁡ 1 ≤ i ≤ n { λ i A T A } , \text{Cond}_1(A)\triangleq||A^{-1}||_1\,\,||A||_1,\\ \text{Cond}_\infty(A)\triangleq||A^{-1}||_\infty\,\,||A||_\infty,\\ \text{Cond}_2(A)\triangleq||A^{-1}||_2\,\,||A||_2=\sqrt{\dfrac{\max\limits_{1\le i\le n}{\{\lambda_{i}^{A^TA}\}}}{\min\limits_{1\le i\le n}{\{\lambda_{i}^{A^TA}\}}}}, Cond1​(A)≜∣∣A−1∣∣1​∣∣A∣∣1​,Cond∞​(A)≜∣∣A−1∣∣∞​∣∣A∣∣∞​,Cond2​(A)≜∣∣A−1∣∣2​∣∣A∣∣2​=1≤i≤nmin​{λiATA​}1≤i≤nmax​{λiATA​}​ ​,
其中，${\lambda }_i^{A^{T}A}$表示矩阵$A^{T}A$的第$i$个特征值。
此外，当矩阵$A$为对称矩阵时，其基于$l_2$范数的条件数可写成：
Cond 2 ( A ) = max ⁡ 1 ≤ i ≤ n { ∣ λ i A ∣ } min ⁡ 1 ≤ i ≤ n { ∣ λ i A ∣ } \text{Cond}_2(A)=\dfrac{\max\limits_{1\le i\le n}\{{|\lambda_{i}^{A}|}\}}{\min\limits_{1\le i\le n}{\{|\lambda_{i}^{A}|}\}} Cond2​(A)=1≤i≤nmin​{∣λiA​∣}1≤i≤nmax​{∣λiA​∣}​
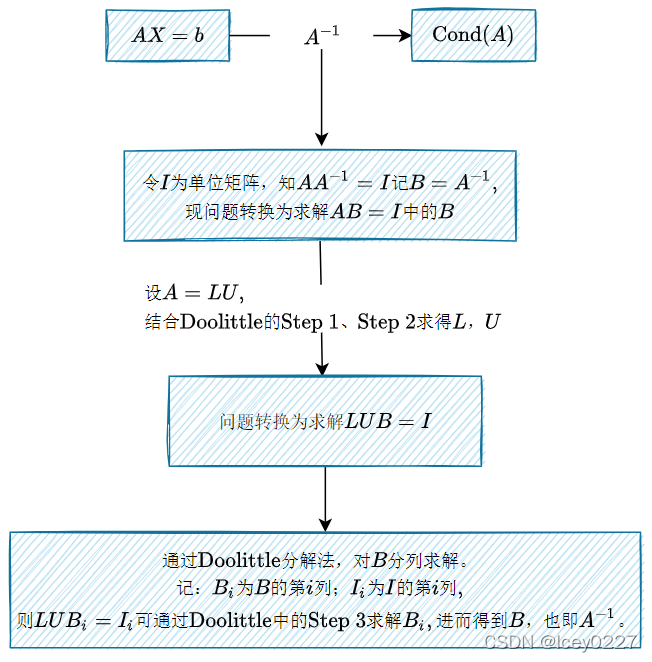
由定理可知，求解条件数的关键:①求解逆矩阵②求解范数

逆矩阵求解

主函数MC_main对应MatLab代码：

A=[10 7 8 7
   7 5 6 5
   8 6 10 9
   7 5 9 10];

n=size(A,1);
L=zeros(n);
U=zeros(n);
B=zeros(n);
I=eye(n);

[L,U]=Matrix_LU(A,n);

for i=1:n
    B(:,i)=MatrixInverse(L,U,I(:,i),n);
end
p=input('请输入条件数对应的范数指标（“1”、“2”、“inf”）\n');
mc=MatrixCondition(A,B,p);
fprintf('该线性方程组对应的条件数为：%e',mc);

求解$L,U$——Matrix_LU对应MatLab代码：

function [L,U]=Matrix_LU(A,n)

L=zeros(n);U=zeros(n);

for r=1:n
    for i=r:n
        U(r,i)=A(r,i)-sum(L(r,1:r-1).*U(1:r-1,i)');
        L(i,r)=(A(i,r)-sum(L(i,1:r-1).*U(1:r-1,r)'))/U(r,r);
    end
end

end

求解矩阵的逆——MatrixInverse对应MatLab代码：

function x=MatrixInverse(L,U,b,n)

x=zeros(n,1);
y=zeros(n,1);

for i=1:n
    y(i)=b(i)-sum(L(i,1:i-1).*y(1:i-1)');
end

for j=n:-1:1
    x(j)=(y(j)-sum(U(j,j+1:n).*x(j+1:n)'))/U(j,j);
end

end

条件数求解——MatrixCondition对应MatLab代码：

function mc=MatrixCondition(A,B,p)

switch p
    case 1
        mc = mnorm1(A)*mnorm1(B);
    case 2
        mc = mnorm2(A)*mnorm2(B);
    case inf
        mc = mnorminf(A)*mnorminf(B);
    otherwise
        error('矩阵范数指标错误！')

end

矩阵范数的求解

在向量空间$R^n(C^n)$中，设$x=(x_1,x_2,\dots ,x_n{)}^T$
常用的向量$x$的范数：

• $x的2范数(欧氏范数)$
  $$||x|{|}_2=(|x_1{|}^2+|x_2{|}^2+\cdots +|x_n{|}^2{)}^{\frac{1}{2}}$$
  二维空间中对应的几何意义：
  $$||x|{|}_2=\sqrt{(y_2-y_1{)}^2+(x_2-x_1{)}^2}$$
  MatLab程序：

  function y = mnorm2(A)
  %矩阵2范数：λ_max（A~TA）
  
  lambda = eig(A'*A);
  lambda_max = max(abs(lambda));
  y = sqrt(lambda_max);
  
  end
  

• $x的1范数$
  $$||x|{|}_1=|x_1|+|x_2|+\cdots +|x_n|$$
  二维空间中对应的几何意义：
  $$||x|{|}_2=|y_2-y_1|+|x_2-x_1|$$

function y = mnorm1(A)
%矩阵1范数：最大列绝对值和

[m,n] = size(A);
x = zeros(1,n);

for j=1:n
    for i=1:m
        x(j) =x(j)+abs(A(i,j));
    end
end
y = max(x);

end

• $x的\infty 范数（最大范数）$
  $$||x|{|}_{\infty }=\underset{1\le i\le n}{\max }|x_i|$$
  二维空间中对应的几何意义：
  $$||x|{|}_{\infty }=max(|y_2-y_1|,|x_2-x_1|)$$

  function y = mnorminf(A)
  %矩阵∞范数：最大行绝对和
  
  [m,n] = size(A);
  x = zeros(m,1);
  
  for i = 1:m
      for j=1:n
          x(i) = x(i) + abs(A(i,j))
      end
  end
  y = max(x);
  
  end
  

  至此，”求精确解部分“的介绍就结束了~