探讨最大公约数和最小公倍数
1.两个数的最大公约数和最小公倍数
一,最大公约数
“lcm 一般是 Least Common Multiple 的缩写,表示最小公倍数。”
”gcd一般指的是G——C——D的小写,表示最大公约数"
如果通过穷举的方法来求两个数的最大公约数,那么可以这样做:
#include<iostream>
#include<cstdio>
using namespace std;
int gcd(int a, int b) //枚举法
{
int max = (a > b) ? a : b;
int min=(a < b) ? a : b;
int ans = 0; //ans是最大公约数
for (int i = min; i >= 2; i--)
{
if (a % i == 0 && b % i == 0)
{
ans = (ans < i) ? i : ans;
}
}
return ans;
}
int main()
{
int a, b;
cin >> a >> b;
cout<< "a和b的最大公约数是:" << gcd(a, b);
return 0;
}
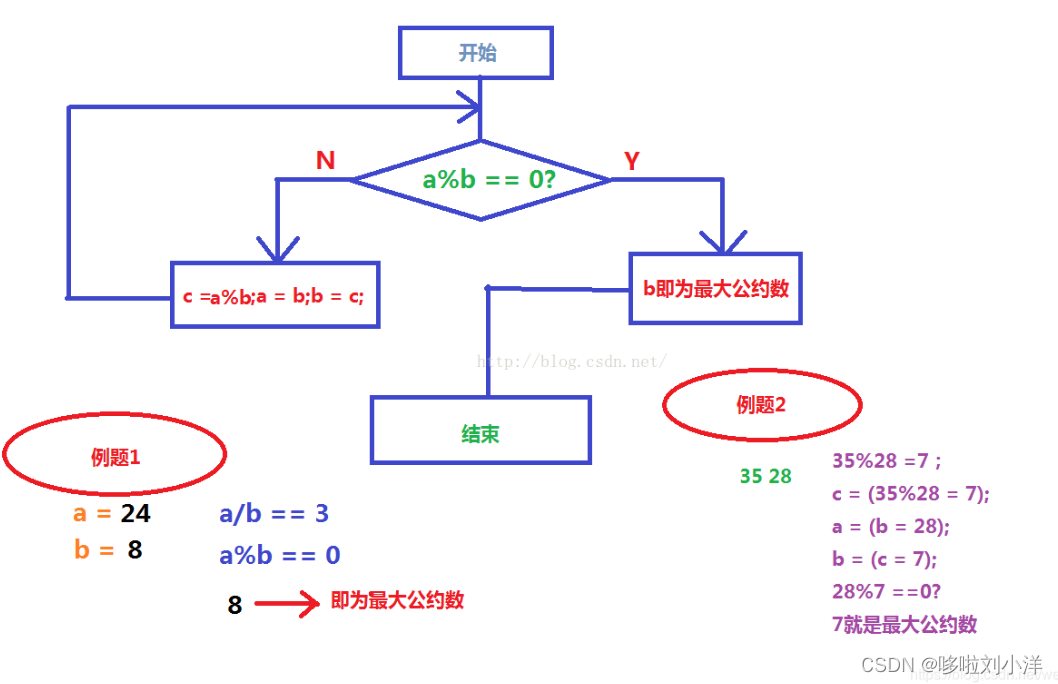
那么发现这种方式非常慢,现在用一种更快捷的方式,叫“辗转相除法”
先说过程:
也就是说:加设a>b,先用a%b=c(b>=c),把b赋值给a,c赋值给b,那么下一次
就是b%c=d(c>=d),把c赋值给b,d赋值给c。那么下一次就是:c%d=e......
一直到n%m==0,那么m就是最大公约数。
证明一下这个结论(反证法):
(1)设两个数a,b(a>b)。gcd(a,b)=c。(c为a,b的最大公约数)
(2)a%b=k…r(这个%指的是数学意义上的除),k是商,r是余数
(3)要证明辗转相除法的合理性,那么要证明gcd(a,b)==gcd(b,r)。也就是证明b,r的最大公约数也是c。
//我们假设b,r的最大公约数不是c。
(4)设a=mc。b=nc。因为r=a-bk=mc-nck=c(m-nk); b=nc;可以看出c是(b,r)的公约数。那么如果要证明c不是(b,r)的最大公约数,那么就要证明,(m-nk)和n这两个数都不是质数,也就是这两个数还可以拆因子给c,让(b,r)的公约数大于c.
(5)假设(m-nk)和n都不是质数,则m-nk=xd,n=yd(d>1),则m=nk+xd=ydk+xd=d(yk+x),a=dc(yk+x),b=dcy,可以看到a,b有公约数dc一定大于c,这是不行的,因为(a,b)的最大公约数c是已知的,所以(m-nk)和n是质数。
(6)因为(m-nk)和n都是质数,那么a=mc。b=nc。因为r=a-bk=mc-nck=c(m-nk); b=nc;可以看出c是(b,r)的最大公约数。所以(b,c)和(a,b)的最大公约数都是c,所以辗转相除法是有依据的求最大公约数的方法
(7)证明完毕
下面是代码
#include<iostream>
#include<cstdio>
using namespace std;
//int gcd(int a, int b) //不用递归(辗转相除法)
//{
// int c = b;
// while (a % b != 0)
// {
// c = a % b;
// a = b;
// b = c;
// }
// return c;
//}
int gcd(int a, int b) //用递归(辗转相除法)
{
int max=(a>b)?a:b;
int min=(a<b)?a:b;
if (max % min == 0)
return min;
if (max > min)
{
return gcd(min, max % min);
}
}
int main()
{
int a, b;
cin >> a >> b;
cout<< "a和b的最大公约数是:" << gcd(a, b);
return 0;
}
二,最小公倍数
知道最大公约数就知道最小公倍数了。
因为如果找到了两个数a,b的最大公约数c,那么假设a=mc,b=nc,那么可以肯定,n,m没有公约数,这里暂且称之为“互质数”,即m,n相互之间的关系相当于两个质数之间的关系。那么求a,b的最小公倍数,就相当于求m,n的最小公倍数。我们令mx=ny=c, 则m/n=y/x。则y=km,x=kn。要使mx最小,也就是ny最小,则mkn最小,则k=1时mkn最小,则mn最小,同理,ny当y=m时也最小,所以n,m的最小公倍数就是nm。
所以结论是:a,b的最小公倍数就是m * n * c,
下面是代码
#include<iostream>
#include<cstdio>
using namespace std;
#include<iostream>
#include<cstdio>
using namespace std;
//int gcd(int a, int b) //枚举法
//{
// int max = (a > b) ? a : b;
// int min=(a < b) ? a : b;
// int ans = 0; //ans是最大公约数
// for (int i = min; i >= 2; i--)
// {
// if (a % i == 0 && b % i == 0)
// {
// ans = (ans < i) ? i : ans;
// }
// }
// return ans;
//}
//int gcd(int a, int b) //不用递归(辗转相除法)
//{
// int c = b;
// while (a % b != 0)
// {
// c = a % b;
// a = b;
// b = c;
// }
// return c;
//}
int gcd(int a, int b) //用递归(辗转相除法)
{
int max=(a>b)?a:b;
int min=(a<b)?a:b;
if (max % min == 0)
return min;
if (max > min)
{
return gcd(min, max % min);
}
}
int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
int main()
{
int a, b,c;
cin >> a >>b;
int max, min;
if (a > b)
{
max = a;
min = b;
}
else
{
max = b;
min = a;
}
cout << gcd(max,min);
}
2.三个数的最大公约数和最小公倍数
要运动了,明天更新😎😎💓💓
我来了!
三个数的的最大公约数:
- 假设三个数a,b,c
- 先求a,b的最大公约数x
- 再求x,c的最大公约数y
- y就是a,b,b的最大公约数
#include<iostream>
#include<cstdio>
using namespace std;
//int gcd(int a, int b) //枚举法
//{
// int max = (a > b) ? a : b;
// int min=(a < b) ? a : b;
// int ans = 0; //ans是最大公约数
// for (int i = min; i >= 2; i--)
// {
// if (a % i == 0 && b % i == 0)
// {
// ans = (ans < i) ? i : ans;
// }
// }
// return ans;
//}
//int gcd(int a, int b) //不用递归(辗转相除法)
//{
// int c = b;
// while (a % b != 0)
// {
// c = a % b;
// a = b;
// b = c;
// }
// return c;
//}
int gcd(int a, int b) //用递归(辗转相除法)
{
int max=(a>b)?a:b;
int min=(a<b)?a:b;
if (max % min == 0)
return min;
if (max > min)
{
return gcd(min, max % min);
}
}
int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
int main()
{
int a, b,c;
cin >> a >> b>>c; //a要大于b
cout << "三个数的最大公约数是:";
int max,min;
if (gcd(a, b) > c)
{
max = gcd(a, b);
min = c;
}
else
{
max = c;
min = gcd(a, b);
}
cout << gcd(max, min);
return 0;
}
那么三个数的最小公倍数呢?
这个比较难理解,说实话我也是懵懵懂懂。但是用这种方式没有错了:假设3个数a,b,c。先求a,b的最小公倍数x,然后求x和c的最小公倍数y,那么y就是a,b,c的最小公倍数。这个可以当成结论来写。
由此结论写出三个数或三个数以上求最小公倍数的方法
#include<iostream>
using namespace std;
int a[1000];
int gcd(int a, int b)
{
int max = (a > b) ? a : b; //始终保持除数大于被除数
int min = (a < b) ? a : b;
int ans = min;
while (max % min != 0)
{
ans =max%min;
max=min;
min = ans;
}
return ans;
}
int lcd(int a, int b)
{
return a / gcd(a, b) * b;
}
int main()
{
int n; //求几个数的最小公倍数
cin >> n;
for (int i = 1; i <= n; i++) //3 9 7 6 89 43 14 56
cin >> a[i];
int ans = a[1];
for (int i = 1; i < n; i++) //假如3个数求最小公倍数,那么只要求两次,先求前两个的最小公倍数,然后求前两个的最小公倍数和最后一个数的最小公倍数
{
ans = ans / gcd(ans, a[i+1]) * a[i+1]; //lcm=a*b/gcd(a,b)=a/gcd(a,b)*b; lcm是最小公倍数,gcd是最大公约数
}
cout<<n<<"个数的最小公倍数是:";
cout << ans;
return 0;
}
总结:1.当求最大公约数的时候,一定要先预处理,保证大的数放前面,小的数放后面。
2.求多个数的最小公倍数还是略有生疏,主要是不知道为什么要这么做。虽然自己伪证明了一下,但是逻辑不完整。但先这样吧。