深度神经网络

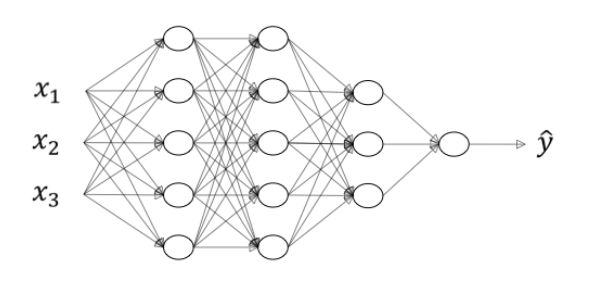
1. 这是一个深度神经网络

   

   用 $L=4$ 表示神经网络层数，用 $n^{[l]}$ 表示第 $l$ 层神经元数量，有 $n^{[1]}=n^{[2]}=5$， $n^{[3]}=3$， $n^{[4]}=n^{[L]}=1$， $n^{[0]}=n_x=3$。

   对于前向传播有：

   $$\begin{gathered} z^{[l]}={\omega }^{[l]}{a}^{[l-1]}+b^{[l]} \\ {a}^{[l]}=g^{[l]}(z^{[l]}) \end{gathered}$$

   向量化实现：

   $$\begin{gathered} Z^{[l]}={\omega }^{[l]}{A}^{[l-1]}+b^{[l]} \\ {A}^{[l]}=g^{[l]}(Z^{[l]}) \end{gathered}$$

   前向传播需要输入 $A^{[l-1]}$ ，输出 $A^{[l]}$，缓存 $Z^{[l]}$， ${\omega }^{[l]}$， $b^{[l]}$。

   对于反向传播有：

   $$\begin{gathered} d{z}^{[l]}=d{a}^{[l]}\ast {g^{[l]}}^{\prime }(z^{[l]}) \\ d{w}^{[l]}=d{z}^{[l]}\cdot a^{[l-1]} \\ d{b}^{[l]}=d{z}^{[l]} \\ d{a}^{[l-1]}=w^{\left[l\right]T}\cdot {dz}^{[l]} \\ d{z}^{[l]}=w^{[l+1]T}d{z}^{[l+1]}\cdot {g^{[l]}}^{\prime }(z^{[l]}) \end{gathered}$$

   向量化实现：

   $$\begin{gathered} d{Z}^{[l]}=d{A}^{[l]}\ast {g^{\left[l\right]}}^{\prime }\left(Z^{[l]}\right) \\ d{\omega }^{[l]}=\frac{1}{m}d{Z}^{[l]}{A}^{\left[l-1\right]T} \\ d{b}^{[l]}=\frac{1}{m}\sum d{Z}^{[l]} \\ d{A}^{[l-1]}={\omega }^{\left[l\right]T}d{Z}^{[l]} \end{gathered}$$

   dbl = 1. / m * np.sum(dZl, axis=1, keepdims=True)

   反向传播需要输入 $d{A}^{[l]}$和缓存的数据，输出 $d{\omega }^{[l]}$， $d{b}^{[l]}$和 $d{A}^{[l-1]}$。

2. 当实现深度神经网络的时候，一个常用的检查代码是否有错的方法就是过一遍算法中矩阵的维数。

   $$\begin{gathered} {\omega }^{[l]}\in {\mathbb{R}}^{n^{[l]}\times n^{[l-1]}}{A}^{[l-1]}\in {\mathbb{R}}^{n^{[l-1]}\times m}{b}^{[l]}\in {\mathbb{R}}^{n^{[l]\times m}} \\ {Z}^{[l]}={\omega }^{[l]}{A}^{[l-1]}+b^{[l]} \\ {Z}^{[l]}\in {\mathbb{R}}^{n^{[l]\times m}}{A}^{[l]}\in {\mathbb{R}}^{n^{[l]\times m}} \\ {A}^{[l]}=g^{[l]}(Z^{[l]}) \end{gathered}$$

   $$\begin{gathered} d{A}^{[l]}\in {\mathbb{R}}^{n^{[l]}\times m}{Z}^{[l]}\in {\mathbb{R}}^{n^{[l]}\times m} \\ d{Z}^{[l]}=d{A}^{[l]}\ast {g^{\left[l\right]}}^{\prime }\left(Z^{[l]}\right) \\ d{Z}^{[l]}\in {\mathbb{R}}^{n^{[l]}\times m}{A}^{[l-1]}\in {\mathbb{R}}^{n^{[l-1]}\times m}d{\omega }^{[l]}\in {\mathbb{R}}^{n^{[l]}\times n^{[l-1]}} \\ d{\omega }^{[l]}=\frac{1}{m}d{Z}^{[l]}{A}^{\left[l-1\right]T} \\ d{b}^{[l]}\in {\mathbb{R}}^{n^{[l]}\times 1} \\ d{b}^{[l]}=\frac{1}{m}\sum d{Z}^{[l]} \\ {\omega }^{[l]}\in {\mathbb{R}}^{n^{[l]}\times n^{[l-1]}}d{Z}^{[l]}\in {\mathbb{R}}^{n^{[l]}\times m}d{A}^{[l-1]}\in {\mathbb{R}}^{n^{[l-1]}\times m} \\ d{A}^{[l-1]}={\omega }^{\left[l\right]T}d{Z}^{[l]} \end{gathered}$$

3. 深度神经网络通过多层的隐藏单元逐步从输入数据中提取特征。每一层的神经元负责学习不同级别的特征，随着层数的增加，网络可以逐步从简单的局部特征（如图像中的边缘）学习到更复杂的全局特征（如面部各个部位或对象的整体结构）。

   在人脸检测中，网络的逐层学习过程：

   1. 第一层（低级特征探测）
      在输入层之后，第一层的神经元主要负责捕捉输入数据中的低级特征。例如，在图像处理中，第一层的神经元可以学习到图像中的边缘（如垂直或水平的边缘）。这类似于你提到的“边缘探测器”或“特征探测器”。
   2. 中间层（组合低级特征）:
      后续的层开始将这些低级特征组合成更复杂的局部特征。例如，第二层或第三层的神经元可能将边缘结合起来，识别图像中的某些面部特征，如眼睛、鼻子等。这些层捕捉的是数据的“中级特征”。
   3. 高层（高级特征和全局理解）
      在深层的网络中，神经元将前面学到的局部特征组合起来，形成对整个对象的理解。在人脸识别任务中，这些层可能将眼睛、鼻子、嘴巴等组合起来，最终识别出整张面部图像。

   在网络中，深度指的是神经网络的层数。更深的网络可以捕捉到更多的层级特征，逐步构建出复杂的表示。宽度指的是每一层的神经元数量。在深层网络中，层数相对较多，但每一层的神经元数量相对较少；如果要用浅层网络来模拟深层网络，通常需要大幅增加每一层的神经元数量，甚至达到指数级增长。

   深度神经网络的强大之处在于它可以从简单的特征（如边缘）开始，逐层学习到更复杂的模式。通过这种逐步的特征提取，网络能够有效地解决复杂的任务，如人脸识别、语音识别等。

4. 在机器学习中，超参数是指那些在训练过程中不能通过模型自我学习得到的参数，而是由开发者手动设置的参数。这些参数的选择对模型的性能有重要影响。常见的超参数包括：

   • 学习率 (Learning Rate)：决定每次参数更新的幅度。如果学习率过高，模型可能会错过最优解；如果学习率过低，模型可能会收敛过慢。
   • 梯度下降法的循环轮数 (Epochs)：指模型训练时完整遍历数据集的次数。更多的训练轮数通常有助于提高模型的准确度，但也可能导致过拟合。
   • 隐藏层数目 (Number of Hidden Layers)：决定了神经网络的深度。更深的网络可以学习更复杂的特征，但也可能增加计算复杂度和过拟合的风险。
   • 每层神经元的数量 (Number of Neurons in Each Layer)：影响每层的表示能力。更多的神经元可以增强模型的表达能力，但也增加了计算量和可能的过拟合问题。
   • 激活函数 (Activation Function)：决定了每一层神经元输出的非线性特征。常见的激活函数包括ReLU、Sigmoid、Tanh等，选择合适的激活函数有助于网络的有效学习。

   这些超参数通常是通过手动设置的，并且会影响到模型的训练效果和最终的性能，因此它们被称作超参数。

5. 寻找超参数的最优值通常不是通过简单的公式计算得到，而是依赖于大量的实验和调试。一般来说，超参数优化的过程可以概括为一个 Idea — Code — Experiment — Idea 的迭代循环。

   • Idea：根据问题的需求和经验，提出一组超参数的初步选择。比如选择合适的学习率、隐藏层数、激活函数等。
   • Code：根据初步的超参数选择，编写和实现模型。
   • Experiment：运行模型并观察它的表现，通常通过验证集上的性能来衡量模型是否有效。根据实验结果，你可能会发现模型没有达到预期的效果，或者存在过拟合、欠拟合等问题。
   • Idea：根据实验结果调整超参数。可能是尝试不同的学习率、增加或减少隐藏层数量、选择不同的激活函数等，以改善模型的性能。

   然后再进入下一轮循环。每一轮的实验和反馈都帮助你更精确地选择最优的超参数组合。

   在实践中，为了高效寻找最优的超参数组合，可以使用一些自动化的方法，比如：

   • 网格搜索 (Grid Search)：通过穷举不同超参数的所有可能组合，找到最优的超参数。
   • 随机搜索 (Random Search)：在超参数的空间内随机选择组合，进行多次实验，虽然可能不如网格搜索精确，但计算成本较低。
   • 贝叶斯优化 (Bayesian Optimization)：使用概率模型来选择超参数，逐步调整以优化目标函数，通常能在较少的实验次数内找到好的超参数。

6. 在计算前向传播时，我们需要使用for循环计算1到L层，要记住range是左开右闭区间。

   for i in range(1, L+1)