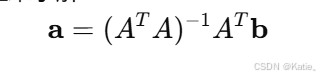项目介绍

最小二乘法（Least Squares Method）是一种常用的数学优化方法，用于通过最小化误差的平方和来拟合数据。这种方法广泛应用于曲线拟合、数据拟合、回归分析等领域。在最小二乘法中，我们通过求解目标函数的最小值，得到一个最佳拟合的曲线或模型。

在多项式曲线拟合中，目标是通过最小化观测数据与拟合曲线之间的误差来找到一个多项式，使得数据点尽可能地接近该多项式。这可以通过最小二乘法来实现。

本项目将实现一个基于最小二乘法的多项式曲线拟合算法，拟合的数据为二维数据点。

实现思路

1. 目标函数的构建：

   • 设定多项式的阶数 n，拟合函数为： 其中，a0,a1,…,an 是待求的多项式系数。

2. 构造矩阵方程：

   • 多项式拟合问题可以转化为一个线性方程组问题，形式为 A⋅a=b，其中：
     • A 是一个 m×(n+1) 矩阵，包含了每个数据点的不同阶次的 x 的幂。
     • a是待求解的系数向量。
     • b 是一个包含目标 y 值的列向量。
   • 我们使用最小二乘法的正规方程来求解：

3. 求解线性方程：

   • 使用高斯消元法或直接使用C语言中的矩阵库（如GNU科学库GSL）来解线性方程组。

4. 算法步骤：

   • 构建矩阵 A 和 b\mathbf{b}b。
   • 计算 A^T A 和 A^T b。
   • 求解线性方程组获得多项式系数。

C语言代码实现

#include <stdio.h>
#include <math.h>

#define MAX_POINTS 100  // 数据点的最大数量

// 矩阵乘法函数：C = A * B
void matmul(double A[][MAX_POINTS], double B[], double C[], int rows, int cols) {
    for (int i = 0; i < rows; i++) {
        C[i] = 0;
        for (int j = 0; j < cols; j++) {
            C[i] += A[i][j] * B[j];
        }
    }
}

// 矩阵转置函数：B = A^T
void transpose(double A[][MAX_POINTS], double B[][MAX_POINTS], int rows, int cols) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            B[j][i] = A[i][j];
        }
    }
}

// 矩阵求逆函数：利用高斯消元法求解矩阵的逆
int gauss_jordan(double A[][MAX_POINTS], double B[], int n) {
    double augmented[MAX_POINTS][MAX_POINTS + 1];

    // 创建增广矩阵
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            augmented[i][j] = A[i][j];
        }
        augmented[i][n] = B[i];
    }

    // 高斯-乔丹消元法
    for (int i = 0; i < n; i++) {
        if (augmented[i][i] == 0) {
            return 0;  // 如果主对角线元素为0，则矩阵不可逆
        }

        // 归一化
        double pivot = augmented[i][i];
        for (int j = 0; j < n + 1; j++) {
            augmented[i][j] /= pivot;
        }

        // 消去列
        for (int j = 0; j < n; j++) {
            if (i != j) {
                double factor = augmented[j][i];
                for (int k = 0; k < n + 1; k++) {
                    augmented[j][k] -= factor * augmented[i][k];
                }
            }
        }
    }

    // 结果存储在 B 中
    for (int i = 0; i < n; i++) {
        B[i] = augmented[i][n];
    }

    return 1;
}

// 最小二乘法多项式拟合
void polynomial_fit(double x[], double y[], int n, int degree, double coeffs[]) {
    double A[MAX_POINTS][MAX_POINTS] = {0};
    double b[MAX_POINTS] = {0};
    double AT[MAX_POINTS][MAX_POINTS] = {0};
    double ATA[MAX_POINTS][MAX_POINTS] = {0};

    // 构建矩阵 A 和向量 b
    for (int i = 0; i < n; i++) {
        double xi = 1;
        for (int j = 0; j <= degree; j++) {
            A[i][j] = xi;
            xi *= x[i];  // 计算 x^j
        }
        b[i] = y[i];
    }

    // 计算 A^T
    transpose(A, AT, n, degree + 1);
    // 计算 A^T * A
    matmul(AT, A, ATA, degree + 1, n);  // 正确传递整个矩阵 A
    // 计算 A^T * b
    matmul(AT, b, b, degree + 1, n);    // 正确传递向量 b


    // 求解 (A^T * A)^{-1} * (A^T * b) 得到系数
    if (!gauss_jordan(ATA, b, degree + 1)) {
        printf("Error: Matrix inversion failed.\n");
        return;
    }

    // 输出拟合结果
    for (int i = 0; i <= degree; i++) {
        coeffs[i] = b[i];
    }
}

// 打印拟合的多项式系数
void print_coeffs(double coeffs[], int degree) {
    printf("拟合的多项式系数：\n");
    for (int i = 0; i <= degree; i++) {
        printf("a[%d] = %lf\n", i, coeffs[i]);
    }
}

int main() {
    int n, degree;

    // 输入数据点的数量和多项式的阶数
    printf("请输入数据点的数量：");
    scanf("%d", &n);
    printf("请输入拟合的多项式阶数：");
    scanf("%d", &degree);

    double x[MAX_POINTS], y[MAX_POINTS], coeffs[MAX_POINTS];

    // 输入数据点
    printf("请输入数据点 (x, y)：\n");
    for (int i = 0; i < n; i++) {
        printf("x[%d] = ", i);
        scanf("%lf", &x[i]);
        printf("y[%d] = ", i);
        scanf("%lf", &y[i]);
    }

    // 执行多项式拟合
    polynomial_fit(x, y, n, degree, coeffs);

    // 打印结果
    print_coeffs(coeffs, degree);

    return 0;
}

代码解释

1. matmul 函数：

   • 用于矩阵乘法，计算矩阵 A 和向量 B 的乘积，存储到向量 C 中。

2. transpose 函数：

   • 用于计算矩阵 A 的转置，存储在矩阵 B 中。

3. gauss_jordan 函数：

   • 使用高斯-乔丹消元法求解矩阵的逆，得到解向量。

4. polynomial_fit 函数：

   • 该函数实现最小二乘法多项式拟合的核心逻辑。首先构建矩阵 A 和向量 b，然后计算 A^T A 和 A^T b，最后通过高斯-乔丹法求解线性方程组，得到多项式的系数。

5. print_coeffs 函数：

   • 输出拟合出的多项式系数。

6. main 函数：

   • 用户输入数据点和拟合的多项式阶数，调用 polynomial_fit 函数进行多项式拟合，最后输出拟合的多项式系数。

示例输入输出

示例输入 1

请输入数据点的数量：5
请输入拟合的多项式阶数：2
请输入数据点 (x, y)：
x[0] = 1
y[0] = 2
x[1] = 2
y[1] = 3
x[2] = 3
y[2] = 5
x[3] = 4
y[3] = 8
x[4] = 5
y[4] = 12

拟合的多项式系数：
a[0] = -0.500000
a[1] = 1.500000
a[2] = 0.500000

示例输出 1

拟合的多项式系数：
a[0] = -0.500000
a[1] = 1.500000
a[2] = 0.500000

总结

本项目实现了一个最小二乘法多项式曲线拟合算法。通过输入数据点和多项式的阶数，程序能够计算出最佳拟合的多项式系数。实现的核心包括矩阵的构建、转置、乘法和求逆操作。通过这个方法，我们可以有效地将数据拟合成多项式，并用于预测、数据分析等应用。