一、前言

🗨️个人介绍：

⚓大家好，我是李逢溪，是一个热爱计算机技术的非内卷者，酷爱游戏设计，未来希望从事游戏开发行业，欢迎大家与我一起交流进步✊！

今天向大家介绍一类特殊的数据结构——堆，希望能够帮助到大家！

本章重点：

• 堆的介绍
• 堆的接口实现
• 堆排序

二、堆

2.1堆的介绍

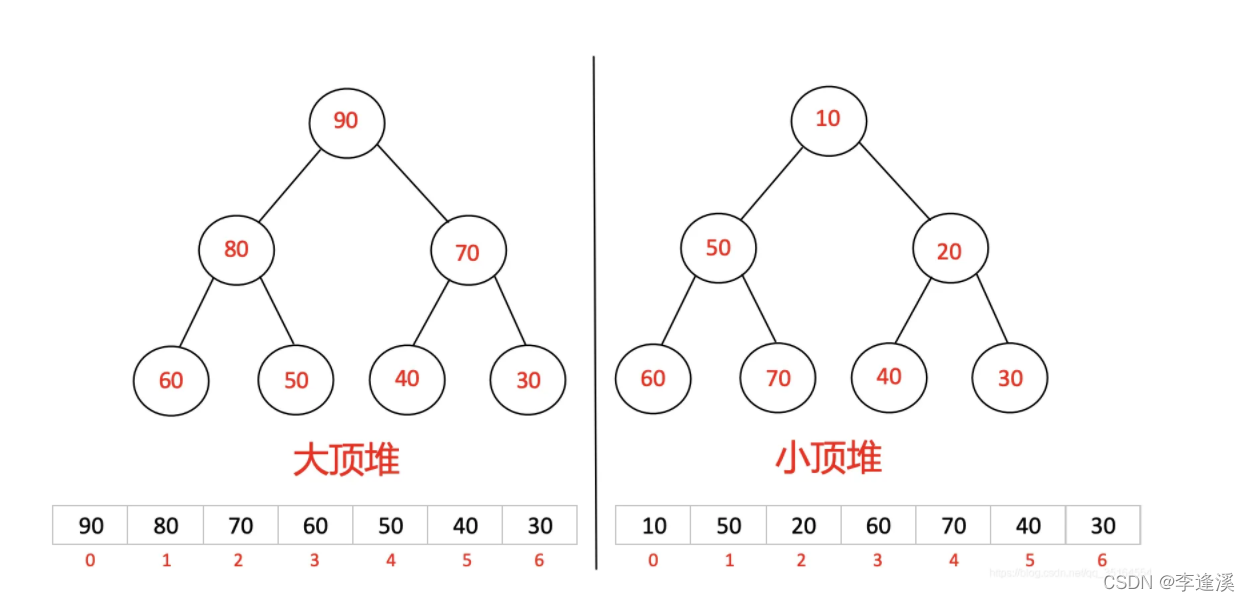
一般来说，堆在物理结构上是连续的数组结构，在逻辑结构上是一颗完全二叉树。

但要满足

• 每个父亲节点的值都得大于孩子节点的值，这样的堆称为大堆。
• 每个父亲节点的值都得小于孩子节点的值，这样的堆称为小堆。

那么以下就是一个小堆。

百度百科：

堆的定义如下：n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时，称之为堆。

若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。由此，若序列{k1,k2,…,kn}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。 

💯下面序列是堆的是( )。 

A．97，56，38，66，23，42，12 //不是大堆也不是小堆，即不是堆。

B．23，86，48，3，35，39，42 //不是大堆也不是小堆，即不是堆。

C．05，56，20，23，40，38，29  //不是大堆也不是小堆，即不是堆。

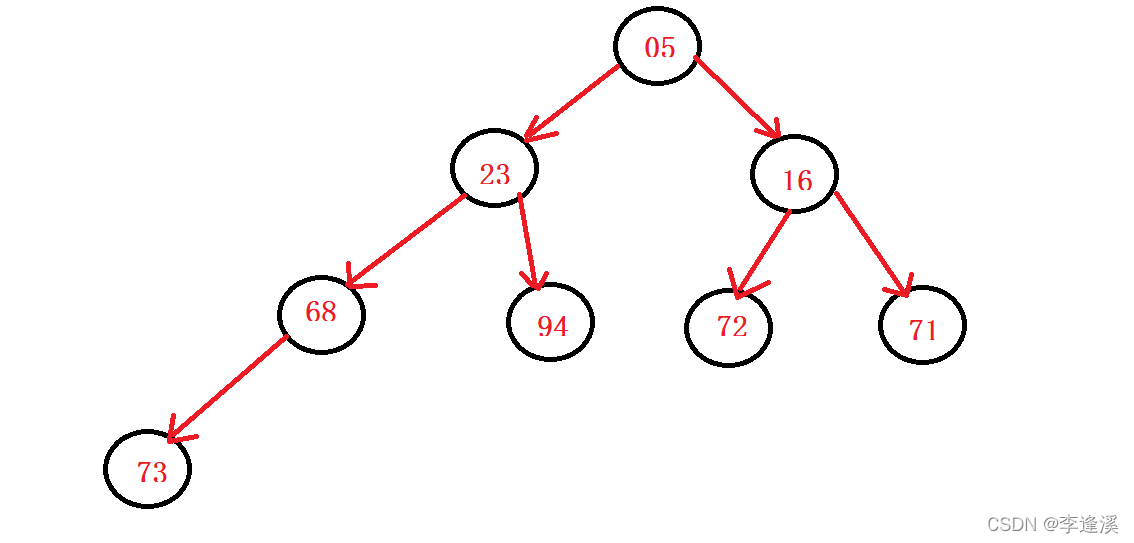
D．05，23，16，68，94，72，71，73  //是小堆

只有D是堆而且是小堆，因此答案选D。

D的逻辑结构：

 父亲节点和孩子节点的数组下标有以下关系：

1. left_child=(parent+1)*2

2. right_child=(parent+2)*2

3. parent=（child-1）/2（这里的child左孩子和右孩子都适用）

以上就不做证明了，不过我们可以验证一下，以上图D的逻辑结构为例，16的parent下标是2，72的下标是5，71的下标是6，满足left_child=(parent+1)*2、right_child=(parent+2)*2、parent=（child-1）/2。

有序一定是堆，堆不一定有序。

同时堆顶的数组是整个数组最大的数或者整个数组最小的数。

2.2堆的接口实现

第一件事我们就是要创建堆，实际就是创建一个数组，这里用动态数组。

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	size_t size;
	size_t capacity;
}HP;

堆创建好之后，我们需要对它进行初始化。

🌺第一个接口：

void HeapInit(HP* php);

轻车熟路，将堆中的a置为NULL，size和capacity置为0。

或者这里可以设置capacity不为0的初始值也是可以的。

🌴参考代码：

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
}

我们对堆进行初始化之后，也要在最后销毁堆。

🌺第二个接口：

void HeapDestroy(HP* php)

销毁堆，即销毁一个动态数组

🌴参考代码：

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

现在我们可以考虑往堆中插入数据了，要求插入新元素之后还是堆。

🌺第三个接口：

void HeapPush(HP* php, HPDataType x)

堆没有要求在哪个位置插入新元素，可以在任意的位置插入新元素，但要保证插入新元素之后还是堆。

由于数组在头部还是在中间位置的插入复杂度是O（N），并且插入后不一定是堆了。

因此我们考虑的是直接在数组尾部插入新元素，然后用一个函数去调整数组的顺序使得它还是一个堆。

那么核心代码就是这个调整算法。

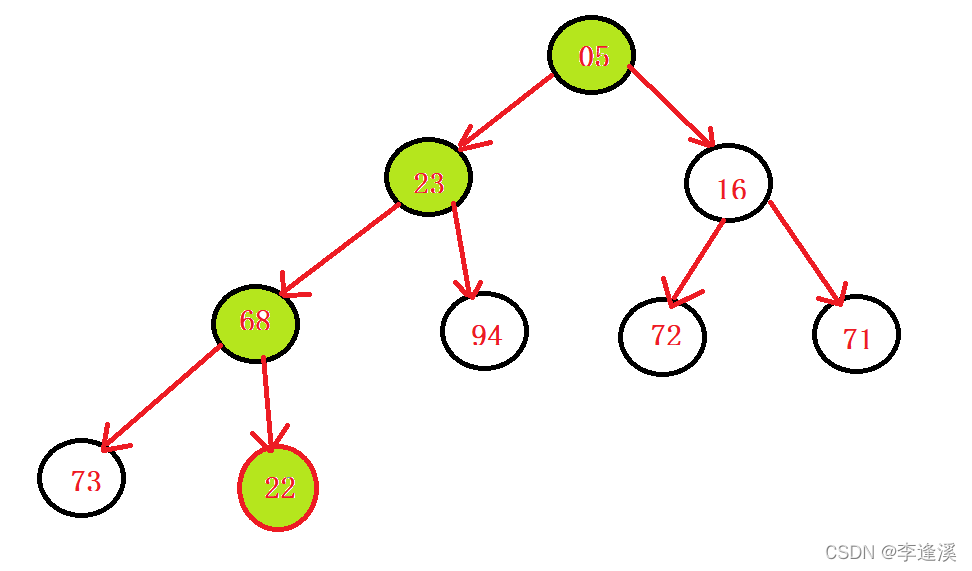
先来看这一个堆，插入新元素后该如何进行调整。

 我们在数组的最后插入22，原堆是一个小堆，此时我们需要从下往上去调整各个父亲节点，使得该堆还是一个小堆。

换句话说：我们只需要调整下面有彩色的节点顺序。

交换过程：如果孩子节点小于父亲节点，那么将它们交换，然后迭代。

如果孩子节点大于父亲节点就跳出循环。

迭代过程：将父亲节点的下标赋值给孩子节点的下标，然后重新计算父亲节点的下标，计算方法：parent=（child-1）/2。

🌴参考代码：

void AdjustUp(HPDataType* a, size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
        //如果孩子小于父亲，则交换    
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
        //孩子大于父亲，则结束调整
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
    //动态数组，空间不够要扩容

	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType)* newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}

		php->a = tmp;
		php->capacity = newCapacity;
	}
    //尾插数据
	php->a[php->size] = x;
	++php->size;

	// 向上调整，控制保持是一个小堆
	AdjustUp(php->a, php->size - 1);
}

上面是多个数据的插入，那么如果插入第一个数据，这个函数还能帮助我们把数据插入堆中吗？

答案是肯定的。

既然有Push数据到堆，自然有从堆中删除元素了。

这里的删除不同于栈和队列的删除，这里指的是将堆顶的数据删除，删除之后堆还是一个堆。为什么只实现删堆顶的数据，因为简单实用，这个接口是为后面的堆排序做准备的。

🌺第四个接口：

void HeapPop(HP* php)

思路比较简单：将数组第一个元素删除，然后保持它还是一个小堆。

怎么删除第一个数据呢？

这里的考虑是将数组第一个元素和数组最后一个交换，交换之后尾删掉最后一个元素，达成删除第一个元素的效果，复杂度是O（N），这里可以提一下，这种头删的方式是改变了数组元素的相对顺序的。

删除之后我们要做调整，使得堆还是小堆。

那么怎么调整呢？

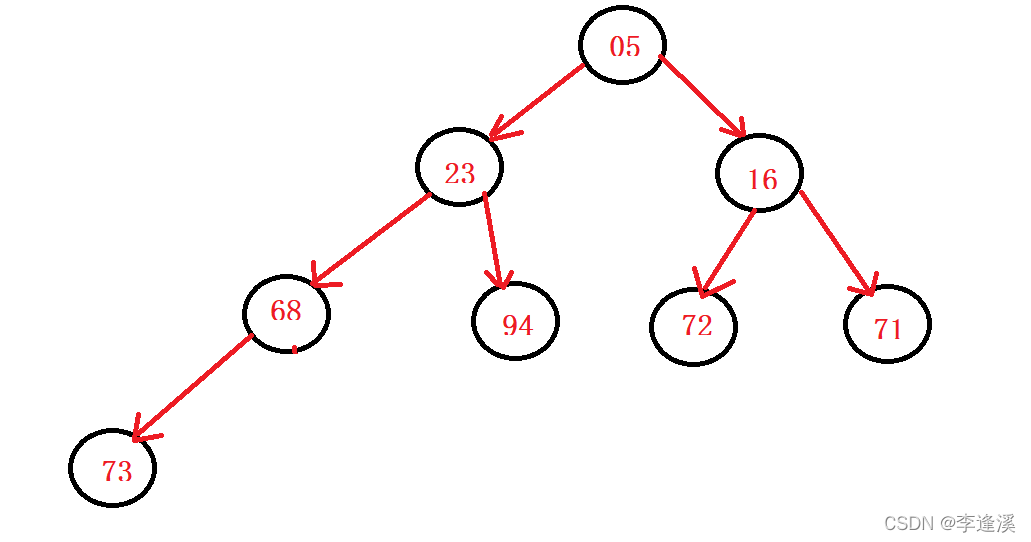
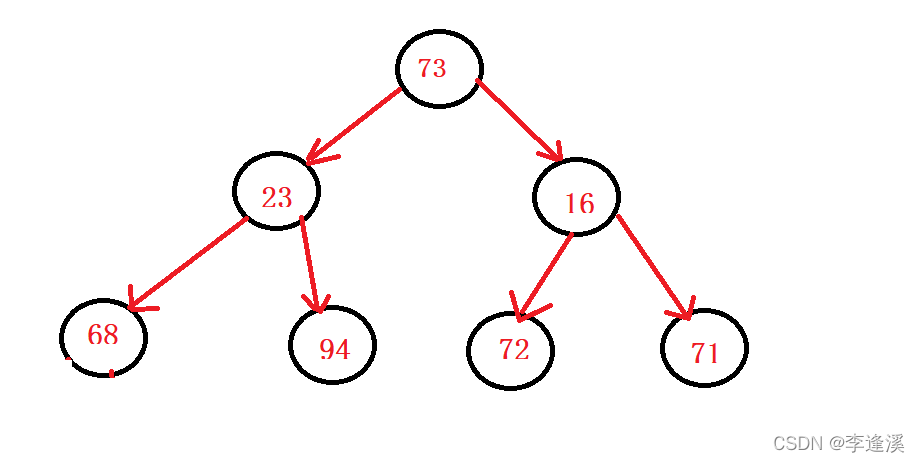
以下是一个小堆

 头删之后

 如何调整它，使得它还是一个小堆？

这里的思路是：向下调整算法，首先parent=73，然后选出它子节点最小的值，然后它们之间交换，交换之后，将子节点看作新的父亲节点，继续向下调整，直到父亲节点的左孩子不存在。

🌴参考代码：

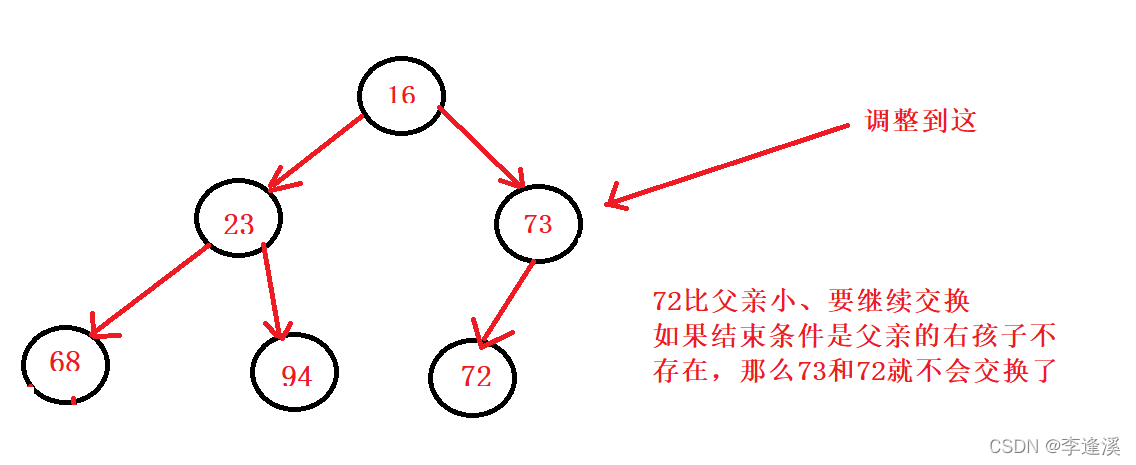
void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t parent = root;
	size_t child = parent * 2 + 1;
	while (child < size)
	{
		// 1、选出左右孩子中小的那个
		if (child + 1 < size && a[child+1] < a[child])
		{
			++child;
		}

		// 2、如果孩子小于父亲，则交换，并继续往下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

这里需要注意的是，为什么循环的结束条件不是右孩子不存在呢？

因为右孩子不存在时，也可能要进行交换。

比如：

 还需要注意的是左孩子存在右孩子不一定存在

if (a[child+1] > a[child])
{
	++child;
}

直接这样写a[child+1]可能会越界，因此要加上child + 1 < size，保证child + 1 <= size-1。

🌴参考代码：

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
    //将数组第一个元素和最后一个元素交换然后删除最后一个元素，达到头删的目的。
	Swap(&php->a[0], &php->a[php->size - 1]);
	--php->size;
    //向下调整算法
	AdjustDown(php->a, php->size, 0);
}

其他接口补充：

由于比较简单，理解起来不费劲，因此这里直接给出。

🌴参考代码：

bool HeapEmpty(HP* php)//判断堆是否为空
{
	assert(php);

	return php->size == 0;
}

size_t HeapSize(HP* php)//堆的元素个数
{
	assert(php);

	return php->size;
}

HPDataType HeapTop(HP* php)//取堆顶数据
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

三、堆排序

 堆排序：利用堆顶节点是整个数组的最大值或者最小值的特点，可以达到排序的目的。

比如我们要将1、5、2、4、8、6、10排成升序

可以将这几个元素依次入堆，使得这些数据变成小堆。

然后我们可以取堆的第一个元素，它是整个数组最小的元素，要排升序，那么我们就需要将它排在第一个位置，然后删除堆顶元素，由于我们的删除接口的作用是：删除堆顶元素，并保持堆还是小堆，那么我们调用删除接口之后，再取堆顶元素，将它排在第二个位置，依次继续下去，我们就能将这些数据排成升序了。

🌴参考代码：

void HeapSort(int* a, int size)
{
	HP hp;
	HeapInit(&hp);
    //建小堆
	for (int i = 0; i < size; ++i)
	{
		HeapPush(&hp, a[i]);
	}
    
    //不断取堆顶元素进行排序
	size_t j = 0;
	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}
    //销毁堆，防止内存泄露
	HeapDestroy(&hp);
}

这里的堆排序的空间复杂度是O（N），因为在堆区开辟了一个N个元素大小的堆空间。

堆排序看起来挺复杂的，那么它的时间复杂度是什么呢？

建小堆：0（N）

HeapPop（）一次执行的是：头删堆顶元素（O（1）），然后依次向下比较，比较的次数是高度次，因为是完全二叉树，比较的时间复杂度是O（logN）。

因此执行一次HeapPop的时间复杂度是O（logN）。

那么不断取堆顶元素进行排序，取了N个元素,调用了N次HeapPop（），时间复杂度是O（N*logN）。

总的时间复杂度是O（N）+O（N*logN），当N很大时，加的O（N）可以忽略。

实际时间复杂就是：O（N*logN）

空间复杂度：O（N）

那么堆排序的时间复杂度是O（N*logN）。

相比于冒泡排序的O（N*N）。

堆排序显然效率更高。

如果N等于100万，冒泡要执行1万亿次，而堆排序执行2千万次，效率可想而知！