多重网络中密集子图的新算法:S-core方法论
研究背景与意义
在复杂系统研究中,多重网络(Multilayer Networks,ML)已成为建模多维度互动的重要工具。这种模型在社会网络、生物系统和金融市场等领域具有广泛应用。例如,在社交网络分析中,个体间的互动可能同时涉及社交、专业和兴趣等多个层面。多重网络的概念为我们提供了一个更全面的框架,用以捕捉这些复杂的关系结构。
研究問題與挑戰
现有研究在将核心结构(core structures)概念扩展到多重网络时面临以下关键挑战:
- 约束条件过于严格:强制节点在预定义的子集层中满足度约束,可能导致忽视某些重要的密集结构。
- 计算复杂度高:现有算法通常需要指数级时间复杂度,难以应用于大规模实际网络。
- 层间信息整合困难:不同类型的关系在实际应用中可能具有不同的重要性,如何有效整合这些信息仍是一个开放问题。
创新方法:S-core
为解决上述问题,研究提出了S-core方法,这是一种新型的统一多重网络密集结构分析框架。S-core的核心思想是引入摘要函数S(.),将每个节点的多维度向量映射到低维空间,从而有效降低计算复杂度并避免过于严格的约束。
具体而言,给定一个d维阈值向量k,(k, S)-core被定义为一个最大子图,其中每个节点u在子图中的摘要度至少为k。这种定义方式提供了更大的灵活性,能够适应不同层的密度要求,同时保证了算法的高效性。
方法评估与应用价值
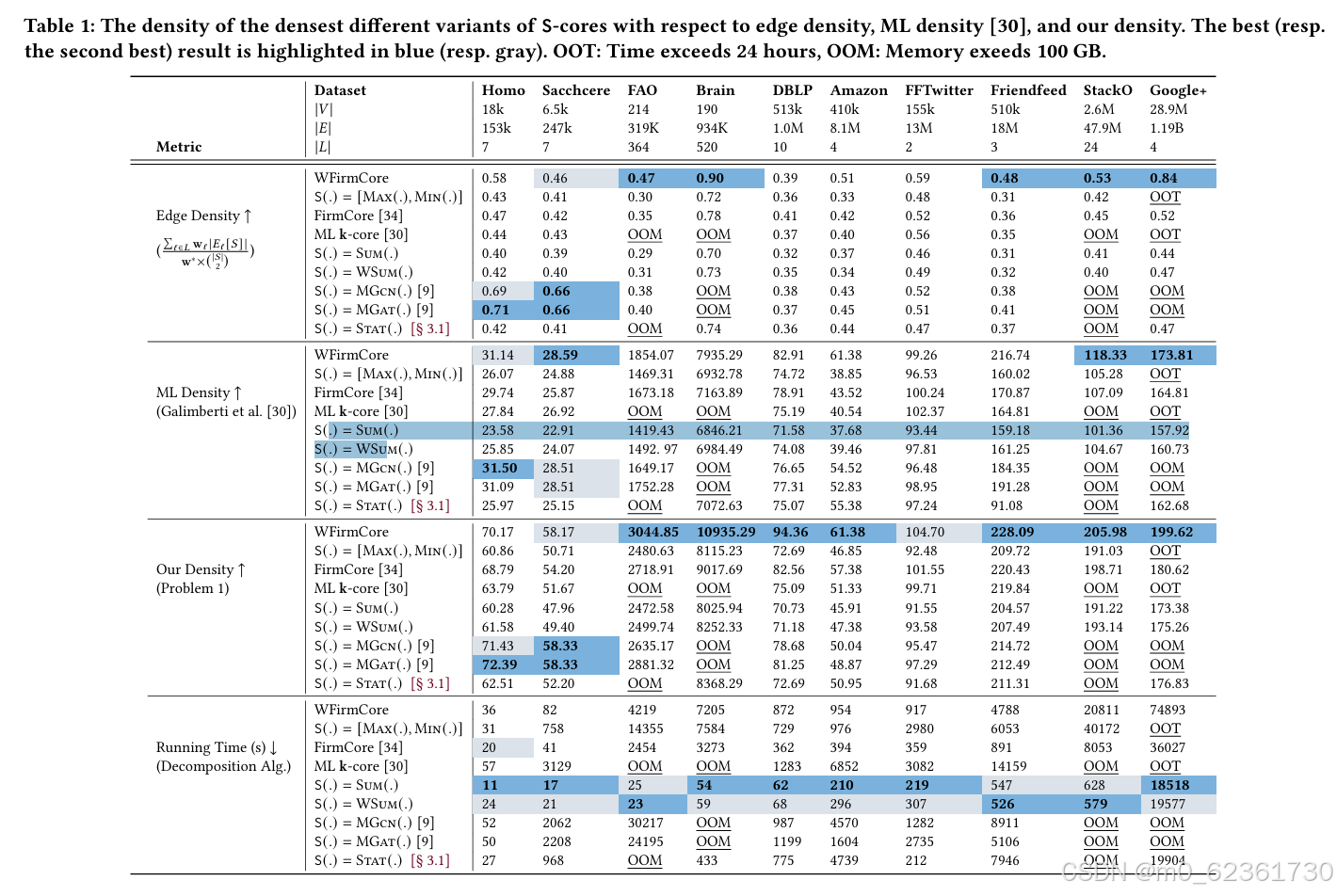
以下是不同的S-core变体在各种数据集上:
S-core方法的优势主要体现在以下几个方面:
- 统一性:能够统一并扩展现有的多种密集子图模型。
- 计算效率:通过摘要函数的引入,显著降低了计算复杂度。
- 模型灵活性:能够更准确地捕捉多重网络中的节点互动模式。
S-core在识别最密集子图和建模用户参与度方面表现卓越,不仅计算效率高,而且能够更精确地反映复杂网络中的结构特征。
密集子图算法比较分析
1. 传统单层网络密集子图算法
1.1 k-core分解
- 定义:k-core是图中的一个最大子图,其中每个顶点的度数至少为k。
- 优点:计算效率高,时间复杂度为O(m+n),其中m为边数,n为节点数。能够揭示网络的层次结构。
- 缺点:仅考虑度数,可能忽略其他重要的结构特征。
1.2 k-truss分解
- 定义:k-truss是图中的一个最大子图,其中每条边至少参与k-2个三角形。
- 优点:比k-core更能捕捉局部密集结构。能够发现更高阶的网络结构。
- 缺点:计算复杂度较高,通常为O(m^1.5)。
1.3 最大团(Maximum Clique)问题
- 定义:寻找图中最大的完全子图。
- 优点:提供了最严格的密集子图定义。
- 缺点:NP-hard问题,在大规模网络中计算代价极高。对噪声敏感,不适用于真实世界的稀疏网络。
2. 多重网络密集子图算法
2.1 向量阈值方法
- 定义:将k-core概念扩展到多重网络,要求每个节点在每一层都满足特定的度数阈值。
- 优点:直观地扩展了单层网络的概念。
- 缺点:计算复杂度高,通常需要指数时间。约束条件过于严格,可能错过某些重要的密集结构。
2.2 多重k-core分解
- 定义:在多重网络中寻找满足多维度约束的最大子图。
- 优点:能够捕捉多层网络中的复杂结构。
- 缺点:算法复杂度高,难以应用于大规模网络。对不同层的重要性处理不够灵活。
2.3 S-core方法(该研究提出)
- 定义:引入摘要函数S(.),将节点的多维度向量映射到低维空间,并在此基础上定义密集子图。
- 优点:计算效率高,避免了指数时间复杂度。提供了更灵活的密集结构定义,能够适应不同层的重要性。统一了多种现有的密集子图模型。
- 缺点:摘要函数的选择可能影响结果的质量。在某些特定应用中可能需要调整参数。
研究展望
S-core方法的提出为多重网络分析开辟了新的研究方向。未来的工作可以集中在以下几个方面:
- 摘要函数的优化:探索更多类型的摘要函数,以适应不同应用场景的需求。
- 动态网络分析:将S-core扩展到时变多重网络的分析中。
- 大规模并行算法:开发基于S-core的分布式算法,以应对超大规模网络的挑战。
- 跨学科应用:探索S-core在社会科学、生物信息学等领域的潜在应用。
总的来说,S-core方法为复杂网络分析提供了一个强大而灵活的工具,有望在多个领域产生重要影响。这项研究不仅推动了多重网络理论的发展,也为实际应用提供了新的分析视角和方法论支持。
论文地址: https://arxiv.org/abs/2406.13734