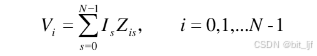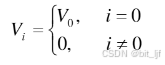matlab矩量法求解八木天线（五元）传输模型积分方程

一、实验原理

大部分代码实验原理与上一篇文章（矩量法求解线天线传输模型积分方程（含代码））相同，不同之处在于线天线单纯的只有一个激励源，而八木天线除去激励源，还有引向器与反射器产生的激励源。

因此为了清晰的分析八木天线，就要明白八木天线具体的工作原理以及具体的推导分析：

1.八木天线的结构

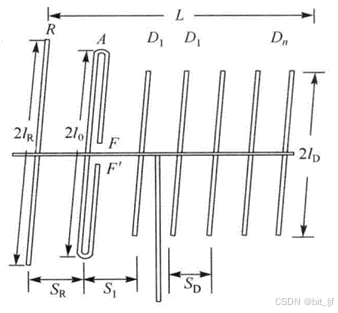
八木天线又称引向天线，由一个有源阵子（馈电元）和平行若干无源振子（寄生元）组成，如下图所示，其结构不仅包含一个反射振子，还有多个起引向器作用的无源振子。适当调节各振子的长度与间距，可改变无源振子上感应电流的相位和振幅，进而活得良好的端射方向图和较高的增益。

2.八木天线的工作原理

八木天线的引向器略短于二分之一波长，主振子约等于二分之一波长，反相器略长于二分之一波长，间距略等于四分之一波长。此时，引向器对感应信号呈现容性，电流超前电压90°相位；主振子产生的电磁波向引向器方向辐射时，辐射信号经过四分之一波长的路程使其相位与引向器上产生的相位差抵消，两者相位相同，信号叠加得到加强。反射器略长于二分之一波长，呈感性，电流滞后电压90°相位，主振子辐射到反相器的过程中又滞后90°，总共180°的相位差，信号相抵消。一个方向加强一个方向削弱，使八木天线有很强的方向性。

3.利用感应电动势法分析八木天线

将八木天线看作电流振幅和相位及间距都不均匀的端射式直线阵，利用耦合振子理论得到耦合方程近似计算各振子上的电流分布

耦合方程如下：

式中：

表示归算于电流波腹的第i根振子与第s根振子间的互阻抗。表示归算于电流波腹的第i根振子的自阻抗。

二、实验代码及其详解

与之前文章相似，不同之处有两点，第一是匹配点坐标从原来的只需一个x轴变为x、y轴，其次是在计算出Z矩阵之后，要对其较远两端的互阻抗处理

1.基础参数设置

a=0.001;   %天线半径a
f = 3e8;
lambda = 3e8/f;
k=2*pi/lambda;
h1=0.6;  
h2=0.5; 
h3=0.45; 
h4=0.45;
h5=0.45;
d=0.25; 
N1=59;   %网格数
N2=59; 
N3=59; 
N4=59;
N5=59;
delta_h1 = h1/(N1+1);   %网格的长度
delta_h2 = h2/(N2+1); 
delta_h3 = h3/(N3+1); 
delta_h4 = h4/(N4+1);
delta_h5 = h5/(N5+1);

2.分割线天线并初始化匹配点、端点坐标

h1_zm_y=-h1/2:delta_h1:h1/2;   %zm_y中是配置点的纵坐标
h1_zm_yy=h1_zm_y(2:N1+1);   %zm_yy中是除端点外配置点的纵坐标

h2_zm_y=-h2/2:delta_h2:h2/2; 
h2_zm_yy=h2_zm_y(2:N2+1); 

h3_zm_y=-h3/2:delta_h3:h3/2; 
h3_zm_yy=h3_zm_y(2:N3+1);

h4_zm_y=-h4/2:delta_h4:h4/2;
h4_zm_yy=h4_zm_y(2:N4+1);

h5_zm_y=-h5/2:delta_h5:h5/2;
h5_zm_yy=h5_zm_y(2:N5+1);
N = N1+N2+N3+N4+N5;   %总网格数

在下面的代码片段中，建立一个包含引向器、有源阵子、反射器的结构矩阵，设立匹配点的高度坐标从一一被赋值，而积分区域与分别为相近两匹配点之间的中点，其中y坐标从左向右依次被赋值，由此得到了匹配点具体坐标，其中A矩阵存储网格各段端点坐标，B矩阵中存储的是匹配点的坐标；

for i=1:N 
        if i<=N1 
            A(i).y=-d; 
            A(i).z=h1_zm_yy(i); 
        elseif (i<=N1+N2)&&(i>N1) 
            A(i).y=0; 
            A(i).z=h2_zm_yy(i-N1); 
        elseif(i<=N1+N2+N3)&&(i>N1+N2)
            A(i).y=d; 
            A(i).z=h3_zm_yy(i-N1-N2); 
        elseif (i<=N1+N2+N3+N4)&&(i>N1+N2+N3)
            A(i).y=2*d;
            A(i).z=h4_zm_yy(i-N1-N2-N3);
        else
            A(i).y=3*d;
            A(i).z=h5_zm_yy(i-N1-N2-N3-N4);
        end 
end 
for i=1:N+10 
        if i<=N1+2 
            B(i).y=-d; 
            B(i).z=h1_zm_y(i); 
        elseif (i<=N1+N2+4)&&(i>N1+2) 
            B(i).y=0; 
            B(i).z=h2_zm_y(i-N1-2); 
        elseif (i<=N1+N2+N3+6)&&(i>N1+N2+4)
            B(i).y=d; 
            B(i).z=h3_zm_y(i-N1-N2-4); 
        elseif (i<=N1+N2+N3+N4+8)&&(i>N1+N2+N3+6)
            B(i).y=2*d;
            B(i).z=h4_zm_y(i-N1-N2-N3-6);
        else
            B(i).y=3*d;
            B(i).z=h5_zm_y(i-N1-N2-N3-N4-8);
        end 
end

3.计算V、Z矩阵元素值

delta_h=[delta_h1,delta_h2,delta_h3,delta_h4,delta_h5];
for i=1:5
    znn_1=1/(4.*pi).*log((sqrt(delta_h(i).*delta_h(i)+4.*a.*a)+delta_h(i))/(sqrt(delta_h(i).*delta_h(i)+4.*a.*a)-delta_h(i)));
    znn_2=-1j.*k.*delta_h(i)/(4.*pi);
    znn_3=1/(8.*pi).*(delta_h(i)/2.*sqrt(4.*a.*a+delta_h(i).*delta_h(i))+a.*a.*log((sqrt(delta_h(i).*delta_h(i)+4.*a.*a)+delta_h(i))/(sqrt(delta_h(i).*delta_h(i)+4.*a.*a)-delta_h(i))));
    znn(i)=znn_1+znn_2+znn_3;
end

将输入阻抗矩阵的对角线元素的值一一算出，即m=n时出现的奇异点按照泰勒展开进行积分；

依次在矩阵内部划分区域，当在相同的y坐标时，计算公式按照线天线计算即可，若不在相同的y坐标，则需要将原来的转变为

for i=1:N+10 
    if i<=N1+2 
        flag1=1; 
        V0=0; %表面电流
    elseif i<=N1+N2 +4
        flag1=2; 
        V0=1; 
    elseif i<=N1+N2+N3+6
        flag1=3; 
        V0=0; 
    elseif i<=N1+N2+N3+N4+8
        flag1=4;
        V0=0;
    else
        flag1=5;
        V0=0;
    end 
    for j=1:N+10 
        if j<=N1+2 
            flag2=1; 
            dh=delta_h1; 
            const=znn(1);
        elseif j<=N1+N2+4 
            flag2=2; 
            dh=delta_h2;
            const=znn(2);
        elseif j<=N1+N2+N3+6 
            flag2=3; 
            dh=delta_h3; 
            const=znn(3);
        elseif j<=N1+N2+N3+N4+8
            flag2=4;
            dh=delta_h4;
            const=znn(4);
        else
            flag2=5;
            dh=delta_h5;
            const=znn(5);
        end
        if(j==1||j==N1+3||j==N1+N2+5||j==N1+N2+N3+7||j==N1+N2+N3+N4+9)
            Z(i,j)=-1.*cos(k.*B(i).z);
        else 
            if i==j 
                Z(i,j)=const; 
            else 
                if flag1==flag2 
                    R_ij=sqrt((B(i).z-B(j).z)^2+a^2); 
                else 
                    R_ij=sqrt((B(i).y-B(j).y)^2+(B(i).z-B(j).z)^2); 
                end 
                    Z(i,j)=exp(-1j*k*R_ij)/(4*pi*R_ij)*dh; 
            end 
        end
    end 
    V(i,1)=V0*(-1j)*sin(k*(abs(B(i).z)))/(2*120*pi);   %计算矩阵V
end

处理Z矩阵，对于段的辐射，在后认为是0，同理段之外也是0，依次设定，将Z矩阵设定成功后解方程即可。

for i=1:N1+2
    Z(i,1)=0;
end
for i=N1+N2+5:N+10
    Z(i,1)=0;
end

for i=1:N1+N2+4
    Z(i,N1+3)=0;
end
for i=N1+N2+N3+7:N+10
    Z(i,N1+3)=0;
end

for i=N1+3:N+10
    Z(i,N1+N2+5)=0;
end

for i=1:N1+N2+N3+N4+8
    Z(i,N1+N2+N3+7)=0;
end

for i=1:N1+N2+N3+6
    Z(i,N1+N2+N3+N4+9)=0;
end
for i=N1+N2+N3+N4+9:N+10
    Z(i,N1+N2+N3+N4+9)=0;
end

4.求解获得I矩阵以及结果输出

IA=linsolve(Z,V);   %求解矩阵方程，得到电流I
IA=[0;IA(2:N1+2);0;IA(N1+4:N1+N2+4);0;IA(N1+N2+6:N1+N2+N3+6);0;IA(N1+N2+N3+8:N1+N2+N3+N4+8);0;IA(N1+N2+N3+N4+10:N+10);0];

%绘制电流曲线
figure(1) 
plot(abs(IA),'m:','linewidth',2) 
xlabel('位置z/m'),ylabel('电流I幅值/A');
title('八木天线的电流分布');
grid on 
Z_V=N1+N2+N3+N4+(N5+1)/2; 
Z_in=1/IA(Z_V); 

theta=0:pi/100:2*pi;
phi=pi/2; 
for i=1:length(theta) 
    F(i)=0; 
    for j=1:N+10
        if j<=N1+2 
            dh=delta_h1; 
        elseif j>N1+2 && j<=N1+N2+4 
            dh=delta_h2; 
        elseif j>N1+N2+4 && j<=N1+N2+N3+6 
            dh=delta_h3; 
        elseif j>N1+N2+N3+6 && j<=N1+N2+N3+N4+8
            dh=delta_h4;
        else
            dh=delta_h5;
        end 
    F(i)=F(i)+IA(j)*exp(1j*k*(B(j).y*sin(theta(i))*sin(phi)+B(j).z*cos(theta(i))))*dh*(-sin(theta(i))); 
    end 
end 
F=abs(F); 
F1=F/max(F); 
figure(2) 
polarplot(theta,F1);   %绘制二维方向图
title('八木天线的二维方向图');
gain = 20*log10(F(51)/F(151))    %计算增益dB