一、实验目的
1. 熟悉回溯法的基本思想;
2. 使用回溯法分析、解决问题;
3. 实现算法。
二、实验内容
- 分析4皇后问题的解空间树
- 实现使用回溯法解决4皇后问题
三、问题分析
4皇后问题指在4×4的棋盘上放置彼此不受攻击的 4 个皇后,皇后可以攻击与之在同一行、同一列、同一斜线上的棋子。设计算法在4×4的棋盘上放置4个皇后,使其彼此不受攻击,n皇后问题一般采用回溯法来解决。
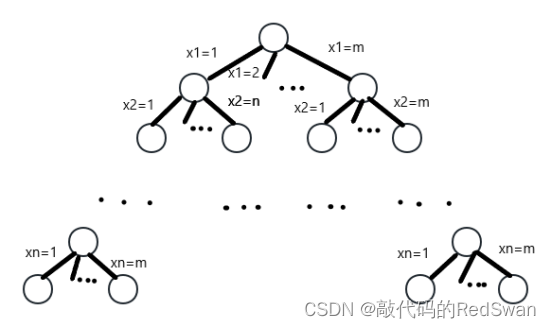
n皇后问题的解空间树如下:
四、算法描述
采用回溯算法,从根开始,以深度优先搜索的方式进行搜索。根结点是活结点,并且是当前的扩展结点。在搜索过程中,当前的扩展结点沿纵深方向移向一个新结点,判断该新结点是否满足隐约束。如果满足,则新结点成为活结点,并且成为当前的扩展结点,继续深一层的搜索;如果不满足,则换到该新结点的兄弟结点继续搜索:如果新结点没有兄弟结点,或其兄弟结点已全部搜索完毕,则扩展结点成为死结点,搜索回溯到其父结点处继续进行。搜索过程直到找到问题的根结点变成死结点为止。
1.约束函数
在第t行放置第t个皇后时,第t个皇后与前t-1个已放置好的皇后不能在同一列或同一斜线。如果有一个成立,则第t个皇后不可以放置在该位置。
x[t]= =x[j]表示第t个皇后和第j个皇后位置在同一列,t-j=fabs(x[t]-x[j])表示第t个皇后和第j个皇后位置在同一斜线。
2.按约束条件搜索求解
t表示当前扩展结点在第t层。如果t> n,表示已经到达叶子结点,记录最优值和最优解,返回。否则,分别判断 n (i=l,...,n)个分支,x[t]=i:判断每个分支是否满足约束条件,如果满足则进入下一层 Backtrack(t+1);如果不满足则检查下一个分支。
五、源代码
#include <iostream>
#include <cmath>
#define M 105
using namespace std;
int n;//表示n个皇后
int cnt;//n皇后问题的解法个数
int x[M];//x[i]表示第i个皇后放置在第i行第x[i]列
bool Place(int t)//约束函数
{
bool check=true;
for (int j=1;j<t;j++)
{
if (x[t]==x[j] || t-j==fabs(x[t]-x[j]))//判断列、对角线是否冲突
{
check=false;
break;
}
}
return check;
}
void Backtrack(int t)//回溯法解决n皇后问题
{
if (t>n)//如果当前位置为n,则表示已经找到了问题的一个解
{
cnt++;
for (int i=1;i<=n;i++)//打印选择的路径
{
cout<<x[i]<<" ";
}
cout<<endl;
}
else for (int i=1;i<=n;i++)
{
x[t]=i;
if (Place(t))
Backtrack(t+1);//如果不冲突则继续进行下一行的搜索
}
}
int main()
{
cout<<"请输入皇后的个数:";
cin>>n;
cnt=0;
Backtrack(1);//1表示从棋盘第一个位置开始
cout<<n<<"皇后问题的解法有"<<cnt<<"种";
return 0;
}六、运行结果
请输入皇后的个数:4
2 4 1 3
3 1 4 2
4皇后问题的解法有2种