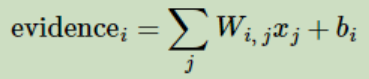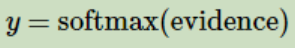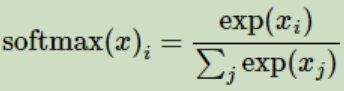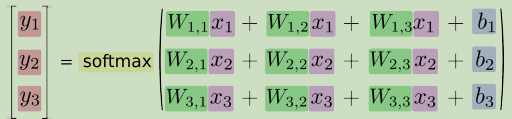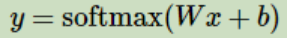Tensorflow手写数字识别

一.MNIST数据集

当我们开始学习编程的时候，第一件事往往是学习打印"Hello World"。就好比编程入门有Hello World，机器学习入门有MNIST。
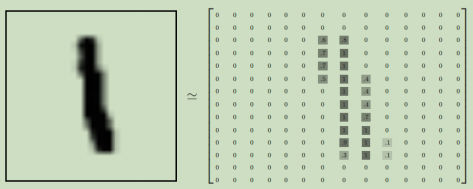
MNIST是一个入门级的计算机视觉数据集，它包含各种手写数字图片：
在这里插入图片描述
它也包含每一张图片对应的标签，告诉我们这个是数字几。比如，上面这四张图片的标签分别是5，0，4，1。

为了便于下载MNIST数据集，执行下面的python代码【需要提前安装好tensorflow】可以将该数据集下载到本地：

from tensorflow.examples.tutorials.mnist import input_data

# mn.SOURCE_URL = "http://yann.lecun.com/exdb/mnist/"
my_mnist = input_data.read_data_sets("C:/Users/Administrator/MNIST_data_bak/", one_hot=True)

下载下来的数据集被分为两部分：60000行的训练数据集【mnist.train】和10000行的测试数据集【mnist.test】。这样的切分很重要，在机器学习模型设计时必须有一个单独的测试数据集不是用于训练模型，而是用于评估模型的性能，从而更加容易地把设计的模型推广到其它数据集上【泛化能力】。
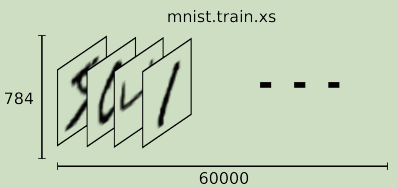
每一个MNIST数据单元由两部分组成：一张包含手写数字的图片和一个对应的标签。我们把这些图片设为xs，把这些标签设为ys。训练数据集和测试数据集都包含xs和ys，比如训练数据集的图片是mnist.train.images，训练数据集的标签是mnist.train.labels。
每张图片包含2828个像素点。我们可以用一个数字数组来表示这张图片：

我们把这个数组展开成一个向量，长度是2828=784。如何展开这个数组【数字间的顺序】并不重要，只需保证各个图片的展开方式相同。从这个角度来看，MNIST数据集的图片就是在784维向量空间里面里面的点，并且拥有比较复杂的结构【此类数据的可视化是计算密集型】。
展开图片的数字数组会丢失图片的二维结构信息。这显然是不理想的，最优秀的计算机视觉方法会挖掘并利用这些结构信息。但在此处我们忽略这些结构，所介绍的简单数学模型，softmax回归【softmax regression】不会利用这些结构信息。
因此，在MNIST训练数据集中，mnist.train.images是一个形状为[60000, 784]的张量，第一个维度数字用来索引图片，第二个维度数字用来索引每张图片中的像素点。在此张量里的每一个元素，都表示某张图片里的某个像素的强度值，介于0~1之间。
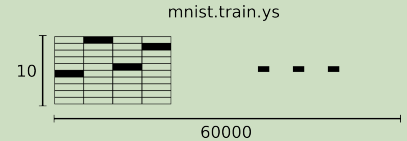
在这里插入图片描述
相对应的MNIST数据集的标签介于0~9之间的数字，用来描述给定图片里表示的数字。为了便于分析，我们把标签数据转换为one-hot编码向量。一个one-hot向量除了某一位的数字是1之外，其余各个维度数字都是0。因此，数字n将表示成一个只有在第n维度数字为1的10维向量。比如，标签0将表示为：[1,0,0,0,0,0,0,0,0,0]。因此，mnist.train.labels将是一个[60000,10]的数字矩阵。
在这里插入图片描述

二.Softmax回归介绍

我们知道MNIST的每一张图片都表示一个数字，从0到9.我们希望得到给定图片代表每个数字的概率。比如说，我们的模型可能推测一张包含9的图片代表数字9的概率是80%，但是判断它是8的概率是5%【8和9比较接近】，然后给予它代表其他数字更小的概率值。
这是一个使用softmax回归模型的经典案例。softmax模型可以用来给不同的对象分配概率。即使使用更加复杂的模型时，最后一步也需要用softmax来分配概率。
softmax回归模型分两步：
1.为了得到一张给定图片属于某个特定数字的证据，我们对图片像素值进行加权求和。如果这个像素具有很强的证据说明这张图片不属于该数字，那么相应的权值为负数，否则权值为正值。
下面的图片显示了一个模型学习到的图片上每个像素对于特定数字的权值。红色代表负数权值，蓝色代表正数权值。
在这里插入图片描述
我们也需要加入一个额外的偏置量【bias】，因为输入往往会带有一些无关的干扰量。因此对于给定的输入图片x它代表的是数字i的证据可以表示为：

其中bi代表数字i的偏置量，j代表给定图片x的像素索引用于像素求和。然后用softmax函数可以把这些证据转换成概率y：
在这里插入图片描述
这里的softmax可以看成是一个激励【activation】函数或者链接【link】函数，把我们定义的线性函数的输出转换成我们想要的格式，也就是关于10个数字的概率分布。因此，给定一张图片，它对于每一个数字的吻合度可以被softmax函数转换成为一个概率值。softmax函数可以定义为：
在这里插入图片描述
展开等式右边的子式，可以得到：

但是更多的时候把softmax模型函数定义为前一种形式：把输入值当成幂指数求值，再正则化这些结果值。这个幂运算表示，更大的证据对应更大的假设模型【hypothesis】里面的乘数权重值。反之，拥有更少的证据意味着在假设模型里面拥有更小的乘数系数。假设模型里的权值不可以是0或者负值。Softmax会正则化这些权重值，使它们的总和等于1，以此构造一个有效的概率分布。
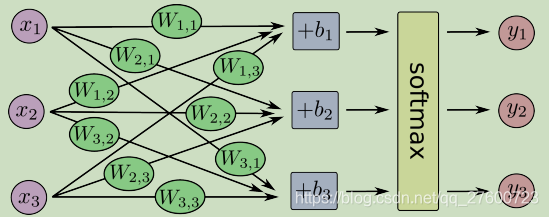
对于softmax回归模型可以用下面的图解释，对于输入的xs加权求和，再分别加上一个偏置量，最后再输入到softmax函数中：
在这里插入图片描述
如果把它写成一个等式，我们可以得到：

我们也可以用向量表示这个计算过程：用矩阵乘法和向量相加。这有助于提高计算效率。

更近一步，可以写成更加紧凑的方式：

三.实现回归模型

为了用python实现高效的数值计算，我们通常会使用函数库，比如NumPy，会把类似矩阵乘法这样复杂的运算使用其他外部语言实现。不幸的是，从外部计算切换回Python的每一个操作，仍然是一个很大的开销。如果你是使用的GPU来进行外部计算，这样的开销会更大。用分布式的计算方式，也会花费更多的资源用来传输数据。
TensorFlow也会把复杂的计算放在python之外完成，但是为了避免前面说的那些开销，它做了进一步的完善。TensorFlow不单独运行单一的复杂计算，而是让我们可以先用图描述一系列可交互的计算操作，然后全部一起在Python之外运行。
使用TensorfFlow之前，首先导入它：

import tensorflow as tf

我们通过操作符号变量来描述这些可交互的操作单元，可以用下面的方式创建一个：

x = tf.placeholder("float", [None, 784])

x不是一个特定的值，而是一个占位符placeholder，我们在TensorFlow运行计算时输入这个值。我们希望能够输入任意数量的MNIST图像，每一张图展开成784维的向量。用2维的浮点数张量来表示这些图，这个张量的形状是【None, 784】。
备注：None表示此张量的第一个维度可以是任何长度的！
我们的模型也需要权重值和偏置量，当然我们可以把它们当做是另外的输入【使用占位符】，但TensorFlow有一个更好的方法来表示它们：Variable。一个Variable代表一个可修改的张量，存在在TensorFlow的用于描述交互式操作的图中。它们可以用于计算输入值，也可以在计算中被修改。对于各种机器学习应用，一般都会有模型参数，可以用Variable表示。