GAN+文本生成：让文本以假乱真

转载：https://zhuanlan.zhihu.com/p/36880287?utm_source=wechat_timeline&utm_medium=social&utm_oi=623434717970698240&from=timeline&isappinstalled=0&wechatShare=1

论文一、《Generative Adversarial Nets》NIPS 2014

1、模型简述

这篇论文是最早提出 GAN 的文章，作者 Ian J. Goodfellow 提出了一种新的对抗过程来评价生成模型的效果。GAN 主要分为两部分：生成模型和判别模型。生成模型的作用是模拟真实数据的分布，判别模型的作用是判断一个样本是真实的样本还是生成的样本，GAN 的目标是训练一个生成模型完美的拟合真实数据分布使得判别模型无法区分。

生成模型和判别模型之间的交互可以类比为这样一个场景：生成模型是一个生产假币的伪造者，他的任务就是要生成假币然后使用假币而不被发现，判别模型则是一个警察，他的任务则是识别出那些假币，两者之间的较量使得伪造者不断提升制造假币的能力，警察不断提升识别假币的能力，最终警察无法区分伪造者生产的假币和真实的货币。

2、数学表示

真实数据分布： $x\sim p_{data}(x)$

生成模型： $G(z;\theta_g)$ ，其中是噪声输入，满足分布 $z\sim p_z(z)$ ， $\theta_g$ 是参数，最终生成的样本满足分布 p_g ，生成模型的目标是要尽量使得 p_g 拟合 $p_{data}$ 。

判别模型： $D(x;\theta_{d})$ ，其中是输入的样本， $\theta_d$ 是参数，最终输出来自 $p_{data}$ 而不是 p_g 的概率。

最后的训练目标为：

$\min \limits_{G} \max \limits_{D} V(D,G)=\mathbb{E}_{x\sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_z(z)}[\log (1-D(G(z))]$

解释一下：

对于生成模型，它希望判别真实数据的概率低，判别生成数据 G(z) 的概率高，所以 V(D,G) 的值小；

对于判别模型，它希望判别真实数据的概率高，判别生成数据 G(z) 的概率低，所以 V(D,G) 的值大。

3、算法

这是训练 GAN 的算法，在训练时，并不是生成模型和判别模型交替训练，而是训练次判别模型同时训练1次生成模型。在训练早期，判别模型能够轻松否定 G(z) ， D(G(z)) 值很小， $\log (1-D(G(z)))$ 接近饱和，因此对于而言，我们不试图优化 $\min \limits_G \log(1-D(G(z)))$ ，而是 $\max \limits_G \log(D(G(z)))$ 。

训练的最后将达到一个全局最优条件： $p_g=p_{data}=0.5$ ，同时若固定， D_G^*(x) 收敛为 $\frac {p_{data}(x)}{p_{data}(x)+p_g(x)}$ 。

证明：
若固定，则训练目标为 $\max \limits_{D} V(G,D)$ 。
$\begin{align} V(D,G) &= \mathbb{E}_{x\sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_z(z)}[\log (1-D(G(z))] \\ &= \int_{x} p_{data}(x)\log(D(x))dx + \int_{z} p_z(z) \log(1-D(G(z)))dz \\ &= \int_{x} p_{data}(x)\log(D(x))dx + p_g(x) \log(1-D(G(x)))dx \end{align} \\$
对于区间 $(a,b) \in \mathbb{R}^2 \backslash \{0,0\}$ 来说，函数 $x\rightarrow a\log(x) + b\log(1-x)$ 的最优解在 $\frac {a}{a+b}$ 处取得，即 $D^*_{G}(x)= \frac {p_{data}(x)}{p_{data}(x)+p_g(x)}$ 。
$\begin{align} C(G) &= \max \limits_{D}V(G,D) \\ &= \mathbb{E}_{x\sim p_{data}} \log[D_G^*(x)] + \mathbb{E}_{z\sim p_z}\log[1-D_G^*(G(z))] \\ &= \mathbb{E}_{x\sim p_{data}} \log[D_G^*(x)] + \mathbb{E}_{x\sim p_g}\log[1-D_G^*(x)] \\ &= \mathbb{E}_{x\sim p_{data}} \log \frac {p_{data}(x)}{p_{data}(x)+p_g(x)} + \mathbb{E}_{x\sim p_g} \log \frac {p_g(x)}{p_{data}(x)+p_g(x)} \end{align} \\$
那么最终训练目标是最小化，即 $\min \limits_{G}C(G)$ ，下证当且仅当 $p_g=p_{data}$ ，此时最小值 $C(G)=-\log4$ 。
KL-散度：衡量两个概率分布之间的差异情况。 $D(P||Q)=\sum_{x \in X}{\log \frac {P(x)}{Q(x)}}$
那么
$\begin{align} \mathbb{E}_{x\sim p_{data}} \log \frac {p_{data}(x)}{p_{data}(x)+p_g(x)} &= \int_{x} p_{data}(x) \log \frac {p_{data}(x)}{p_{data}(x)+p_g(x)} \\ &= \int_{x} p_{data}(x) \log [\frac {p_{data}(x)}{\frac {p_{data}(x)+p_g(x)}{2}} * \frac {1}{2}] \\ &= KL(p_{data}||\frac {p_{data}+p_g}{2}) + \int_{x}p_{data}(x) \log \frac {1}{2} \\ &= KL(p_{data}||\frac {p_{data}+p_g}{2}) + \log \frac {1}{2} \end{align} \\$
同理， $\begin{align} \mathbb{E}_{x\sim p_g} \log \frac {p_g(x)}{p_{data}(x)+p_g(x)} = KL(p_g||\frac {p_{data}+p_g}{2}) + \log \frac {1}{2} \end{align}$

JS-散度：衡量两个概率分布之间的相似度。 $JS(P||Q)=\frac {1}{2}KL(P||\frac {P+Q}{2})+\frac {1}{2}KL(Q||\frac {P+Q}{2})$

因此
$\begin{align} C(G) &=-\log4 + KL(p_{data}||\frac {p_{data}+p_g}{2})+KL(p_g||\frac {p_{data}+p_g}{2}) \\ &= -\log4+2 \cdot JS(p_{data}||p_g) \end{align} \\$
JS-散度总是大于等于0，当且仅当时，。所以
$C(G)-(-\log4)=2 \cdot JS(p_{data}||p_g) \geq 0$ ，最小值是 $-\log4$ ，当且仅当 $p_{data}=p_g$ 。

论文二、《GANs for Sequences of Discrete Elements with the Gumbel-softmax Distribution》 2016

1、写作动机

虽然 GAN 在计算机视觉领域取得巨大的成功，但对于离散型数据的序列却捉襟见肘。原因在于，从离散对象的分布中采样这一过程是不可导的，因此参数难以更新。作者认为，这一问题可以通过 Gumbel-softmax 分布来避免，Gumbel-softmax 分布是对基于 softmax 函数的多项式分布的一个连续逼近。

Gumbel分布是一种极值型分布。举例说明，假设每次测量心率值为一个随机变量（服从某种指数型分布，如正态分布），每天测量10次并取最大的心率作为当天的心率测量值。显然，每天记录的心率值也是一个随机变量，并且它的概率分布即为 Gumbel 分布。

2、Gumbel-softmax 分布

对于一个 d 维向量和一个 d 维 one-hot 向量，softmax 函数可以参数化表示上的多项分布。是一个 d 维向量，表示上的多项分布，其中 p_i=p(y_i=1),i=1,...,d ，所以

$p=\text{softmax}(h) \tag{1} \\$

$[\text{softmax}(h)]_i=\frac {\exp(h_i)}{\sum_{j=1}^{d}{\exp(h_j)}},i=1,...,d \tag{2} \\$

式（1）按照向量中的概率对进行多项分布的采样等价于：

$y=\text{one_hot}(\mathop{\arg\max} \limits_{i}(h_i+g_i)) \tag{3} \\$

这里的 g_i 相互独立且符合 Gumbel 分布，可以证明， $\mathop{\arg\max}(h_i+g_i)$ 的分布等于由 softmax 函数计算的概率分布。

但是，式（3）对向量的梯度等于0，因为 $\text{one_hot}(\mathop{\arg\max}(\cdot))$ 操作是不可导的。作者提出了一种基于 softmax 转换的可微函数来逼近式（3）:

$y=\text{softmax}(\frac {1}{\tau (h+g)}) \tag{4} \\$

这里的 $\tau$ 是一个控制 softmax 函数 soft 程度的参数，当 $\tau\rightarrow0$ ，式（4）和式（3）生成的样本接近一样，当 $\tau\rightarrow \infty$ ，式（4）生成的样本满足均匀分布，当 $\tau$ 大于0且有限时，式（4）生成的样本比较平滑而且对可导。因此，这里的式（4）所代表的的概率分布就称为 Gumbel-softmax 分布，GAN 在离散型数据上的训练可通过式（4）进行， $\tau$ 最开始的值较大，慢慢接近于0 。

3、模型算法

原始的生成模型是对隐藏状态 h_i 做 softmax 操作取最大值对应的单词，但因为从 softmax 分布采样输出这一过程是不可导的，所以训练中对隐藏状态 h_i 使用 Gumbel-softmax 分布进行采样输出，最终，生成模型和判别模型的参数都可以通过基于梯度的算法进行更新。

论文三、《Generating Text via Adversarial Training》NIPS 2016 Workshop

1、写作动机

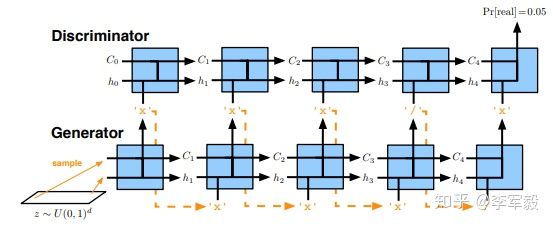
本篇论文同样是为了解决 GAN 模型中离散输出的问题。作者以 LSTM 作为 GAN 的生成器，以 CNN 作为 GAN 的判别器，并使用光滑近似（smooth approximation）的思想逼近生成器 LSTM 的输出，从而解决离散导致的梯度不可导问题。与原始 GAN 模型的目标函数不同，作者的优化函数采用的是 feature matching 的方法，并使用了多种训练手段来改善 GAN 模型的收敛性。

2、TextGAN 模型定义

语料集： $S=\{s_1, \cdots ,s_n \}$ ， s_i 表示第个句子，表示句子个数。

句子： $s=\{w^t\}_{t=1}^m$ ， w^t 表示句子的第个单词。每一个单词 w^t 都映射为一个 k 维词向量 x_t=W_e[w^t] ，其中 $W_e \in \mathbb{R}^{k\times V}$ 是在训练过程中逐渐学习的词嵌入矩阵，是词典的大小，符号 [v] 表示单词在词典中对应的索引值。

CNN discriminator:

一个长度为（长度不足则补齐）的句子可以表示成一个矩阵 $X \in \mathbb{R}^{k\times T}$ ，它的每一列由句子中单词的词向量组成，例如第列是单词 x_t 的词向量。

抽取句子的一个特征需要对句子进行一次卷积操作和池化操作。

卷积核 filter： $W_c\in \mathbb{R}^{k\times h}$ ，对句子中 h 大小窗口内的连续单词做卷积： c=f(X * W_c +b) ，其中 $f(\cdot)$ 是一个非线性激活函数，是卷积操作，最终得到一个 feature map ，然后对 feature map 做最大池化操作， $\hat{c}=\max\{c\}$ 作为这次操作的最终特征。

最大池化的目的是为了获取最重要的特征（对应重要的单词位置），过滤掉信息量少的单词。

在实验中，作者使用了多个卷积核 filter 以及多种窗口大小 h 。每一个卷积核都可以看做是一个语言特征的提取器，它能够识别提取 h-gram 的特征。假设我们有 m 种窗口大小， d 个卷积核，最终我们可以得到一个 md 维的特征。在这个 m*d 维的特征之上，应用一个 softmax 层映射为输出 $D(X)\in [0,1]$ ，表示句子来自真实数据的概率。

LSTM generator:

生成器将一个输入噪声映射为一个句子 $\tilde{s}$ 。生成概率为：

$p(\tilde{s}|z)=p(w^1|z)\prod_{t=2}^{T}p(w^t|w^{<t},z) \\$

$p(w^1|z)=\arg\max(Vh_1) \\$

$h_1=\tanh(Cz) \\$

之后的所有单词则按顺序使用 LSTM 计算得出，直至遇到结束标志符。

$p(w^t|w^{<t},z)=\arg\max(Vh_t) \\$

$h_t=\text{LSTM}(y_{t-1},h_{t-1},z) \\$

$y_{t-1}=W_e[w^{t-1}] \tag{*}\\$

需要注意的是，噪声作为额外的 LSTM 输入指导句子的生成。模型框架如下：

3、训练方法

本篇论文的目标函数和原始 GAN 有所不同，文中采用了 feature matching 的方法。迭代优化过程包含以下两个步骤：

$\begin{align} \text{minimizing:}&\ L_D=-\mathbb{E}_{s\sim S}\log D(s)-\mathbb{E}_{z\sim p_z(z)}\log [1-D(G(z))] \\ \text{minimizing:}&\ L_G=\text{tr}(\Sigma^{-1}_s\Sigma_r+\Sigma^{-1}_r\Sigma_s)+(\mu_s-\mu_r)^{\mathrm{T}}(\Sigma^{-1}_s+\Sigma^{-1}_r)(\mu_s-\mu_r) \\ \end{align}$

其中 $\Sigma_s$ 和 $\Sigma_r$ 分别表示生成句子特征向量 f_s 和真实句子特征向量 f_r 的协方差矩阵， $\mu_s$ 和 $\mu_r$ 则分别表示 f_s 和 f_r 的平均值。 $\Sigma_s$ , $\Sigma_r$ , $\mu_s$ 和 $\mu_r$ 都是通过经验设置。通过设置 $\Sigma_s=\Sigma_r=\text{I}$ ，生成器的优化则变成了 feature matching 方法。第二个损失 L_G 是两个多元正态分布 $N(\mu_r,\Sigma_r)$ 和 $N(\mu_s,\Sigma_s)$ 的 JS-散度。论文中详细说明了这种方法好。

因为生成器包含离散变量，直接应用梯度估计的方法无法使用。基于 score function 的强化学习算法，例如 Monte Carlo 估计，可以得到离散变量梯度的无偏估计值。但是，这种方法的梯度估计值的方差会很大，因此，这里作者采用的是用 soft-argmax 函数来逼近 (*) 式：

$y_{t-1}=W_e\text{softmax}(Vh_{t-1}\odot L) \\$

这里的生成器的损失，当 $L\rightarrow \infty$ ，逼近越接近 (*) 式。

梯度下降的优化策略往往会因为在鞍点附近徘徊而难以收敛至纳什均衡。一个好的初始化往往能加快收敛速度。本篇论文的初始化非常有意思，对于生成器，作者预训练了一个标准自编码 LSTM 模型来初始化生成器的 LSTM 参数；对于判别器，作者使用了一种 confusion 训练策略，利用原始的句子和该句子中随机交换两个词的位置后得到的新句子进行判别训练。(在初始化的过程中，运用逐点分类损失函数对判别器进行优化)。之所以进行交换操作而不进行增加/删除操作，是因为作者希望 CNN 学习到句子结构上的特征，而不是某些单词的特征，将两个单词互换位置，输入的数据信息实际上是基本相同的，大多数卷积计算最终会得出完全相同的值。这种方法能够避免生成器通过产生重复的“realistic”单词来试图获取更高分数以欺骗判别器。

在实验中，作者交替地对生成器和判别器进行训练，每训练5次生成器就训练1次判别器，因为 LSTM 的参数比 CNN 更多，更难训练，这与原始的 GAN 训练过程相反。

论文四、《Adversarial Feature Matching for Text Generation》ICML 2017

1、写作动机

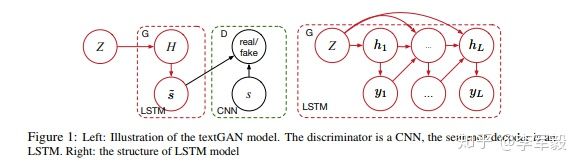
这篇论文是论文三的续作，着重叙述对抗训练的过程。训练时的目标函数不是原始 GAN 的目标函数，而是通过 kernelized discrepancy metric 对真实句子和生成句子的隐藏特征表示进行 match 操作。这种方法可以缓解对抗训练中的模式崩溃（mode collapse）问题。

什么是模式崩溃（mode collapse）？
真实世界中的数据分布可能会有多个样本集中的“波峰”。例如，假设有一个数据集，其中包含澳大利亚中部爱丽丝泉（通常非常热）和南极南极（通常非常寒冷）的夏日温度读数的混合数据。数据的分布是双峰的 - 两个地区的平均温度存在峰值，两者之间存在差距。如上图。
现在我们想训练一个产生合理温度值的 GAN。直观地说，我们希望生成器学会以几乎相等的概率产生热和冷的温度。然而，通常遇到的问题是模式崩溃，导致生成器仅从单一模式输出样本（例如，仅低温）。为什么会这样？可以考虑以下情形：
1、生成器学习到它可以通过产生接近南极温度的值来欺骗判别器认为它正在输出实际温度。
2、判别器通过了解所有澳大利亚温度都是真实的（不是由生成器产生的）而对生成器进行反驳，并且猜测南极温度是真实的还是虚假的，因为它们无法区分。
3、该生成器切换模式使得产生的值接近澳大利亚的温度来欺骗判别器，放弃南极模式。
4、判别器现在假设澳大利亚所有的温度都是假的，而南极的温度是真实的。
5、返回到第1步。
这种猫捉老鼠的游戏总是重复让人厌烦，生成器也从未被直接激励来覆盖这两种模式。在这种情况下，生成器在生成的样本中将表现出非常差的多样性，这限制了 GAN 的使用。

论文同样使用 LSTM 作为生成器，CNN 作为判别器。作者还考虑了再生核希尔伯特空间（Reproducing Kernel Hilbert Space, RKHS）下基于核的矩匹配模式（kernel-based moment-matching scheme），它能够使得真实句子和生成句子的经验分布在隐藏向量空间上有匹配的矩。这种方法能够很好地缓解原始 GAN 训练中的模式崩溃问题。

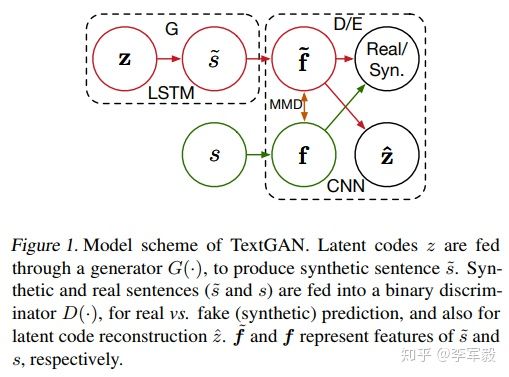
2、模型解读

原始的 GAN 模型优化目标是：

$L_{GAN}=\mathbb{E}_{x\sim p_x}\log D(x) + \mathbb{E}_{z\sim p_z}\log [1-D(G(z))] \tag{1}\\$

在论文一中我们知道，当判别器达到最优解时，这个优化目标就等于最小化 p_x 和 p_z 的JS-散度问题。但是，在大多数情况下，式（1）在鞍点附近没有很好地解决办法，所以交替更新生成器和判别器是常用的选择。

给定一个语料集，与其直接优化式（1），作者采取了一种类似 feature matching 的方法。作者的目标函数是：

$\begin{align} L_{D}&=L_{GAN}-\lambda_rL_{recon}+\lambda_mL_{MMD^2} \tag{2} \\ L_G&=L_{MMD^2} \tag{3} \\ L_{GAN}&=\mathbb{E}_{s\sim S}\log D(s)+\mathbb{E}_{z\sim p_z}\log [1-\log[1-D(G(z))]] \tag{4} \\ L_{recon}&=||\hat{z}-z||^2 \tag{5} \\ \end{align}$

L_D 和 L_G 分别是对 $D(\cdot)$ 和 $G(\cdot)$ 的最大化和最小化函数。 $L_{GAN}$ 是原始 GAN 的目标函数（1）。 $L_{recon}$ 表示初始隐藏向量和重构隐藏向量 $\hat{z}$ 之间的欧氏距离，来自先验分布 p_z 。作者定义生成的句子为 $\hat{s}$ 且 $\hat{s}\triangleq G(z)$ ， $z\sim p_z(\cdot)$ 。 $L_{MMD^2}$ 表示真实句子和生成句子的特征矩阵和 $\hat{f}$ 经验分布的 MMD 值。具体如下图所示：

MMD：maximum mean discrepancy。最大平均差异。最先提出的时候用于双样本的检测（two-sample test）问题，用于判断两个分布p和q是否相同。它的基本假设是：如果对于所有以分布生成的样本空间为输入的函数f，如果两个分布生成的足够多的样本在f上的对应的像的均值都相等，那么那么可以认为这两个分布是同一个分布。现在一般用于度量两个分布之间的相似性。

优化函数解读：

对于生成器来说，考虑式（3），它的目标是使得生成的句子 $\hat{s}$ 能够尽量模仿真实句子，这就需要计算特征矩阵 $\hat{f}$ 和的经验分布之间的 MMD 值。

对于判别器来说，考虑式（2），它的目标是希望生成的特征矩阵和 $\hat{f}$ 能够具有 discriminative，representative 以及 challenging 三种特性。这分别体现在式（2）的三部分中：i) $L_{GAN}$ 保证了真实句子和生成句子的特征矩阵和 $\hat{f}$ 具有 discriminative 特性；ii) $L_{recon}$ 保证了生成句子的特征矩阵 $\hat{f}$ 最大程度保留原始信息，即 representative 特性，也就是重构表示 $\hat{z}$ 和初始输入的欧氏距离较小；iii) $L_{MMD^2}$ 保证判别器选择最 challenging 的特征与生成器进行特征匹配 (feature matching) 。

论文五、《SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient》

AAAI 2017

1、写作动机

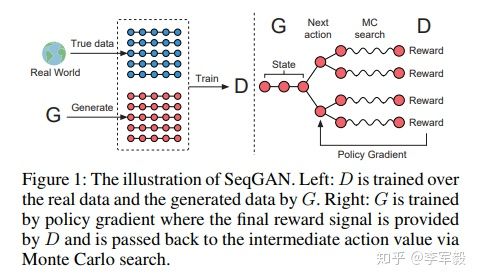
GAN 在生成连续离散序列时会遇到两个问题：一是因为生成器的输出是离散的，梯度更新从判别器传到生成器比较困难；二是判别器只有当序列被完全生成后才能进行判断，但此刻指导用处已不太大，而如果生成器生成序列的同时判别器来判断，如何平衡当前序列的分数和未来序列的分数又是一个难题。在这篇论文中，作者提出了一个序列生成模型——SeqGAN ，来解决上述这两个问题。作者将生成器看作是强化学习中的 stochastic policy，这样 SeqGAN 就可以直接通过 gradient policy update 避免生成器中的可导问题。同时，判别器对整个序列的评分作为强化学习的奖励信号可以通过 Monte Carlo 搜索传递到序列生成的中间时刻。

具体来说，作者将生成器生成序列的过程看做是一个强化学习中的序列决策过程。生成模型被看作一个 agent，目前为止已生成的序列表示当前 state，下一个要生成的单词则是采取的 action，判别模型对序列的评价分数则是返回的 reward。

2、问题定义

给定一个真实世界的序列数据集。

1）训练以 $\theta$ 为参数的生成模型 $G_{\theta}$ ，生成序列 $Y_{1:T}=(y_1,\cdots ,y_t,\cdots ,y_T),y_t \in V$ ，是词典。我们将这个问题建立在强化学习基础上。在时间步 t，状态 s 是当前已生成序列 $(y_1,\cdots ,y_{t-1})$ ，动作 a 是下一个选择的单词 y_t ，策略 policy是生成器 $G_{\theta}(y_t|Y_{1:t-1})$ ，当下一步动作选择之后，状态转换是确定的，即 $\delta^a_{s,s'}=1$ 当下一个状态 $s'=Y_{1:t}$ ，当前状态 $s=Y_{1:t-1}$ ，动作 a=y_t ；如果下一步是其他状态 s'' ，则 $\delta^a_{s,s^{''}}=0$ 。

2）训练以 $\phi$ 为参数的判别模型，指导生成器的生成。 $D_{\phi}(Y_{1:T})$ 表示序列 $Y_{1:T}$ 来自真实数据中的概率。

如上图，左边是判别器的训练，通过输入来自真实数据的正样例和来自生成器生成的负样例从而训练，判别器由 CNN 组成；右边是生成器的训练，通过将判别器判别的概率回传给生成器从而训练，这里使用了 Monte Carlo search 和 policy gradient 方法。

3、Policy Gradient

生成模型（policy） $G_\theta(y_t|Y_{1:t-1})$ 的目标是最大化期望奖励：

$J(\theta)=\mathbb{E}[R_T|s_0,\theta]=\sum_{y_1 \in V}^{}{G_\theta(y_1|s_0)\cdot Q^{G_\theta}_{D_\phi}(s_0,y_1)} \tag{1} \\$

其中 R_T 是完全生成序列的奖励，来自判别器 $D_\phi$ ， $Q^{G_\theta}_{D_\phi}(s,a)$ 是整个序列的 action-value function，表示从状态开始，依据策略 $G_\theta$ 采取动作直到结束所得到的期望累计奖励。所以，最重要就是如何计算 action-value function。

在这篇论文中，作者将判别器 $D_\phi(Y^n_{1:T})$ 判断序列 $Y^n_{1:T}$ 为真的概率作为奖励，即：

$Q^{G_\theta}_{D_\phi}(a=y_T,s=Y_{1:T-1})=D_\phi(Y_{1:T}) \tag{2} \\$

但是，前面已经说明，判别器只能当序列被完全生成之后才能返回一个奖励。因为我们在每一个时间步上，真正关心的是长期的收益，所以我们不仅应该考虑已生成序列的效果，也要考虑接下来生成的结果，这就好比在下棋时，我们会适当放弃一些眼前优势从而追求长远的胜利。因此，为了估计中间时间步上的 action-value，我们使用 Monte Carlo 搜索和 roll-out policy $G_\beta$ 来对剩下的 T-t 个未知单词进行采样。我们将这个 N 次 Monte Carlo 搜索过程表示为：

$\{Y^1_{1:T},\cdots,Y^N_{1:T}\}=\text{MC}^{G_\beta}(Y_{1:t};N) \tag{3}\\$

roll-out 算法是对于当前状态，从每一个可能的动作开始，之后根据给定的策略进行路径采样，根据多次采样的奖励总和来对当前状态的行动值进行估计。当当前估计基本收敛时，会根据行动值最大的原则选择动作进入下一个状态再重复上述过程。在蒙特卡洛控制中，采样的目的是估计一个完整的，最优价值函数，但是roll-out中的采样目的只是为了计算当前状态的行动值以便进入下一个状态，而且这些估计的行动值并不会被保留。在roll-out中采用的策略往往比较简单被称作 roll-out 策略 (roll-out policy)。

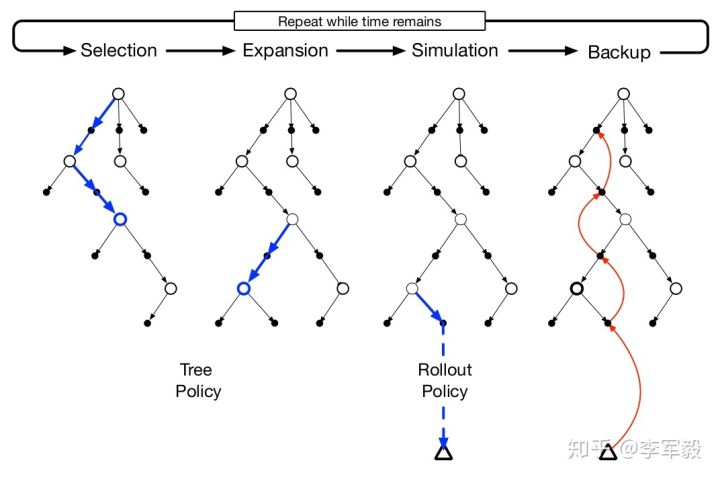
蒙特卡洛树搜索是上面提到的 roll-out 算法的拓展版，在于它会记录搜索过程中的行动值变化以便更好的采样，完整的步骤有以下四步：
1、选择：从根节点出发，根据 树策略(tree policy)选择一个叶节点
2、拓展：有一定概率发生，从选择的叶节点中执行一个未执行过的行动来增加一个子节点
3、模拟：从当前叶节点开始，根据 roll-out 策略执行动作直到终止时间
4、回溯：利用本次模拟中得到的奖励和逐层更新所使用到的树内节点
如下图所示。

进行 N 次Monte Carlo 搜索之后，我们将得到一个 batch 为 N 的输出样例。因此，

$Q^{G_\theta}_{D_\phi}(s=Y_{1:t-1},a=y_t)=\left\{ \begin{array}{rcl} \frac {1}{N}\sum \nolimits_{n=1}^{N}{D_\phi (Y^n_{1:T}),Y^n_{1:T}\in \text{MC}^{G_\beta}(Y_{1:t};N)} & \text{for} & t<T\\ D_\phi(Y_{1:t}) & \text{for} & t=T \tag{4} \end{array} \right .$

使用判别器 $D_\phi$ 作为奖励函数的好处在于奖励值可以动态地更新从而循环地改进生成模型的效果。论文中指出，每当我们生成许多与真实数据相像的序列，我们就要重新训练一次判别器：

$\min \limits_\phi -\mathbb{E}_{Y\sim p_{data}}(\log D_\phi (Y))-\mathbb{E}_{Y\sim G_\theta}[\log(1-D_\phi(Y))] \tag{5} \\$

每当重新训练得到新的判别器之后就可以更新生成器。文中采用的是 policy gradient 的方法，式（1）关于生成器中参数 $\theta$ 的梯度为：

$\nabla J(\theta)=\sum \nolimits_{t=1}^{T}{\mathbb{E}_{Y_{1:t-1}\sim G_\theta}}[\sum_{y_t \in V}^{}{\nabla_\theta G_\theta (y_t|Y_{1:t-1})\cdot Q^{G_\theta}_{D_\phi}(Y_{1:t-1},y_t)}] \tag{6}\\$

之后，更新参数 $\theta$ ：

$\theta\leftarrow \theta+\alpha_h \nabla_\theta J(\theta) \\$

具体推导过程可以参考论文附录。下图是整个算法：

论文六、《MaskGAN: Better Text Generation via Filling in the ____》ICLR 2018

1、写作动机

作者认为，以往的神经文本生成模型，例如 seq2seq，是机器翻译，摘要提取的基本模型，它们通常利用 maximun likelihood 和 teacher forcing 进行训练，生成文本的质量也都通过 validation perplexity 来定义。这些训练方法对于 perplexity 的优化来说可能很合适，但却不能保证生成文本的质量足够好，因为生成文本时，历史生成单词可能在训练时没有出现过，导致误差逐渐累积，也就是常说的 exposure bias 问题。虽然之前已经有 Professor Forcing 和 Scheduled Sampling 来解决这些问题，但它们都没有针对输出明确定义一个损失函数来提高结果质量，这篇论文对此做了改变。另外，离散输出也是导致梯度不能反向传播训练的原因，作者在这篇论文中利用强化学习中的 actor-critic 算法来训练生成器，利用最大似然和随机梯度下降来训练判别器。最后，GAN 模型中的模式崩溃和训练不稳定问题在文本生成任务下也更严重。训练不稳定会随着句子的长度增加而加重。为了避免这两个问题的影响，作者选择了基于上下文环境对缺失单词进行填充的场景。

2、模型定义

(x_t,y_t) 表示输入输出 token 对， <m> 表示 token 遮住符号， $\hat{x}_t$ 表示遮住的原始 token， $\tilde{x}_t$ 表示生成的 token。

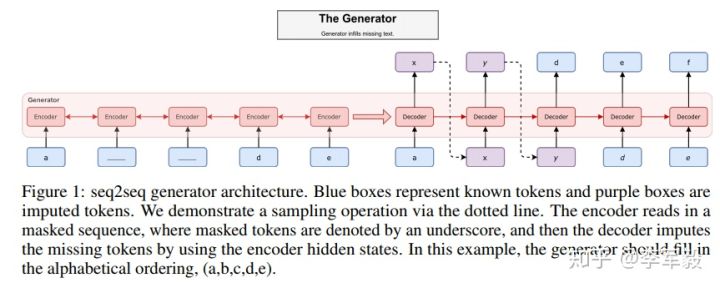
计算被遮住的 token 需要我们的 MaskGAN 模型基于历史和将来的信息。生成器由 seq2seq 模型组成。对一个输入序列 $x=(x_1,\cdots ,x_T)$ ，随机或者确定地生成一个二进制向量 $m=(m_1,\cdots ,m_T)$ ， $m_t \in \{0,1\}$ 。如果 m_t=0 ，则输入序列中的 x_t 被 <m> 替换，否则不变。seq2seq 模型中的 encoder 将这个遮住部分 token 的序列编码为一个表示，记 m(x) 。在 decoder 中的时间步 t，当我们在生成被遮住的 token 时，不仅依赖于 m(x) ，也依赖到目前为止被补充的完整序列 $(\hat{x}_1,\cdots ,\hat{x}_{t-1})$ ，所以

$P(\hat{x}_1,\cdots , \hat{x}_T|m(x))=\prod_{t=1}^{T}P(\hat{x}_t|\hat{x}_1,\cdots ,\hat{x}_{t-1},m(x)) \\$

$G(x_t) \equiv P(\hat{x}_t|\hat{x}_1,\cdots ,\hat{x}_{t-1},m(x)) \\$

判别器的模型同样也是 seq2seq 模型，它的encoder 输入是已经被生成器补充后的序列，同时还要给定被部分遮住的序列 m(x) ，decoder 在每个时间步的输出不再是一个词典上的 token 概率分布，而是一个0到1之间的概率（标量）。所以

$D_\phi (\tilde{x}_t|\tilde{x}_{0:T},m(x))=P(\tilde{x}_t=x^{real}_t|\tilde{x}_{0:T},m(x)) \\$

最后的奖励函数为：

$r_t \equiv\log D_\phi (\tilde{x}_t|\tilde{x}_{0:T},m(x)) \\$

最后一个部分则是 critic 网络，critic 网络的作用是对做出的动作估计 value function，这里表示填充后的序列总的折扣收益： $R_t=\sum_{s=t}^{T}{\gamma^sr_s}$ ， $\gamma$ 表示每一个位置上的折扣率。

3、训练目标

这篇论文同样是利用 policy gradient 方法对生成器的参数 $\theta$ 进行训练。生成器优化目标则是最大化累积总奖励 $R=\sum \nolimits_{t=1}^{T}{R_t}$ 。所以，我们通过对 $\mathbb{E}_{G(\theta)}[R]$ 进行梯度上升操作来优化生成器的参数 $\theta$ 。

论文七、《Long Text Generation via Adversarial Training with Leaked Information》

AAAI 2018

1、写作动机

作者认为，虽然之前已经有许多研究将 policy gradient 方法运用到 GAN 的文本生成任务中，也取得了一些成功，但这些方法最后返回的奖励只有当生成器完全生成序列之后才能得到，序列生成过程中缺乏一些关于序列结构的中间信息的反馈，而且，这个奖励标量没有太多关于序列语义结构方面的信息量，无法起到特别大的指导作用，这些限制了序列生成的长度（一般不大于20）。在这篇论文中，作者提出了一个 LeakGAN 模型来解决长文本生成的问题。判别器会在中间时间步泄露一些提取的特征给生成器，生成器则利用这个额外信息指导序列的生成。

2、模型定义

如上图，在生成器中，作者使用的是 hierarchical reinforcement learning 结构，包括 Manager 模块和 Worker 模块。Manager 模块是一个 LSTM 网络，充当中介的一个角色。在每个时间步上，它都会从判别器中接收一个特征表示（例如，CNN 中的 feature map），然后将它作为一个指导信号传递为 Worker 模块。因为判别器的中间信息在原始的 GAN 中是不应该被生成器知道的，所以作者把这个特征表示称为泄露的信息。接收到这个指导信号的 embedding 之后，Worker 模块同样也利用 LSTM 网络编码当前输入 x_t ，然后将 LSTM 的输出和收到的指导信号 embedding 连接在一起共同计算下一步的动作，即选择下一个单词。

泄露的特征表示：

传统的 RL 下，模型的 reward functi\ $\phi=(\phi_f,\phi_l)$ on 一般是个黑匣子，而在这个对抗文本生成模型中，作者使用判别器 $D_\phi$ 作为可学习的 reward function， $D_\phi$ 可以分解为一个特征提取器 $F(\cdot;\phi_f)$ 和一个权重为 $\phi_l$ 的 sigmoid 分类层。数学化表示为，给定一个输入，有

$D_\phi(s)=\text{sigmoid}(\phi_l^{\text{T}}F(s;\phi_f))=\text{sigmoid}(\phi_l^{\text{T}}f) \tag{1}\\$

这里的 $\phi=(\phi_f,\phi_l)$ ， $f=F(s;\phi_f)$ 是输入的特征向量，也就是泄露给生成器的中间信息。从式（1）可以看出，判别器对每一时刻的状态的奖励值依赖于提取出的特征。也正因为这样，从判别器 $D_\phi$ 中获得一个高奖励值的优化目标可以等价为在特征空间 $F(S;\phi_f)=\{F(s;\phi)\}_{s\in S}$ 中找到一个高奖励值的的区域。相比于之前奖励值为标量的模型，特征向量可以提供更多的指导信息给生成器。

生成器层次结构：

Manager：LSTM 的初始化状态为 h^M_0 ，在每个时间步上，以泄露的特征向量 f_t 为输入，输出目标向量 g_t ，如下式：

$\hat{g}_t,h^M_t=M(f_t,h^M_{t-1};\theta_m) \\$

$g_t=\hat{g}_t/||\hat{g}_t|| \\$

为了结合 Manager 产生的目标向量 g_t ，作者对最新的 c 个目标向量进行求和并进行权重为 $W_\psi$ 的线性变换，得到一个 k 维的目标嵌入 w_t ：

$w_t=\psi(\sum_{i=1}^{c}{g_{t-i}})=W_\psi(\sum_{i=1}^{c}{g_{t-i}}) \\$

Worker：以当前单词 x_t 为输入，输出一个矩阵 O_t ，它将通过矩阵乘法和目标嵌入 w_t 连接在一起，决定下一步动作的概率分布：

$O_t,h^W_t=W(x_t,h^W_{t-1};\theta_w) \\$

$G_\theta(\cdot|s_t)=\text{softmax}(O_t\cdot w_t/\alpha) \\$

3、训练生成器

在 LeakGAN 模型中，作者对生成器中的 Manager 模块和 Worker 模块分别训练。Manager 模块的训练目标是要在判别器的特征空间中找到有利的指导方向，Worker 模块的训练目标是遵循这个方向以得到奖励。

Manager 模块的梯度为：

$\nabla^{adv}_{\theta_m}g_t=-Q_{F}(s_t,g_t)\nabla_{\theta_m}d_{cos}(f_{t+c}-f_t,g_t(\theta_m)) \\$

其中 $Q_F(s_t,g_t)=Q(F(s_t),g_t)=Q(f_t,g_t)=\mathbb{E}[r_t]$ ，是当前策略下的预期奖励，可以通过 Monte Carlo 搜索近似估计。 $d_{cos}$ 表示 c 步之后特征向量的改变 $f_{t+c}-f_t$ 和目标向量 $g_t(\theta_m)$ 之间的余弦相似度。损失函数要求目标向量匹配特征空间的转换，同时获得更高奖励。同时，Worker 模块要最大化这个奖励，这可以通过对状态 $s_{t-1}$ 和动作 x_t 进行采样来近似。

$\nabla_{\theta_m}\mathbb{E}_{s_{t-1}\sim G}[\sum_{x_t}^{}{r^I_tW(x_t|s_{t-1};\theta_w)}]=\mathbb{E}_{s_{t-1}\sim G,x_t\sim W(x_t|s_{t-1})}[r^I_t\nabla_{\theta_m}\log W(x_t|s_{t-1};\theta_w)] \\$

当鼓励 Worker 模块遵循 Manager 指示的方向时，Worker 的内在奖励定义为：

$r^I_t=\frac {1}{c}\sum_{i=1}^{c}{d_{cos}(f_t-f_{t-i},g_{t-i})} \\$

GAN+文本生成：让文本以假乱真

扫码关注一起随时随地学习！！！就在洋葱攻城狮，更多精彩，等你来！！

悦读