扩散模型（公式推导）

本文很大程度上参考了Diffusion Model 扩散模型-[通俗易懂+代码讲解]（一） - 知乎 (zhihu.com)以及https://blog.csdn.net/m0_63642362/article/details/127586200，https://segmentfault.com/a/1190000043744225
三篇文章都写得非常好
本文相当于作者自己的一个学习笔记。在一些步骤上进行了补充，但由于博主刚开始学习，还是存在一些不理解的地方。

模型训练

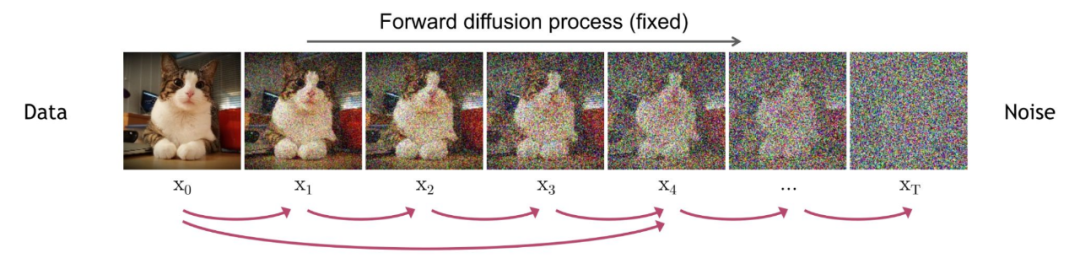
1. 前向扩散过程（Forward Diffusion Process）→图片中添加噪声；

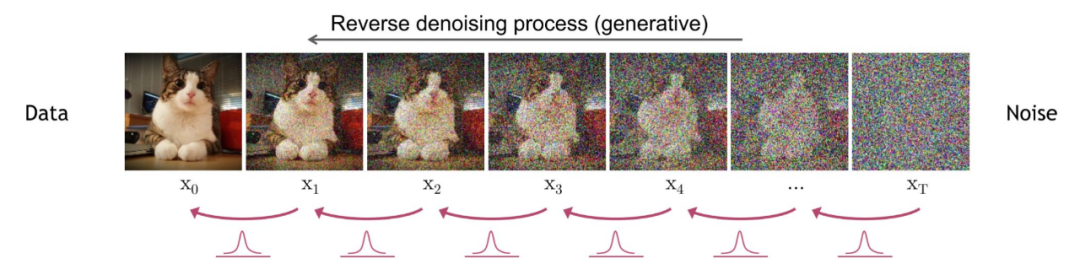
2. 反向扩散过程（Reverse Diffusion Process）→去除图片中的噪声

前向扩散过程：不断往其中添加高斯噪声

反向扩散过程：将噪声逐渐还原为原始图片

一些前置知识：

给定两个服从正态分布的独立随机变量 $X\sim N({\mu }_X,{\sigma }_X^2),Y\sim N({\mu }_Y,{\sigma }_Y^2)$，这两个分布的加和 $Z=X+Y$，同样服从正态分布 $Z\sim N({\mu }_X+{\mu }_Y,{\sigma }_X^2+{\sigma }_Y^2)$。这意味着两个独立正态分布随机变量的和是正态的，其平均值是两个平均值的和，其方差是两个方差的和。

前向扩散过程推导

定义前向传播过程：给定一组从真实数据分布中采样的数据 $x_0\sim q(x)$，即原始数据，分 T（注意，此处的 T 在训练过程中是一个可变参数）步来一步步对该样本叠加高斯噪声，最终的得到一系列经噪声叠加后的样本 $x_1,x_2,\dots ,x_T$，其中，步数 T 的大小受 ${\beta }_t$ 约束(${\beta }_t\in (0,1){\}}_{t=1}^T$)。

(目的：使得数据分布逐渐趋于一个一致的简单分布（通常是标准正态分布）。这个过程可以表示为一个马尔科夫链，其中每一步的状态$x_t$ 都依赖于前一步的状态 $x_{t-1}$。)

$q(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$ q表示已知$x_{t-1}$时$x_t$的概率分布，它是一个多元高斯分布。

参数分别为（当前状态，均值，协方差矩阵）。

我们想要表达从初始状态 $x_0$ 开始，到时刻 $T$ 的所有状态 $x_1,x_2,\dots ,x_T$ 的联合分布 $q(x_{1:T}\mid x_0)$。

已知全概率公式形式为：

$P(A)={\sum }_{i}P(A\mid B_i)P(B_i)$

同时我们有

$P(A,B)=P(A\mid B)P(B)$（AB联合分布概率，可以理解为同时发生的概率）

对于多个事件 $X_1,X_2,\dots ,X_n$，联合概率分布可以写成条件概率的乘积：

$P(X_1,X_2,\dots ,X_n)=P(X_1)P(X_2\mid X_1)P(X_3\mid X_1,X_2)\cdots P(X_n\mid X_1,X_2,\dots ,X_{n-1})$

根据链式法则，对于随机变量序列 $X_0,X_1,\dots ,X_T$，我们有：

$q(x_0,x_1,\dots ,x_T)=q(x_0)q(x_1\mid x_0)q(x_2\mid x_0,x_1)\cdots q(x_T\mid x_0,x_1,\dots ,x_{T-1})$

在扩散模型中，我们假设每个状态 $x_t$ 只依赖于前一个状态 $x_{t-1}$ （马尔科夫性质），即：

$q(x_t\mid x_0,x_1,\dots ,x_{t-1})=q(x_t\mid x_{t-1})$

因此，联合概率分布可以简化为：

$q(x_0,x_1,\dots ,x_T)=q(x_0)q(x_1\mid x_0)q(x_2\mid x_1)\cdots q(x_T\mid x_{t-1})$

在给定初始状态 $x_0$ 的情况下，所有中间状态的条件联合分布为：

$q(x_{1:T}\mid x_0)=q(x_1\mid x_0)q(x_2\mid x_1)\cdots q(x_T\mid x_{t-1})={\prod }_{t=1}^{T}q(x_t\mid x_{t-1})$

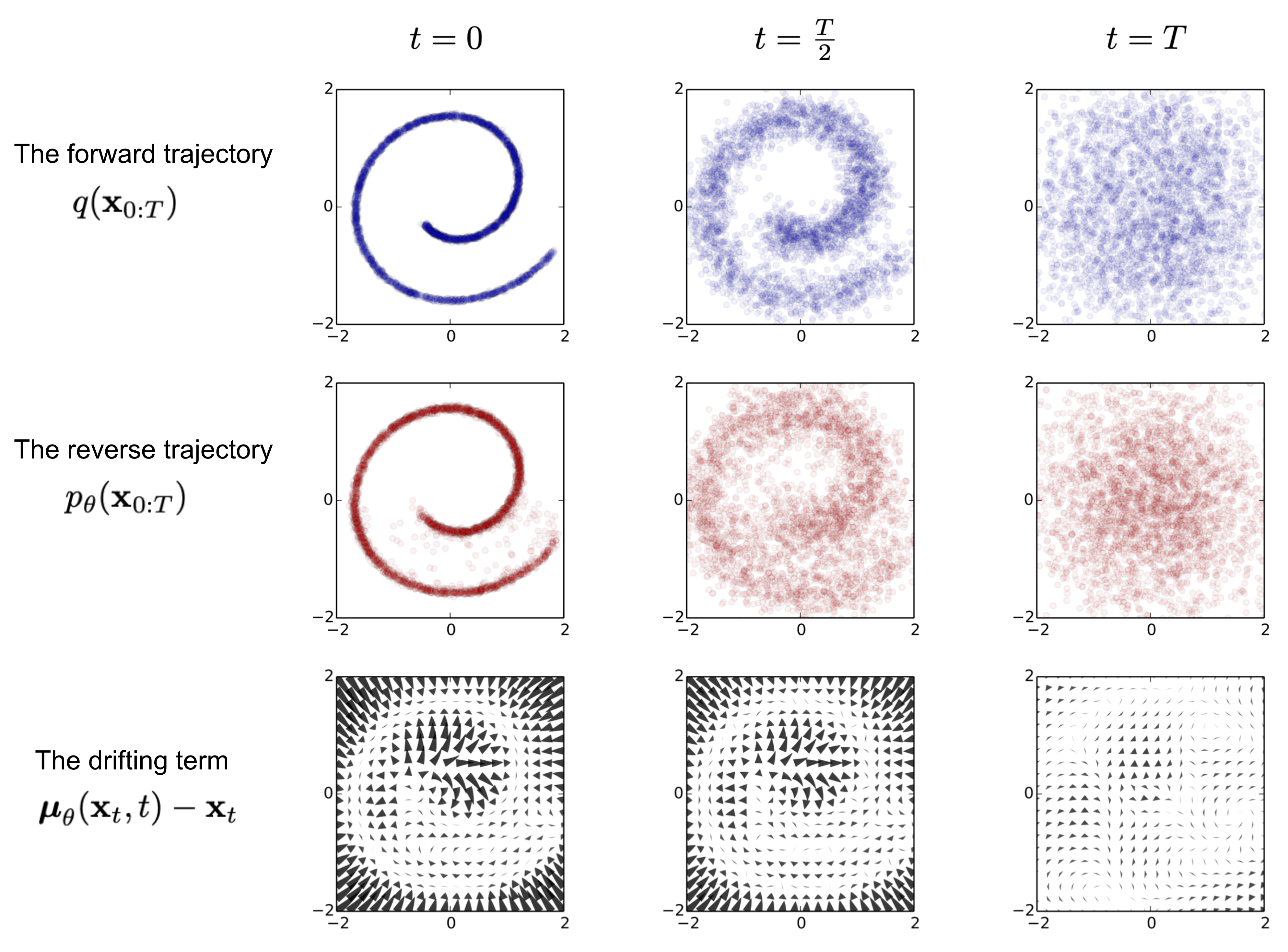
其间，原始数据 $x_0$ 在前向扩散的 $t$步数的迭代，逐渐失去其独特鲜明的特征，最终当 $T\to \infty$，$x_T$ 等价于一个符合各向同性的高斯分布噪声，如图所示。

往右边就是前向扩散，往左边就是逆向扩散

高斯噪声（Gaussian noise）,也叫做白噪声 :概率密度函数遵循高斯分布（也称为正态分布）

在任意时间步 $t$ 的 $x_t$ 进行采样。这里定义 ${\alpha }_t=1-{\beta }_t$ 且 ${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$，给定高斯噪声：${ϵ}_{t-1},{ϵ}_{t-2},\cdots \sim N(0,I)$。

$x_t=\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}$ （这里开始，相当于每一步加一点噪声）

$=\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-2}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}$

$\sqrt{1-{\alpha }_t}{ϵ}_{t-1}$ 和 $\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-2}$ 分别表示 ${ϵ}_{t-1}\sim N(0,{\sigma }_1^{2}I)$ 和 ${ϵ}_{t-2}\sim N(0,{\sigma }_2^{2}I)$ ，方差变为原分布的 $(1-{\alpha }_t)$ 与 $({\alpha }_t-{\alpha }_t{\alpha }_{t-1})$ 倍，

新的分布加和得到 ${ϵ}_{t-2}\sim N(0,({\sigma }_1^2+{\sigma }_2^2)I)$，该分布方差为 $({\alpha }_t-{\alpha }_t{\alpha }_{t-1})+1-{\alpha }_t=1-{\alpha }_t{\alpha }_{t-1}$ 的倍数。

$x_t=\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{ϵ}}_{t-2}$
$=\cdots =\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$ 其中，${\overline{ϵ}}_{t-2}$ 为合并两个高斯分布 ${ϵ}_{t-1}$ 和 ${ϵ}_{t-2}$ 后的分布表示。

由此推导出的公式记为 $x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$ （由原始公式推导出来）

这样就可以得到在已知$x_0$的情况下，$x_t$的概率分布为：
$q(x_t\mid x_0)=N(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$
(这个是由于噪声的均值为0，协方差为$I$)

逆向扩散过程（Reverse diffusion process）

扩散过程是将数据噪音化，反向过程就是一个去噪的过程。逆向扩散过程中，我们将以高斯噪声 $x_T\sim N(0,I)$ 作为输入，从 $q(x_{t-1}\mid x_t)$ 中采样，推断并重构出真实样本。

训练出一个模型来对这些噪声的条件概率进行预测:
将前向传播每步生成的真实噪声记录下来作为标签，在模型做逆向扩散时，即可对前向扩散中所产生的高斯噪声进行预测，并一步一步推断，以还原最初始的样本数据。

而在去除 $x_{t-1}$ 所加的高斯噪声的后验估计分布为：

$p_{\theta }(x_{t-1}\mid x_t)=N(x_{t-1};{\mu }_{\theta }(x_t,t),{\sum }_{\theta }(x_t,t))$ 这里面的参数代表神经网络估计的值

虽然分布 $q(x_{t-1}\mid x_t)$ 是无法直接计算得到的，但是加上条件 $x_0$ 的后验分布 $q(x_{t-1}\mid x_t,x_0)$ 即可通过计算处理而得。

$q(x_{t-1}\mid x_t,x_0)=q(x_{t-1}\mid x_t)=N(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_{t}I)$
（最左边的式子表示在已知$x_t$和已知$x_0$的情况下$x_{t-1}的概率$，别搞错了）

公式推导

• 联合概率可以通过条件概率表示为：
  $q(x_{t-1},x_t\mid x_0)=q(x_t\mid x_{t-1},x_0)q(x_{t-1}\mid x_0)$

• 同时，也可以表示为：
  $q(x_{t-1},x_t\mid x_0)=q(x_{t-1}\mid x_t,x_0)q(x_t\mid x_0)$

联立两个式子，可以得到
$q(x_{t-1}\mid x_t,x_0)=\frac{q(x_t\mid x_{t-1},x_0)q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}$

这时候右边三个式子都是已知的了

$q(x_t\mid x_0)=N(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$ *已知1

$q(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$ *已知2

那么
$q(x_{t-1}\mid x_t,x_0)=\frac{q(x_t\mid x_{t-1},x_0)q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}$

$\propto e^{-\frac{1}{2}\left(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\right)}$

$=e^{-\frac{1}{2}\left(\frac{x_t^2-2\sqrt{{\alpha }_t}{x}_t{x}_{t-1}+{\alpha }_t{x}_{t-1}^2}{{\beta }_t}+\frac{x_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{x}_{t-1}{x}_0+{\bar{\alpha }}_{t-1}{x}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\right)}$

$=e^{-\frac{1}{2}\left(\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)x_{t-1}^2-\left(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0\right)x_{t-1}+C(x_t,x_0)\right)}$

这是一个类似高斯分布的式子，观察高斯分布形式：
$e^{-\frac{1}{2}\left(\frac{(x_{t-1}-\mu {)}^2}{{\sigma }^2}\right)}$。

配方之后可以得到：

$\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)\left(x_{t-1}^2-2\left(\frac{\sqrt{{\alpha }_t}{x}_t}{{\beta }_t}+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{x}_0}{1-{\bar{\alpha }}_{t-1}}\right)x_{t-1}+{\left(\frac{\sqrt{{\alpha }_t}{x}_t}{{\beta }_t}+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{x}_0}{1-{\bar{\alpha }}_{t-1}}\right)}^2\right)$

那么均值和方差就可以表示为：

方差：

${\tilde{\beta }}_t=\frac{1}{\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)}=\frac{1}{\left(\frac{{\alpha }_t(1-{\bar{\alpha }}_{t-1})+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}\right)}=\frac{1}{\left(\frac{1-{\beta }_t-{\bar{\alpha }}_{t-1}+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}\right)}=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t$

方差的所有参数都是已知的，${\alpha }_t$,${\beta }_t$都是已知的，随t不断变化的可以设置的参数。

均值：
${\tilde{\mu }}_t(x_t,x_0)=\frac{\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0\right)}{\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)}=\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0\right)\frac{1}{\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)}=\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0\right)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t$

$=\left(\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{{\beta }_t(1-{\bar{\alpha }}_t)}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{(1-{\bar{\alpha }}_{t-1})(1-{\bar{\alpha }}_t)}{x}_0\right)=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})x_t+\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0}{{\beta }_t(1-{\bar{\alpha }}_t)}$

$=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})x_t+\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0}{1-{\bar{\alpha }}_t}$

$=\sqrt{{\alpha }_t(1-{\bar{\alpha }}_{t-1})x_t+\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0}1-{\bar{\alpha }}_t$

由于 $x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$，$x_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}ϵ)$
那么：
${\tilde{\mu }}_t=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}ϵ)$

$=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}ϵ)$

$=\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}ϵ\right)$

这个$x_t$会受到不同$x_0$影响，每次不是确定的。

优化目标

$p_{\theta }(x_{t-1}\mid x_t)=N(x_{t-1};{\mu }_{\theta }(x_t,t),{\sum }_{\theta }(x_t,t))$ 这里面的参数代表神经网络估计的值

现在，我们要预测的就是这里的${\mu }_{\theta }(x_t,t)$

我们先看整体损失函数：

$-\log (P_{\theta }(X_0))$，希望神经网络的参数 $\theta$ 可以使得生成 $X_0$ 的概率越来越大越好。

前置知识 Kullback-Leibler散度(相对熵)：用于衡量两个概率分布之间的差异。具体来说，它衡量的是当一个分布𝑞被另一个分布p 近似时，所损失的信息。

也就是说，当使用分布 $p_{\theta }$来近似分布𝑞时，会丢失多少信息。数学表达式为：
$D_{KL}(q\parallel p)={\sum }_{x}q(x)\log \frac{q(x)}{p(x)}$

由于损失函数无法直接计算，我们选择：
$-\log p_{\theta }(x_0)\le -\log p_{\theta }(x_0)+D_{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta }(x_{1:T}\mid x_0))$

$=D_{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta }(x_{1:T}\mid x_0))={\mathbb{E}}_{x_{1:T}\sim q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{1:T}\mid x_0)}\right]$

由于 $\frac{p_{\theta }(x_{0:T})}{p_{\theta }(x_0)}\leftarrow \frac{p_{\theta }(x_0,x_{1:T})}{p_{\theta }(x_0)}\leftarrow \frac{p_{\theta }(x_0\mid x_{1:T})p_{\theta }(x_{1:T})}{p_{\theta }(x_0)}$

则$=-\log p_{\theta }(x_0)+{\mathbb{E}}_{x_{1:T}\sim q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})/p_{\theta }(x_0)}\right]$

$=-\log p_{\theta }(x_0)+{\mathbb{E}}_q\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}\right]+\log p_{\theta }(x_0)$

$={\mathbb{E}}_q\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}\right]$
(由于最右边是一个常数值，对它取期望的操作相当于它本身)

（接下来的推导又会用到：
$q(x_{t-1},x_t\mid x_0)=q(x_t\mid x_{t-1},x_0)q(x_{t-1}\mid x_0)$
$q(x_{t-1},x_t\mid x_0)=q(x_{t-1}\mid x_t,x_0)q(x_t\mid x_0)$）

$E_q\left[\log \left(\frac{{\prod }_{t=1}^{T}q(x_t|x_{t-1})}{p_{\theta }(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}|x_t)}\right)\right]$

$=E_q\left[-\log p_{\theta }(x_T)+{\sum }_{t=2}^T\log \frac{q(x_t|x_{t-1})}{p_{\theta }(x_{t-1}|x_t)}+\log \frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}\right]$

$=E_q\left[-\log p_{\theta }(x_T)+{\sum }_{t=2}^T\log \frac{q(x_t|x_{t-1})}{p_{\theta }(x_{t-1}|x_t)}+\log \frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}\right]$

$=E_q\left[-\log p_{\theta }(x_T)+{\sum }_{t=2}^T\log \left(\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_{t-1}|x_0)p_{\theta }(x_{t-1}|x_t)}\right)+\log \frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}\right]$

$ =E_q \left[ -\log p_\theta (x_T) + \sum_{t=2}^{T} \log \frac{q(x_t | x_{t-1})}{p_\theta (x_{t-1} | x_t)} + \sum_{t=2}^{T} \log \frac{q(x_{t-1} | x_0)}{q(x_{t-1} | x_0)} + \log \frac{q(x_1 | x_0)}{p_\theta (x_0 | x_1)} \right]$

$=E_q\left[-\log p_{\theta }(x_T)+{\sum }_{t=2}^T\log \frac{q(x_t|x_{t-1})}{p_{\theta }(x_{t-1}|x_t)}+\log \frac{q(x_T|x_0)}{q(x_1|x_0)}+\log \frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}\right]$

$=E_q\left[\log \frac{q(x_T|x_0)}{p_{\theta }(x_T)}+{\sum }_{t=2}^T\log \frac{q(x_{t-1}|x_0)}{p_{\theta }(x_{t-1}|x_t)}-\log p_{\theta }(x_0|x_1)\right]$

$=E_q\left[D_{KL}(q(x_T|x_0)\parallel p_{\theta }(x_T))+{\sum }_{t=2}^T{D}_{KL}(q(x_{t-1}|x_t,x_0)\parallel p_{\theta }(x_{t-1}|x_t))-\log p_{\theta }(x_0|x_1)\right]$

这时候第一项没有可以学习的参数，就是一个正向过程，同时$x_T$已知

最后一项不要了

根据上文，我们现在有：
$q(x_{t-1}\mid x_t,x_0)=q(x_{t-1}\mid x_t)=N(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_{t}I)$

$p_{\theta }(x_{t-1}\mid x_t)=N(x_{t-1};{\mu }_{\theta }(x_t,t),{\sum }_{\theta }(x_t,t))$

真实值
${\tilde{\mu }}_t=\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}ϵ\right)$

参数化表示预测值
${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)\right)$

用了一种均方误差表示法来计算误差：

$L_t=\frac{1}{2{\sigma }_t^2}\Vert {\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t){\Vert }^2$

$\downarrow \text{将}\mu 的表达式代入$

$=\frac{1}{2{\sigma }_t^2}\Vert \frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}ϵ)-\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)){\Vert }^2$

$=\frac{{\beta }_t^2}{2{\sigma }_t^2{\alpha }_t(1-{\bar{\alpha }}_t)}\Vert ϵ-{ϵ}_{\theta }(x_t,t){\Vert }^2$

如果把前面的系数全部丢掉的话，模型的效果更好。最终，我们就能得到一个非常简单的优化目标：

$=\Vert ϵ-{ϵ}_{\theta }(x_t,t){\Vert }^2$