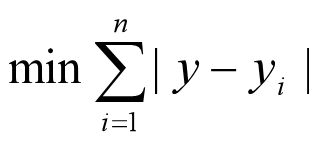目录
描述
¢
某石油公司计划建造一条
由东向西
的主输油管道。该管道要穿过一个有n口油井的油田。从每口油井都要有一条输油管道沿最短路经(或南或北)与主管道相连。
¢
如果给定
n
口油井的位置,即它们的
x
坐标(东西向)和
y
坐标(南北向),应如何确定主管道的最优位置,即使
各油井到主管道之间
的输油管道长度总和最小的位置?
¢
给定
n口油井的位置,编程计算各油井到主管道之间的输油管道最小长度总和
。
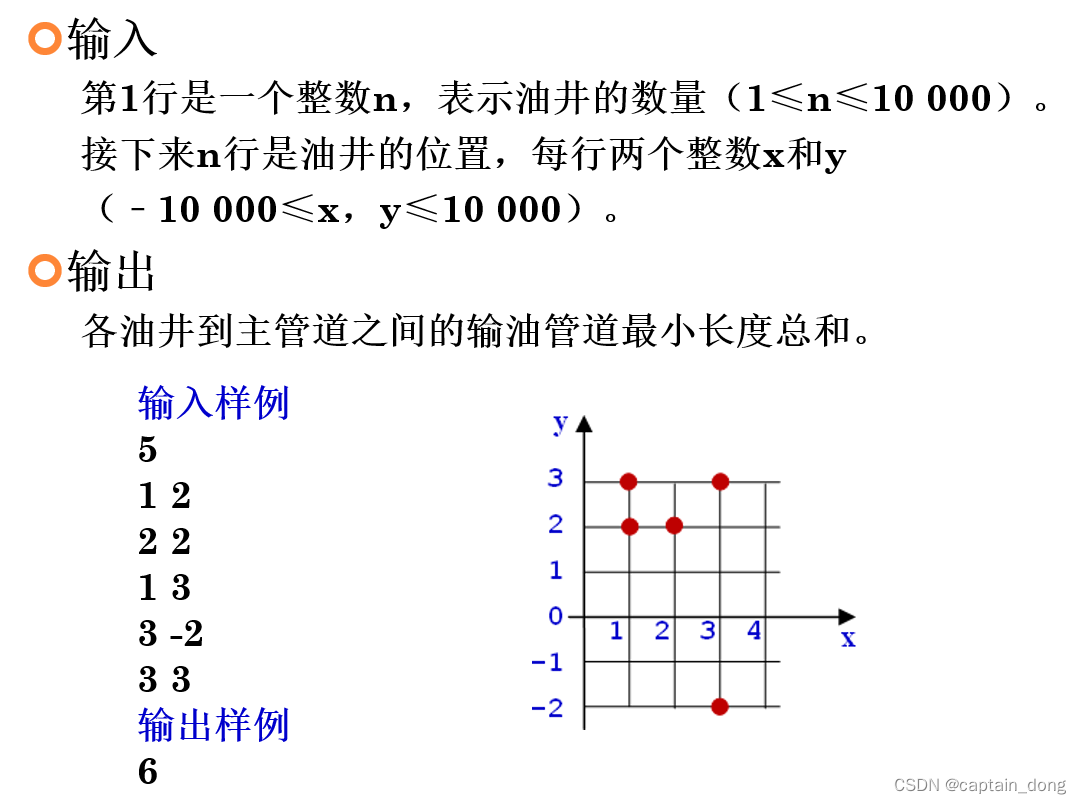
输入
第1行是一个整数n,表示油井的数量(1≤n≤10 000)。
接下来n行是油井的位置,每行两个整数x和y
(﹣10 000≤x,y≤10 000)。
输出
各油井到主管道之间的输油管道最小长度总和。
输入样例
5
1 2
2 2
1 3
3 -2
3 3
输出样例
6
分析
设n口油井的位置分别为 Pi=(xi,yi),i=1~n。由于主输油管道是东西向的,因此可用其主轴线的y坐标唯一确定其位置。主管道的最优位置y应该满足:
由中位数定理可知,y是中位数。
代码
算法1:对数组a排序(一般是升序),取中间的元素
int n; //油井的数量
int x; //x坐标,读取后丢弃
int a[1000]; //y坐标
cin>>n;
for(int k=0;k<n;k++)
cin>>x>>a[k];
sort(a,a+n); //按升序排序
//计算各油井到主管道之间的输油管道最小长度总和
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-a[n/2]);
cout<<min<<endl;
/*
* 输油管问题
*/
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
int n;//油井数量
int x;//横坐标
int a[1000];//纵坐标
cin >> n;
for (int i = 0; i < n; i++) {
cin >> x >> a[i];//输入每个油井的坐标
}
sort(a, a + n);//n个油井的y轴按大小升序排列(a-》0,a+n-》a[n])
//计算各油井到主管道之间的输油管道最小长度总和
int min=0;//初始化最小长度
for (int k = 0; k < n; k++) {
min += (int)fabs(a[k] - a[k / 2]);
}
cout << "各油井到主管道之间的输油管道最小长度总和为:";
cout << min << endl;
return 0;
}运行结果
方法二:采用分治策略求中位数
算法2:采用分治策略求中位数
int n; //油井的数量
int x; //x坐标,读取后丢弃
int a[1000]; //y坐标
cin>>n;
for (int i=0; i<n; i++)
cin>>x>>a[i];
int y = select(0, n-1, n/2); //采用分治算法计算中位数
//计算各油井到主管道之间的输油管道最小长度总和
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-y);
cout<<min<<endl;
/*
* 输油管问题--分治算法计算中位数
*/
#include<iostream>
#include<algorithm>
using namespace std;
const int NUM=1001;
int a[NUM];
//在a[left:right]中选择第k小的元素
int select(int left,int right,int k) {
if (left >= right)
return a[left];
int low = left;//从左到右的指针
int hight = right+1;//从右到左的指针
//把最左边的元素作为分界数据
int pivot = a[left];
//把左侧>=pivot的和右侧<=pivot的元素交换
while (true) {
//在左侧找出>=pivot的元素
do {
low= low+1;
} while (a[low]<pivot);
//在右侧找出<=pivot的元素
do {
hight= hight-1;
} while (a[hight]>pivot);
if (low > hight)
break;
swap(a[low], a[hight]);
}
if ((hight - left + 1 )== k)
return pivot;
a[left] = a[hight];
a[hight] = pivot;//存储pivot
if ((hight - left + 1 )< k)
//对一个段进行递归调用
return select(hight + 1, right, k-hight+left-1);
else
return select(left, hight - 1, k);
}
int main() {
int n;//油井数量
int x;//横坐标
int a[1000];//纵坐标
cin >> n;
for (int i = 0; i < n; i++) {
cin >> x >> a[i];//输入每个油井的坐标
}
int y = select(0, n - 1, n / 2);//采用分治法计算中位数
//计算各油井到主管道之间的输油管道最小长度总和
int min = 0;
for (int i = 0; i < n; i++) {
min += (int)fabs(a[i] - y);
}
cout << min<<endl;
return 0;
}