前言
系列专栏:机器学习:高级应用与实践【项目实战100+】【2024】✨︎
在本专栏中不仅包含一些适合初学者的最新机器学习项目,每个项目都处理一组不同的问题,包括监督和无监督学习、分类、回归和聚类,而且涉及创建深度学习模型、处理非结构化数据以及指导复杂的模型,如卷积神经网络、门控递归单元、大型语言模型和强化学习模型
本文旨在实现一个强大的机器学习模型,该模型可以预测乳腺癌患者是良性肿瘤还是恶性肿瘤。该模型使用k近邻算法 (KNN),k近邻算法,也称为 KNN 或 k-NN,是一种非参数、有监督的学习分类器,KNN 使用邻近度对单个数据点的分组进行分类或预测。
目录
1. 相关库和数据集
1.1 相关库介绍
XGBClassifier、支持向量分类器和决策树分类器用于根据给定数据集中的属性预测给定患者是患有恶性肿瘤还是良性肿瘤。
Pandas– 该库有助于以 2D 数组格式加载数据框,并具有多种功能,可一次性执行分析任务。Numpy– Numpy 数组速度非常快,可以在很短的时间内执行大型计算。Matplotlib/Seaborn– 此库用于绘制可视化效果。Sklearn– 包含多个库,这些库具有预实现的功能,用于执行从数据预处理到模型开发和评估的任务。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix, ConfusionMatrixDisplay
1.2 数据集介绍
我们将在此处使用的UCI机器学习存储库中的数据集,它是患有恶性和良性肿瘤的乳腺癌患者的数据集。这些列中的值是其他一些诊断的一部分,这些诊断通常用于捕获健康人与受影响的人之间的差异。现在,让我们将数据集加载到Pandas的数据框中。
data = pd.read_table('wdbc.data', sep=',', header=None, names=[
'id', 'diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean',
'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
'fractal_dimension_se', 'radius_worst', 'texture_worst',
'perimeter_worst', 'area_worst', 'smoothness_worst',
'compactness_worst', 'concavity_worst', 'concave points_worst',
'symmetry_worst', 'fractal_dimension_worst', 'Unnamed: 32'])
data.sample(5)
由于数据集的维度比较高。让我们检查数据集的哪一列包含哪种类型的数据。
df.info()
输出
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 33 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 569 non-null int64
1 diagnosis 569 non-null object
2 radius_mean 569 non-null float64
3 texture_mean 569 non-null float64
4 perimeter_mean 569 non-null float64
5 area_mean 569 non-null float64
6 smoothness_mean 569 non-null float64
7 compactness_mean 569 non-null float64
8 concavity_mean 569 non-null float64
9 concave points_mean 569 non-null float64
10 symmetry_mean 569 non-null float64
11 fractal_dimension_mean 569 non-null float64
12 radius_se 569 non-null float64
13 texture_se 569 non-null float64
14 perimeter_se 569 non-null float64
15 area_se 569 non-null float64
16 smoothness_se 569 non-null float64
17 compactness_se 569 non-null float64
18 concavity_se 569 non-null float64
19 concave points_se 569 non-null float64
20 symmetry_se 569 non-null float64
21 fractal_dimension_se 569 non-null float64
22 radius_worst 569 non-null float64
23 texture_worst 569 non-null float64
24 perimeter_worst 569 non-null float64
25 area_worst 569 non-null float64
26 smoothness_worst 569 non-null float64
27 compactness_worst 569 non-null float64
28 concavity_worst 569 non-null float64
29 concave points_worst 569 non-null float64
30 symmetry_worst 569 non-null float64
31 fractal_dimension_worst 569 non-null float64
32 Unnamed: 32 0 non-null float64
dtypes: float64(31), int64(1), object(1)
memory usage: 146.8+ KB.4 MB
根据上述有关每列数据的信息,我们可以观察到没有空值。
data.diagnosis.unique()
输出
array(['M', 'B'], dtype=object)
1.3 数据清理
从主要来源获得的数据被称为原始数据,需要大量的预处理,然后才能从中得出任何结论或对其进行一些建模。这些预处理步骤称为数据清理,它包括异常值删除、空值插补以及删除数据输入中的任何类型的差异。我们将删除列 ‘id’ 和 ‘Unnamed: 32’,因为它们在预测中没有作用
df = data.drop(['Unnamed: 32', 'id'], axis = 1)
data.diagnosis = [1 if each == "M" else 0 for each in data.diagnosis]
features = data.drop(['Unnamed: 32', 'id', 'diagnosis'], axis = 1)
target = data['diagnosis']
features.shape
2. 数据探索分析(可视化)
2.1 特征分析(可视化)
sns.set_theme(style="white")
# Initialize the figure with a logarithmic x axis
fig, axes = plt.subplots(nrows=30, ncols=1, figsize=(20, 45))
axes = axes.flatten()
for i, feature in enumerate(features):
# Plot the orbital period with horizontal boxes
sns.boxplot(x=df[feature], ax=axes[i], width=.6, color= 'plum', linecolor= 'orchid', orient='h')
# Add in points to show each observation
sns.stripplot(x= df[feature], ax=axes[i], size=3, color="orchid")
# Tweak the visual presentation
#sns.despine(ax=axes[i],trim=True, left=True)
axes[i].set_title(f'{feature}')
axes[i].set_xlabel('')
plt.tight_layout()
plt.show()
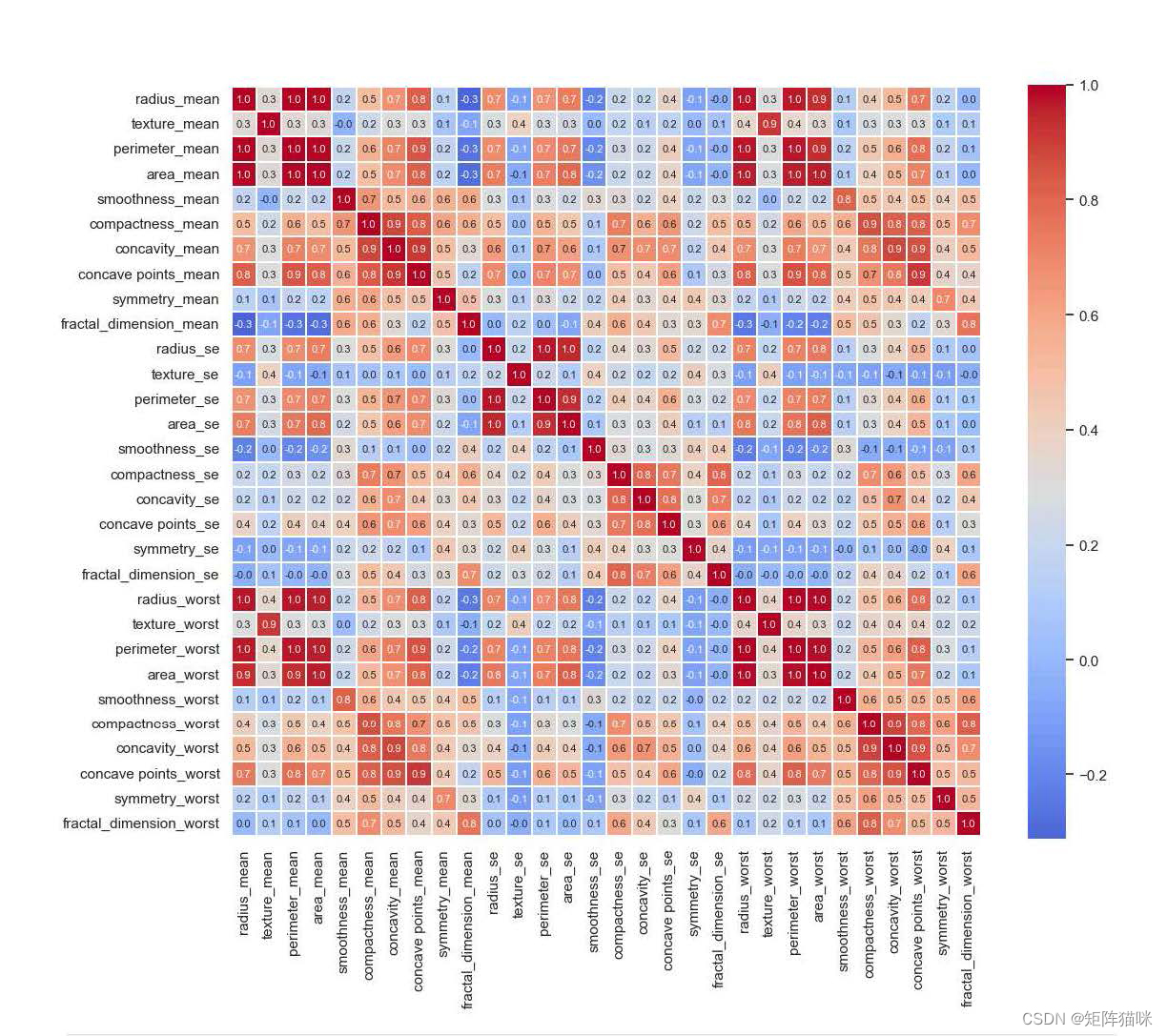
2.2 特征相关性(可视化)
plt.figure(figsize=[12, 10])
sns.heatmap(features.corr(), annot=True , fmt = '.1f', annot_kws={"fontsize": 8}, linewidths=0.25, center=0.3, cmap='coolwarm', square=True)
plt.tight_layout()
plt.show()
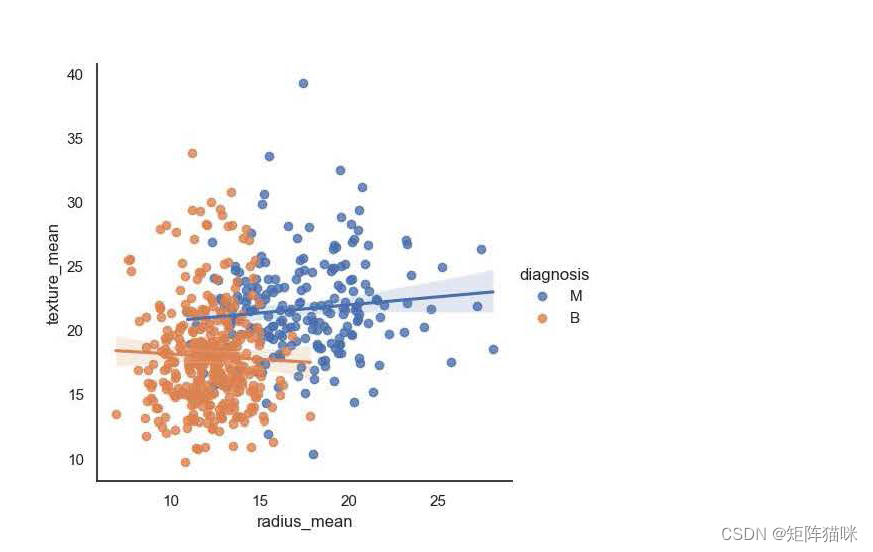
sns.lmplot(x = 'radius_mean', y = 'texture_mean', hue = 'diagnosis', data = df)
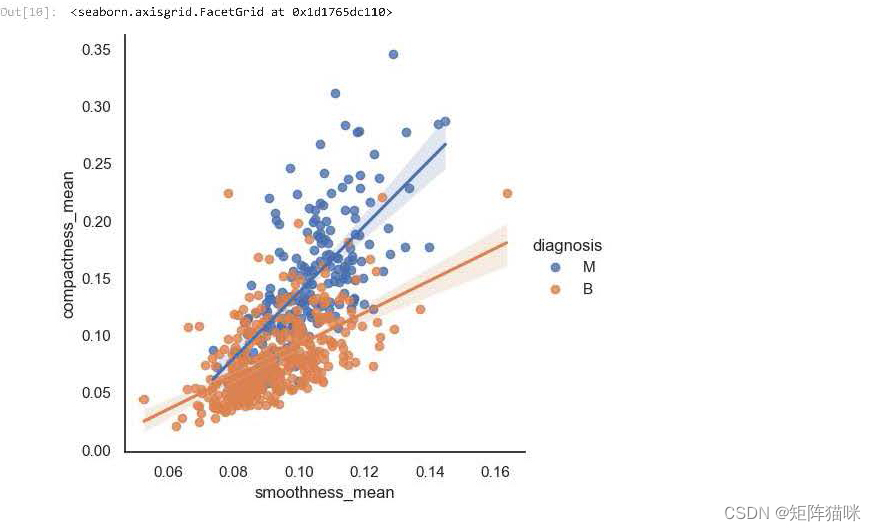
sns.lmplot(x ='smoothness_mean', y = 'compactness_mean',
data = df, hue = 'diagnosis')
3. 数据建模(KNeighborsClassifier)
3.1 数据准备(拆分为训练集和测试集))
X_train, X_val,\
Y_train, Y_val = train_test_split(features, target,
test_size=0.2,
random_state=10)
X_train.shape, X_val.shape
输出
((455, 30), (114, 30))
3.2 模型建立(kNN Classifier)
首先计算不同“k”值的模型性能
# 定义K值的范围
k_range = range(1, 31) # 从1到30
# 存储不同K值对应的性能评估分数
scores = []
# 遍历不同的K值
for k in k_range:
knn_classifier = KNeighborsClassifier(n_neighbors=k)
scores.append(cross_val_score(knn_classifier, features, target, cv=5).mean())
# 找到性能评估分数最高的K值
best_k = k_range[scores.index(max(scores))]
best_s = max(scores)
print(f"The best K for KNN is: {best_k}")
print(f"The best Score for KNN is: {best_s}")
输出
The best K for KNN is: 14
The best Score for KNN is: 0.935010091600683
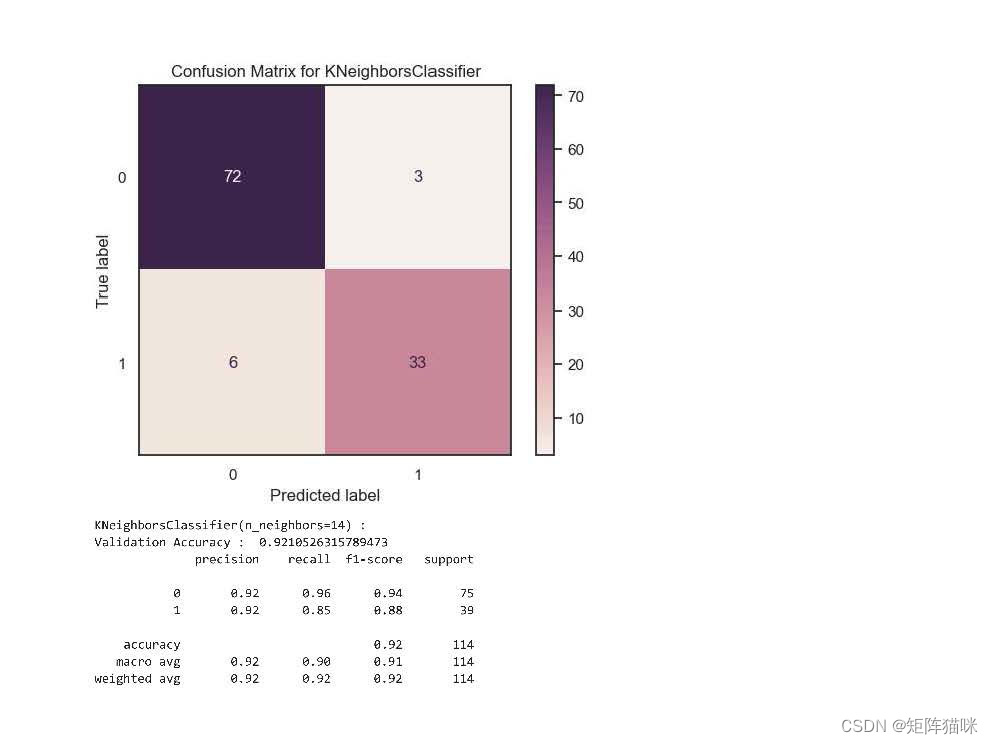
3.3 模型评估
计算混淆矩阵与模型评估
models = KNeighborsClassifier(n_neighbors = best_k)
models.fit(X_train, Y_train)
# 在验证集上进行预测
val_preds = models.predict(X_val)
# 计算混淆矩阵
cm = confusion_matrix(Y_val, val_preds)
# 显示混淆矩阵
metrics.ConfusionMatrixDisplay.from_estimator(
models, X_val, Y_val, cmap=sns.cubehelix_palette(dark=.20, light=.95, as_cmap=True))
plt.title(f'Confusion Matrix for {models.__class__.__name__}')
plt.show()
print(f'{models} : ')
print('Validation Accuracy : ', accuracy_score(Y_val, val_preds))
print(metrics.classification_report(Y_val, models.predict(X_val)))
4. 总结
从上述准确度来看,我们可以看出基于KNN和交叉验证的乳腺癌诊断预测,并没有上篇章节所使用的XGBClassifier在验证数据上的准确率表现更好。若想在此模型上提高准确度,可以借助PCA进行深度探索,以达到理想效果。