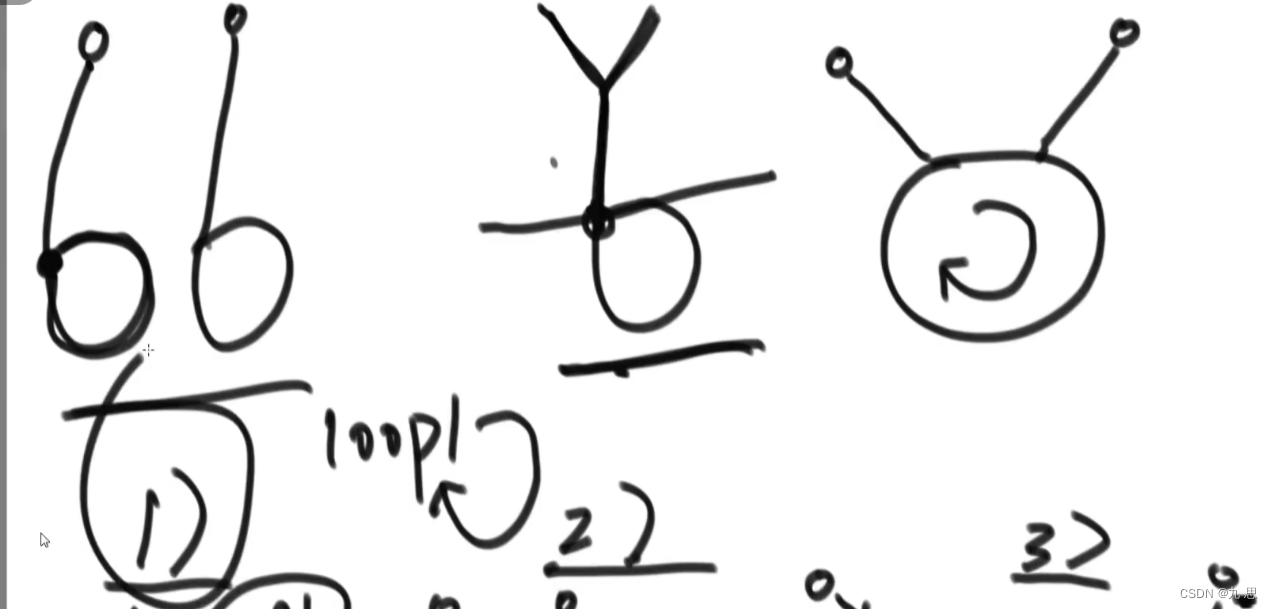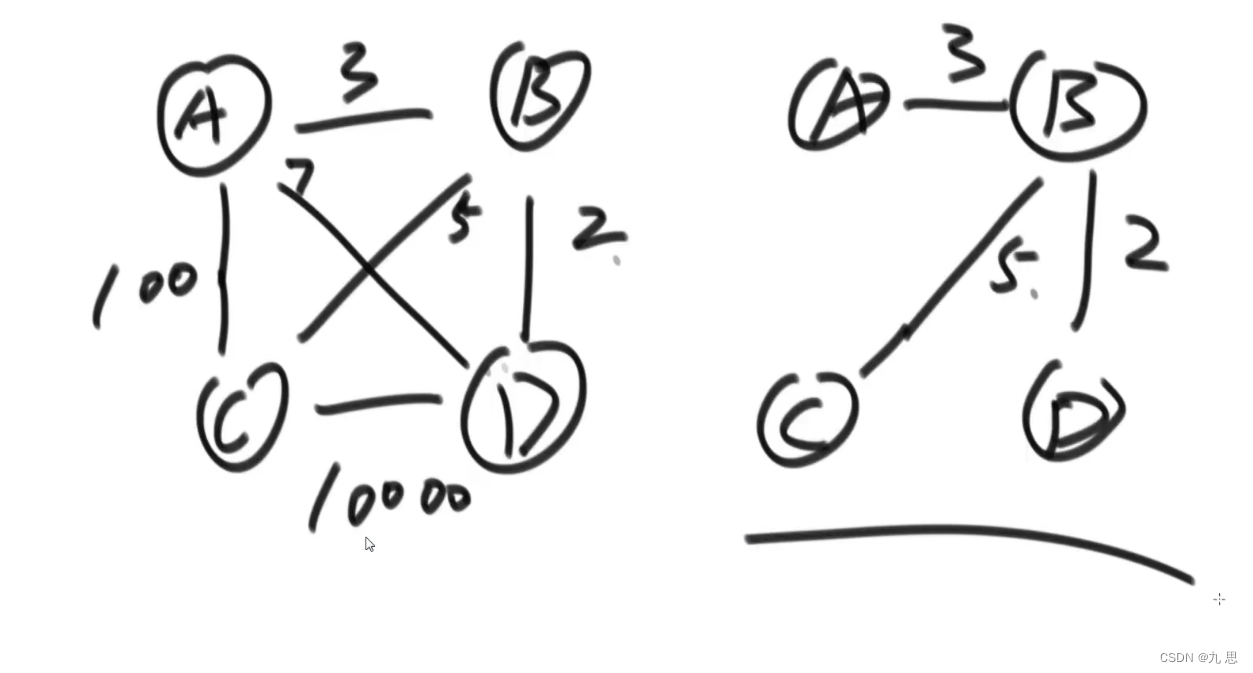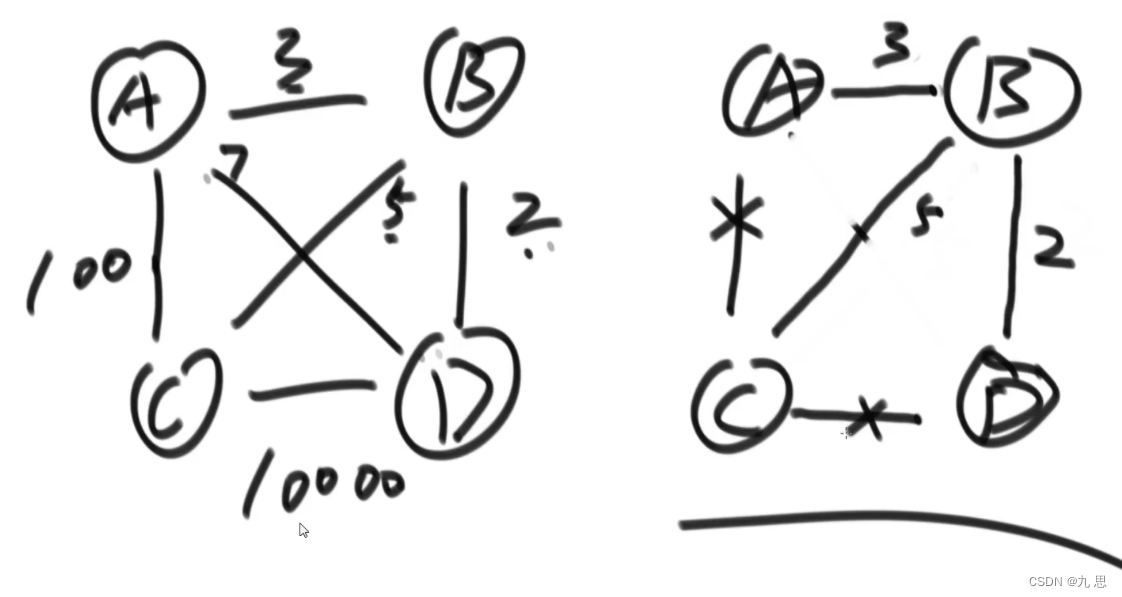基础01(复杂度、基本排序)

认识复杂度和简单排序算法

时间复杂度

big O 即 O(f(n))

常数操作的数量写出来，不要低阶项，只要最高项，并且不要最高项的系数

一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。比如查询数组、作比较、加减乘除、数组中交换位置等

额外空间复杂度

除了储存题目条件外的空间占用，如果只用固定数量的储存空间就能解决问题，不随N变化，那就是常数级O(1)

异或运算

相同为0，不同为1，也可以理解为无进位相加。

异或的性质

1. 0 ^ N = N , N ^ N = 0
2. 异或运算满足交换律和结合律
3. 同一批数异或在一起，结果与谁先异或谁后异或无关

两数交换的另一种写法，但实际上这种方式没一般方法快，而且如果两个数的内存地址一样，会把他们抹成0：

static void fun1(int[] arr,int i,int j){
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
}

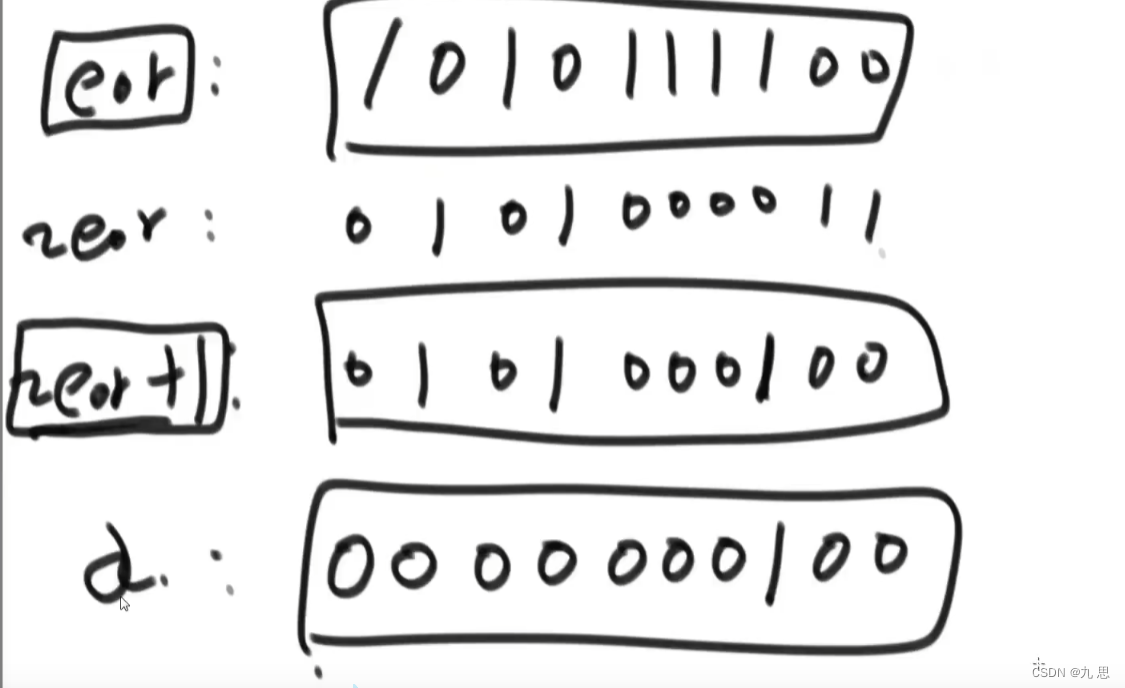
提取出一个二进制数从右往左第一个1的方法：

设该数为a，

int right = a & (~ a + 1)

下图中right就等于4

应用

地址：

一个数出现奇数次__牛客网 (nowcoder.com)

两个数出现了奇数次__牛客网 (nowcoder.com)

（1）一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这一个数？

（2）一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到这两个数？

解答：

（1）由异或的性质得知：偶数个相同数字互相异或得到的结果为0，所以把0与所有数字相异或，所有的偶数出现的数字异或结果为0，剩下的奇数个数字和0异或还是其本身

int main() {
    int n;cin>>n;
    int a[n];
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int ero = 0;
    for(int i=0;i<n;i++){
        ero^=a[i];
    }
    cout<<ero;
    return 0;
} 

（2）假设两个奇数出现的数字分别为a和b。先用0异或所有的数字，结果就是a^b的值，因为a ！= b，则肯定二进制中至少有一位置的数字，一个是0，一个是1，那么根据这个差别，把所有数字分为两种类型，一个是对应位置是1的，一个是0的。然后用0异或所有的该位置上数字为0的，得出来的结果是a或者b，之前已经算出来a^{b的结果，用这个结果去异或这个a或者b，得出的结果就是另一个数字。从这里也可以**总结出一个结论，假设a}b=c,则也有a=b^c**;

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin>>n;
    int a[n];
    int e1 = 0;
    for(int i=0;i<n;i++){
        cin>>a[i];
        e1^=a[i];
    }
    int rightOne = e1 & (~e1 + 1);//提取出一个数最右边的1
    int e2 = 0;
    for(int i=0;i<n;i++){
        if((a[i] & rightOne) == rightOne){ //rightOne除了最右边的1，其余都是0，这一步可以过滤出来最右一位等于1的数字
            e2^=a[i];
        }
    }
    int res1=e2;
    int res2=e1 ^ e2;
    cout<<(res1<res2?res1:res2)<<' '<<(res1<res2?res2:res1);
} 

二分法的详解与扩展

1）在一个有序数组中，找某个数是否存在 。普通二分，找到目标数字就返回

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) { //注意判断条件
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

2）在一个有序数组中，找>=某个数最左侧的位置 。找到大于等于某个数的值不算结束，还要继续向左边二分，直到二分到最后一个数字。相对与（1）修改了while条件，while结束后left和right相等代表查询到中间边界

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int l = 1;
        int r = n;
        int mid = -1;
        while (l<r){
            mid = l + ((r-l)>>1);
            if(isBadVersion(mid)){
                r = mid;
            }else{
                l = mid + 1;
            }
        }
        return l;
       
    }
}

3）局部最小值问题 。题目前提条件是：相邻的数字不相等。见下图。可以理解为极值问题，让我们找到至少一个极值。如果0位置的右边比它大，那0就是局部最小值；同理，如果N-1位置的左边相邻比它大，那么N-1也是一个局部最小值。如果他们都不是最小值，那么，两边的趋势都是向下走的，他们中间肯定有一个地方存在极小值。于是我们二分，查找（N-1）/2 位置的数字，如果该数字两边的值都比它大，那么他就是局部最小值。反之，如果他比某一个方向相邻的数字大，那么它的趋势就会朝着这个方向向下，那么就形成了和上一步相同的情况，如此查找，直到找到局部最小值。

易错：加减乘除优先级大于位运算，比较运算符优先级小于位运算。在使用位运算的时候记得带好小括号

对数器的概念和使用

不用OJ来评测题目对不对，我们用自己做出来的对数器来判断题目对不对。

1. 假如我们想到了一个方法a来解决问题，但是不确定能不能过OJ，于是我们想出来另一个方法b来解决这个问题，方法b一般是实现简单并且时间复杂度不低，比如暴力，我们给这两个方法里传入相同的大量测试数据，如果两个方法返回的结果都是正确的，那么说明方法a和方法b都是正确的。如果有某一个方法返回的结果是错误的，一般就是方法a错，那就说明我们方法a大概率不能通过OJ，这样就验证了方法是不能通过OJ的。
2. 如何生成大量的测试数据？

// maxSize： 最多生成多少个数据，随机的   maxValue： 生成数字的最大值 ,生成数字将在 [0,maxValue) 范围内。
public static int[] generateRandomArray(int maxSize, int maxValue) {
    int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; //数组长度随机 [0,maxSize]
    for (int i = 0; i < arr.length; i++) {
        arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
        //两个随机值相减，值范围[0,maxValue]
    }
    return arr;
}

/*
Math.random() 				返回[0,1) 内所有的小数
Math.random()*N 			返回[0,N) 内所有的小数
(int)(Math.random()*N) 		返回[0,N-1] 内所有整数
*/

3. 把生成的数组再复制一份，总共两份，分别让两个方法处理这两个数组。

public static int[] copyArray(int[] arr) {
		if (arr == null) {
			return null;
		}
		int[] res = new int[arr.length];
		for (int i = 0; i < arr.length; i++) { 
			res[i] = arr[i];
		}
		return res;
	}

4. 算法流程

public static void main(String[] args) {
		int testTime = 500000; //测试次数
		int maxSize = 100;
		int maxValue = 100;
		boolean succeed = true;
		for (int i = 0; i < testTime; i++) {
			int[] arr1 = generateRandomArray(maxSize, maxValue); //生成数组
			int[] arr2 = copyArray(arr1); //复制数组
			insertionSort(arr1); //测试方法a
			comparator(arr2); //测试方法b
			if (!isEqual(arr1, arr2)) { //如果两个数组相等,isEquel实现在下边
				succeed = false;
				break;
			}
		}
		System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}


// isEqual()
	public static boolean isEqual(int[] arr1, int[] arr2) {
		if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
			return false;
		}
		if (arr1 == null && arr2 == null) {
			return true;
		}
		if (arr1.length != arr2.length) {
			return false;
		}
		for (int i = 0; i < arr1.length; i++) {
			if (arr1[i] != arr2[i]) {
				return false;
			}
		}
		return true;
	}

一些基本的排序算法

选择排序、冒泡排序、插入排序–>时间复杂度O(N^2)，额外空间复杂度O(1)

递归行为时间复杂度的估算

master公式：T(N) = a*T(N/b) + O(N^d）

a表示递归拆分成了几个相同的子递归；

N/b 代表子问题的数据规模，如果拆分成相同的两部分，那么b就是2;

N^d 代表除去递归核心步骤，其他代码执行需要的时间复杂度，如果其他代码很少，不随N变化，那么N^d就是1,d就是0；

求出a，b，d的值，然后代入下面公式，即可估算出递归算法的时间复杂度

1. log(b,a) > d -> 复杂度为O(N^log(b,a))
2. log(b,a) = d -> 复杂度为O(N^d * logN)
3. log(b,a) < d -> 复杂度为O(N^d)

log(b,a)代表log以b为底，a的对数

基础02(排序)

归并排序

1）整体就是一个简单递归，左边排好序、右边排好序、然后merge，让其整体有序。左边和右边排序依然是递归

2）让其整体有序的过程里用了外排序方法

3）利用master公式来求解时间复杂度

4）时间复杂度O(N*logN)，额外空间复杂度O(N)

代码见：Code01_MergeSort

小和问题和逆序对问题

1. 小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组 的小和。求一个数组 的小和。 例子:[1,3,4,2,5] 1左边比1小的数，没有; 3左边比3小的数，1; 4左 边比4小的数，1、3; 2左边比2小的数，1; 5左边比5小的数，1、3、4、 2; 所以小和为1+1+3+1+1+3+4+2=16

这道题用归并排序的思想可以解决。首先，求小和只要从每个数开始向他右边查，看有几个大于他的数，就把自己乘几，把结果依次相加就得出小和。那么在归并排序中，每次归并时，对于每个左边的数，看右边部分有几个大于他的数，就把大于他的数的数量乘以他，依次归并后得出来小和结果。并且，右边大于左边数的数量可以根据下标差来计算，因为右边是有序的，只要发现第一个大于他的数，那么后边就都是大于他的数，用最右边的下标减去第一个大于他的下标。

2. 逆序对问题

在一个数组中，左边的数如果比右边的数大，则折两个数 构成一个逆序对，请打印所有逆序 对

逆序对问题和小和问题正好相反，但思路一模一样，只要在归并时判断右边小于左边每个数的个数，然后乘以他就行了。

荷兰国旗问题

问题一

给定一个数组arr，和一个数num，请把小于等于num的数放在数 组的左边，大于num的 数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)

问题二(荷兰国旗问题)

给定一个数组arr，和一个数num，请把小于num的数放在数组的 左边，等于num的数放 在数组的中间，大于num的数放在数组的 右边。要求额外空间复杂度O(1)，时间复杂度 O(N)

快速排序

不改进的快速排序：

1）把数组范围中的最后一个数作为划分值，然后把数组通过荷兰国旗问题分成三个部分：

左侧<划分值、中间==划分值、右侧>划分值

2）对左侧范围和右侧范围，递归执行

分析：

1）划分值越靠近两侧，复杂度越高；划分值越靠近中间，复杂度越低

2）可以轻而易举的举出最差的例子，所以不改进的快速排序时间复杂度为O(N^2)

随机快速排序（改进的快速排序）

1）在数组范围中，等概率随机选一个数作为划分值，然后把数组分成三个部分： 左侧<划分值、中间==划分值、右侧>划分值

2）对左侧范围和右侧范围，递归执行

3）时间复杂度为O(N*logN)；空间复杂度是O(logN)。

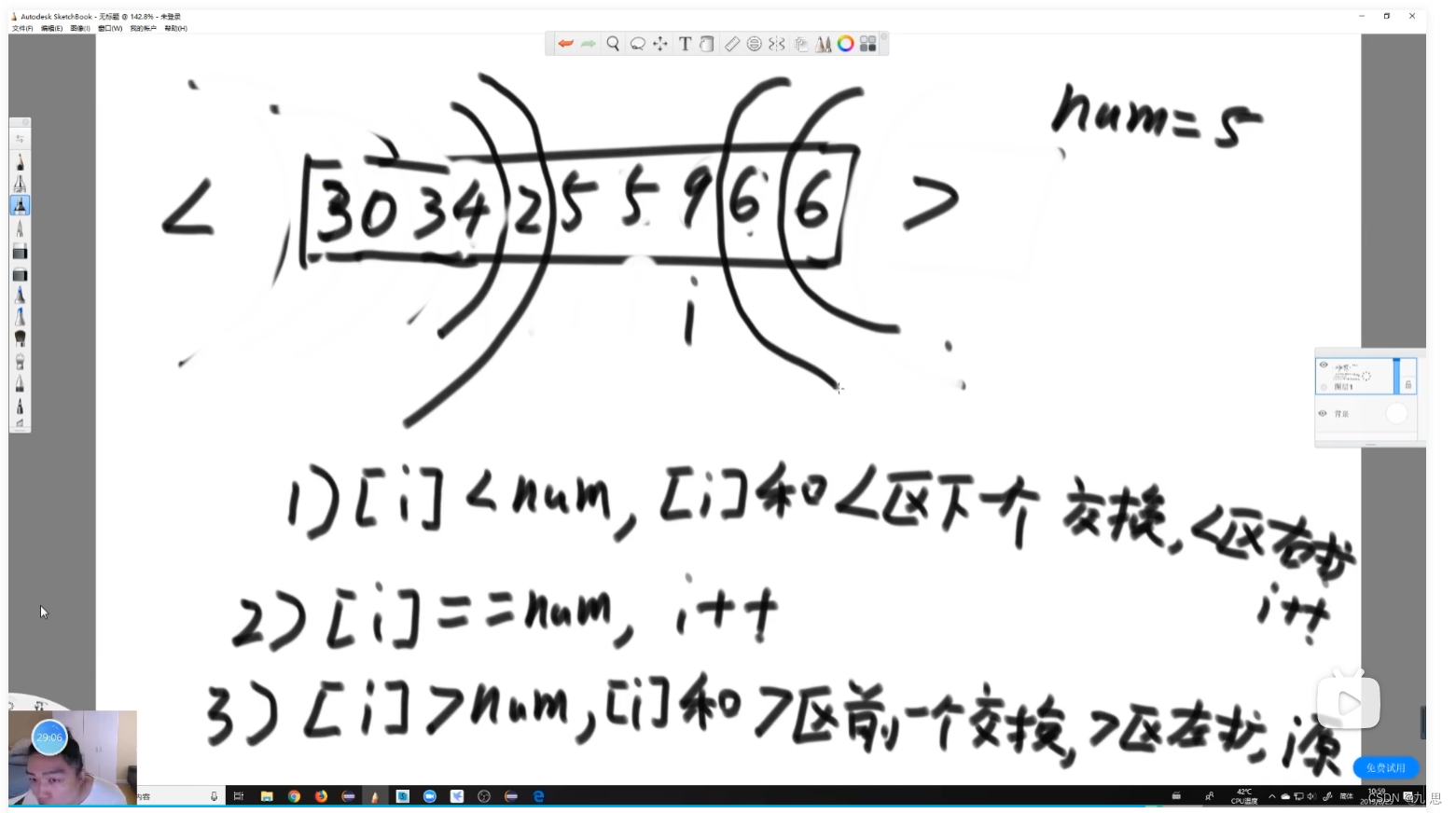
partition过程：

//使当前区域分为小于、等于、大于三个区域的方法
	public static int[] partition(int[] arr, int l, int r) {
		int less = l - 1;//小于区域的有右边界
		int more = r;//大于区域的左边界
		//从左到右依次遍历遇到大于选定值的数，让它和小于区域的下一个位置的数做交换，同时小于区域往右扩；遇到等于的数字，不管；遇到大于的数字，让他和大于区域的左边一个数字和它做交换，同时大于区域往左扩
		//arr
		//arr[r]代表选定最右侧数字为选定值，让每个数和他进行对比
		while (l < more) {
			if (arr[l] < arr[r]) {
				swap(arr, ++less, l++);
			} else if (arr[l] > arr[r]) {
				swap(arr, --more, l);
			} else {
				l++;
			}
		}
		swap(arr, more, r);
		return new int[] { less + 1, more };
	}

快排对空间的消耗主要体现在递归造成的栈空间的使用，好情况下每次选择的数都是中点，空间复杂度为logN,最差情况下选的都是最后一个数为N。每次递归都需要记录选出中点的位置，相当于求二叉树的高度。每次左边quicksort完，记录左边中点的空间可以释放，然后让右边使用，所以是logn级别

TopK问题

最优解是基于快排的快速选择算法

TopK问题，快速选择算法是最优解，其是在快排基础上做出的优化算法
参考：https://zhuanlan.zhihu.com/p/64627590
每次随机找一个值作为pivot，也就是中间值，比如从第一个数字开始找。下标为0的数字为pivot。
然后进行快排，让小于pivot的数字都在左边，大于pivot的数字都在右边。之后判断大于pivot的数字的个数，我们是要找到第k个大的数，
那也就是要保证在整个数组里大于这个数的要有k-1个，如果pivot右边的数字个数不是k-1，那就说明我们这个pivot不是第k个大的数。
但是至少可以保证目标值肯定在当前pivot的右边，那我们直接对右边的数字进行循环，设置右边数字第一个为pivot，
直到找到一个pivot，他右边数字有k-1个，这就是TopK。

快速选择算法就是为了避免进行多余的操作，比如快排思路，我们把Top1、Top2、Top3…TopK…TopN都找了出来，这是多余的操作。
在堆排序思路中，虽然维护堆的大小为k，但是还是找到了多余的Top1、Top2、Top3…Topk-1

堆

1,堆结构就是用数组实现的完全二叉树结构
2,完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
3,完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
4,堆结构的heapInsert与heapify操作
5,堆结构的增大和减少
6,优先级队列结构，不是队列，就是堆结构

7，大根堆小根堆一般用来维护整个数组的最大值或者最小值。每次剔除维护出来的最大值，然后添加到辅助数组的后面，就把数组进行了堆排序。

8.Java中小根堆、大根堆结构怎么实现？

PriorityQueue<Integer>heap = new PriorityQueue<>();//如果不传入构造参数，默认是小根堆。
heap.add(8);
heap.add(4);
heap.add(4);
heap.add(9);
heap.add(10);
heap.add(3);
while (!heap.isEmpty(){
    System.out.println(heap.poll());
}
//打印结果:3 4 4 8 9 10

9.Java中堆结构扩容花费的时间复杂度？

每次扩容会扩大到当前堆大小的两倍，2,4,8,16…,容易知道对于N个数，扩容的次数是logN级别的，而且每次扩容后还要把原来堆的数复制到新堆里，这个时间复杂度是N级别，相乘就是O(N*logN),但是把这个时间复杂度均摊到每个数，就是O(logN),所以说扩容带来的复杂度影响不大。

10.系统提供的堆结构是一个黑盒，并且提供的方法比较少，比如修改堆中的某个数并且重新维护成大根堆，这个系统不支持，或者说维护代价很大，只能手写。所以说某些情况下我们需要手写堆结构。

堆排序

heapInsert：让整个数组都变成大根堆结构，建立堆的过程:

​ 情况一：用户一个一个输入数字，我们一个一个heapInsert,利用从上到下的方法，建立大根堆，加一个数需要比较树的高度次，O(logN),当0到i-1加入一个数需要比较log（I-1）次；N个数需要log1+log2+…+log（N-1）=O(N)

​ 情况二：用户一下子给了一个数组的值，我们从下到上地执行heapify方法，时间复杂度为O(N) 。这种情况，至少在步骤一这里，比情况一快一点。

两种情况的代码：

//情况一：
for (int i=0;i<arr.length;i++){//O(N)
	heapInsert(arr,i);//0(logN)
}
//情况二：
for(int i=arr.length -1;i>=0;i--){
	heapify(arr,i,arr.length);
}

heapify：假设数组中一个值变小了，重新调整为大根堆的过程

​ heapsize可以用来控制heapify的结束，当孩子的下标大于heapsize的时候可以判断堆里没有其他孩子了，而不是根据数组的大小判断堆的结束

堆排序：

（1）让数组变为大根堆（heapinsert）；
（2）让最后一位和堆顶交换，堆大小减一（保存最大值）
（3）再重新变为大根堆，相当于把堆顶元素变小再重排（heapify）
（4）直到堆大小为0停止。

（每次调整堆后都会得出目前堆中的最大值，依次把最大值放在help数组的尾部，就得出降序的排序结果）

时间复杂度：

O(N*logN)，不考虑建立堆的过程，每次排序logN，排N个。

ps:

1. 当把堆中的某个数改变后，不知道他是变大还是变小，我们可以直接调用heapInsert或者heapify，这两个方法肯定会执行其中一个，如果heapInsert能执行说明数字变大，如果反之说明数字变小，而且方法执行后堆会重新变成大根堆

代码：

	public static void heapSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			heapInsert(arr, i);
		}
		int size = arr.length;
		swap(arr, 0, --size);
		while (size > 0) {
			heapify(arr, 0, size);
			swap(arr, 0, --size);
		}
	}

	public static void heapInsert(int[] arr, int index) {
		while (arr[index] > arr[(index - 1) / 2]) {
			swap(arr, index, (index - 1) /2);
			index = (index - 1)/2 ;
		}
	}

	public static void heapify(int[] arr, int index, int size) {
		int left = index * 2 + 1;
		while (left < size) {
			int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
			largest = arr[largest] > arr[index] ? largest : index;
			if (largest == index) {
				break;
			}
			swap(arr, largest, index);
			index = largest;
			left = index * 2 + 1;
		}
	}

堆排序扩展题目

已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。

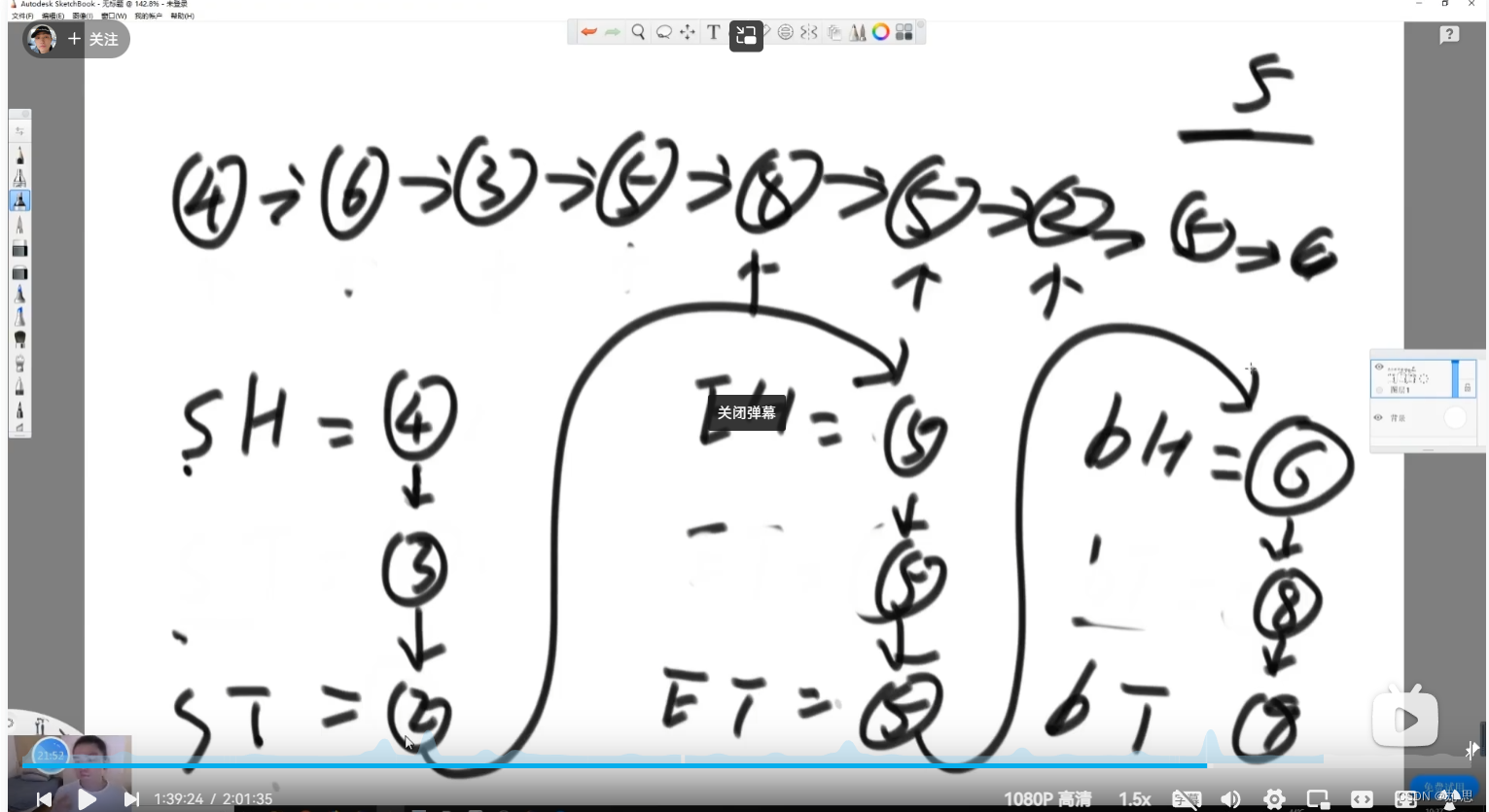
解题思路：假设这个数组是升序，那么整个数组的最小值肯定是在前k+1个数中选择出来的，因为即使最小值原来在第k+1个，最小值排序后就在第一个，不可能在k+2及其以后，因为如果在k+2及其以后，他再移动到第一个就需要k+1步，不符合规定，所以当前数组的最小值总是在前K+1个里得到。那么维护一个大小为K+1的小根堆，每次取出小根堆的根，然后放到辅助数组的尾部，循环，便得到了升序数组。

每次维护小根堆需要O(logk)，维护N次，时间复杂度就是O(N*logk)

为什么维护小根堆数组时间复杂度不是O(N)?

因为k是固定的，每次维护小根堆只需要固定的步数也就是logk。之前算出来的那个O(N)是因为用户给的数字不是有限的，才需要N/2+N/42+N/83……，这里是固定有限的logk

基础03(排序、比较器、排序总结)

比较器

1）比较器的实质就是重载比较运算符

2）比较器可以很好的应用在特殊标准的排序上

3）比较器可以很好的应用在根据特殊标准排序的结构上

如何使用？就是实现Comparator接口中的compare方法，并把实现类传入到Arrays.sort(students, new IdAscendingComparator())方法里即可。

public static class Student {
		public String name;
		public int id;
		public int age;

		public Student(String name, int id, int age) {
			this.name = name;
			this.id = id;
			this.age = age;
		}
	}
public static class IdAscendingComparator implements Comparator<Student> {
		//返回负数的时候，第一个参数排在前面
		//返回正数的时候，第二个参数排在前面
		//返回0的时候，谁在前面无所谓
		@Override
		public int compare(Student o1, Student o2) {
			return o1.id - o2.id;
		}

	}

Arrays.sort(students, new IdAscendingComparator());

比较器在PriorityQueue堆结构中的使用

PriorityQueue<Integer> heap = new PriorityQueue<>(new AComp());

public static class AComp implements Comparator<Integer>{
    //如果返回负数，认为第一个参数应该放在上面
    //如果返回正数，认为第二个参数应该放在上面
    //如果返回0，认为谁放上面都行
    @Override
    public int compare(Integer arg0,Integer arg1){
        return arg1 - arg0;
    }
}

比较器AComp，用第二个参数减第一个参数，如果是负数，需要把第一个参数放上面，也就是把大的放在上面。这样PriorityQueue就成了大根堆。

桶排序思想下的排序

分析：

1)桶排序思想下的排序都是不基于比较的排序

2)时间复杂度为O(N)，额外空间复杂度O(N)

3)应用范围有限，需要样本的数据状况满足桶的划分。比如计数排序，必须要提前知道数值范围最大是多少，从而规定数组大小，而且如果数组最大值太大导致数组太大，并且数值命中率降低，效率非常慢。同样的，对于基数排序，如果数组的数不属于进制数字（十进制等等），那么排序就无法进行。

计数排序

算法描述：加入有一些数字，这些数字都是200以内的，那我就可以声明一个大小为200的数组，然后遍历数字，如果数字是10那就在下标为10的位置上+1，每个数字都是如此。遍历完成后，从0开始把每个位置上不为0的数字依次写出来，比如8的位置上是5，那就在排序队列中添加5个8，依次遍历完成后，就可以得出排序结果。具体代码参考CountSort

基数排序

算法描述：基数排序需要让每个数字的位数统一，如果最大值是100，那么二位数的前面就要加一个0。先把数字根据个位分类，分别放到0-9这10个桶子里，个位是1的放在1桶子里，是2的放在2桶子里。这个桶子是队列结构，然后从0桶开始依次把数取出来（遵循FIFO），然后进行第二轮，根据十位分类，也是根据数字分类，然后循环。最大数有几位，就循环几次进桶出桶的操作。

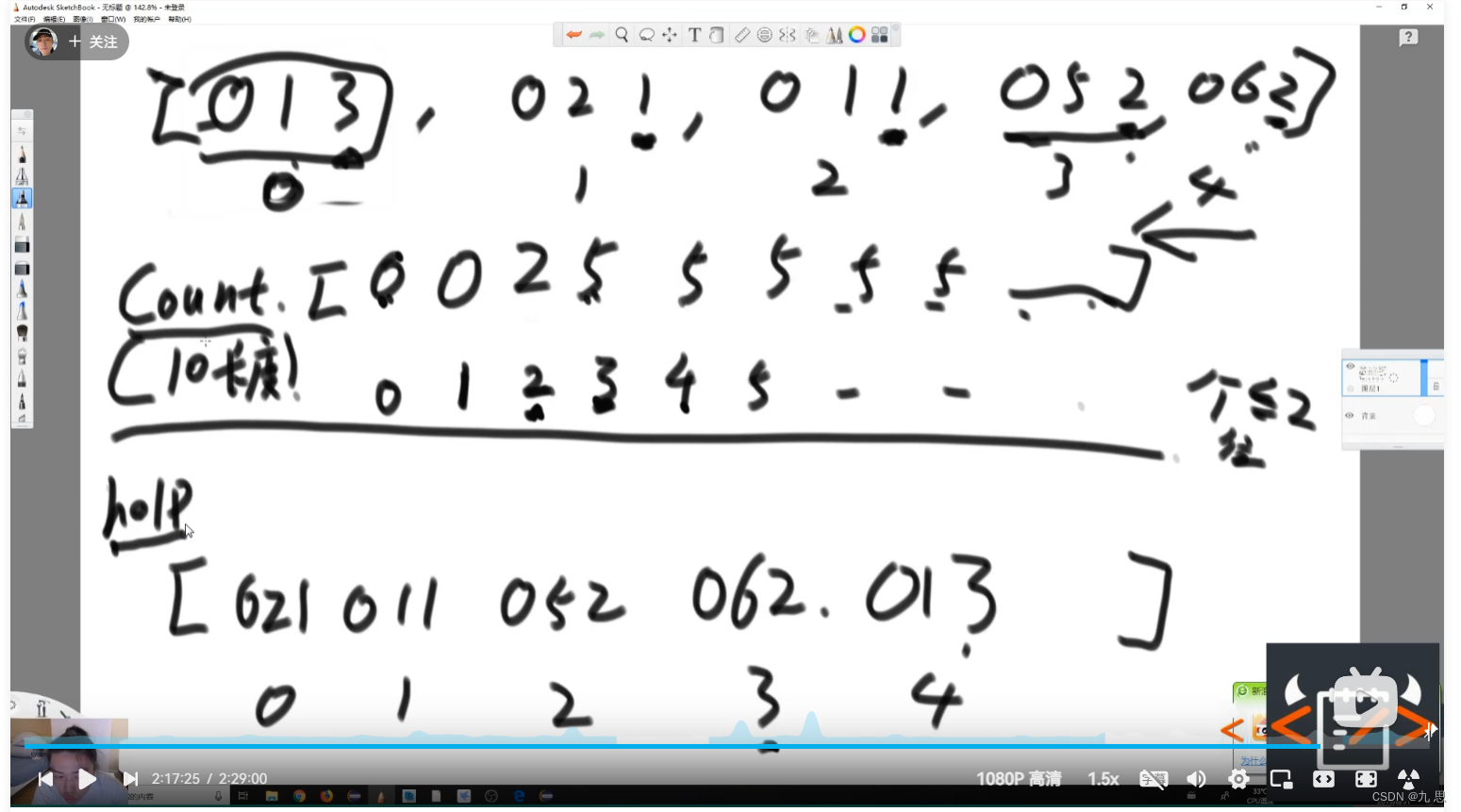
具体代码参照RadixSort，需要注意的是，代码对进桶和出桶操作进行了优化，视频在P5的2:10:48有详解，图片在下方图1和图2。大概流程是，用大小为10的Count数组，先统计个位上为0-9的分别有几个，然后从下标1开始设置该位置上的数为自己的前一位加上自己，相当于求了一个前缀和。求完之后，比如下标为2的位置，值为4，代表总共有4个数，他的个位小于等于2，然后我们从需要排序的数组的最右侧开始，判断每一个数字应该放在help数组的哪个位置。比如最后一个数字是062，那么他就应该放在第四个位置上，也就是下标为3的位置，放进去之后，需要把下标为2的数字-1，变成3，这就代表现在还有3个数字小于等于2。然后往左看，052，因为小于等于2目前只有3个，所以把052放在第3位，然后依次进行判断。判断结束之后，算是根据个位大小拍完了序，然后用help数组里的内容替换原数组，下一步是按照十位进行排序。需要注意的是，052和062谁在左在右都无所谓，因为现在排序排的是个位的数字，十位排序会在下一步进行，我们只需要按照从右到左依次放入help数组就行。

希尔排序（了解）

分组排序（多次分组大小递减）后插入排序。先分组排序后，数组近乎有序，这种情况下插入排序插入次数减少，时间复杂度降低。

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

排序算法的稳定性及其汇总

稳定性并不是指不同数据情况下时间复杂度会变化，而是指相同数值的数字在排序之后他们的先后顺序不变，这在数字这种简单数据下可能没什么意义，但是在复杂数据类型的排序是很重要的性质。比如对商城商品进行价格升序排序后再进行好评率排序，如果算法稳定，价格顺序不会随好评率变化，那么挑选出来的商品就是物美价廉的商品。

不具备稳定性的排序： 选择排序、快速排序、堆排序

1. 选择排序因为要选出最大值放在最后，在交换数字的时候就容易改变同数值数字顺序。
2. 快速排序在找到小于中间值后需要把这个值和“小于数组”的下一个数字进行交换，这个过程也会导致不稳定。
3. 堆排序在进行insert的过程，交换父子数字时会造成不稳定。

具备稳定性的排序： 冒泡排序、插入排序、归并排序、一切桶排序思想下的排序

冒泡排序中只会交换相邻的不同数值的数字，只要保证不交换相等数字就行，遇到相等数字直接跳过就行。

插入排序和冒泡一样，只要保证遇到相等数字时不要交换数字就能保证稳定性。

归并排序在merge时遇到右边有数字和左边数字相同的时候，只要保证先把左边的放到排序数组中就行，先左边后右边。注意，在小和问题中，不能保证稳定性。

桶排序这种不基于比较的算法，相同数值的数字存到相同的桶中，先进先出不会打乱顺序。

目前没有找到时间复杂度O(N*logN)，额外空间复杂度O(1)，又稳定的排序。

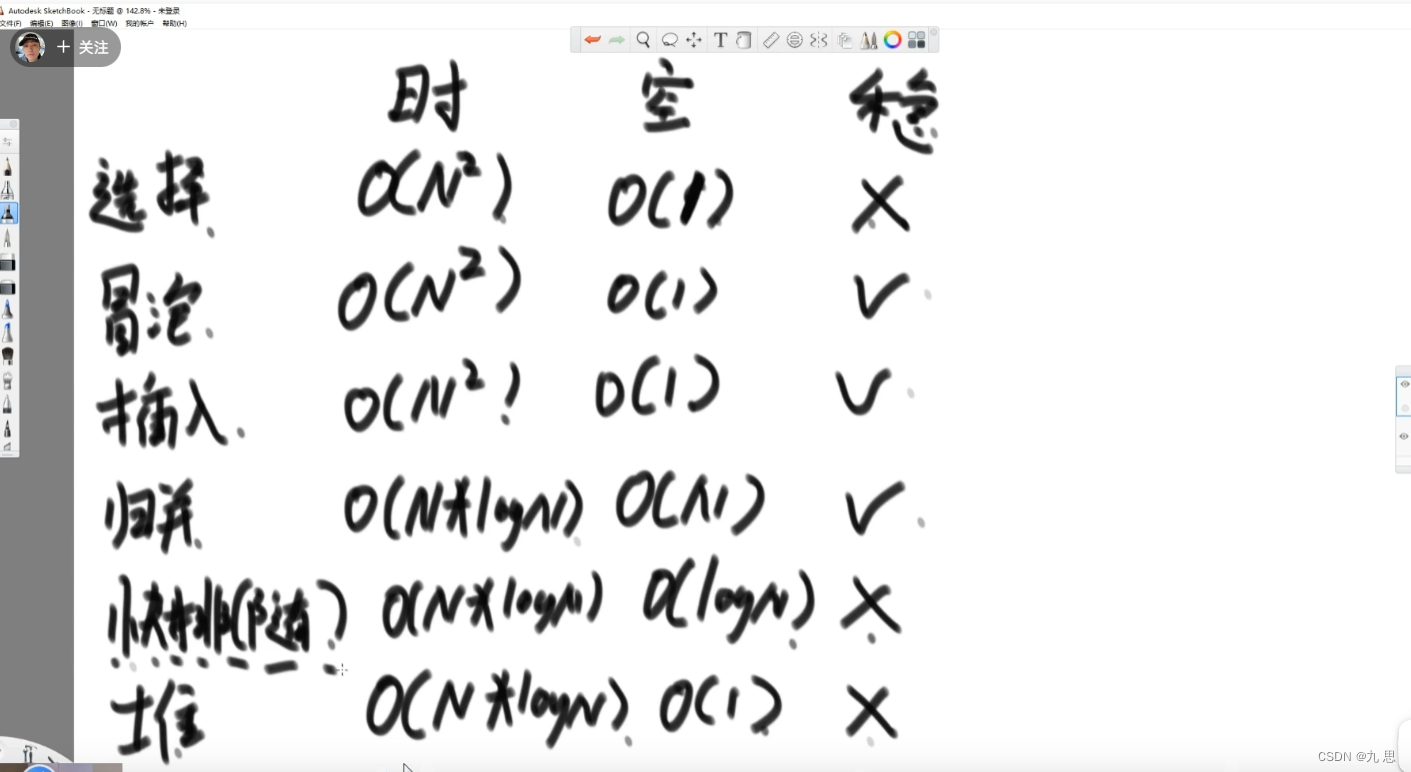
各种排序算法的时、空、稳

在一般使用中能用快排的尽量用快排，堆排序一般在对空间复杂度要求很高、空间很小的情况下使用，归并排序在追求稳定性时使用

常见的坑

1，归并排序的额外空间复杂度可以变成O(1)，但是非常难，不需要掌握，有兴 趣可以搜“归并排序 内部缓存法”

2， “原地归并排序”的帖子都是垃圾，会让归并排序的时间复杂度变成O(N^2)

3，快速排序可以做到稳定性问题，但是非常难，不需要掌握， 可以搜“01 stable sort”

4，所有的改进都不重要，因为目前没有找到时间复杂度O(N*logN)，额外空间复 杂度O(1)，又稳定的排序。

5，有一道题目，是奇数放在数组左边，偶数放在数组右边，还要求原始的相对次序不变，碰到这个问题，可以怼面试官。这道题可以类似于快排，奇数放在左边，偶数放在右边，但是这样会不稳定，如果要保证稳定性，需要步骤很复杂很难，写论文都不一定能搞定，以此反驳面试官。

工程上对排序的改进

1）充分利用O(N*logN)和O(N^2)排序各自的优势

比如，在进行快速排序的过程中，如果发现数据规模很小，那么就可以使用插入排序，虽然插入排序的时间复杂度是O(N2)【在这里对整体时间影响不大】，但是他的空间复杂度为O(1)，省空间。当样本量大的时候，使用快排，时间复杂度低。

Java的Arrays.sort()方法也是根据数据规模和数据情况动态调整排序策略。

2）稳定性的考虑

系统中的sort方法，在对简单数据类型–数字，进行排序的时候，可能会使用快排，因为不用保证稳定性，并且速度很快。但是对复杂数据类型进行排序的时候就很可能会使用归并排序，因为要保证数据稳定性。

基础04(哈希表、有序表、链表)

哈希表的简单介绍

1）哈希表在使用层面上可以理解为一种集合结构

2）如果只有key，没有伴随数据value，可以使用HashSet结构(C++中叫UnOrderedSet)

3）如果既有key，又有伴随数据value，可以使用HashMap结构(C++中叫UnOrderedMap)

4）有无伴随数据，是HashMap和HashSet唯一的区别，底层的实际结构是一回事

5）使用哈希表增(put)、删(remove)、改(put)和查(get)的操作，可以认为时间复杂度为 O(1)，但是常数时间比较大

6）放入哈希表的东西，如果是基础类型，内部按值传递，内存占用就是这个东西的大小

7）放入哈希表的东西，如果不是基础类型，内部按引用传递，内存占用是这个东西内存地址的大小 有关哈希表的原理，将在提升班“与哈希函数有关的数据结构”一章中讲叙原理

有序表的简单介绍

1）有序表在使用层面上可以理解为一种集合结构

2）如果只有key，没有伴随数据value，可以使用TreeSet结构(C++中叫OrderedSet)

3）如果既有key，又有伴随数据value，可以使用TreeMap结构(C++中叫OrderedMap)

4）有无伴随数据，是TreeSet和TreeMap唯一的区别，底层的实际结构是一回事

5）有序表和哈希表的区别是，有序表把key按照顺序组织起来，而哈希表完全不组织

5）红黑树、AVL树、size-balance-tree和跳表等都属于有序表结构，只是底层具体实现 不同

6）放入有序表的东西，如果是基础类型，内部按值传递，内存占用就是这个东西的大小

7）放入有序表的东西，如果不是基础类型，必须提供比较器，内部按引用传递，内存占 用是这个东西内存地址的大小

8）不管是什么底层具体实现，只要是有序表，都有以下固定的基本功能和固定的时间复杂度

有序表的固定操作

1）void put(K key, V value)：将一个（key，value）记录加入到表中，或者将key的记录 更新成value。

2）V get(K key)：根据给定的key，查询value并返回。

3）void remove(K key)：移除key的记录。

4）boolean containsKey(K key)：询问是否有关于key的记录。

5）K firstKey()：返回所有键值的排序结果中，最左（最小）的那个。

6）K lastKey()：返回所有键值的排序结果中，最右（最大）的那个。

7）K floorKey(K key)：如果表中存入过key，返回key；否则返回所有键值的排序结果中， key的前一个。

8）K ceilingKey(K key)：如果表中存入过key，返回key；否则返回所有键值的排序结果中， key的后一个。

以上所有操作时间复杂度都是O(logN)，N为有序表含有的记录数

有关有序表的原理，将在提升班“有序表详解”一章中讲叙原理

反转链表

反转链表需要注意翻转链表的方法需不需要返回头指针，如果返回了头指针，方法外部就遍历反转后的链表

打印两个有序链表的公共部分

这个题目有点类似merge的过程，两个指针分别同时从头部开始，指针指向的的数值较小的先走，然后遇到相等的数值就打印，打印后两个指针同时向右走，当一个指针走到最后打印结束。

面试时链表解题的方法论

1）对于笔试，不用太在乎空间复杂度，一切为了时间复杂度，只要复杂度够低，能过就行

2）对于面试，时间复杂度依然放在第一位，但是一定要找到空间最省的方法。只有这样才能在面试官面前脱颖而出

练题的时候按照笔试的要求和面试的要求分别去练

重要技巧

1）额外数据结构记录（栈、哈希表等）

2）快慢指针。比如在下面判断回文链表时就有用

判断一个链表是否为回文结构

【题目】给定一个单链表的头节点head，请判断该链表是否为回文结构。

【例子】1->2->1，返回true； 1->2->2->1，返回true；15->6->15，返回true； 1->2->3，返回false。

1.0：把整个链表依次放进栈里。此时链表最后面的数字在栈的顶部。让一个指针从链表头部开始，栈顶弹出一个值，和指针的数值进行对比，对比相同则指针前进一步，栈接着弹出一个数进行对比，如果指针走到最后都没有存在不相同的值，那么该链表是回文链表。

2.0：想办法把后一半的链表放进栈里，然后只用对比一半就行。怎么找到链表的中间位置：可以采用快慢指针的方法，快指针一次走两步，慢指针一次走一步，当快指针走到尾部的时候，慢指针就走到了中间。然后把后一半的数字放入栈中，然后比较数字，那么这样只要比较一半就行。这里需要注意，快慢指针的使用在不同情境下可能会有一些不同的要求，可能有的要求快指针走到末尾时慢指针走到中间数字的前一个或者中间两个数字的第一个，等等，需要改变一点点实现方式。

3.0（空间复杂度为1，不依赖其他容器）：让中间的数字指向空，然后让中间后边的所有数字的指向翻转，从两头开始对比，对比完成后，再把后半部分的数字指向变为原来的方向。这样就实现空间复杂度为O(1)的算法，适合在面试时使用。

【例子】如果链表长度为N，时间复杂度达到O(N)，额外空间复杂度达到O(1)。

参考判断回文链表解法的3.0版本。

将单向链表按某值划分成左边小、中间相等、右边大的形式

【题目】给定一个单链表的头节点head，节点的值类型是整型，再给定一个整数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的节点，中间部分都是值等于pivot的节点，右部分都是值大于pivot的节点。

笔试解法：可以申请一个Node类型的数组，把链表里的数字依次放进数组里进行partition，排完之后把数组串成链表。

【进阶】在实现原问题功能的基础上增加如下的要求

【要求】调整后所有小于pivot的节点之间的相对顺序和调整前一样

【要求】调整后所有等于pivot的节点之间的相对顺序和调整前一样

【要求】调整后所有大于pivot的节点之间的相对顺序和调整前一样

【要求】时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

面试解法：只用额外申请6个指针变量就行。这六个指针分别指向小于部分、等于部分和大于部分的头和尾，开始时都是null，然后让一个指针遍历链表，当第一次遇到小于pivot的数字时，把小于部分头指针指向它，并且小于部分尾指针指向它，再次遇到小于部分的数字时，尾指针的next指向这个数字，然后尾指针指向这个数字，如此就可以把小于部分连成一个链表，并且前后顺序不变。当遇到等于数字和大于数字是操作相同。最后形成3个链表，分别是小于等于大于，把这三个链表连起来就排列完成了。注意，在排列的过程中会修改原链表中数字的next指向，不过这些修改无关紧要，因为我们只用看最后连成链表的顺序。在连接三部分的时候需要判断小于部分是不是null的，如果是null就不能直接指向等于部分，否则空指针，这些边界都需要进行判断。具体代码参考：SmallerEqualBigger

复制含有随机指针节点的链表

【题目】一种特殊的单链表节点类描述如下

class Node { 
    int value; 
    Node next; 
    Node rand; 
    Node(int val) { 
    	value = val; 
    } 
} 

rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点 head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。

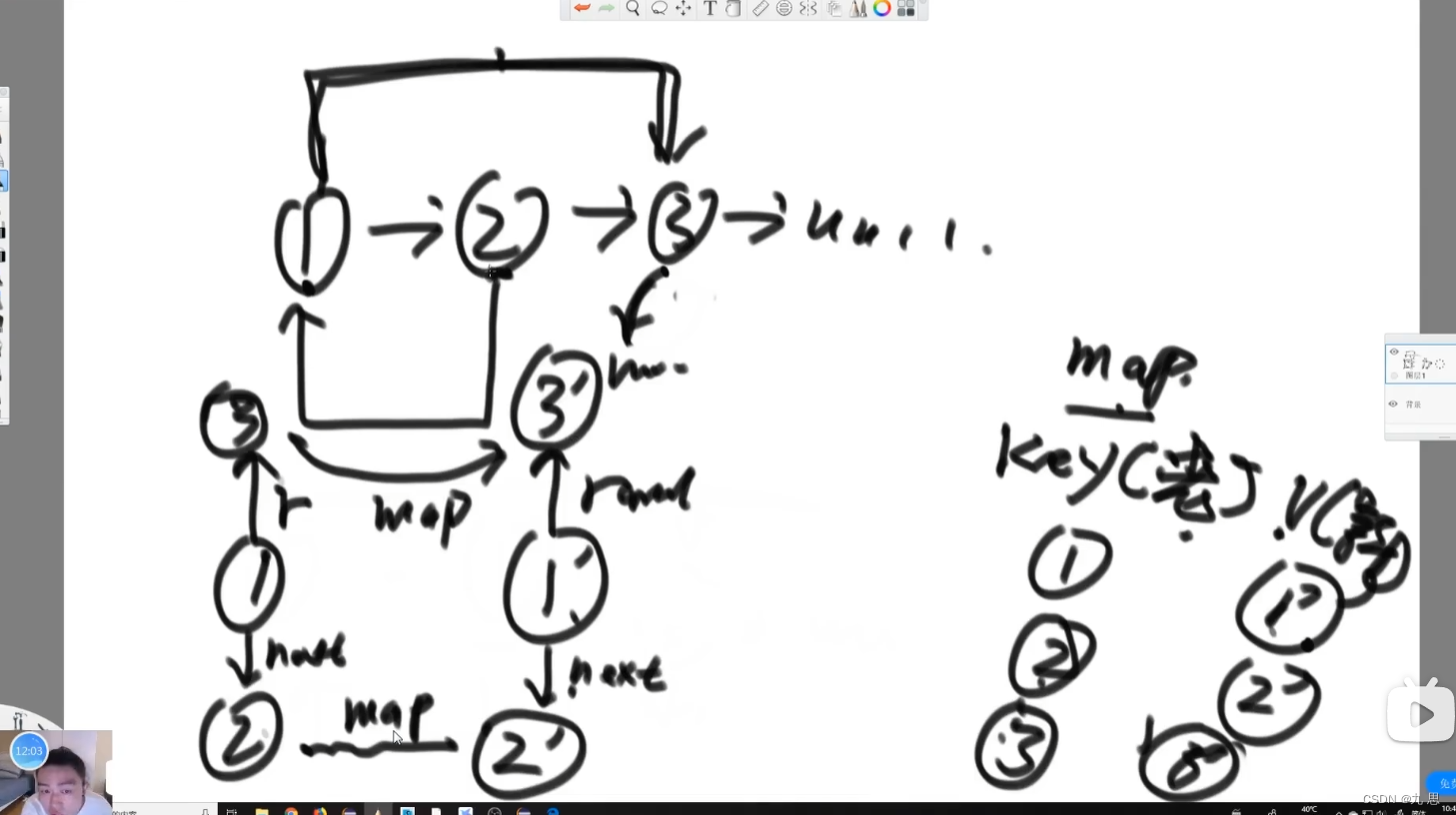
笔试解法：用一个HashMap<Node,Node>,key存放原来链表中的每个节点，对应的value为key的克隆节点，克隆节点只复制value属性。如下图，先看1节点，1节点的next指向2，我们根据key–2查询到2’,然后把1’的next指向2’，判断1的rand指针的指向，然后指向对应的n’，最后返回1’就行，这是新链表的头指针。代码参考CopyListWithRandom。这个写法用到了一个hashmap的空间和存储最终结果的空间，存储最终结果的空间不算额外空间，只剩下一个hashmap的空间，但是空间复杂度不是O(1)级别。

面试写法

【要求】时间复杂度O(N)，额外空间复杂度O(1)：

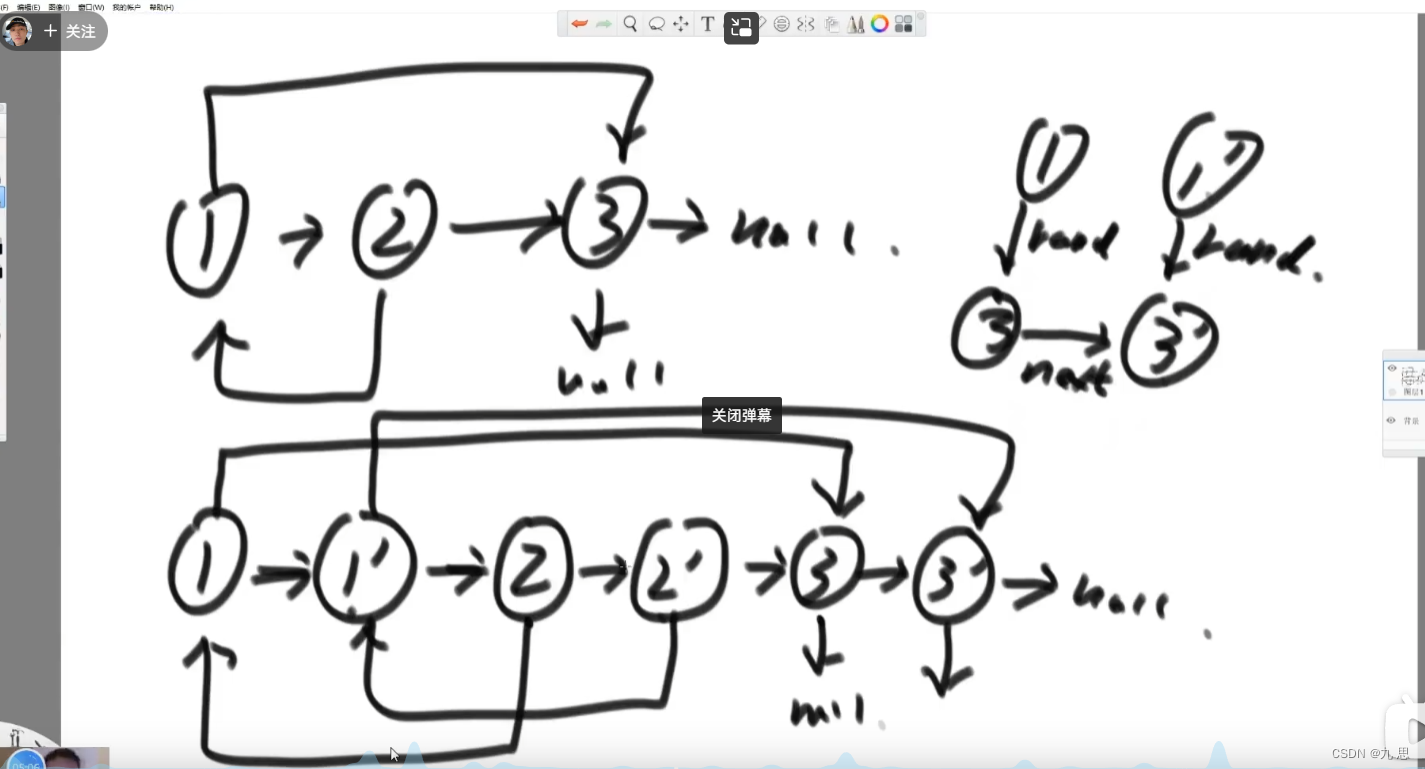
克隆出每个节点，（克隆这些节点所花费的空间不属于额外空间，因为这些空间是用来储存结果的，所以不算在空间复杂度里），让每一个节点的next指向他的克隆节点，克隆节点的next指向原节点的下一个原节点，如下图所示。然后成对的判断，比如1和1’，1’的rand是1的rand的next–3’，让1’指向3’，再处理2、3、4等等，然后再把所有的复制品串在一起,1’指向2’，2’指向3’等等。

两个单链表相交的一系列问题

前置题目：如何判断一个单链表有无环，如果有环，返回第一个节点。

前置知识：如果一个单链表有环，那么环的第一个节点之后的节点都将在环内，不可能在环内分叉出去，那样就不符合单链表一个next指针的设定了。

笔试:

利用一个hashset，和一个指针，让指针从头结点开始走，走过这个节点后，就把这个节点放到hashset中。前提是：每走到一个节点，在hashset中搜索有没有这个节点，如果有那就是有环，并且第一次对比成功的节点就是环的第一个节点。

面试：要求空间复杂度为O(1)

用快慢指针，让快慢指针同时从头结点开始，慢指针走一步，快指针走两步，当快慢指针相遇时，此时可能并不是在环的第一个指针相遇，但是快慢指针在相遇前、进入环后这个时间段内，快指针走的圈数不可能超过2圈，所以不用担心快慢指针无法相遇或者相遇花费时间太长。在相遇时，定义一个慢指针指向头结点，让这两个慢指针同时走，当两慢指针相遇的时候，他们必定处于环的第一个节点，（记住结论就行，数学方法可证明），这样就找到环第一个节点了。如果快指针走到null，那就说明没有环。

【题目】给定两个可能有环也可能无环的单链表，头节点head1和head2。请实现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交，返回null

【要求】如果两个链表长度之和为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

由前置题目可以算出来一条单链表是否有环，并且可以得出环的第一个节点。

情况一：两条链表都没有环，相交。如果两个单链表都没有环，那么他们从相交位置到结尾都是共用同一部分。先让两个指针分别从头开始走到结尾，并统计两个链表的长度。比较结尾节点是否相等，如果相等说明两个链表相交。然后用长链表的长度减去短链表的长度，然后让长链表指针先走差值步数，然后再让短链表从头指针走，长链表指针也走，走一步对比一步，当相等时就是第一个相交节点位置。

情况二：一条有环，一条没环，相交。这种情况不可能存在，因为如果两链表相交，要是有环都必须有环，没环就都没环。

情况三：都有环。这种有三种情况

判断（2）：只要确定两个链表的环的第一个节点相同就可以确定是第二种情况。

判断（1）和（3）：这两个情况的loop不相等。在圈内loop1转的时候如果遇到第二个链表的loop节点，就可以确定是（3），如果没遇到就是（1）。情况3返回哪一个loop都行。

基础05(二叉树)

二叉树节点结构

二叉树中为k的父节点，它的左子节点下标为2k+1，右子节点是2k+2。

二叉树中为i的子节点，它的父节点下标为(i-1)/2

class Node{ 
    V value; 
    Node left; 
    Node right; 
}

用递归和非递归两种方式实现二叉树的先序、中序、后序遍历

前置知识：递归序是指只遍历，先中后左后右，不打印。递归实现的先序中序后序遍历都是在第一次或者第二次或者第三次经过节点时打印，区别只是在打印顺序。

递归：

public static void preOrderRecur(Node head) {
		if (head == null) {
			return;
		}
		System.out.print(head.value + " ");
		preOrderRecur(head.left);
		preOrderRecur(head.right);
	}

	public static void inOrderRecur(Node head) {
		if (head == null) {
			return;
		}
		inOrderRecur(head.left);
		System.out.print(head.value + " ");
		inOrderRecur(head.right);
	}

	public static void posOrderRecur(Node head) {
		if (head == null) {
			return;
		}
		posOrderRecur(head.left);
		posOrderRecur(head.right);
		System.out.print(head.value + " ");
	}

非递归：

非递归采用手动压栈的方法

先序：（1）从栈中弹出一个节点（2）打印弹出的节点（3）先右后左把子节点压入栈。周而复始，先序遍历完成。

中序：（1）每颗子树，整棵树左边界进栈，（2）依次弹出的过程中，打印，（3）对弹出节点的右树进行上述周而复始的操作。

中序遍历代码:

public static void preOrderUnRecur(Node head) {
		System.out.print("pre-order: ");
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			stack.add(head);
			while (!stack.isEmpty()) {
				head = stack.pop();
				System.out.print(head.value + " ");
				if (head.right != null) {
					stack.push(head.right);
				}
				if (head.left != null) {
					stack.push(head.left);
				}
			}
		}
		System.out.println();
	}

后序：申请两个栈，一个用来压栈，一个用来收集弹出的节点

（1）弹出cur节点 （2）cur节点放入收集栈 （3）先左后右把孩子压入压栈。周而复始，最后依次弹出收集栈里的数字，就是后序遍历结果。先序和后序的区别在于放子节点的顺序，一个先右后左，一个先左后右。

如何直观的打印一颗二叉树

老师提供了一个printTree函数，可以打印二叉树，方便我们观察自己造出来的二叉树。这个二叉树顺时针旋转90度就是真实的二叉树。第一张图是打印的，前后两个H表示根节点，前后两个v表示父节点在自己的左方偏下，前后两个^表示父节点在自己的左方偏上。最后把画出来的图顺时针旋转90°就行了。

public static void printTree(Node head) {
		System.out.println("Binary Tree:");
		printInOrder(head, 0, "H", 17);
		System.out.println();
	}

	public static void printInOrder(Node head, int height, String to, int len) {
		if (head == null) {
			return;
		}
		printInOrder(head.right, height + 1, "v", len);
		String val = to + head.value + to;
		int lenM = val.length();
		int lenL = (len - lenM) / 2;
		int lenR = len - lenM - lenL;
		val = getSpace(lenL) + val + getSpace(lenR);
		System.out.println(getSpace(height * len) + val);
		printInOrder(head.left, height + 1, "^", len);
	}

	public static String getSpace(int num) {
		String space = " ";
		StringBuffer buf = new StringBuffer("");
		for (int i = 0; i < num; i++) {
			buf.append(space);
		}
		return buf.toString();
	}

如何完成二叉树的宽度优先遍历（层序遍历）

对于二叉树来说。他的先序遍历就是深度优先遍历

宽度优先需要用到队列。先把头结点放进队列，然后头结点弹出，然后先左后右把孩子放进队列，然后再弹出再放入，周而复始直至队列为空。

ps：在java中LinkedList就是队列，其本身是个双向链表。

Queue<Node> queue = new LinkedList<>();  

求一棵二叉树的宽度

（不是高度）

方式一：申请一个队列和一个hashmap，定义三个变量，分别代表当前层级，当前层级有多少个节点，所有层级的最大个数。队列用来控制遍历操作，hashmap用来记录每个节点的层级。

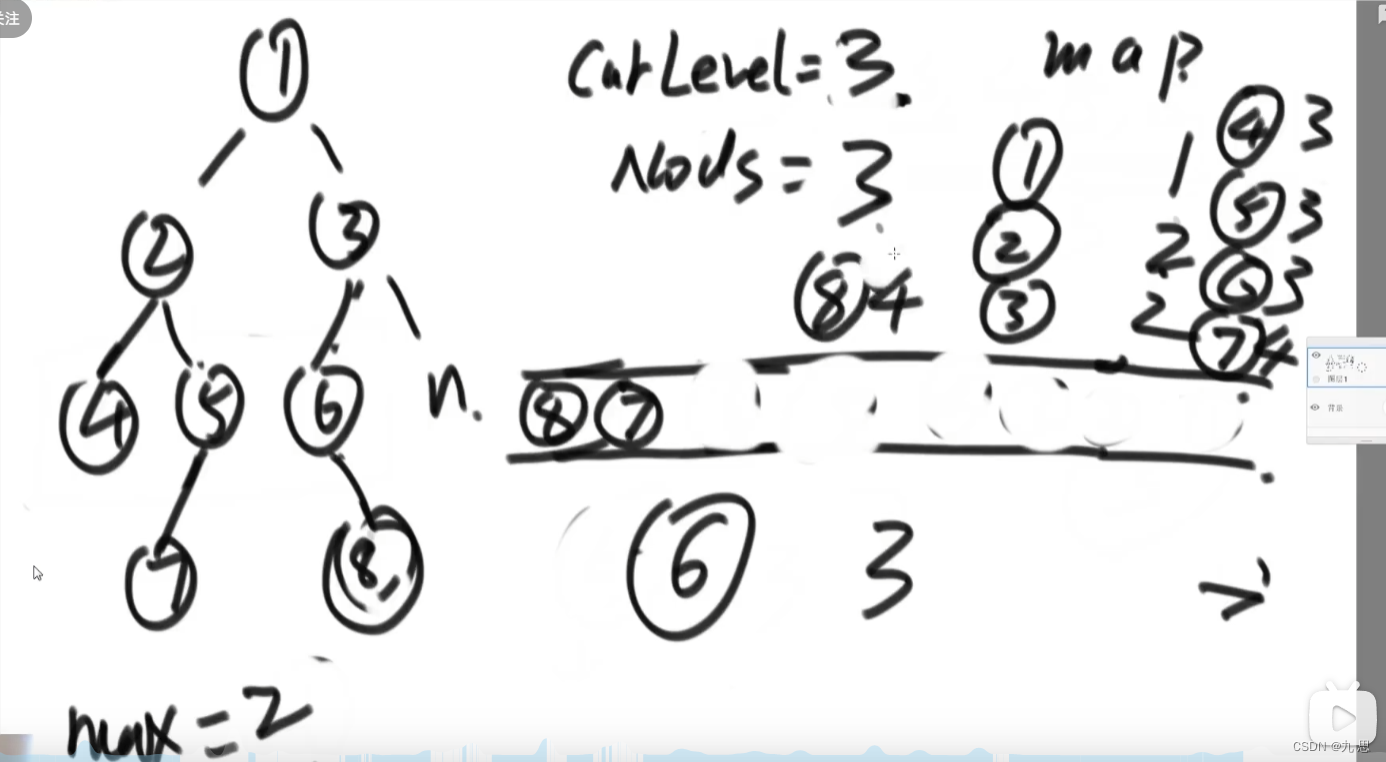
先把头结点放入队列，设置当前层级为1，然后出队，当前层级节点数+1，然后放入左右孩子，此时把左右孩子对应的层级放入hashmap，因为孩子的层级永远比父母高一级，所以孩子的层级很容易算出来，放入hashmap后，查看队列头结点的层级是多少，如果层级数和当前层级不一致，说明到达的新的层级，然后把上一层的总个数结算一下，设置一下max。并且设置当前层级+1，当前层级节点个数为1，下一个节点如果还是该层级，就把层级节点个数++，如此循环，当队列里没有节点的时候，结算一下当前层级的个数。最终得出来最大的层级个数。

public static int getMaxWidth(Node head) {
		if (head == null) {
			return 0;
		}
		int maxWidth = 0;
		int curWidth = 0;
		int curLevel = 0;
		HashMap<Node, Integer> levelMap = new HashMap<>();
		levelMap.put(head, 1);
		LinkedList<Node> queue = new LinkedList<>();
		queue.add(head);
		Node node = null;
		Node left = null;
		Node right = null;
		while (!queue.isEmpty()) {
			node = queue.poll();
			left = node.left;
			right = node.right;
			if (left != null) {
				levelMap.put(left, levelMap.get(node) + 1);
				queue.add(left);
			}
			if (right != null) {
				levelMap.put(right, levelMap.get(node) + 1);
				queue.add(right);
			}
			if (levelMap.get(node) > curLevel) {
				curWidth = 0;
				curLevel = levelMap.get(node);
			} else {
				curWidth++;
			}
			maxWidth = Math.max(maxWidth, curWidth);
		}
		return maxWidth;
	}

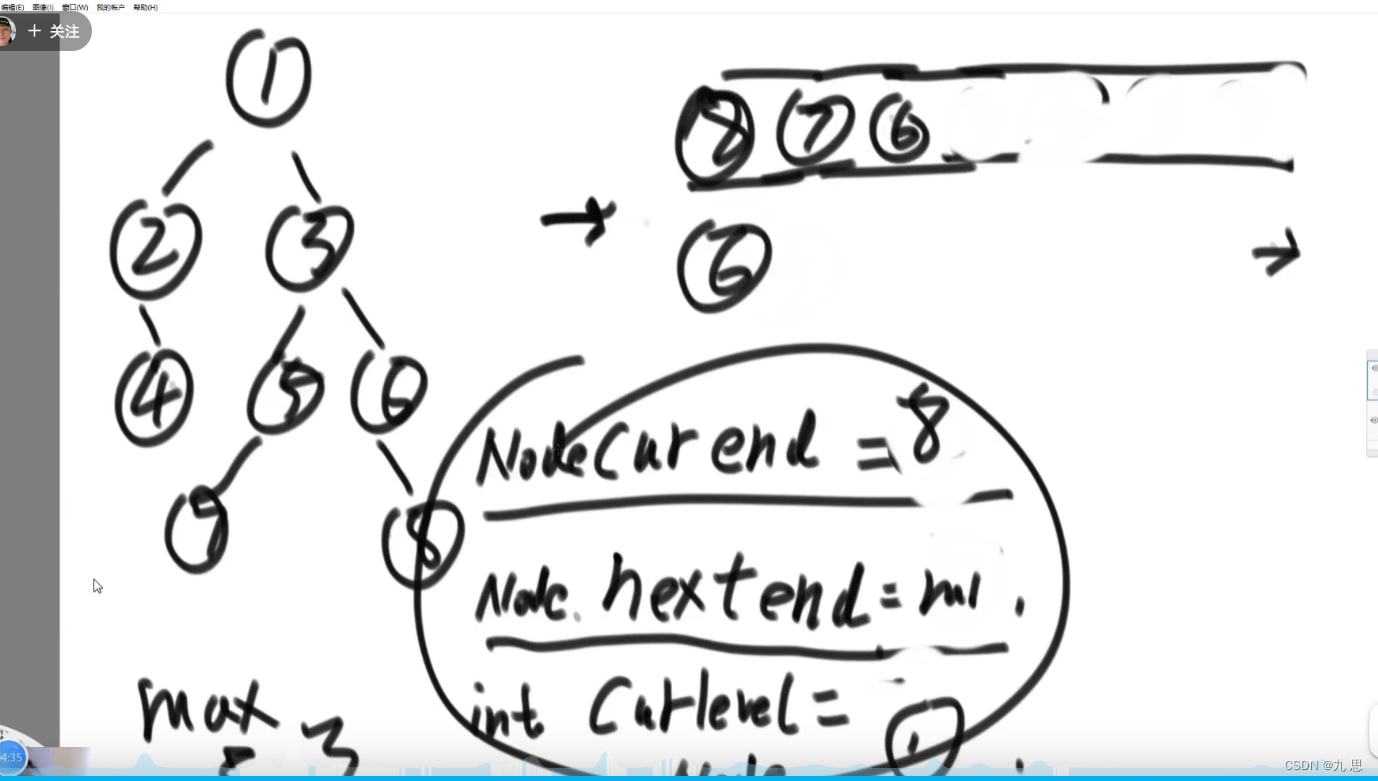
方式二：不用hashmap，声明一个Node类型的curEnd代表当前层级的最后一个数，声明一个Node类型的nextEnd代表下一层级的最后一个数。声明curLevelNodes代表当前层级的节点个数。max代表最大值。先初始化curEnd为1，然后弹出1，curLevelNodes++，判断弹出的1是不是curEnd，如果是那就更新max。弹出后需要把2,3入队，并且设置nextEnd为3。更新max后需要设置curENd为nextEnd，nextEnd设置为null，curLevelNodes设置为0。然后判断2有没有孩子，有孩子则在出队前把孩子入队，入队后更新nextEnd。2出队时判断自己是不是curEnd，不是。然后出队3后入队5,6。3出队，判断3位curEnd，然后像处理1一样处理3–更新curend，nextend，curlevelnodes，max。循环知道队列为空。为空之后再更新一次max。

二叉树的相关概念及其实现判断

如何判断一颗二叉树是否是搜索二叉树？

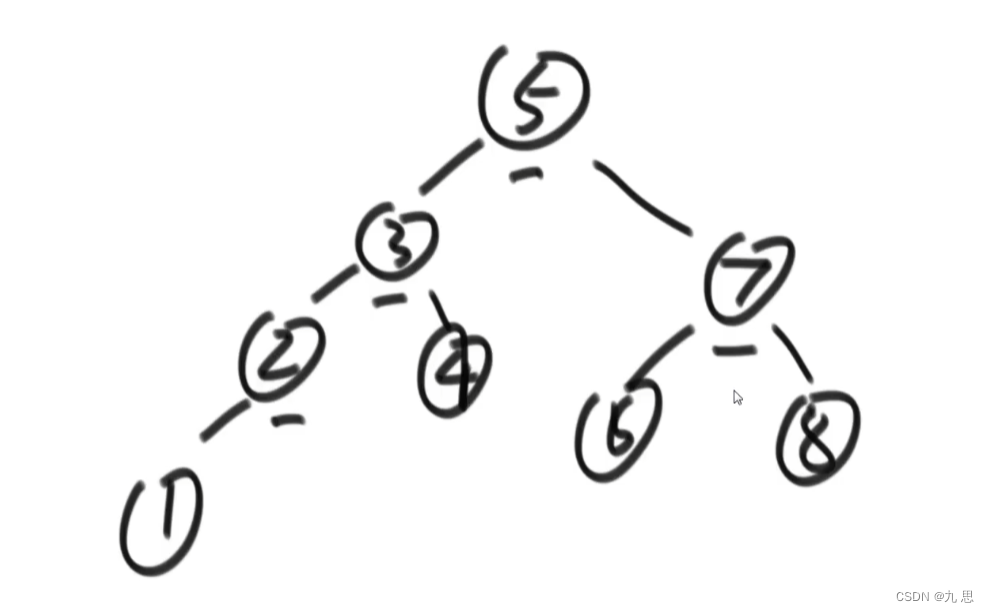
搜索二叉树的所有节点的左子树上的值一定比它小，右子树上的节点一定比它大。一个经典的二叉树里是不能有重复值。

中序遍历二叉树，如果结果是升序那么就是搜索二叉树。

方法一：声明一个preValue，代表已经比较的前一个值。然后在中序遍历的基础上，把打印的步骤修改为对比的步骤，每次对比的目前值都要比preValue大，对比完需要修改preValue为当前值。如果对比解释，都是当前值大于preValue值，说明是二叉搜索树。

方法二：中序遍历，把所有值依次放进一个数组里，然后判断数组是否升序，如果是升序，说明是二叉搜索树。

如何判断一颗二叉树是完全二叉树？

(1)完全二叉树不能只有右孩子而没有左孩子

(2)如果遇到了第一个只有左孩子没有有孩子的节点，那么后续的节点都必须为叶子结点。

解题方法：层序遍历。coding保证这两个条件。具体代码参考Code05_isCBT.java

如何判断一颗二叉树是否是满二叉树？

利用下面的套路，进行树形DP。向左右子树要信息，分别是高度和个数。然后再把自身的高度和个数算进去，得出整体的高度l和个数N。最后得出判断是否满足 N=2的l次方-1 。如果满足就是满二叉树。

public static boolean isF(Node head){
	if(head == null){
		return true;
	}
	Info data = f(head);//递归方法
	return data.nodes = 1 << data.height - 1;//1左移data.height位
}

public static class Info{
    public int height;
    public int nodes;
    public Info(int h,int n){
        height h;
        nodes n;
    }
}
public static Info f(Node x){
	if(x == null){
		return new Info(0,0);
    }
	Info leftData = f(x.left);
	Info rightData = f(x.right);
	int height = Math.max(leftData.height,rightData.height)+1;
	int nodes = leftData.nodes + rightData.nodes + 1;
	return new Info(height,nodes);
}

如何判断一颗二叉树是否是平衡二叉树？

什么是平衡二叉树？对于任何一个子树，他的左子树和右子树的高度差不超过1

需要保证三个条件才能确定是平衡二叉树：

1. 左子树是平衡数
2. 右子树是平衡树
3. 左子树和右子树的高度差不超过1

我们现在需要左子树提供一些信息：左子树是否是平衡树？左子树的高度？右子树也一样。知道这些信息再判断整个数是否是平衡二叉树。自然而然判断出来这题要使用递归。

注意：当前树的高度是左子树和右子树两个树中最高的树高度+1。

二叉树题目套路 ☆☆☆

树形DP

由上一题可以看出一个规律，在二叉树这类题中，我们可以向左子树要一个信息，右子树要一个信息，判断左右子树的信息是否符合我们的需求。比如判断是否是搜索二叉树这道题，我们向左子树要两个信息：左子树是不是搜索树、左子树的节点最大值；向右子树要两个信息：右子树是不是搜索树、右子树节点的最小值。然后判断左右子树是不是搜索树，当前节点是不是大于左子树的最大值，并且小于右子树的最小值，如果都满足，那说明当前子树是搜索树。这种套路是树形DP。在面试时面试官很可能会根据是否会这个套路做题来区分面试者。

二叉树题目

二叉树一般可以用递归解

给定两个二叉树的节点node1和node2，找到他们的最低公共祖先节点

第一种比较好理解的方法：从根节点开始依次遍历，把所以节点和他的father存到hashmap中，然后从node1开始，把自己和他的父亲，存到hashset中，并且把他父亲的父亲。。。。，直到根结点，形成一个链路。然后从node2开始向他的父亲方向移动，然后比较父亲节点在不在hashset中，如果存在那说明当前父亲节点就是他们最低公共祖先，如果不是，继续向上移动，直到根结点，如果还没遇到，那最低公共祖先就是根结点了。如果到了根节点，左右子树返回值中，只有一个节点返回那么该返回的节点就是他们的公共祖先节点，即两个node中的某一个。

第二种比较优秀的方法：采用递归的方式，判断左右子树中是否存在两个node节点中的一个，如果没有返回null，如果有就返回该node。当发现两个子树都分别存在一个node，那么该节点就是最低公共祖先节点。具体代码参考Code07_LowestCommonAncestor.java

在二叉树中找到一个节点的后继节点

【题目】 现在有一种新的二叉树节点类型如下:

public class Node { 
    public int value; 
    public Node left; 
    public Node right; 
    public Node parent; 
    public Node(int val) { 
        value = val; 
    } 
} 

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。

假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。

只给一个在二叉树中的某个节点node，请实现返回node的后继节点的函数。

在二叉树的中序遍历的序列中，node的下一个节点叫作node的后继节点

解题：

（1）某节点如果有右节点，那么该节点的后继节点是其右子树的最左节点（从右子树的根一直往左，左到头就行）。

（2）如果x无右树，那么看一下x是不是其父亲的左孩子，如果不是左孩子，继续向父辈看，当某个节点是左孩子时，那么左孩子的父亲是x的后继节点。因为x是左子树最右的节点，只要打完x，就打印y。具体代码参考：Code08_SuccessorNode.java

二叉树的序列化和反序列化

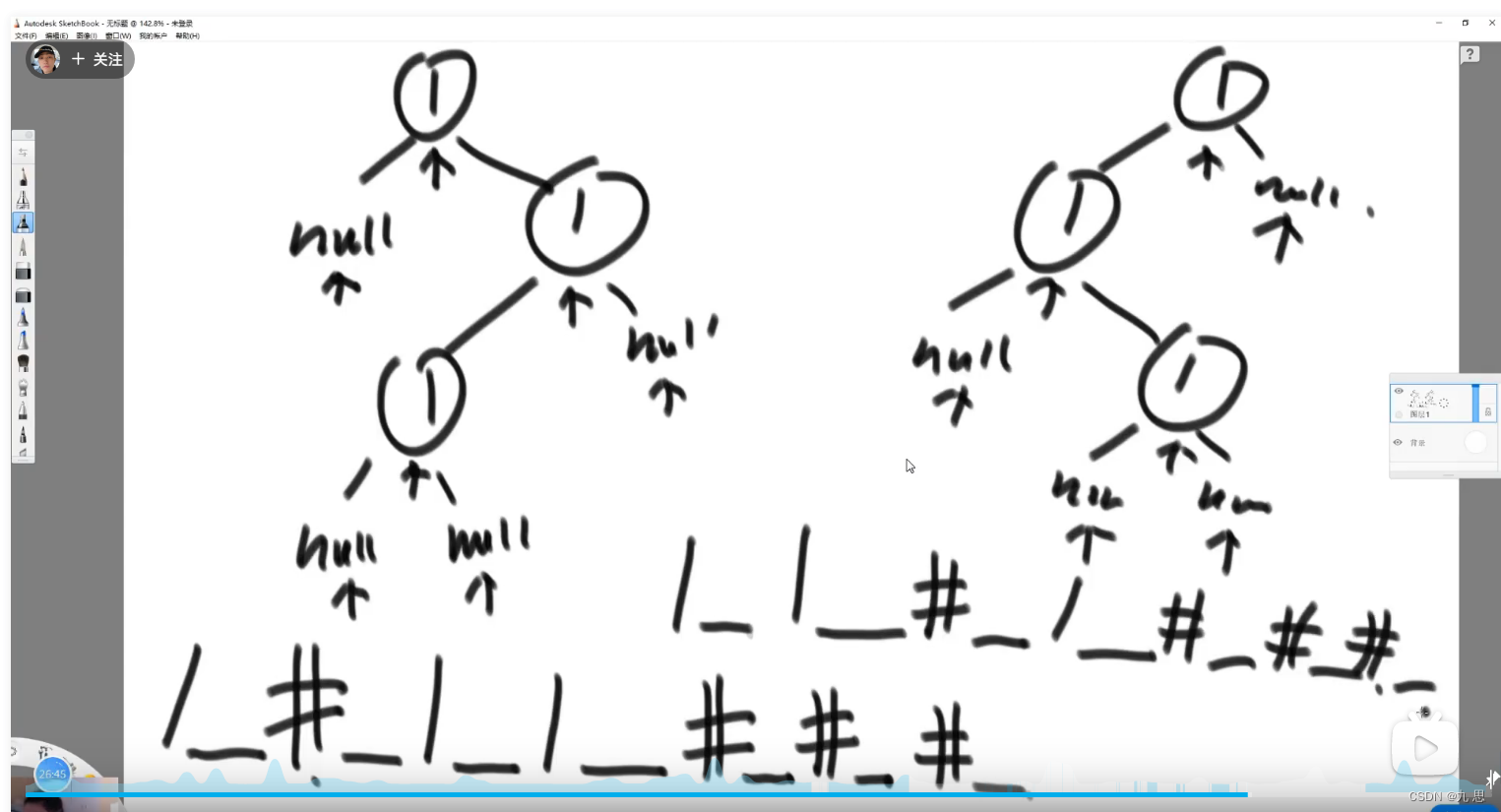
就是内存里的一棵树如何变成字符串形式，又如何从字符串形式变成内存里的树

按先序中序后序都行，遍历这棵树，这里选择先序遍历，把遍历到的节点依次写入数组，如果子树为null，需要特殊表示出来。比如下图用1表示节点值，#代表null，_表示分割意思。把二叉树变成了一个字符串，这相当于序列化。然后把字符串按照“__”分割，遍历数组，把数组按照先序遍历依次还原，这是反序列化。具体参考Code09_SerializeAndReconstructTree.java

折纸问题

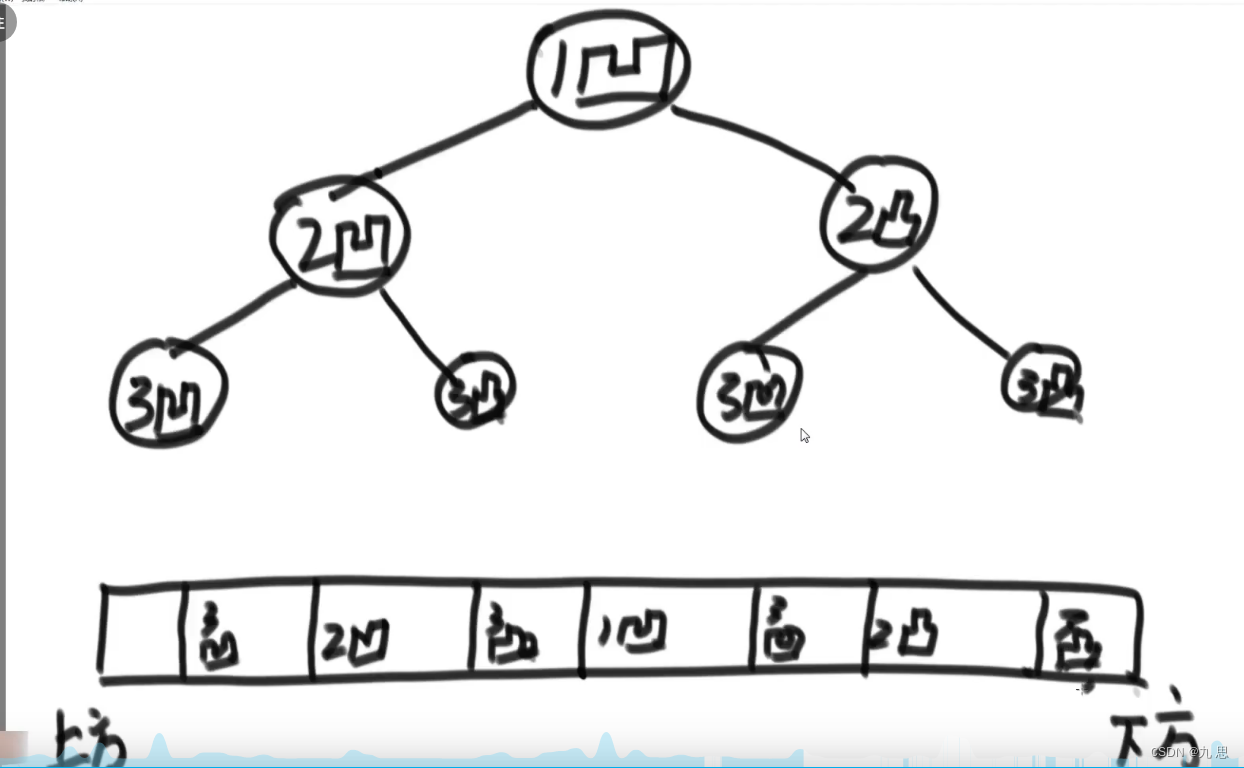
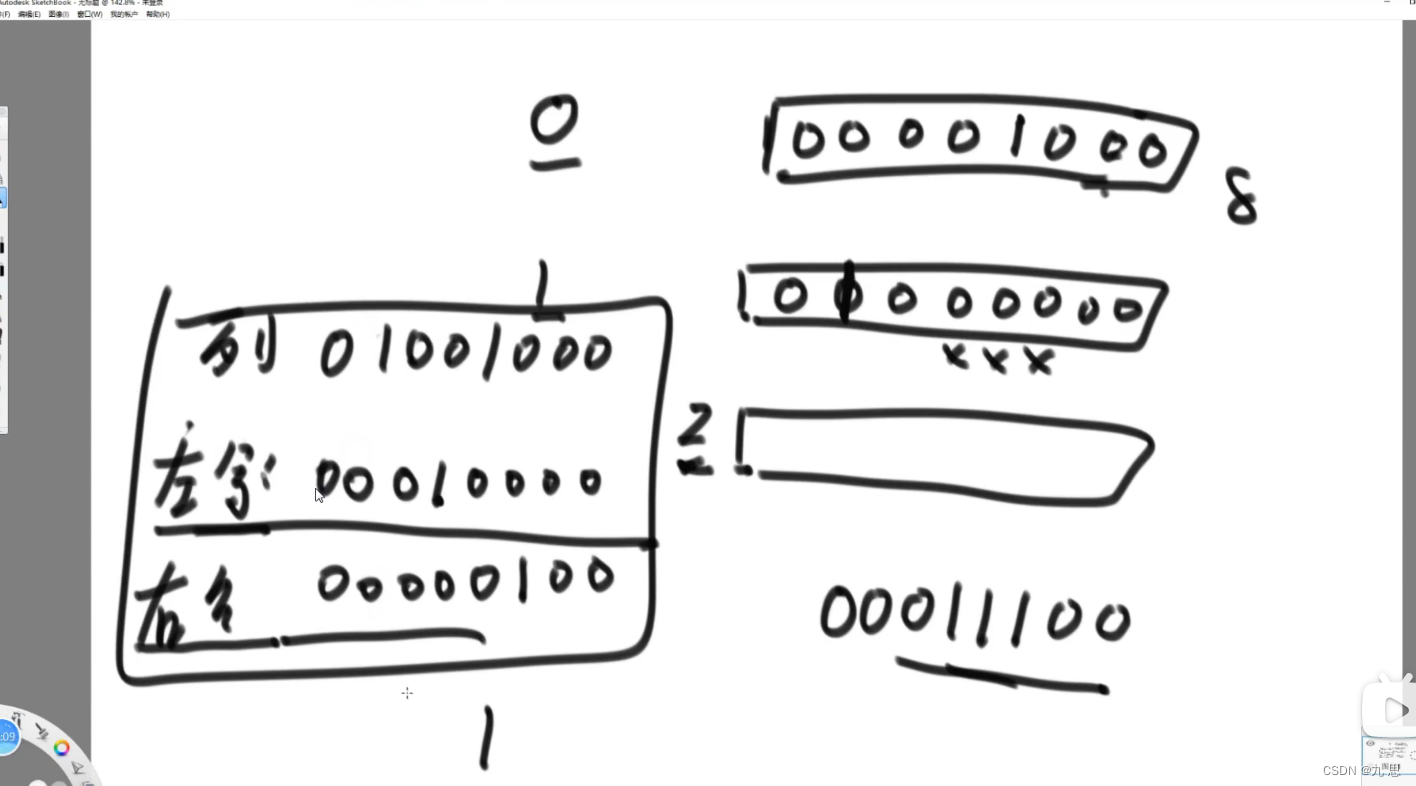
请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。 此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。 如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从 上到下依次是下折痕、下折痕和上折痕。

给定一个输入参数N，代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。 例如:N=1时，打印: down N=2时，打印: down down up

第一次对折，会产生1凹折痕。第二次对折，会在1凹的上边产生2凹，下边产生2凸。第三次对折，会在2凹的上边产生3凹，下边产生3凸；在2凸的上边产生3凹，下边产生3凸。这可以类比成二叉树。这里也不用生成二叉树，然后再中序遍历二叉树。而是在脑子里模仿生成一个二叉树，在第二次到达节点时打印就行。每次在父节点产生孩子节点都是左凹右凸。代码参考Code10_PaperFolding.java

基础06(图)

图的存储方式

1)邻接表

2)邻接矩阵

3）其他

可以用邻接表或邻接矩阵来表示图。也可以用其他特殊的数据结构表示图，比如一个一维数组，数组的下标代表起始点，下标对应的值代表目的地，这样来表示。图的题难就难在表达图的方式有很多种，不同的表达方式实现算法的具体形势也不同，要根据不同的数据结构变换。不过公司面试一般不太可以让我们用不同的数据结构表示图，基本上能用数组表示就行，不做过多要求。在遇到自己不太熟悉的数据结构时，左神推荐写一个接口，把自己熟悉的数据结构里的内容转化为题目要求的数据结构，其他部分基本就可以保持不变了，从而不容易出错。

图的算法不难，难就难在处理不同的表示图的数据结构这一步骤

邻接表：用每一行的表头代表出发点，后边跟上各个目的地，如果有距离，还可以在目的地上加上距离。

邻接矩阵：一个正方形矩阵，可以用行表示出发点，列表示目的地，(行，列)位置上的值表示距离

左神用的表示图的数据结构：

public class Graph {
	public HashMap<Integer,Node> nodes; //<点的编号，实际节点>
	public HashSet<Edge> edges;//图的边集

	public Graph() {
		nodes = new HashMap<>();
		edges = new HashSet<>();
	}
}

public class Node {
	public int value;//节点值
	public int in;//入度
	public int out;//出度。  无向图的入度和出度相等
	public ArrayList<Node> nexts;//从A发散出去边指向的直接节点，A指向B、C，那么nexts就包含B、C
	public ArrayList<Edge> edges;//A发散的边，不包含指向A的边

	public Node(int value) {
		this.value = value;
		in = 0;
		out = 0;
		nexts = new ArrayList<>();
		edges = new ArrayList<>();
	}
}

public class Edge {
	public int weight;//常用来表示距离
	public Node from;//起始点
	public Node to;//结束点

	public Edge(int weight, Node from, Node to) {
		this.weight = weight;
		this.from = from;
		this.to = to;
	}

}

/*创建图*/
public class GraphGenerator {

	public static Graph createGraph(Integer[][] matrix) {//matrix是用户给的数组，每一行第一个是权重，第二个是起点，第三个是终点；根据数组转化出来图
		Graph graph = new Graph();
		for (int i = 0; i < matrix.length; i++) {
			Integer weight = matrix[i][0];
			Integer from = matrix[i][1];
			Integer to = matrix[i][2];
			if (!graph.nodes.containsKey(from)) {
				graph.nodes.put(from, new Node(from));
			}
			if (!graph.nodes.containsKey(to)) {
				graph.nodes.put(to, new Node(to));
			}
			Node fromNode = graph.nodes.get(from);
			Node toNode = graph.nodes.get(to);
			Edge newEdge = new Edge(weight, fromNode, toNode);
			fromNode.nexts.add(toNode);
			fromNode.out++;
			toNode.in++;
			fromNode.edges.add(newEdge);
			graph.edges.add(newEdge);
		}
		return graph;
	}

}

图的宽度优先遍历

1，利用队列实现

2，从源节点开始依次按照宽度进队列，然后弹出

3，每弹出一个点，把该节点所有没有进过队列的邻接点放入队列

4，直到队列变空

采用了一个队列和一个set，队列控制遍历顺序，set表示已经遍历的节点。先把第一个节点入队，并且把这个节点放入set，记录set已经遍历过，然后set弹出，然后把set的nexts节点入队，然后循环，直到队列为空，遍历结束。

注意：当节点数较少的时候（比如城市数），可以用数组代替set，因为虽然set是O(1)，但是也比数组寻址慢。

public static void bfs(Node node) {
	if (node == null) {
		return;
	}
	Queue<Node> queue = new LinkedList<>();
	HashSet<Node> map = new HashSet<>();
	queue.add(node);
	map.add(node);
	while (!queue.isEmpty()) {
		Node cur = queue.poll();
		System.out.println(cur.value);
		for (Node next : cur.nexts) {
			if (!map.contains(next)) {
				map.add(next);
				queue.add(next);
			}
		}
	}
}

深度优先遍历

1，利用栈实现

2，从源节点开始把节点按照深度放入栈，然后弹出

3，每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈

4，直到栈变空

整体思想是找到一条路就走到黑，之后退回去，每退一步，就判断栈顶元素有没有未遍历的nexts节点，如果没有就弹出这个节点，如果有就在nexts中选一个入栈，循环直到栈为空。

从一个节点，把这个节点压入栈，在出栈的时候，在他的nexts节点中挑选一个，然后把这个节点和next节点压入栈，（每个节点在压入栈时都要添加到set里，表明已经遍历过），然后把next节点出栈，再看next节点的next节点有哪些，从中选一个，把next节点和他的next节点入栈，循环直到栈为空。

拓扑排序

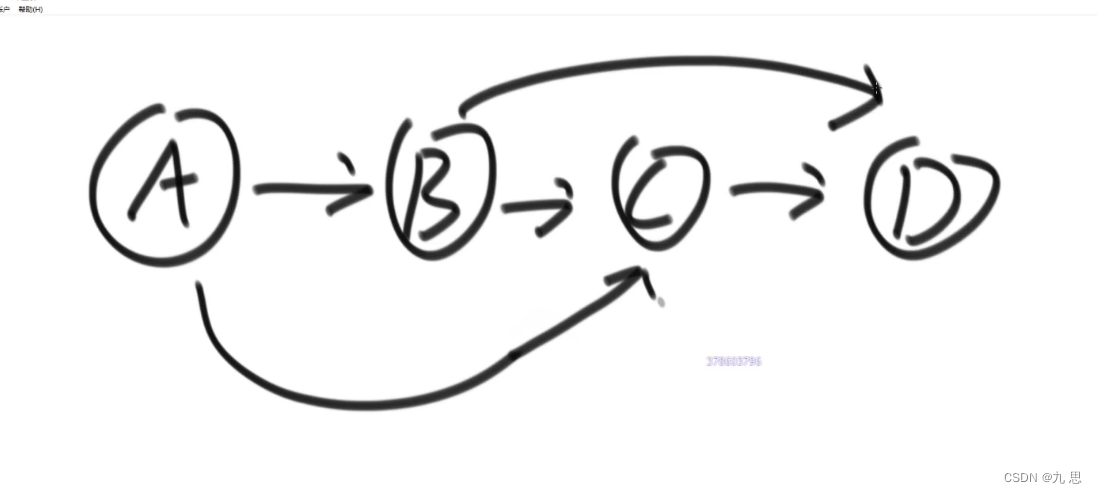
适用范围：要求有向图，且有入度为0的节点，且没有环

实例：写项目需要用到maven控制依赖，比如我这个项目是A，我要依赖B、C才能编译起来，那我就需要先编译B、C，而B又需要依赖D，需要D先编译。在拓扑排序里，这个例子的排序就是ABCD

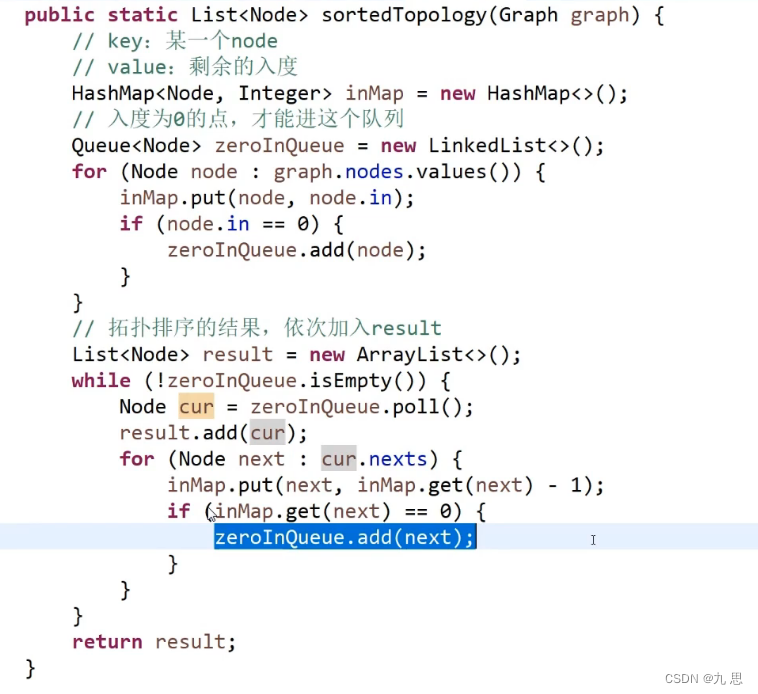
算法思路：需要用到一个map和一个queue。先遍历图的节点，把每个节点及其入度存到map里，在遍历到每个节点的时候，判断他的入度是不是0，如果是0，就把他放进队列里。每次循环，找到图中的入度为0的节点，然后把这些节点入队，然后在节点出队的时候，把他指向其他节点的影响去掉，也就是修改map，把指向的节点的入度-1，最后把从队列出队的节点放进结果数组。队列为空时，拓扑排序完成。

代码：

kruskal算法

适用范围：要求无向图。

目的：用来生成最小生成树。

前置知识：最小生成树

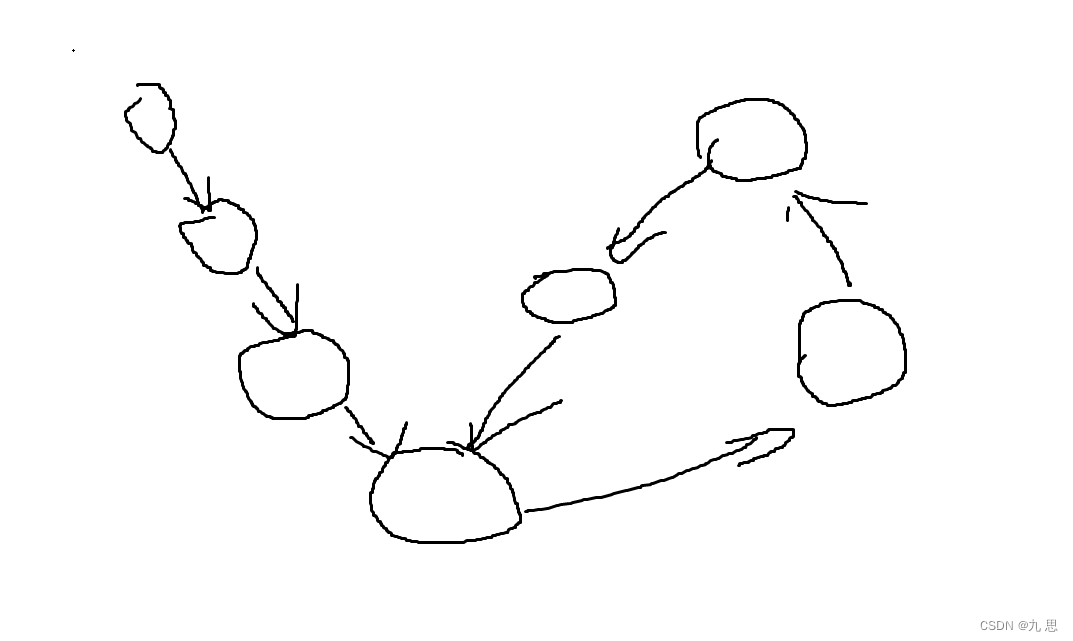
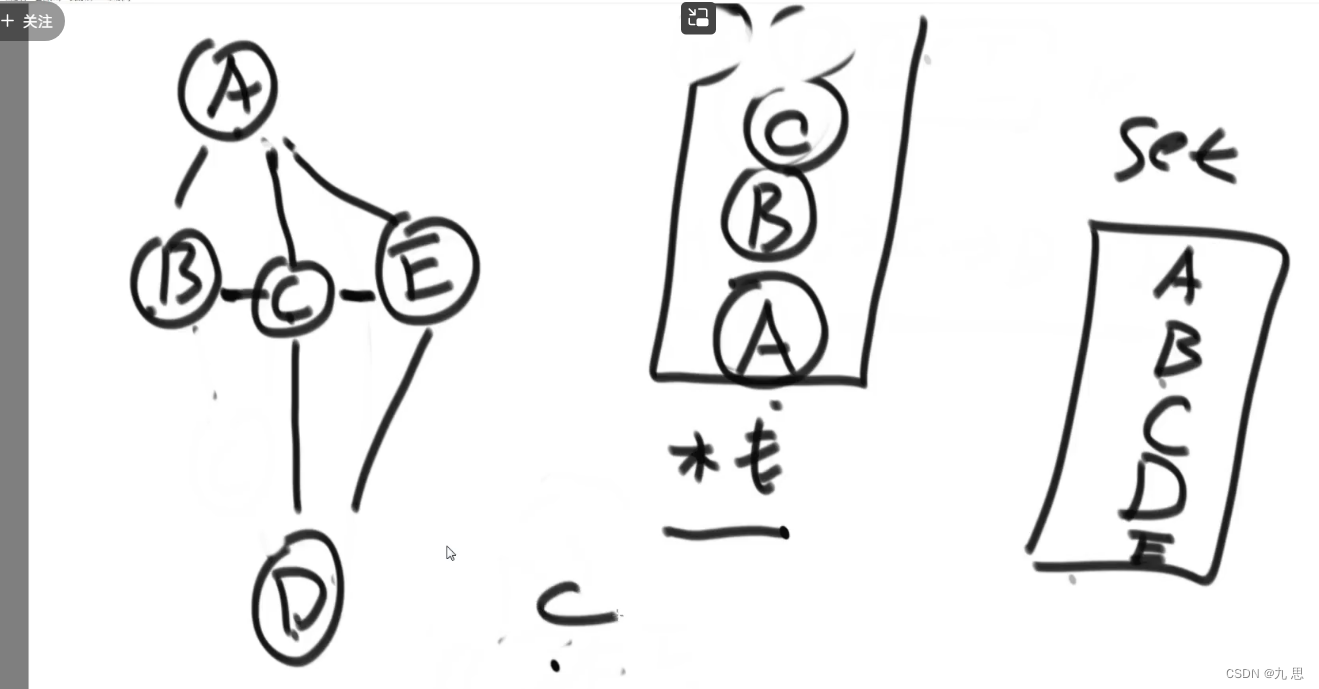
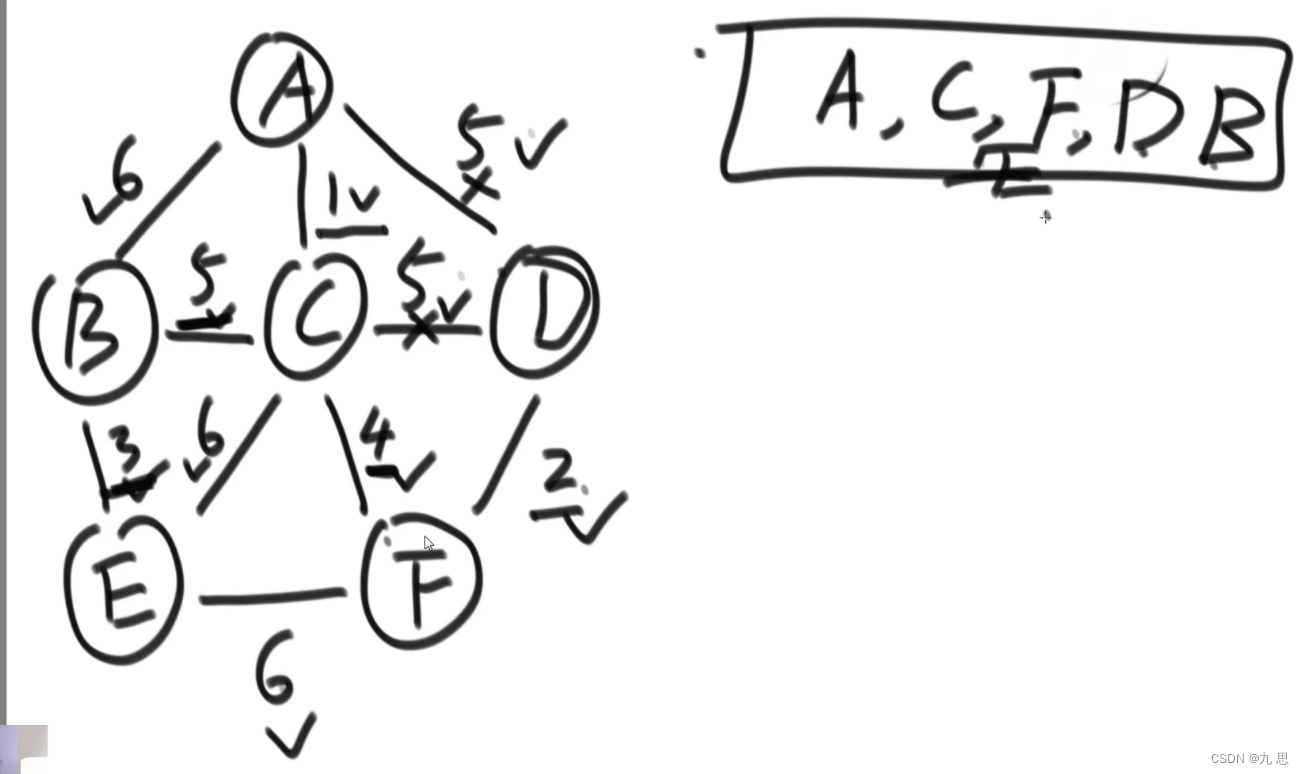
在下图中，左边的图是原图，右边是他的最小生成树。最小生成树是指能保证图的所有节点是连通的同时所有边的权重和最小。（间接连通也符合要求，因为是无向图）

算法思路：k算法是从边的角度出发的。先把所有边按照权重排一个序，然后每次按照当前未添加到图中的边中选最小边，尝试插入到图中，如果插入后没有出现环，那么说明这个边可以插入，然后判断下一个最小边可不可以插入。当所有边判断完，生成了最小生成树。那么如何判断当前图有没有环呢？

算法实现：先把图的所有节点放进并查集，每一个节点对应有它所在的集合。然后声明一个小根堆（需要传入排序方式），把所有边放入小根堆。每弹出一个边，用并查集判断边的from和to在不在一个集合，如果不在，那么把边放入结果集，并且合并两个集合；如果在，那就不考虑这条边。循环，直到小根堆为空。结果集创造完成。

判断是否有环：先把每个节点都放到它单独一个集合里，A独自一个集合、B独自一个集合、C独自…… 然后判断第一最短边的from和to两个节点，如果他们两个没有在同一个集合，那么这条边就可以插入，然后判断下一条边的from和to在不在同一集合，如此循环直到所有边遍历完成。

这个算法的实现需要并查集，但是并查集是在基础提升里讲，老师给了一个简单的数据结构来实现功能，可能不想并查集那么快，但是实现起来比较简单。

MySets结构存储了图中节点和它对应的集合：

剩余代码参考 Code04_Kruskal.java

prim算法

适用范围：要求无向图。

目的：用来生成最小生成树。

本算法是从节点出发考虑的。

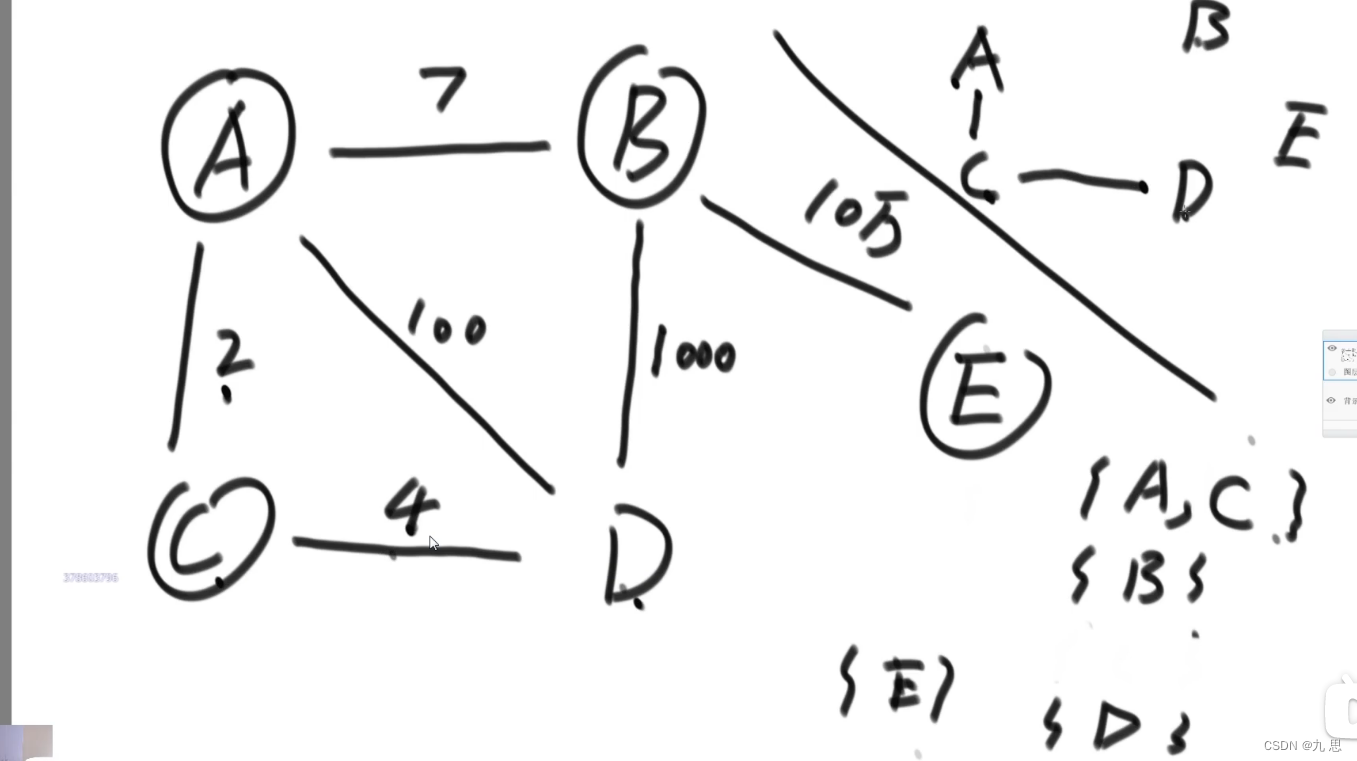
算法思路：本算法使用了一个set来保存已经形成通路的节点，一个小根堆来存放解锁的边。如下图，开始时，随机选择一个节点开始，把这个节点相关的边全部放入小根堆中，然后把根节点弹出，得到一条边，然后判断边的to节点是否存在set中，如果不存在，就把to节点放入set，表示已经形成通路，并且把这条边放到结果集里；如果存在，就跳过这条边，继续判断小根堆的根节点，循环到小根堆为空。重复添加相同边不会导致算法出错，因为后来重复加入的边，会被判断to在不在set里，肯定会被过滤掉，最多导致整体时间慢一点，但对结果无影响。

代码：

	public static Set<Edge> primMST(Graph graph) {
		PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(
				new EdgeComparator());//小根堆
		HashSet<Node> set = new HashSet<>();//记录已经通路的节点
		Set<Edge> result = new HashSet<>();//结果集
		for (Node node : graph.nodes.values()) {
		//用来处理存在森林的情况，如果不存在森林，那么第一次循环就可以解决所有节点的连通。但是如果存在森林，需要通过循环来确保每一个节点都经过处理。

			if (!set.contains(node)) { //如果没有形成通路，就可以解锁这个节点的相关边
				set.add(node);
				for (Edge edge : node.edges) {
					priorityQueue.add(edge);
				}
				while (!priorityQueue.isEmpty()) {
					Edge edge = priorityQueue.poll();
					Node toNode = edge.to;
					if (!set.contains(toNode)) {
						set.add(toNode);
						result.add(edge);
						for (Edge nextEdge : toNode.edges) {
							priorityQueue.add(nextEdge);
						}
					}
				}
			}
		}
		return result;
	}

Dijkstra算法

适用范围：不能有权值为负的边，或者说是不能有累加和权值为负的环。

目的：求最短路，即从某一个点开始，这个点到所有点距离都要是最小值

如果有负边，可能会导致前边算出来某个节点的最短路不是最短路了，导致算法出错。锁死是为了应对有负边的情况。

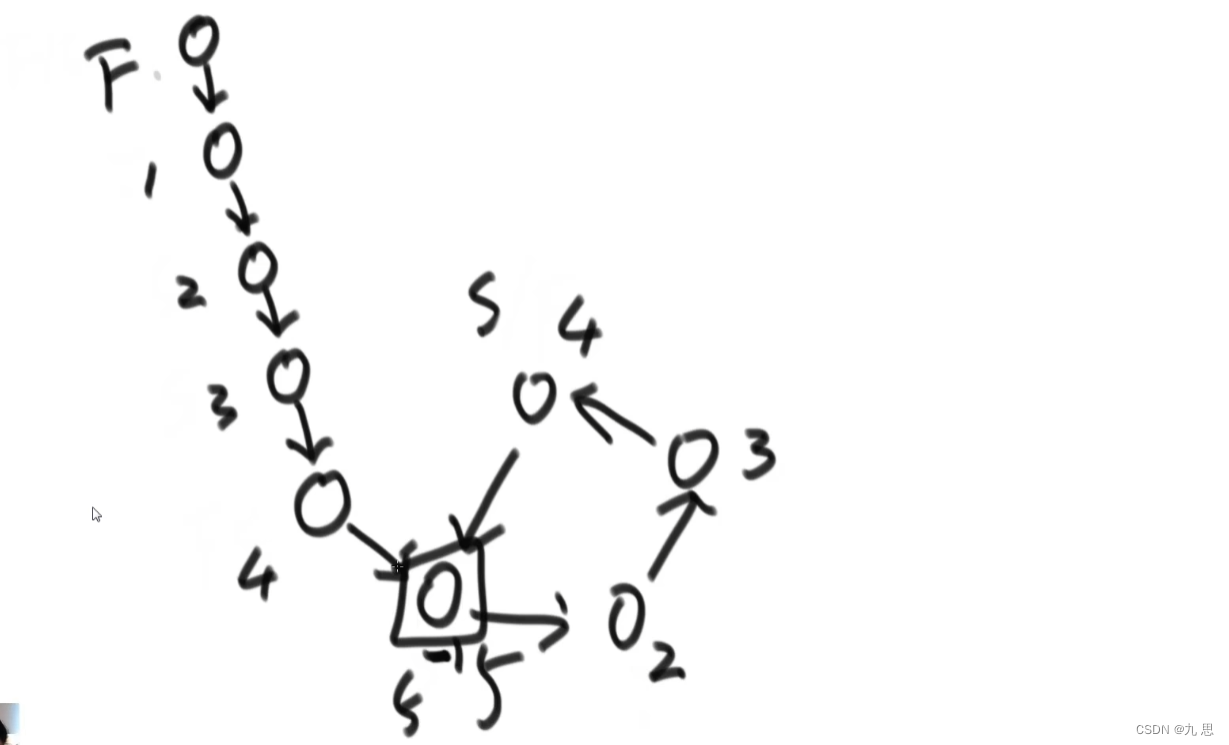
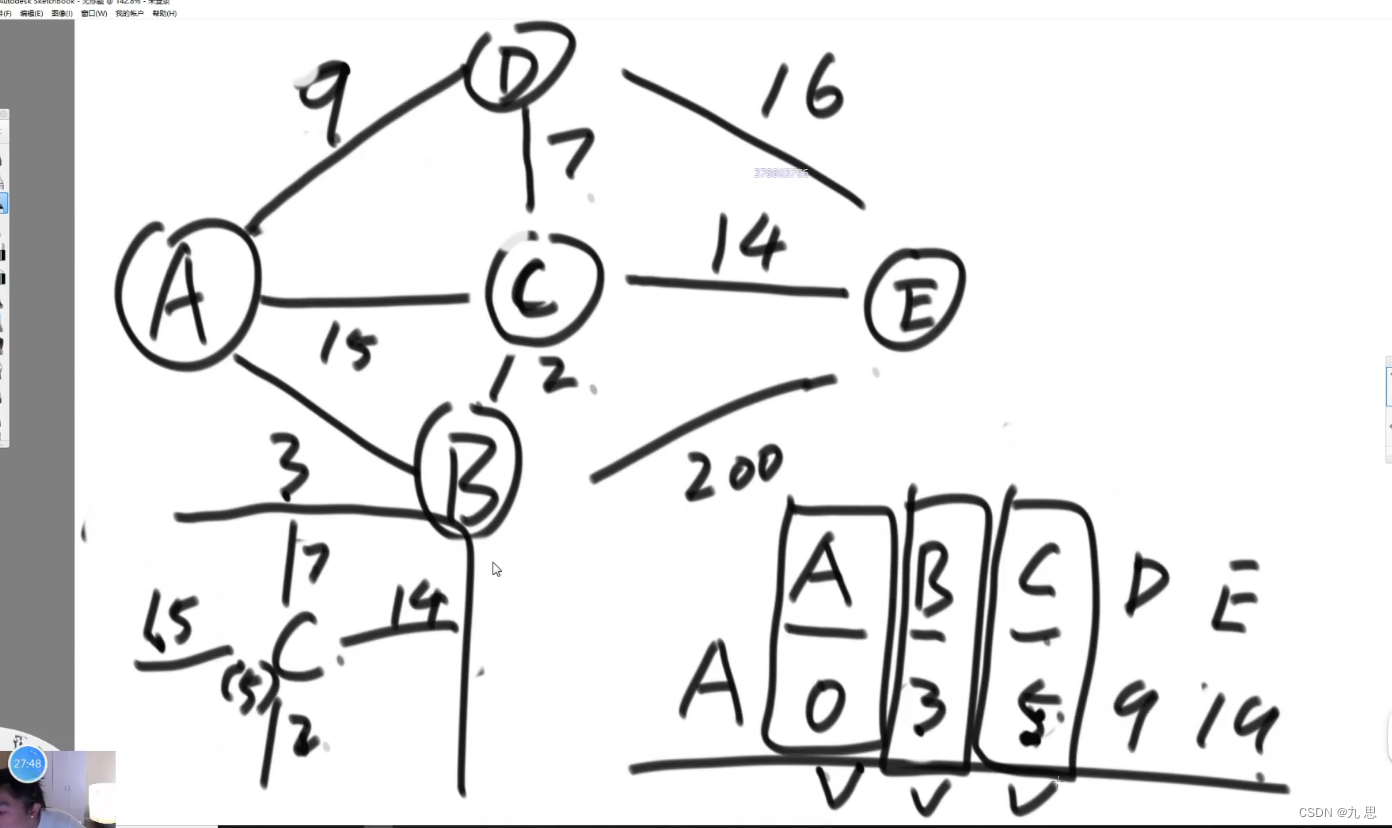
算法流程：先设置A到所有边的距离为正无穷。从起点A开始，找到和他相关的所有边，然后设置A到这些边的to节点的距离，然后找到这些边的最短边，然后走最短边到B，看B相关的边，B到C距离是2，能让A到C的距离从之前的变为A-B + B-C 等于5，然后看到E的边，从之前的无穷改为203。遍历完所有边后，设置到B的距离为不可改动。然后在B节点相关边找最短边，到C。C到E的距离是14，可以让A到E的距离变为19；然后从C到其他节点的距离都无法让A到这些节点的距离变更小。然后设置C为不可改动，再选出最短边C到D。看D的边，然后循环，直到A到所有节点的距离都锁定。

算法思路：主要是每个循环中，选出A到没有被锁定节点中的距离最小的节点，这个节点就是下一步要到的地方，然后到达这个地方，看一下这个地方的next路线能不能让之前A到这些路线的目的节点的距离变小，如果能变小就更新距离，如果不能就跳过。当所有可走的边都判断过之后，锁定当前节点，并选出下个节点，循环，直至所有节点被锁定。

代码：

public static HashMap<Node, Integer> dijkstra1(Node head) {
	//从head出发到所有点的最小距离
	//key:从head出发到达key
	//value:从head出发到达key的最小距离
	//如果在表中，没有T的记录，含义是从head出发到T这个点的距离为正无穷
	HashMap<Node, Integer> distanceMap = new HashMap<>();
	distanceMap.put(head, 0);
	//已经求过距离的节点，存在selectedNodes中，以后再也不碰
	HashSet<Node> selectedNodes = new HashSet<>();

	Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);//选出A到没有被锁定节点中的距离最小的节点
	while (minNode != null) {
		int distance = distanceMap.get(minNode);
		for (Edge edge : minNode.edges) {
			Node toNode = edge.to;
			if (!distanceMap.containsKey(toNode)) {
				distanceMap.put(toNode, distance + edge.weight);
			}
			distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
		}
		selectedNodes.add(minNode);
		minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
	}
	return distanceMap;
}

public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, 
		HashSet<Node> touchedNodes) {
	Node minNode = null;
	int minDistance = Integer.MAX_VALUE;
	for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
		Node node = entry.getKey();
		int distance = entry.getValue();
		if (!touchedNodes.contains(node) && distance < minDistance) {
			minNode = node;
			minDistance = distance;
		}
	}
	return minNode;
}

手写堆优化Dijkstra☆☆☆

用堆优化：在遍历查找下一步最短距离的节点的时候，我们可能会想到用系统提供的小根堆维护一个最小值。但是一旦堆中某个数在某个操作过程中变小了（改变了），那么系统提供的小根堆要重新维护出最小值这个过程是损耗很大的，几乎相当于全局扫描。系统提供我们的函数基本上只能用插入和弹出这两个，而其他的消耗太大。所以我们要手写堆。

代码：

public static class NodeRecord {//A到每个节点当前最短距离，用于封装
    public Node node;
    public int distance;

    public NodeRecord(Node node, int distance) {
        this.node = node;
        this.distance = distance;
    }
}

public static class NodeHeap {
    private Node[] nodes;//堆中节点
    private HashMap<Node, Integer> heapIndexMap;//数组的index，代表在模拟堆[数组]中的位置
    private HashMap<Node, Integer> distanceMap;//A到每个节点的当前距离
    private int size;

    public NodeHeap(int size) {
        nodes = new Node[size];
        heapIndexMap = new HashMap<>();
        distanceMap = new HashMap<>();
        this.size = 0;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public void addOrUpdateOrIgnore(Node node, int distance) {//如果是新来的那就添加；存在的就更新；
        if (inHeap(node)) {//如果本身在堆中，看这个距离是不是比distance大，大就更新；
            distanceMap.put(node, Math.min(distanceMap.get(node), distance));
            insertHeapify(node, heapIndexMap.get(node));//把对应位置的节点找到，然后从他开始堆化
        }
        if (!isEntered(node)) {//新来的，新建一个
            nodes[size] = node;
            heapIndexMap.put(node, size);
            distanceMap.put(node, distance);
            insertHeapify(node, size++);
        }
        //什么都不做代表ignore
    }

    public NodeRecord pop() {
        NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));//得到根的信息
        swap(0, size - 1);//这里传入的都是下标，最后一个就是size-1下标
        heapIndexMap.put(nodes[size - 1], -1);//修改根的下标为-1，代表曾经进入过堆，但是被弹出；之后再也不会把这个节点入队了，相当于把这个节点锁住，之后不考虑这个节点
        distanceMap.remove(nodes[size - 1]);
        nodes[size - 1] = null;
        heapify(0, --size);//让新根状态的小根堆,堆化
        return nodeRecord;
    }

    private void insertHeapify(Node node, int index) {
        //小于父节点的时候，和父节点交换位置；这里只用考虑变小的情况就行；因为流程里只会让最短距离逐渐变小而不会变大
        while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {
            swap(index, (index - 1) / 2);//交换位置需要对heapIndexMap，nodes进行调整
            index = (index - 1) / 2;//交换之后，子节点的下标等于之前父节点的距离，也就是之前的(i-1)/2
        }
    }

    private void heapify(int index, int size) {
        int left = index * 2 + 1;//左子节点
        while (left < size) {//左子树存在
            int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])
                ? left + 1 : left;//挑选左右子树最小的（如果右子树存在，不存在那就是左子树了）
            smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;
            //尝试对比，如果孩子比他小，那就把smallest原封不动；如果孩子比他大，那么修改smallest为index（父亲），说明已经满足小根堆，可以退出了
            if (smallest == index) {
                break;
            }
            //没有退出的情况下（孩子更小）
            swap(smallest, index);//交换两者位置
            //为下次循环准备条件
            index = smallest;
            left = index * 2 + 1;
        }
    }

    private boolean isEntered(Node node) {
        return heapIndexMap.containsKey(node);
    }

    private boolean inHeap(Node node) {
        return isEntered(node) && heapIndexMap.get(node) != -1;
    }

    private void swap(int index1, int index2) {
        heapIndexMap.put(nodes[index1], index2);
        heapIndexMap.put(nodes[index2], index1);
        Node tmp = nodes[index1];
        nodes[index1] = nodes[index2];
        nodes[index2] = tmp;
    }
}
public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
		NodeHeap nodeHeap = new NodeHeap(size);//初始化堆
		nodeHeap.addOrUpdateOrIgnore(head, 0);//先把头结点放入堆
		HashMap<Node, Integer> result = new HashMap<>();//存放A到每个节点的最短路径，存进去就相当于锁定了
		while (!nodeHeap.isEmpty()) {
			NodeRecord record = nodeHeap.pop();//弹出堆顶，找出未锁定的（即在堆中，且heapIndexMap中值不为-1（-1代表曾经进过堆但是被弹出去））最短节点
			Node cur = record.node;
			int distance = record.distance;
			for (Edge edge : cur.edges) { //遍历它的每条边，看to节点需不需要更新距离
				nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
			}
			result.put(cur, distance);
		}
		return result;
	}

基础07(前缀树、贪心)

前缀树

也叫字典树、Trie树

何为前缀树? 如何生成前缀树?

问题场景：给一个字符串数组，问这些数组里有没有出现过某个字符串？或者以“ab”为前缀的字符串有多少个？

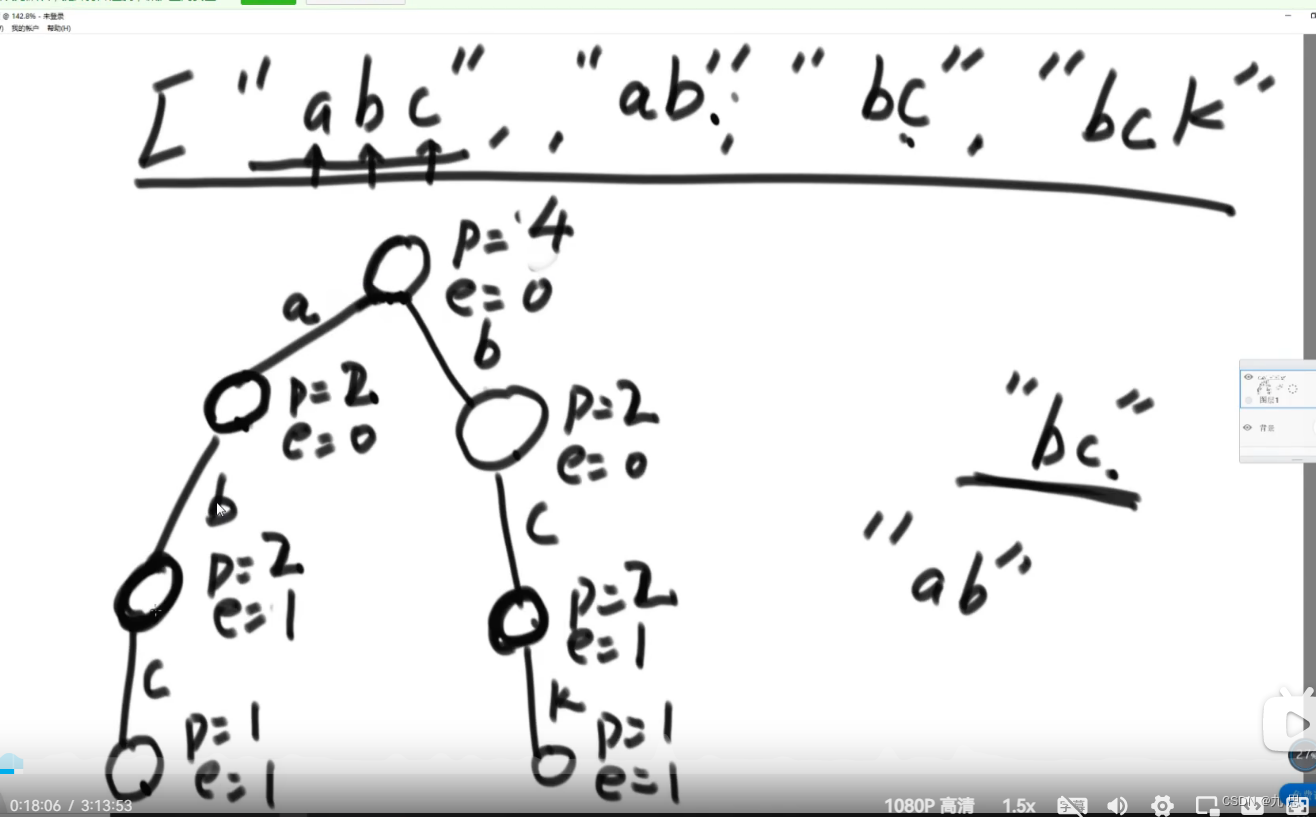
如何生成前缀树：字典节点有两个值pass和end，pass代表有几个字符串通过了当前节点，end代表有几个字符串以该节点为结束节点。对于每一个字符串来说，从头结点开始，头结点上P每添加一个字符串就+1。判断头结点通向下一个节点的路上有没有第一个字母，如果有，就复用；如果没有，就新建一条路，路上标记这个字母，并且在经过的节点的p+1。然后判下一个字符有没有存在的路，循环，直到最后一个字符标记完成，在最后经过的节点上的e+1。整个数组的字符串添加完成后，前缀树建立完成。

查询某个字符串是否出现过，只要走字符串长度的路就可以判断出来。

查询以“ab”为前缀的字符串有多少个，只要判断ab这条路的尾结点的p是多少就可以。

1.在实际代码里每个节点都包含一个26位的节点数组，来表示通往26个方向的路，如果为null，就是没有路，如果不为空，就是存在这条路。如果要表示的字符太多，比如汉字，可以用hashmap来存储:HashMap<Char,Node>，char存汉字，Node存路，即下一个节点。

2.每加入一个字符串，头结点的p都要+1，是代表所有字符串中以空字符串为前缀的个数。

贪心算法

在某一个标准下，可以想出来很多解题策略，优先考虑最满足标准的策略，最后考虑最不满足标准的策略，最终得到一个答案的算法，叫作贪心算法。

也就是说，不从整体最优上加以考虑，所做出的是在某种意义上的局部最优解。

局部最优 -> 整体最优

贪心就是蒙，看到题会有很多想法，用反证把一些先排除，然后对数器验证剩余想法结果正确性。
在笔试时千万不要去用数学方法验证想法正确性，因为太费时间了。贪心就是蒙，打worldfinal的同学也是先想出八九种策略，然后对数器，看哪一种正确，不过他们因为做过很多题，会总结出一些模板或者说做题方法 --左程云。

找时间总结一下贪心策略，但是不好总结。面试一般不出贪心，因为贪心主要看蒙没蒙对，看感觉，它的区分人才作用甚微。

贪心算法的在笔试时的解题套路

1，实现一个不依靠贪心策略的解法X，可以用最暴力的尝试

2，脑补出贪心策略A、贪心策略B、贪心策略C…

3，用解法X和对数器，去验证每一个贪心策略，用实验的方式得知哪个贪心策略正确

4，不要去纠结贪心策略的证明

证明贪心策略可能是件非常腌心的事情。平时当然推荐你搞清楚所有的来龙去脉，但是笔试时用对数器的方式

贪心策略在实现时，经常使用到的技巧：

1，根据某标准建立一个比较器来排序

2，根据某标准建立一个比较器来组成堆

都是用来找出规律，或者说找出每一步最绝对的选择

贪心题目

安排会议日程

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间(给你一个数组，里面是一个个具体的项目)，你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。返回这个最多的宣讲场次。

哪种会议结束时间早就先安排谁。按结束时间早进行排序，先安排结束最早的，然后把当前时间设置在这个会议的结束时候，然后看后边结束时间早并且开始时间大于等于当前时间的会议，循环直到所有会议都无法在继续安排。

因为每次选择结束时间最早的会议都能让留给剩下开会的时间最多。

切金条

一块金条切成两半，是需要花费和长度数值一样的铜板的。比如长度为20的金条，不管切成长度多大的两半，都要花费20个铜板。

一群人想整分整块金条，怎么分最省铜板?

例如,给定数组{10,20,30}，代表一共三个人，整块金条长度为10+20+30=60。 金条要分成10,20,30三个部分。 如果先把长度60的金条分成10和50，花费60； 再把长度50的金条分成20和30，花费50；一共花费110铜板。 但是如果先把长度60的金条分成30和30，花费60；再把长度30金条分成10和20， 花费30；一共花费90铜板。

输入一个数组，返回分割的最小代价。

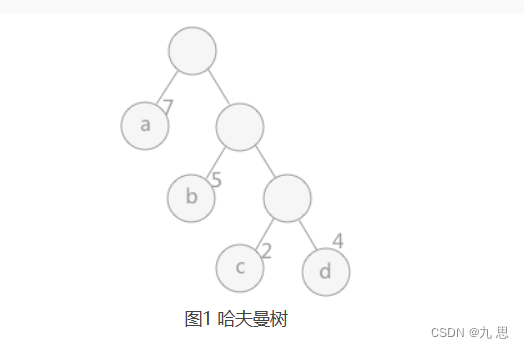
这题是构建哈夫曼树。

先切出来最大的，然后在依次切比较小的，这样花费的铜块最少。逆向思考，把所有数字放进小根堆，依次取出两个值，把这两个值加起来，结果加到result里，并且把这个和扔到小根堆里。循环，直到小根堆里取出最后两个数。

每次切割都切割出来当前需要的最大的，相当于每次找出最大的节点，让他的加权最小。

什么是哈夫曼树?

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。

在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。在图 1 中，因为结点 a 的权值最大，所以理应直接作为根结点的孩子结点。

做项目赚最多钱

输入：

正数数组costs

正数数组profits

正数k

正数m

含义：

costs[i]表示i号项目的花费

profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润)

k表示你只能串行的最多做k个项目

m表示你初始的资金

说明：

你每做完一个项目，马上获得的收益，可以支持你去做下一个项目。

输出： 你最后获得的最大钱数。

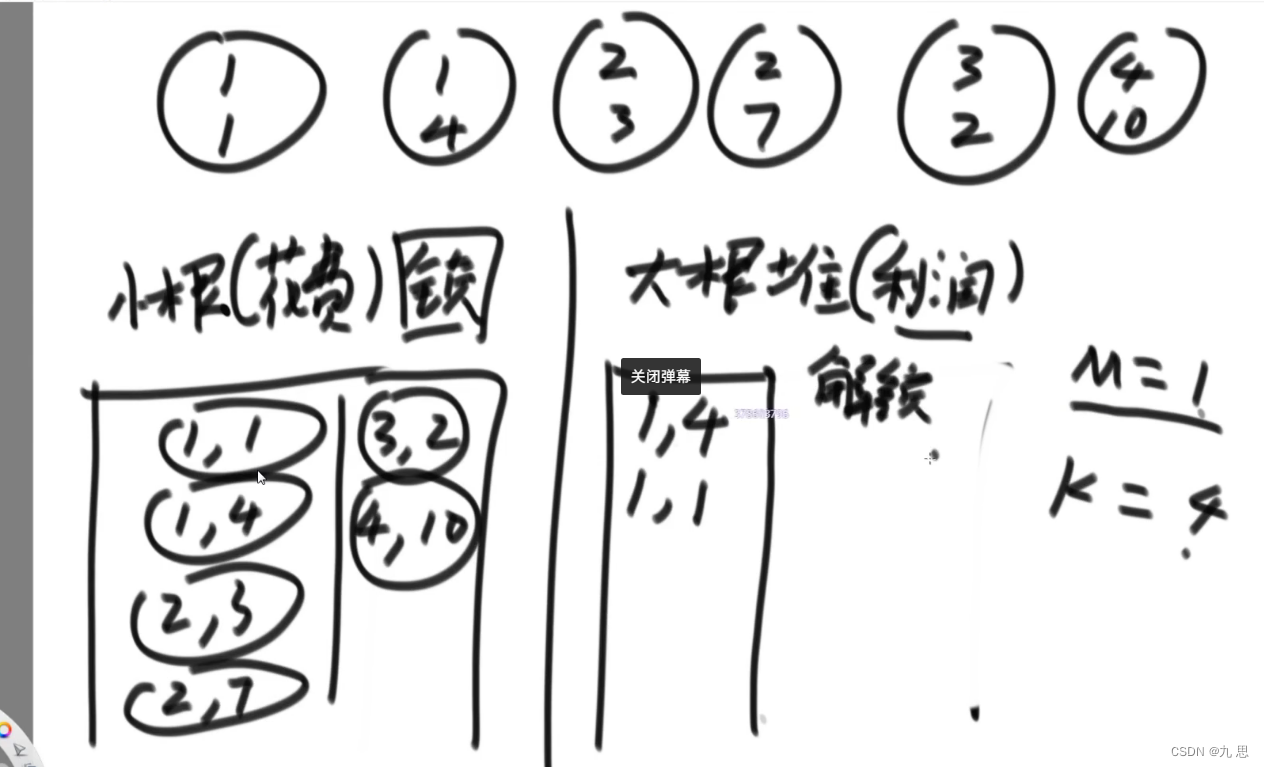
做完项目后的钱等于利润+投入资金，即项目总收入。

本题需要一个小根堆和一个大根堆。小根堆里先把所有项目存进去，按照投入资金排序。每次弹出所需资金小于等于当前拥有资金的项目，到大根堆里，大根堆按照利润排序，然后让大根堆弹出根节点，即当前获利最大的项目，去做这个项目，然后该项目利润加到结果里。然后进行第二次循环，最后直到项目次数到达k或者项目被挨个做了一遍。

一个数据流中，随时可以取得中位数

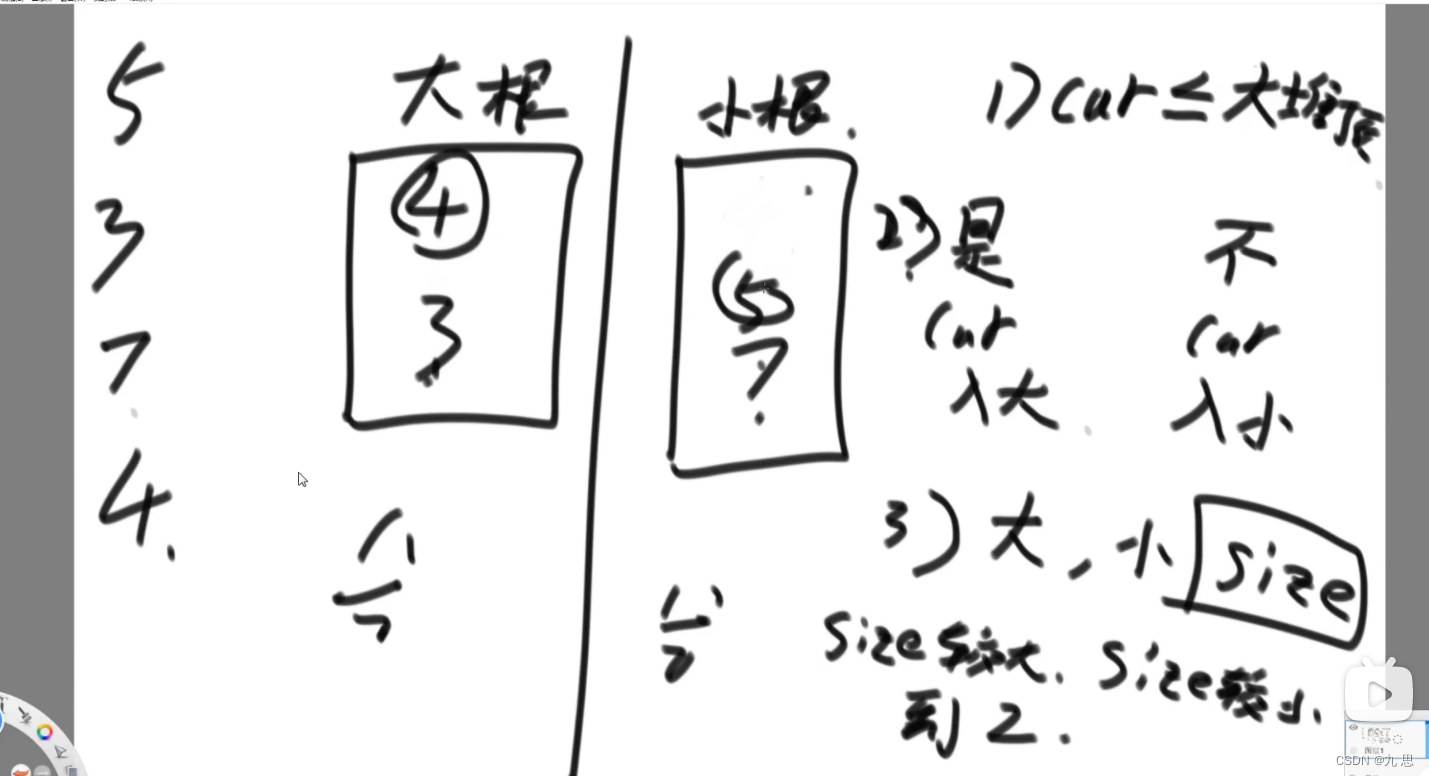
维护一个大根堆和一个小根堆，大根堆维护中位数左边的值，小根堆维护中位数右边的值。

第一个数直接进大根堆，之后每次插入一个数的时候，判断当前数字是否小于等于大根堆，如果是，就放入大根堆，如果不是，放入小根堆，插入之后判断大根堆和小根堆的大小，如果某一个堆的大小大于另一个堆到了2个，就把size大的根节点弹出到size小的堆。然后时刻都能获取中位数，如果其中一个比另一个多一个节点，那就是size大的堆的根节点；如果size相同，那么两个根节点相加除二。

基础08(暴力递归)

暴力递归

暴力递归就是尝试

1，把问题转化为规模缩小了的同类问题的子问题

2，有明确的不需要继续进行递归的条件(base case)

3，有当得到了子问题的结果之后的决策过程

4，不记录每一个子问题的解。

一定要学会怎么去尝试，因为这是动态规划的基础，这一内容我们将在提升班讲述

递归就是要把大问题化解为子问题，只要把子问题处理好，大问题就能解决。要注意，不要着重考虑全局流程是怎么样的，那样容易想不明白，正确的应该是把子问题想清楚，其他的让递归去解决。

汉诺塔

打印n层汉诺塔从最左边移动到最右边的全部过程

算法思路：汉诺塔使用递归解决，比如现在有从上到下1_{i个圆盘，不要考虑“左”“中”“右”这些概念，而是把三根柱子理解为start、end、other。要把i盘子放到end位置，就需要先把1}i-1的盘子移动到other上，然后把i从start移动到end。这时候1~i-1这些盘子其实是在other上，现在要把这些盘子移动到end上，那么start、end、other这些概念就有了变化，现在的start就应该是之前的other，end还是end，other是原来的start，如此递归直到最后一个盘子（即1盘子）移动到最右边的柱子上—这是base case，有了第一根移动到右边，才可以返回递归的结果，从而让2、3、……、i 递归成功。

代码：

public class Code01_Hanoi {

	public static void hanoi(int n) {
		if (n > 0) {
			func(n, n, "left", "mid", "right");
		}
	}

    //rest：控制base case和2~i盘子的输出  down：代表现在处理的盘子 from：起始地 help：other柱子 to：目的地 
	public static void func(int rest, int down, String from, String help, String to) {
		if (rest == 1) {
			System.out.println("move " + down + " from " + from + " to " + to);
		} else {
			func(rest - 1, down - 1, from, to, help);//先把自己上边的盘子全移过去，移到help柱子上
			func(1, down, from, help, to);//从这里可以看出来rest的作用可以控制打印，这个处理相当于就是移动i到右柱子
			func(rest - 1, down - 1, help, from, to);//当i移到右柱子后，需要把1~i-1的盘子，还原到左柱子上
		}
	}

	public static void main(String[] args) {
		int n = 3;
		hanoi(n);
	}

}

N皇后

N皇后问题是指在N*N的棋盘上要摆N个皇后，要求任何两个皇后不同行、不同列，也不在同一条斜线上。 给定一个整数n，返回n皇后的摆法有多少种。

n=1，返回1。

n=2或3，2皇后和3皇后问题无论怎么摆都不行，返回0。

n=8，返回92。

这道题使用暴力递归，时间复杂度为O(N的N次方)，不过题目里给的皇后个数一般都很少，N皇后基本之能这样做，不过下面的优化也可以给速度带来很大提升。

这道题就是逐个遍历，每放下一个皇后就在record数组里记下放的位置，（record数组用下标代表是哪个皇后，值表示放的位置），在放第二个皇后就放在下一行，然后判断哪些位置放下去后不违规。对于行上的限制，基本不用判断，因为每个皇后独占一行，一共N行。对于列，需要看record的值里有没有这条列被记录。对于斜线，让两位置的行下标相减的绝对值和列下标相减绝对值相比，如果相等，说明是45度角，说明在通一条直线上，那就违规了。

代码：

public static int num1(int n) { 
		if (n < 1) {
			return 0;
		}
		int[] record = new int[n];//数组下标代表皇后，值代表放在第几列
		return process1(0, record, n);
	}

	public static int process1(int i, int[] record, int n) {
		if (i == n) { //base case
			return 1;
		}
		int res = 0;
		for (int j = 0; j < n; j++) { //判断该行的每一列是否合法
			if (isValid(record, i, j)) { //如果合法，设置该行皇后的位置，并且进行下一行的判断
				record[i] = j;
				res += process1(i + 1, record, n);
			}
		}//整个棋盘判断完后不用设置record初始化，因为每次判断是否合法都是判断该行之前的棋盘，而且之前行的record都是本轮的结果
		return res;
	}

	public static boolean isValid(int[] record, int i, int j) {//record：皇后位置的记录 i：第几行 j：第几列
		for (int k = 0; k < i; k++) {
			if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
				return false;
			}
		}
		return true;
	}

N皇后优化

虽然该优化没有改变时间复杂度，但是通过位运算表示位置信息让该题目优化提升非常大。

主要是利用位运算表示皇后的摆放，并且用位信息表示之前摆放的皇后对当前皇后的影响，每一步基本都是位运算，设计非常巧妙。

代码：

public static int num2(int n) { //n不能超过32
		if (n < 1 || n > 32) {
			return 0;
		}
		int upperLim = n == 32 ? -1 : (1 << n) - 1;//用来限制皇后可放最大列数，易知每个数二进制最左的左边是0，用来限制高位
		return process2(upperLim, 0, 0, 0);
	}

	//最大限制（全局不会变），列限制，左斜线限制，右斜线限制
	public static int process2(int upperLim, int colLim, int leftDiaLim, int rightDiaLim) {
		if (colLim == upperLim) {//base case
			return 1;
		}
		int pos = 0;
		int mostRightOne = 0;
		pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim)); //把列和左斜线右斜线限制合到一起，然后再和最大限制与运算，位上为1的可以防止，位上为0的不可以放置
		int res = 0;
		while (pos != 0) {
			mostRightOne = pos & (~pos + 1); //取出二进制最右的1，while循环可以遍历所有的可行位置
			pos = pos - mostRightOne;//让下一次循环就没有上次最右边的1了
			res += process2(upperLim, colLim | mostRightOne,//最右边有皇后了，需要在列限制上加上这个位置
					(leftDiaLim | mostRightOne) << 1, //左斜线限制左移1代表下一行的左斜线限制
					(rightDiaLim | mostRightOne) >>> 1);//同上
		}
		return res;
	}

打印一个字符串的全部子序列，包括空字符串

算法思路：对于每一个字符，都有选择和不选择两种情况，在遍历到一个字符时，进行选择就行了，递推到字符串结束时，打印出来。可以理解整个流程想象为一个二叉树，每个节点代表一个字符，左右孩子代表选择或者不选择该字符。

未优化代码：未优化的代码会创建许多数组，有些浪费空间，而且复制数组的操作并不轻便

public static void function(String str) {
		char[] chs = str.toCharArray();//转化为字符数组
		process(chs, 0, new ArrayList<Character>());
	}
	//i表示当前递归走到了哪一个字符 res表示之前的字符选择
	public static void process(char[] chs, int i, List<Character> res) {
		if(i == chs.length) {//base case
			printList(res);
		}
		List<Character> resKeep = copyList(res);//复制之前的选择
		resKeep.add(chs[i]);//选择当前字符的选项
		process(chs, i+1, resKeep);//对新数组进行操作，并不用考虑进一步的操作对原数组的影响
		List<Character> resNoInclude = copyList(res);//新建另一个数组，代表不选择当前字符的选项
		process(chs, i+1, resNoInclude); //打印完之后，整个方向就结束了
	}

	public static void printList(List<Character> res) {
		// ...;
	}

	public static List<Character> copyList(List<Character> list){
		return null;
	}

优化后代码：优化后没有数组的复制，前后只用了一个数组

public static void printAllSubsquence(String str) {
		char[] chs = str.toCharArray();
		process(chs, 0);
	}

	public static void process(char[] chs, int i) {
		if (i == chs.length) {
			System.out.println(String.valueOf(chs));
			return;
		}
     //选择该字符
		process(chs, i + 1);
     //不选择该字符
		char tmp = chs[i];//储存住字符以便恢复
		chs[i] = 0;//ascll编码为0代表null，不打印，也就是不选择该字符
		process(chs, i + 1);
		chs[i] = tmp;//恢复数组，保证返回到上层调用时数组不变化
	}

打印一个字符串的全部排列

打印一个字符串的全部排列，要求不要出现重复的排列

这个和前边的不一样，前边的打印结果都是按顺序的，现在这个字符的顺序可以变换,比如abc有abc,acb,bac,bca,cab,cba 6种情况。

算法思路：中心思想，一个字符串，在遍历到每一位置上的时候，他后面的字符每一个都可以替代他，让所有后面的字符都替代他一次那么，这个位置上的所有情况就都遍历出来了。这个字符之前的都相当于是确定的，不能再动的。接着递归到下一个字符，循环知道字符串结尾。

要求不要出现重复的排列：在对一个字符进行判断时，他后边的某个字符可能会和他一样，比如都是“a”字符，这种情况就不用再替换了，因为排序都一样，这是剪枝做法。

代码：

	public static ArrayList<String> Permutation(String str) {
		ArrayList<String> res = new ArrayList<>();//这个数组用来储存所有的结果--结果集
		if (str == null || str.length() == 0) {
			return res;
		}
		char[] chs = str.toCharArray();
		process(chs, 0, res);
		res.sort(null);//这一步是题目扩展，对字符集结果进行排序
		return res;
	}

	//chs：字符数组，全局就这一个数组，节省空间 i:当前判断到了哪一个字符 res：结果集
	public static void process(char[] chs, int i, ArrayList<String> res) {
		if (i == chs.length) {//base case 
			res.add(String.valueOf(chs));//添加这种情况到结果集
		}
		boolean[] visit = new boolean[26];//每个递归层级都有一个这样的数组，用来避免重复的字符进行位置交换
		for (int j = i; j < chs.length; j++) { //遍历当前字符后边的所有字符，如果没有和这种字符进行交换过，那就符合要求可以交换
			if (!visit[chs[j] - 'a']) {
				visit[chs[j] - 'a'] = true;
				swap(chs, i, j);
				process(chs, i + 1, res);//递归判断下一位
				swap(chs, i, j);//回溯还原场景，方便上层递归的下一次循环
			}
		}
	}

	public static void swap(char[] chs, int i, int j) {
		char tmp = chs[i];
		chs[i] = chs[j];
		chs[j] = tmp;
	}

翻转栈

给你一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。如何实现?

算法思路：不能使用额外的数据结构，我们选择在递归中利用系统栈储存上层递归产生的信息。大体思路是需要一个f方法，弹出并返回当前栈底元素，弹出的元素保存在系统栈里，也就是上层递归的临时变量里。循环直到栈中元素为空，然后从最下层递归依次把所有元素压入栈中，最终使元素逆序。本题代码里使用了“递归的递归”。

代码：

public static void reverse(Stack<Integer> stack) {//从始至终只用了这个栈
		if (stack.isEmpty()) {
			return;//当栈里的元素全部弹出后，说明下一步就要开始把i变量压入栈里了
		}
		int i = getAndRemoveLastElement(stack);//弹出并返回当前栈底元素，保存在临时变量里
		reverse(stack);//进行下一层的递归
		stack.push(i);//把储存在系统栈里的元素压入栈，最先压入的是原先栈的栈顶元素
	}

	public static int getAndRemoveLastElement(Stack<Integer> stack) {//弹出并返回当前栈底元素
		int result = stack.pop();//弹出栈顶
		if (stack.isEmpty()) {//base case
			return result;//返回栈底
		} else {
			int last = getAndRemoveLastElement(stack);//得到下一个栈顶，即当前元素的下面的元素
			stack.push(result);//还原栈结构，待整个getAndRemoveLastElement方法结束后，栈少了一个栈底元素，其他都应该保持不变
			return last;
		}
	}

字符串转化

规定1和A对应、2和B对应、3和C对应… 那么一个数字字符串比如"111"，就可以转化为"AAA"、“KA"和"AK”。 给定一个只有数字字符组成的字符串str，返回有多少种转化结果。转化

算法思路：对于每一个遍历到的元素，除了0，都可以让自己或者和自己的下一个组成一个数字，并转化为字符，0的后面即使是“01”“02”“011”，也不能转化为字符，因为字符串中多了0，和单纯的1是不一样的。对每个字符进行两个判断，是自身，还是自身和后边的字符组合。当自身是1时，和后面的所有都可以组合；当自身是2时，后面只能是0-6，当自己是其他时都不符合。

	public static int number(String str) {
		if (str == null || str.length() == 0) {
			return 0;
		}
		return process(str.toCharArray(), 0);
	}

	public static int process(char[] chs, int i) {
		if (i == chs.length) {//base case 转化方式+1
			return 1;
		}
		if (chs[i] == '0') {//0什么都不能转化
			return 0;
		}
		if (chs[i] == '1') {
			int res = process(chs, i + 1);//只自身转化
			if (i + 1 < chs.length) {//判断后面的字符可不可以和自己组合
				res += process(chs, i + 2);//组合转化
			}
			return res;
		}
		if (chs[i] == '2') {//自身是2的情况
			int res = process(chs, i + 1);
			if (i + 1 < chs.length && (chs[i + 1] >= '0' && chs[i + 1] <= '6')) {
				res += process(chs, i + 2);
			}
			return res;
		}
		return process(chs, i + 1);
	}

袋子里装最多价值的东西

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表 i号物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？

算法思路：暴力递归，对于遍历到的每一个物品，都可以选择要或者不要，在要和不要分别进行两个递归，取递归结果最大的那个。在不超重的情况下，选价值最多的那个递归路线。

代码：

public static int maxValue1(int[] weights, int[] values, int bag) {
    return process1(weights, values, 0, 0, bag);
}
public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
	if (alreadyweight > bag) {
		return 0;
	}
	if (i == weights.length) {
		return 0;
	}
	return Math.max(

			process1(weights, values, i + 1, alreadyweight, bag),

			values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
}

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸 牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A 和玩家B都绝顶聪明。请返回最后获胜者的分数。

【举例】

1、arr=[1,2,100,4]。

开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，接下来 玩家 B可以拿走2或4，然后继续轮到玩家A… 如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继 续轮到玩家A… 玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1， 让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家 A拿走。玩家A会获胜， 分数为101。所以返回101。

2、arr=[1,100,2]。 开始时，玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜， 分数为100。所以返回100。

算法思路：暴力递归，在每次选择的时候都分先手和后手，在我先手的时候是我先选牌，我需要选择“当前选的牌加上后手递归结果”中较大的递归路线，在我后手的时候，我获得的都是较小的那张牌，因为对手选的是左右边上最大的牌，这样就能保证所有选择都能暴力尝试，最终选择出最大的结果。

我每次选择都要保证我选择的牌加上递归结果是最大的，对手选择时都要保证我选择的牌都是最小的，正好相反，这是题干中“聪明绝顶”要求的体现。

代码：

public static int win1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));//选择先手和后手中最大的
	}

	public static int f(int[] arr, int i, int j) {//先手函数
		if (i == j) {
			return arr[i];
		}
		return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));//返回“当前选择的牌+递归结果”中最大的
	}

	public static int s(int[] arr, int i, int j) {
		if (i == j) {
			return 0;
		}
		return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));//对手分别选择最左边和最右边的两个选择，这些选择中对手让我们不得不选择最小的值
	}

袋子里装最多价值的东西

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表 i号物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？

算法思路：暴力递归，对于遍历到的每一个物品，都可以选择要或者不要，在要和不要分别进行两个递归，取递归结果最大的那个。在不超重的情况下，选价值最多的那个递归路线。

代码：

public static int maxValue1(int[] weights, int[] values, int bag) {
    return process1(weights, values, 0, 0, bag);
}
public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
	if (alreadyweight > bag) {
		return 0;
	}
	if (i == weights.length) {
		return 0;
	}
	return Math.max(

			process1(weights, values, i + 1, alreadyweight, bag),

			values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
}

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸 牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A 和玩家B都绝顶聪明。请返回最后获胜者的分数。

【举例】

1、arr=[1,2,100,4]。

开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，接下来 玩家 B可以拿走2或4，然后继续轮到玩家A… 如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继 续轮到玩家A… 玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1， 让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家 A拿走。玩家A会获胜， 分数为101。所以返回101。

2、arr=[1,100,2]。 开始时，玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜， 分数为100。所以返回100。

算法思路：暴力递归，在每次选择的时候都分先手和后手，在我先手的时候是我先选牌，我需要选择“当前选的牌加上后手递归结果”中较大的递归路线，在我后手的时候，我获得的都是较小的那张牌，因为对手选的是左右边上最大的牌，这样就能保证所有选择都能暴力尝试，最终选择出最大的结果。

我每次选择都要保证我选择的牌加上递归结果是最大的，对手选择时都要保证我选择的牌都是最小的，正好相反，这是题干中“聪明绝顶”要求的体现。

代码：

public static int win1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));//选择先手和后手中最大的
	}

	public static int f(int[] arr, int i, int j) {//先手函数
		if (i == j) {
			return arr[i];
		}
		return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));//返回“当前选择的牌+递归结果”中最大的
	}

	public static int s(int[] arr, int i, int j) {
		if (i == j) {
			return 0;
		}
		return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));//对手分别选择最左边和最右边的两个选择，这些选择中对手让我们不得不选择最小的值
	}