学习笔记1:三大聚类方法:K-means聚类、层次聚类、DBSCAN聚类
前言
在样本数量较多的情况下,可以通过聚类将样本划分为多个类,对每个类中单独使用模型进行分析和相关运算,亦可以探究不同类之间的相关性和主要差异。
例如Mathor Cup 2022年D题
此外,可以借助https://www.naftaliharris.com/blog/visualizing-k-means-clustering/来可视化聚类
一、K-means聚类
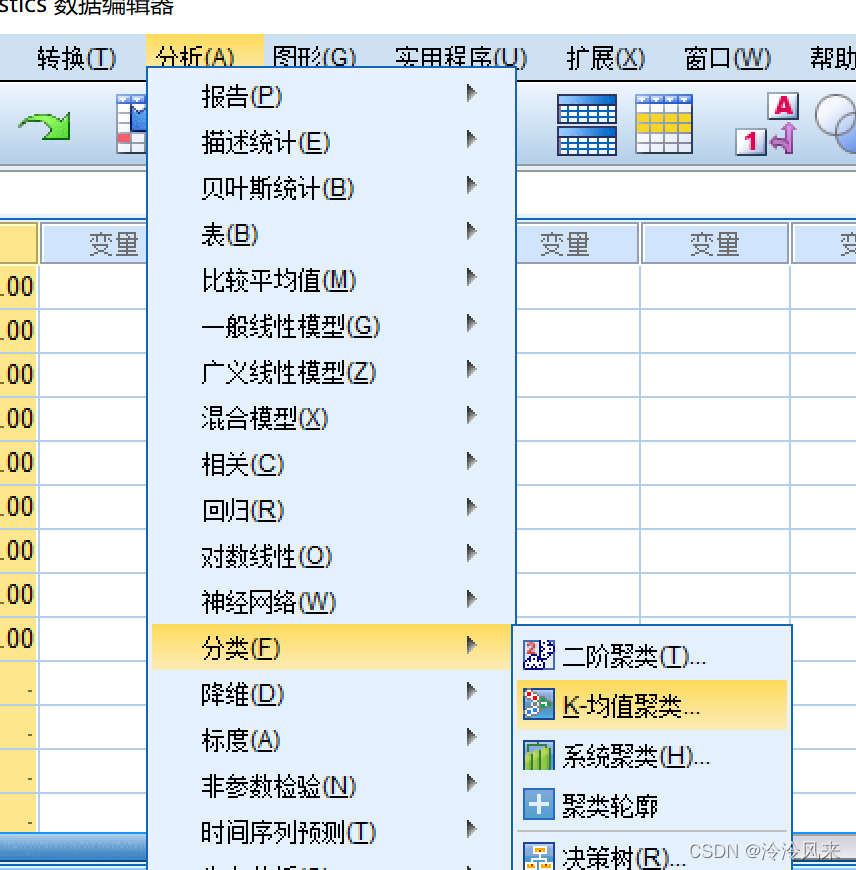
一般而言,K-means聚类采用SPSS会更加快捷方便。故对于该算法接下来采用SPSS来说明如何使用。
- 指定需要划分的类的个数,即K值
- 选择K个数据对象作为初始聚类中心。实际上我们可以自己选择开始的聚类中心和结束时的聚类中心,也可以选择迭代得到较好的聚类中心
- 计算各个数据对象到这K个聚类中心的距离,并据此归类
- 不断重复2.3两个步骤,得到较优的聚类结果。可以直接划分类别,仅分类而不迭代
可以看到,这个方法的一个短板在于需要自己得到K的个数
操作过程
-
-
对K-means聚类中的各参数说明
此处有关于该聚类方法的详细说明
举个例子,在对一个班级之间学生成绩进行聚类时,学生就是“个案标注依据”,各科成绩就是“变量”。倘若遇到变量量纲不一致的情况,我们可以先进行标准化再进行聚类。
分析>>描述统计>>描述>>将标准化值另存为变量 -
在SPSS中加入初始聚类中心时我们可以先利用SPSS导出我们所需要的聚类中心,保存为.sav格式即可。
二、层次聚类
通过计算两类数据点之间的距离,对最接近的两类数据点进行合并,并且反复迭代这一过程知道所有的数据点合成一类生成 谱系图
层次聚类中,谱系图十分实用,可以通过观察谱系图来自行分类。当然,该聚类方法已经帮你分了很多小类并且计算出了各个类别之间的距离。
操作过程
同上述K-means聚类,选择系统聚类即可(电脑截图出故障了,图先不放了)
在层次聚类中可以选择类与类之间的聚类方法和点与点之间的聚类方法,可以勾选谱系图
<肘部法则:通过畸变系数来确定类的个数>
三、DBSCAN聚类
DBSCAN算法即基于密度的算法,该算法生成类别的个数由样本决定,将一定空间内所包含的对象归为一类,需要确定聚类半径和包含点。(可以将该算法理解为,通过以某一个数据点为圆心,以所确定的聚类半径为半径画圆,数其中所包含的点,如果包含的点达到要求,就认为它是核心点,并且以它周围的点为圆心,不断重复这个过程)
该算法对于某些异常点并不敏感,可以通过这个算法去除异常点。
操作过程
matlab代码(需要用到一个新的函数dbscan,某些版本的matlab可能无法使用)
epsilon=R;%半径
minpts=N;%包含点
idx = dbscan([x,y],epsilon,minpts);
length(unique(idx));%聚类数
倘若我们需要查看某类中包含的样品点
find(idx==n);%n为第几类
%所得到的返回值为样本位于原样本的行数和该类总样本数
倘若想知道每个类别中包含多少个样品点
[gc,grps] = groupcounts(idx);%其中gc为每一类对应的个数,grps为类别
为了方便剔除孤立点,我们可以对类进行排序
sortrows([gc,grps],'descend');%降序排列
%但是sortrows的用法远不止于此,其可以对某列或者某几列进行单独的排序
对结果进行可视化
figure('Name','DBSCAN聚类结果','NumberTitle','off');
gscatter(x,y,idx,[],[],1,'doleg','off');
xlabel('');ylable('');
总结
根据题目要求和个人需要选择使用某种聚类方法,抑或是多种结合使用。