聚类(clustering)学习简介
聚类学习是机器学习领域中的一个重要分支,其主要目标是将未知标签数据集中的样本分成不同的组别(簇),使得同一组内的样本相似度较高(物以类聚),而不同组之间的相似度较低(分类)。聚类分析有助于识别数据中的规律、模式、结构和群体,并对无监督学习问题提供有价值的信息。
1. 基本概念
-
相似度度量: 聚类算法通常使用相似度度量(如欧氏距离、余弦相似度等)来评估样本之间的相似程度。
将相似的样本聚集在一起,使得同一类簇的样本尽可能接近,不同类簇的样本尽可能远离。对于“距离度量”,满足一些基本性质:
-
聚类算法: 常见的聚类算法包括K均值聚类、层次聚类、DBSCAN(基于密度的聚类)等。
2. 常见聚类算法
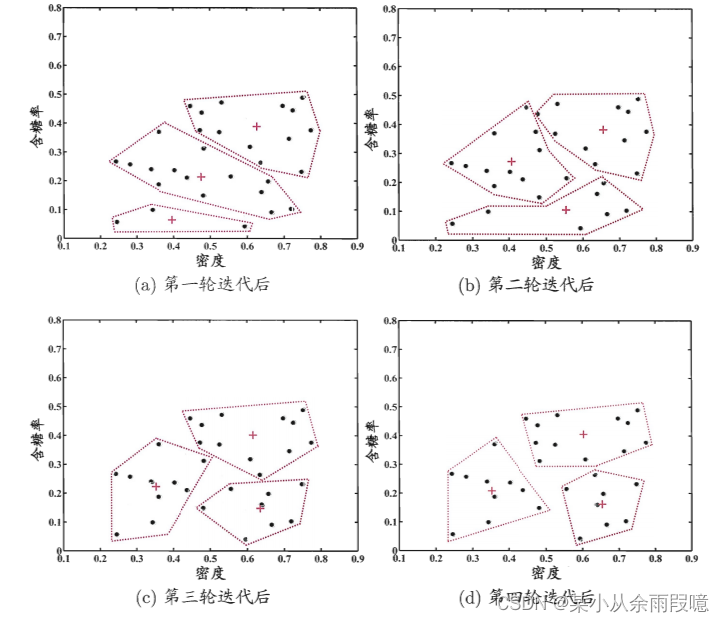
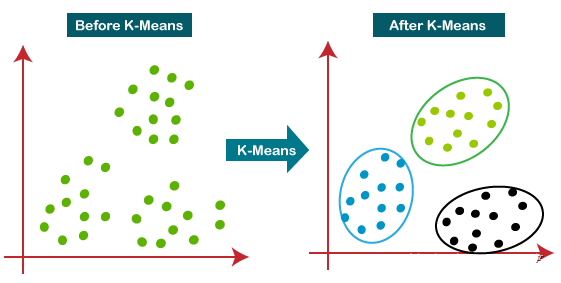
2.1 K均值聚类(k-means clustering)
K均值聚类是一种常用的无监督学习算法,用于将数据集中的样本划分为K个不同的簇,使得每个样本属于离其最近的簇中心。该算法被广泛应用于数据分析、图像处理和模式识别等领域。
原理:
将样本分成K个簇,使得每个样本与其所属簇的中心点的距离最小化:
-
簇中心初始化: 随机选择K个样本作为初始的簇中心。
-
样本分配: 将每个样本分配到离其最近的簇中心所对应的簇。
-
更新簇中心: 对每个簇,计算其所有样本的均值,将该均值作为新的簇中心。
-
迭代: 重复进行样本分配和簇中心更新,直到收敛(簇中心不再改变)或达到预定的迭代次数。

算法步骤:
- 随机初始化K个簇的中心点。
- 将每个样本分配到最近的簇。
- 更新每个簇的中心点。
- 重复2-3步骤,直到收敛或达到预定迭代次数。
K均值聚类是一种简单而有效的聚类算法,特别适用于对数据集进行分组的场景。然而,它对初始值和K值的选择较为敏感,因此在使用时需要考虑这些因素以获得更好的聚类效果。
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 生成模拟数据
data, labels = make_blobs(n_samples=300, centers=4, random_state=42)
# 创建K均值聚类模型
kmeans = KMeans(n_clusters=4, random_state=42)
# 拟合模型
kmeans.fit(data)
# 获取聚类结果
predicted_labels = kmeans.labels_
# 获取聚类中心
centroids = kmeans.cluster_centers_
# 可视化聚类结果和聚类中心
plt.scatter(data[:, 0], data[:, 1], c=predicted_labels, cmap='viridis', alpha=0.5)
plt.scatter(centroids[:, 0], centroids[:, 1], marker='X', s=200, linewidths=0.2, color='red')
plt.title('K-Means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()2.2 密度聚类
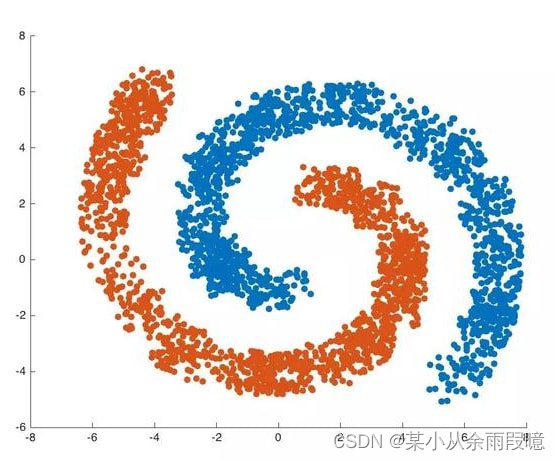
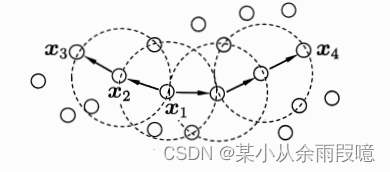
密度聚类是一种无监督学习算法,主要用于识别具有相对高密度的区域,并在数据集中发现任意形状的簇。其中,DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种著名的密度聚类算法。
DBSCAN算法步骤:
1 参数设置
- ε(Epsilon): 邻域半径,用于定义一个样本的邻域。
- MinPts: 最小样本点数,一个核心点所需的最小样本数。
2 算法步骤
- 随机选择一个未被访问的样本点。
- 如果该样本点的ε邻域内包含至少MinPts个样本点,标记为核心点。
- 以核心点为起点,通过密度可达性,找到所有密度可达的样本点,形成一个簇。
- 重复1-3步骤,直到所有样本点都被访问。
3 算法特点
- 核心点: 在ε邻域内包含至少MinPts个样本的点。
- 边界点: 不是核心点,但在某个核心点的ε邻域内。
- 噪音点: 既不是核心点也不是边界点。
3 优势与应用场景
- 适应任意形状的簇: DBSCAN不需要预先指定簇的数量,能够发现任意形状的簇。
- 鲁棒性: 对噪声和离群点具有较强的鲁棒性。
- 应用场景: 地理信息系统、图像分割、异常检测等。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
# 生成月亮形状的数据
data, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
# 创建DBSCAN聚类模型
dbscan = DBSCAN(eps=0.3, min_samples=5)
# 拟合模型
dbscan.fit(data)
# 获取聚类结果
predicted_labels = dbscan.labels_
# 可视化聚类结果
plt.scatter(data[:, 0], data[:, 1], c=predicted_labels, cmap='viridis', alpha=0.7)
plt.title('DBSCAN Clustering (Arbitrary Shape)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()2.3 层次聚类
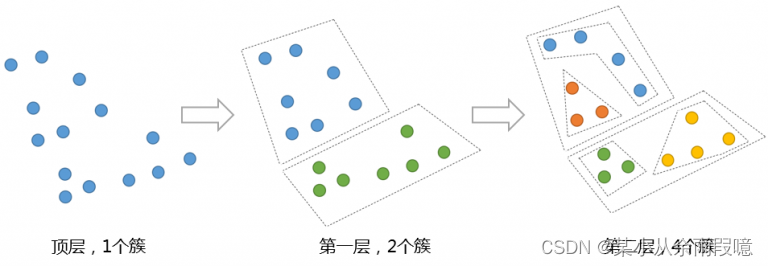
层次聚类是一种无监督学习算法,其主要目标是通过构建样本之间的层次结构将数据集中的样本分组。这种层次结构通常以树的形式表示,称为聚类树或树状图。层次聚类方法有两种主要类型:凝聚型和分裂型。
1. 凝聚型层次聚类
在凝聚型层次聚类中,首先将每个样本看作一个单独的簇,然后逐步合并具有最小距离的簇,直到达到预定的簇的数量或所有样本合并成一个簇。
算法步骤:
- 每个样本作为一个初始簇。
- 找到最近的两个簇,将其合并为一个新簇。
- 重复2步骤,直到达到预定的簇的数量或形成一棵层次树。
2. 分裂型层次聚类
在分裂型层次聚类中,首先将所有样本看作一个簇,然后逐步将簇分裂为子簇,直到每个样本都成为一个独立的簇。
算法步骤:
- 所有样本作为一个初始簇。
- 找到最不相似的样本,将其从簇中分离出去,形成一个新簇。
- 重复2步骤,直到每个样本都成为一个独立的簇或达到预定的簇的数量。
3 相似度度量
层次聚类的关键在于定义簇或样本之间的相似度。常用的相似度度量包括欧氏距离、曼哈顿距离、相关系数等。
层次聚类是一种强大而直观的聚类算法,通过构建层次结构揭示数据中的聚类关系。根据具体问题的要求,选择凝聚型或分裂型层次聚类,并合理选择相似度度量,可以得到对数据内在结构有深刻理解的聚类结果。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
# 生成模拟数据
data, labels = make_blobs(n_samples=300, centers=4, random_state=42)
# 创建凝聚型层次聚类模型
agg_clustering = AgglomerativeClustering(n_clusters=4, linkage='ward')
# 拟合模型
agg_clustering.fit(data)
# 获取聚类结果
predicted_labels = agg_clustering.labels_
# 可视化聚类结果
plt.scatter(data[:, 0], data[:, 1], c=predicted_labels, cmap='viridis', alpha=0.5)
plt.title('Agglomerative Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
# 绘制层次聚类的树状图
linked = linkage(data, 'ward')
dendrogram(linked, orientation='top', distance_sort='descending', show_leaf_counts=True)
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Sample Index', rotation = 70)
plt.ylabel('Distance')
plt.show()
最后,聚类学习是无监督学习的一个重要方向,通过对数据进行分组,揭示数据的内在结构。不同的聚类算法适用于不同类型的数据和问题,选择适当的算法和评价指标对于有效的聚类分析至关重要。
更多的资料可以参考西瓜书,吃瓜教程