目录
本文只是介绍如何使用 EViews,不包含任何的回归结果分析。
一、创建工作文件
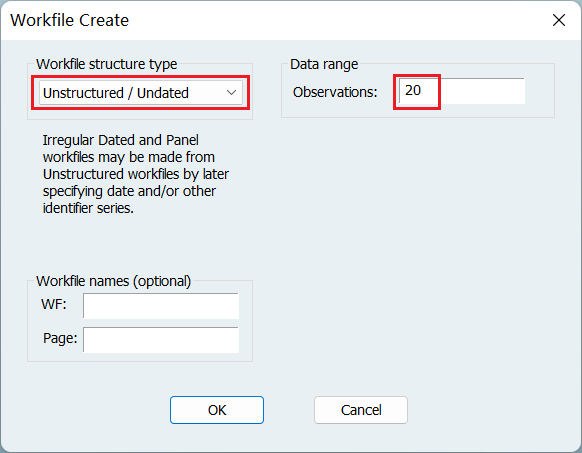
1、非时间序列数据
- 选择数据类型
- 填写样本数量
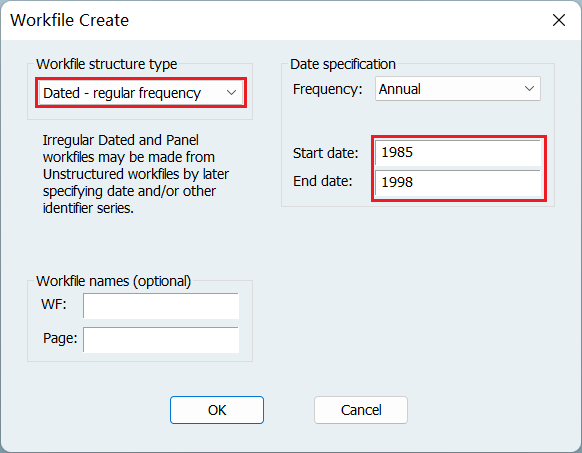
2、时间序列数据
- 选择数据类型
- 填写开始年份和截止年份
二、导入数据
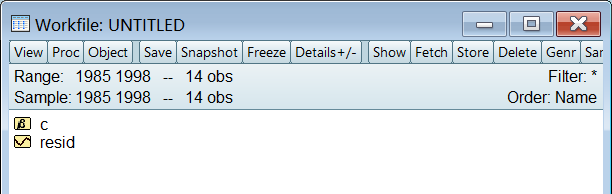
EViews 自带数据:
- c 是截距项
- resid 是残差
1、导入数据
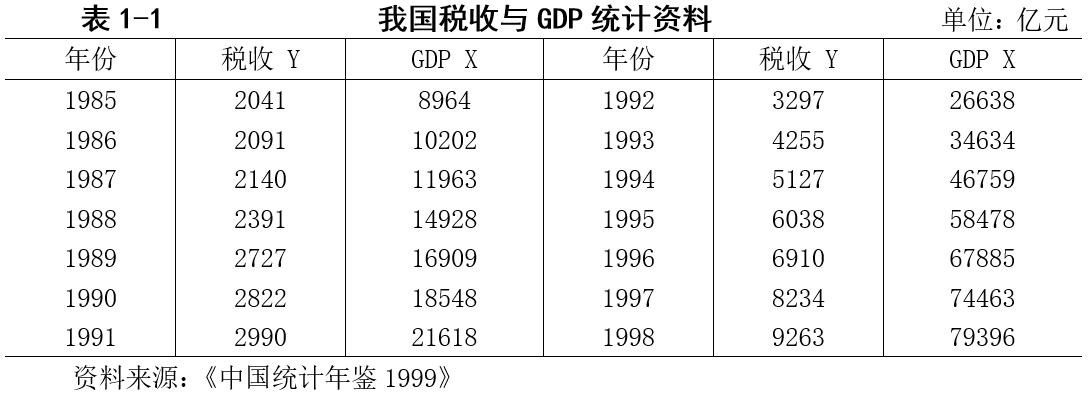
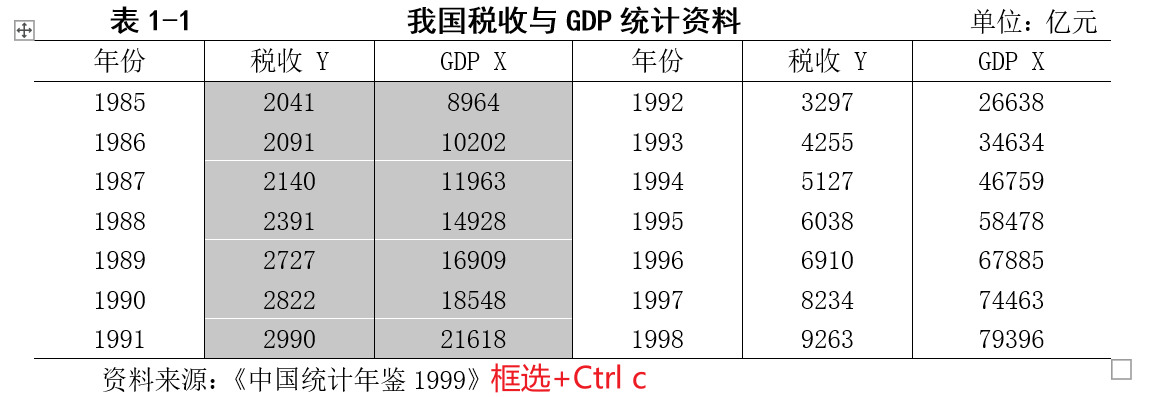
假设这是我们需要导入的数据:
在 EViews 中输入命令:
- y 对应税收 Y(名称自取,不一定非得是 y!)
- x 对应 GDP X(名称自取,不一定非得是 x!)
data y x得到如下弹框:
将数据复制粘贴进去,Word 或 Excel 都支持对框选的数据进行复制粘贴:
选中第一个框,直接 Ctrl+v,剩下的数据同理:
2、保存数据组合或方程结果
不管是保存数据组合还是保持方程结果,都是点这个 “name”:
至此你导入的数据和保存的数据组合如下图所示:
三、估计回归模型
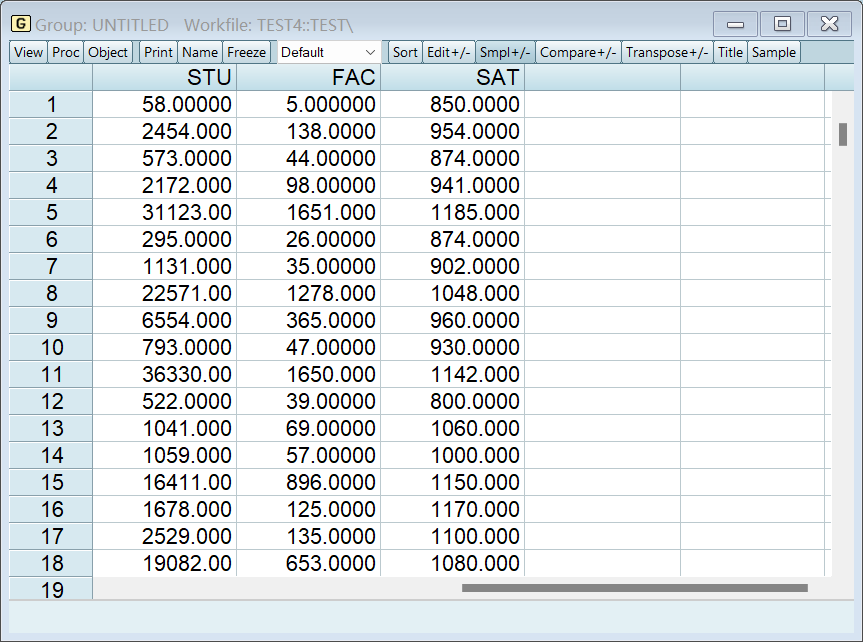
第一节用的数据太简单了,不方便展示,因此改用如下数据:
- 被解释变量:大学图书馆的藏书量(VOL)
- 解释变量:大学学生人数(STU)、大学教职工人数(FAC)、本科录取分数线(SAT)
1、估计回归模型
输入以下命令:
- ls 是指线性回归
- 必须以 c 间隔被解释变量和解释变量
- 解释变量之间没有先后顺序要求
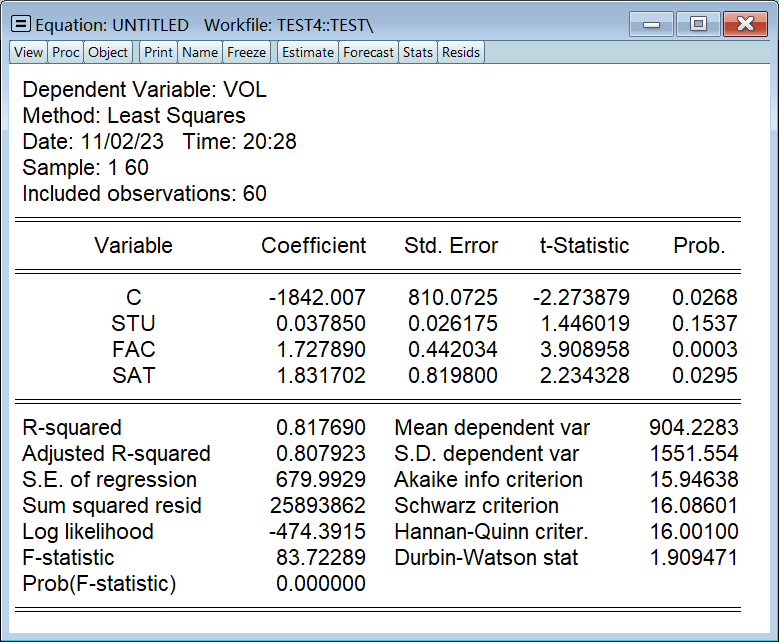
ls vol c stu fac sat得到回归模型:
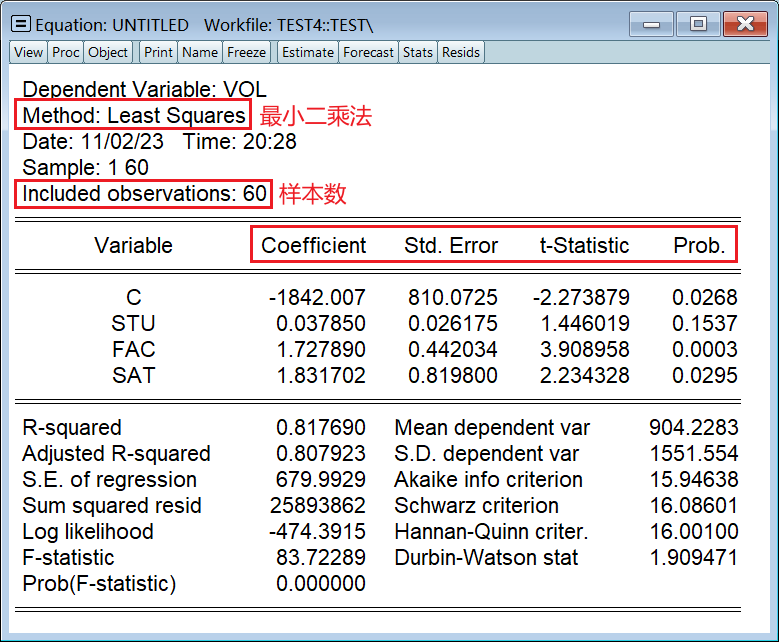
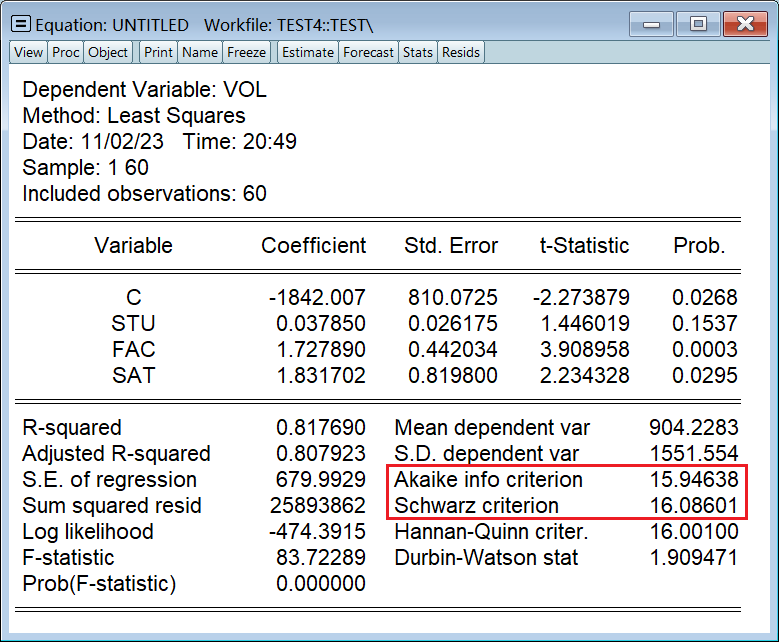
2、回归结果名词解读
第三个红框,从左到右依次是:
- 参数估计值
- 标准差
- t 统计量
- p 值
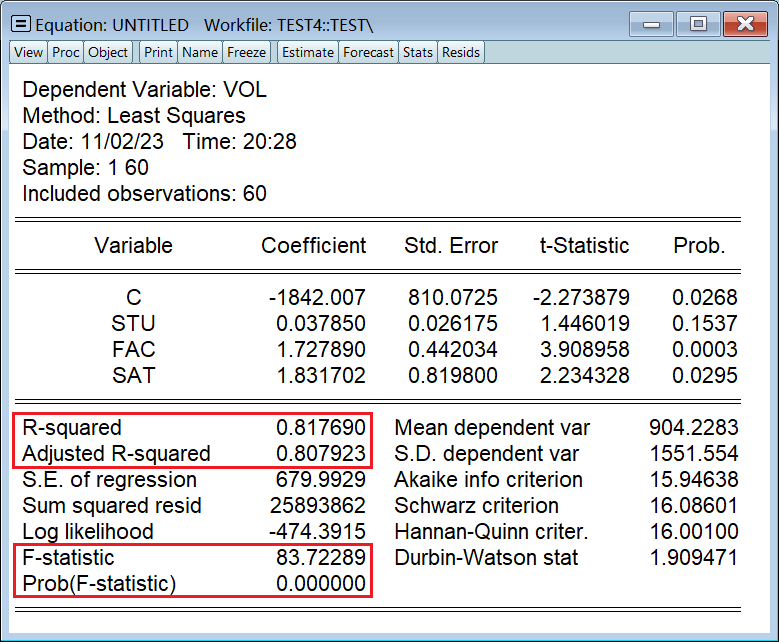
常用统计量,从上到下依次是:
- 拟合系数 R^2
- 调整后的拟合系数 R一把^2
- F 统计量
- p 值
四、检验模型设定错误
三大模型设定错误:
- 遗漏变量
- 加入了不相干变量
- 函数形式错误
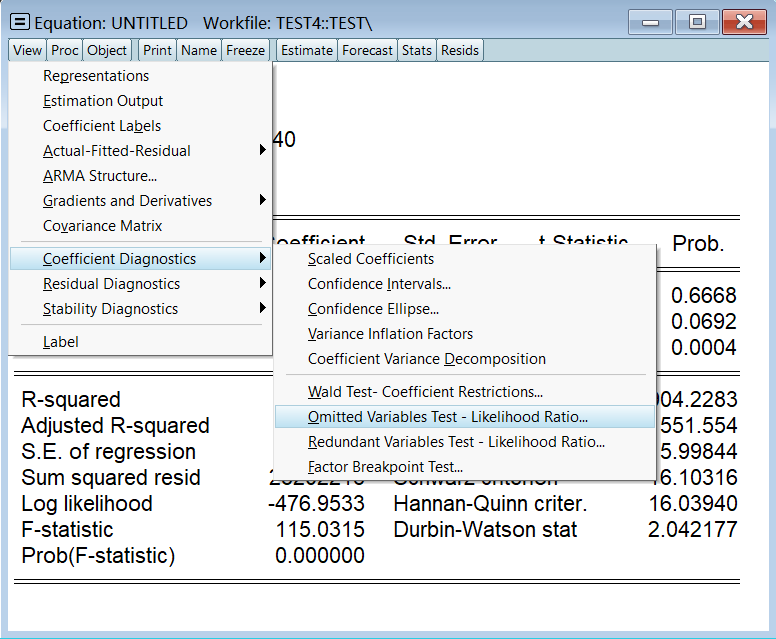
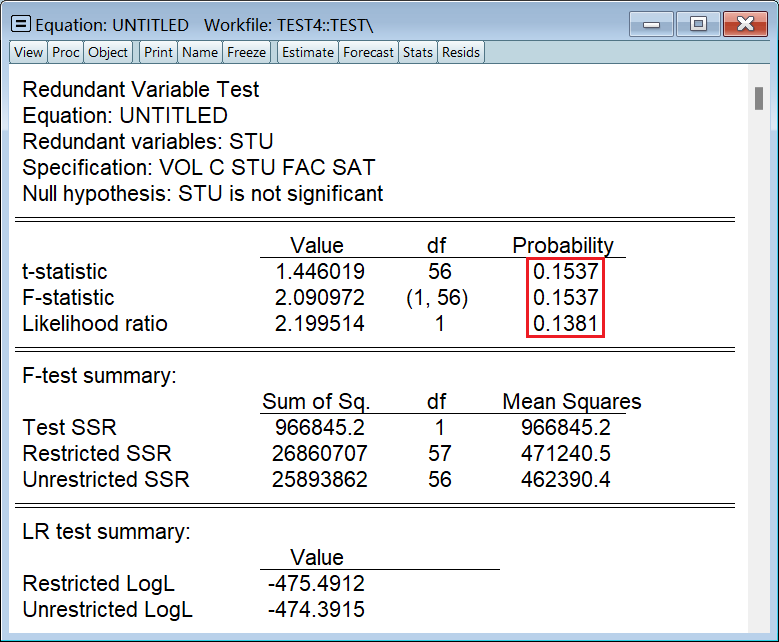
1、检验是否遗漏变量
假设我们不小心遗漏了变量 sat,如下:
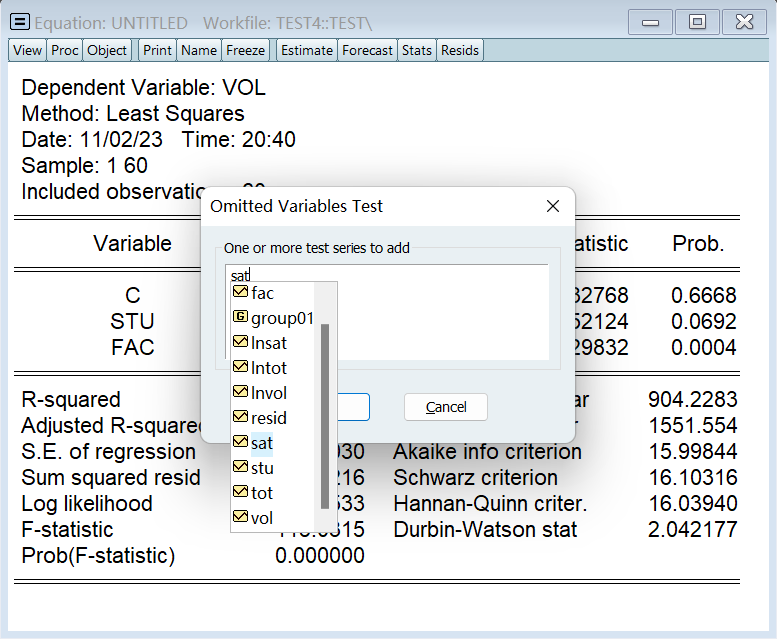
ls vol c stu fac按照下图所示点击相应选项检验是否遗漏变量:
输入 sat,因为我们认为它可能是遗漏的变量:
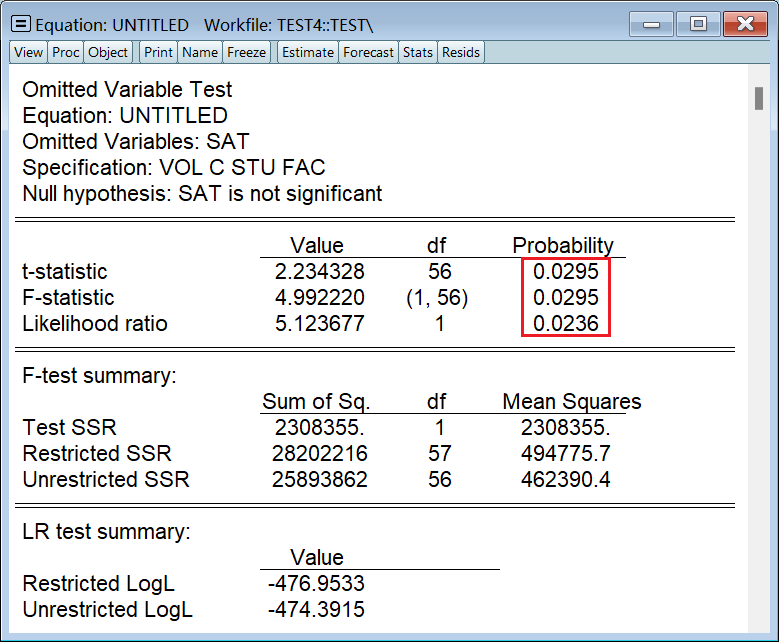
看这三个检验结果即可,它们都一致认为 sat 是遗漏变量:
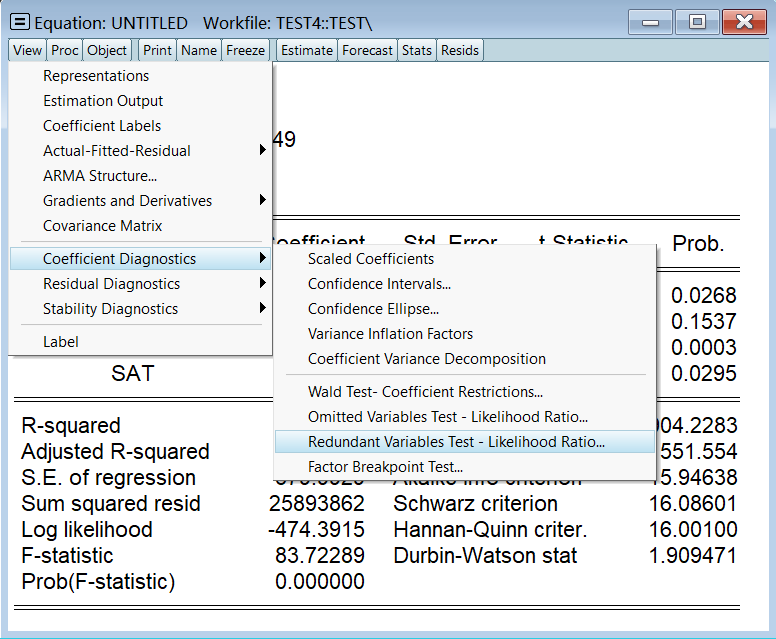
2-1、检验是否加入了不相干变量
当前解释变量为 stu、fac、sat,检验 stu 是否是不相干变量:
看这三个检验结果即可,它们都一致认为 stu 是不相干变量:
2-2、惩罚新增变量
- 赤池信息准则(AIC)
- 施瓦茨信息准则(SC)
用于在新增变量前的模型和新增变量后的模型之间比较,两个的值越低越好:
3、修改函数形式:生成新变量
假设我们需要把原模型变成双对数形式,那么就需要对每个变量取对数。在 EViews 中的实现方式就是生成新的变量,利用新变量重新做一次回归。
- genr 是生成新变量的指令
- lnvol 是新变量的名称
- log() 是函数
- vol 是原变量
genr lnvol=log(vol)
genr lntot=log(tot)
genr lnsat=log(sat)再利用新变量做回归:
ls lnvol c lntot lnsat五、描述性统计分析
1、按组打开
ctrl+鼠标左键,依次点击我们需要的数据,选好后点击右键:
数据在组中的排列顺序=鼠标选择的顺序:
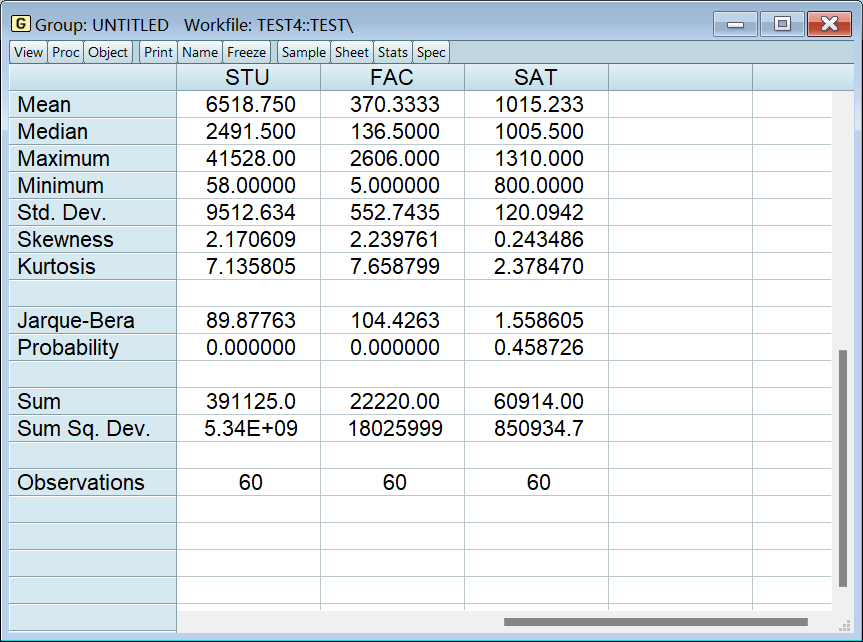
2、查看样本均值
结果如下图所示:
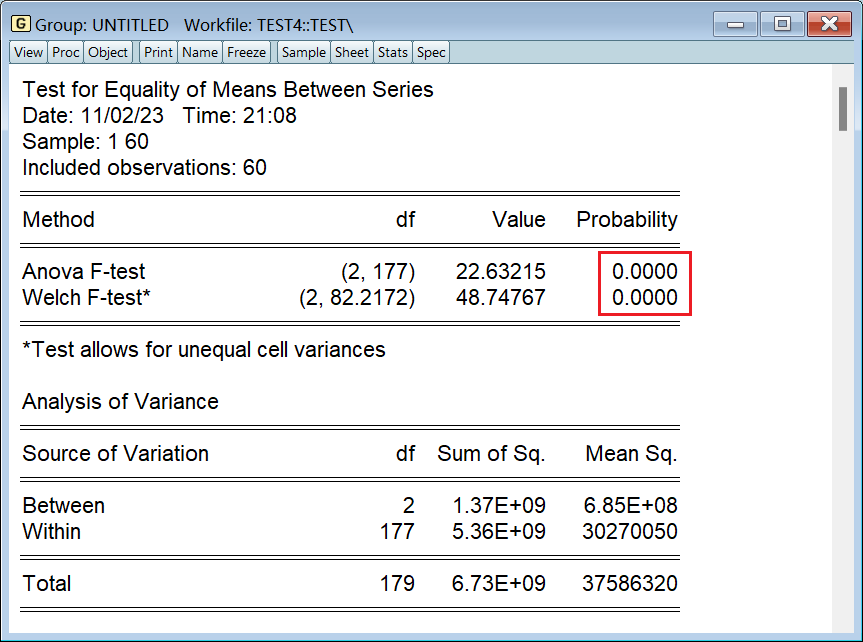
3、样等性检验
检验不同样本的均值是否存在显著差异
选择均值 mean:
看这两个结果即可,表明不同样本的均值没有显著差异:
老师的 EViews 在 F 检验上面还有两种 t 检验,不知道为什么到我这版就没了。
六、多重共线性的检验
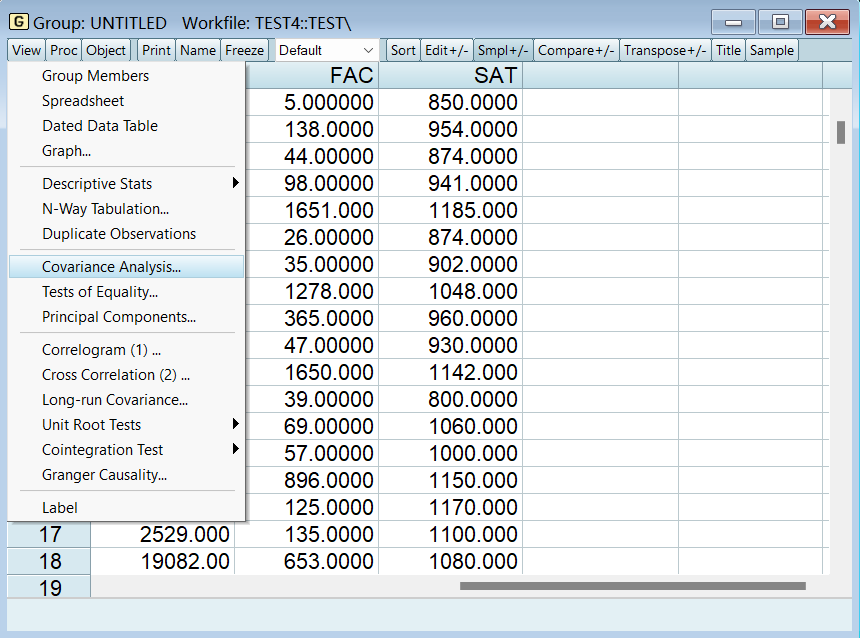
1、相关系数检验
将所需数据按组打开,并选择协方差分析:
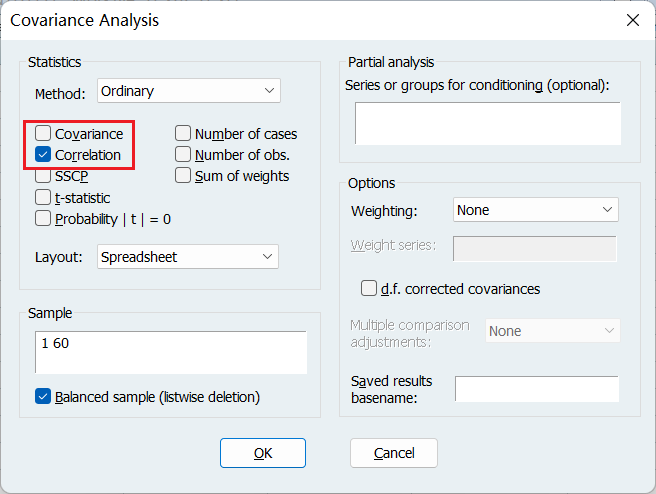
这里改选相关系数,不要选协方差:
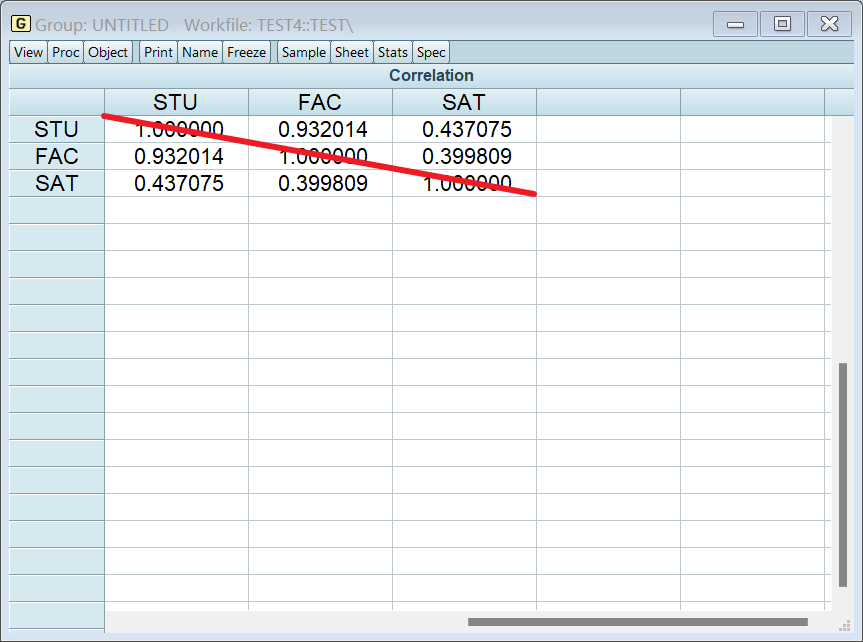
相关系数矩阵都是对称矩阵,所以可以只看主对角线下面的内容:
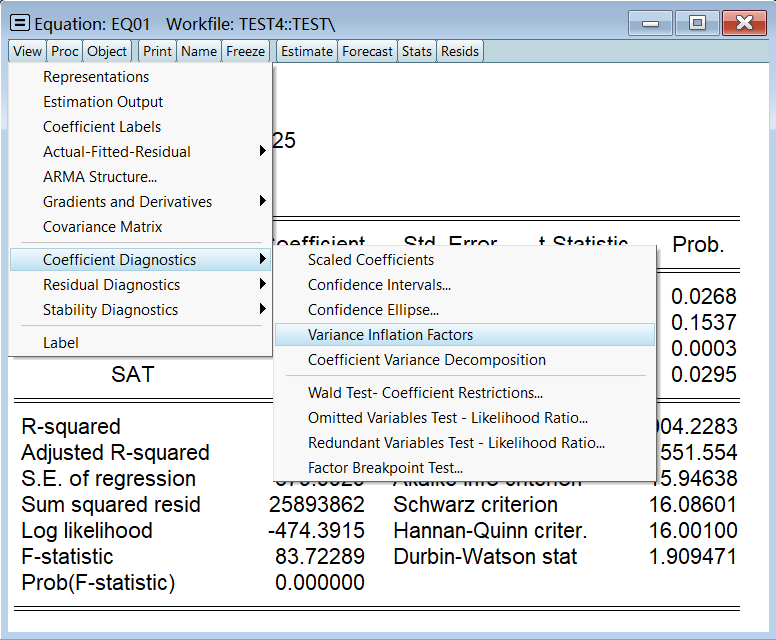
2、VIF 膨胀因子检验
VIF 是在回归方程结果页做的,不是按组打开数据那里:
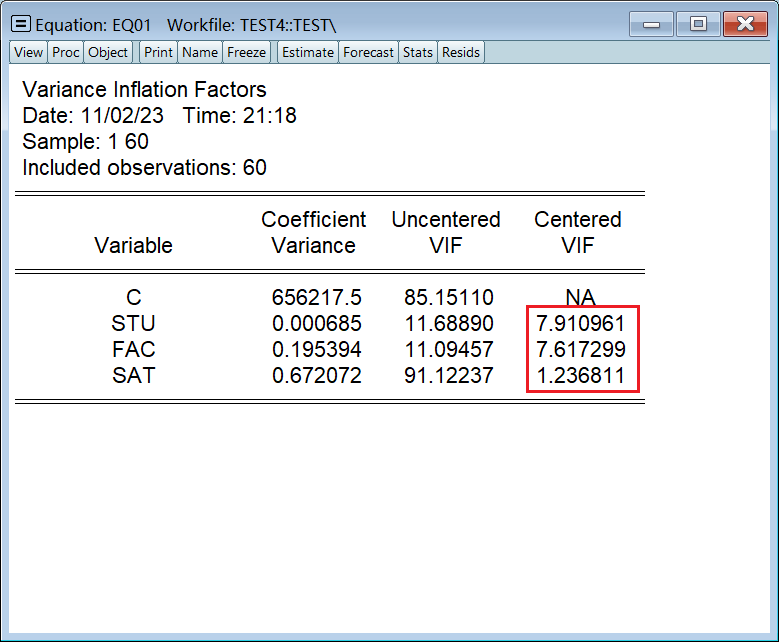
只需要看第三列结果,VIF > 5 就认为存在多重共线性:
这里 STU 和 FAC 的 VIF 都大于 5,只有 SAT 置身事外,所以肯定是 STU 和 FAC 之间存在多重共线性。
七、异方差的检验和补救
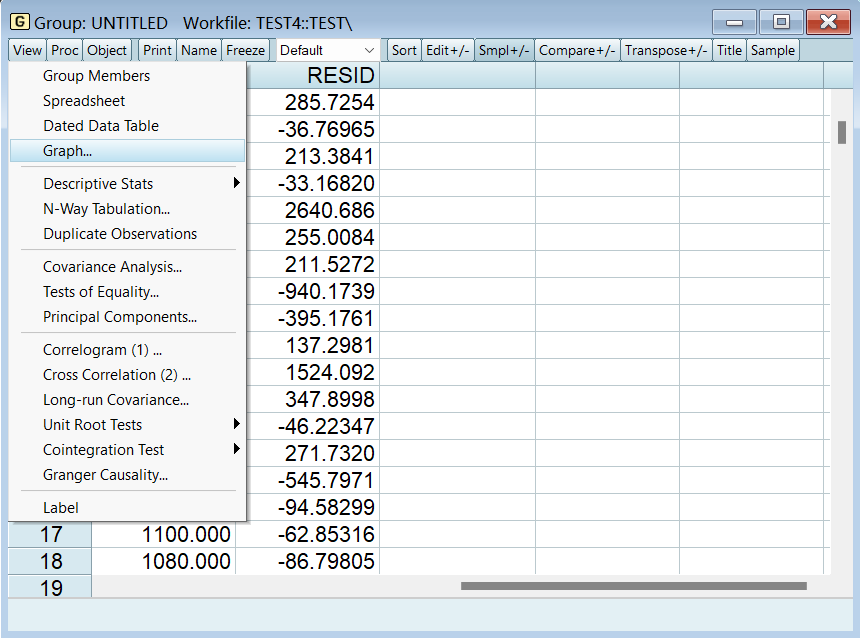
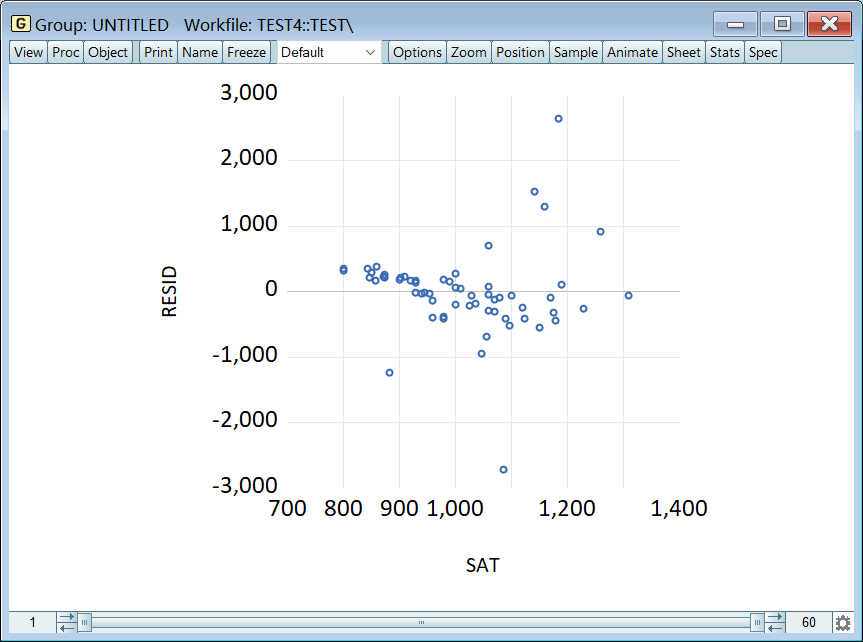
1、图解法(检验)
将一个解释变量和 resid 按组打开,先选解释变量后选 resid,否则 x 和 y 轴颠倒了:
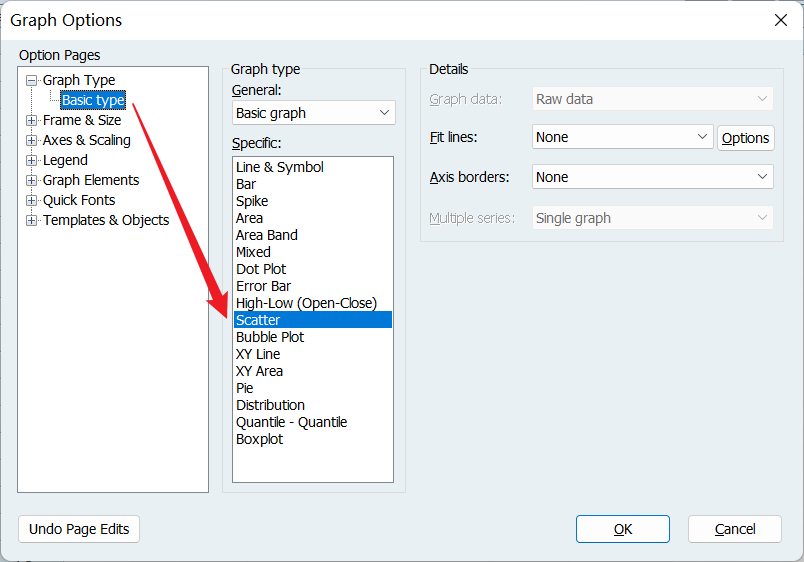
选择散点图:
可以看出残差的分布随 SAT 的增大而增大了,因此可能存在异方差:
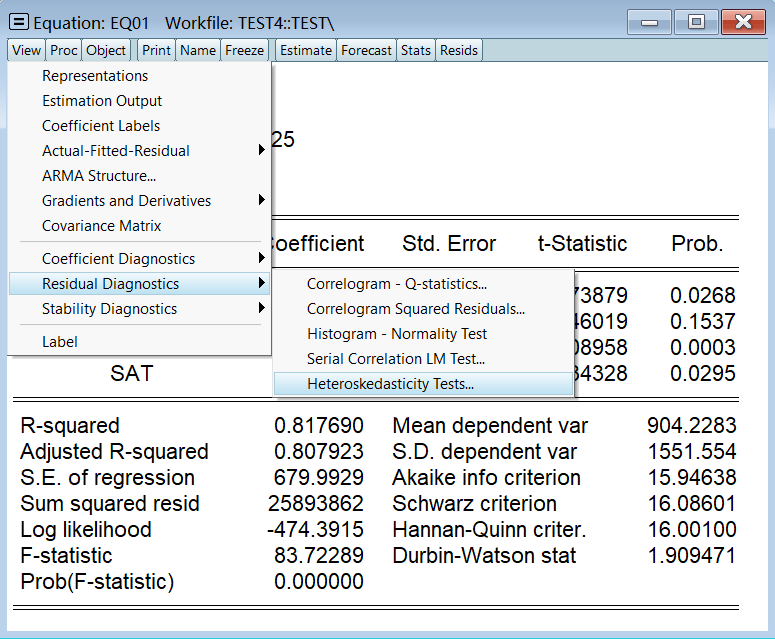
2、White 检验
White 检验是在回归方程结果页做的,不是按组打开数据那里:
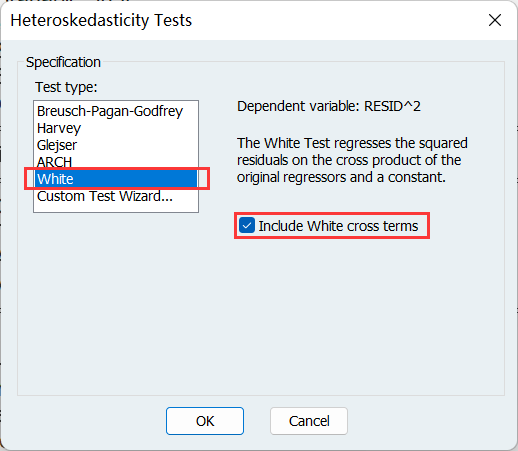
选择 White 检验,勾选框可以选择要不要交叉项:
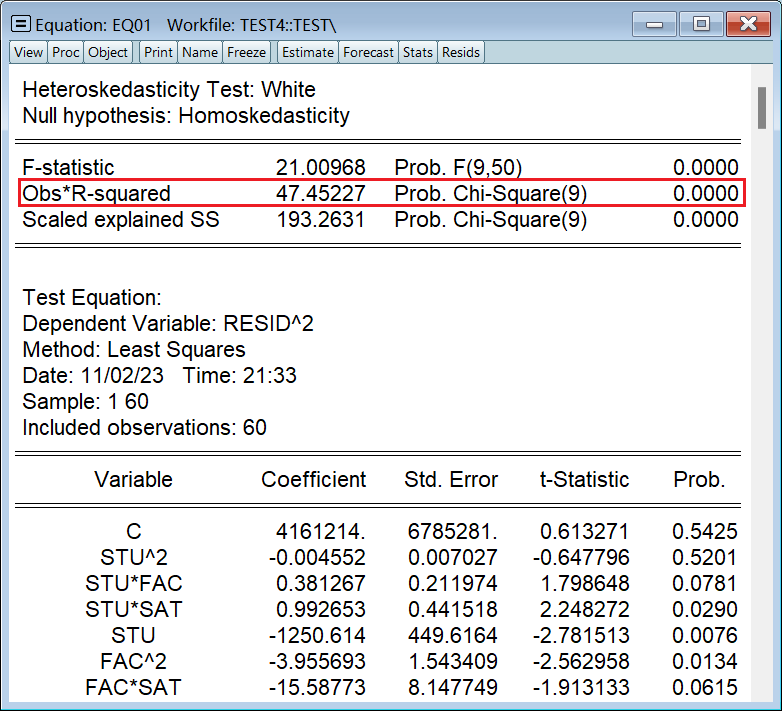
White 检验的统计量是 nR^2,可以看出模型不存在异方差:
所以图解法不靠谱啊……
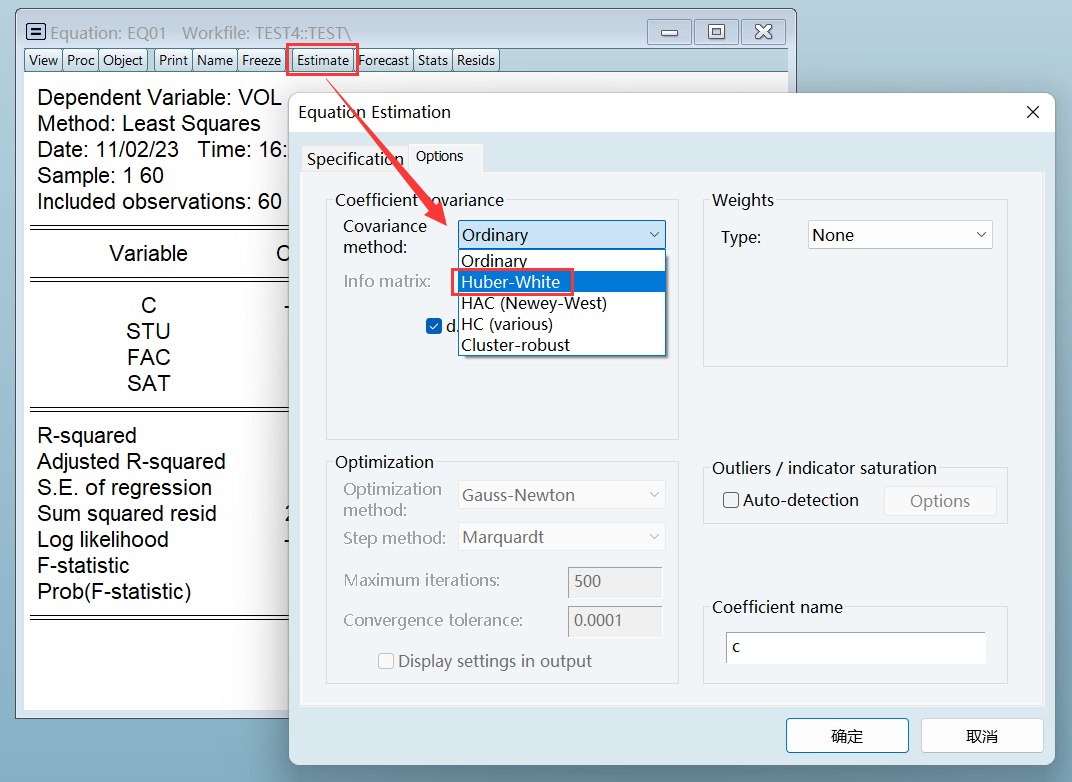
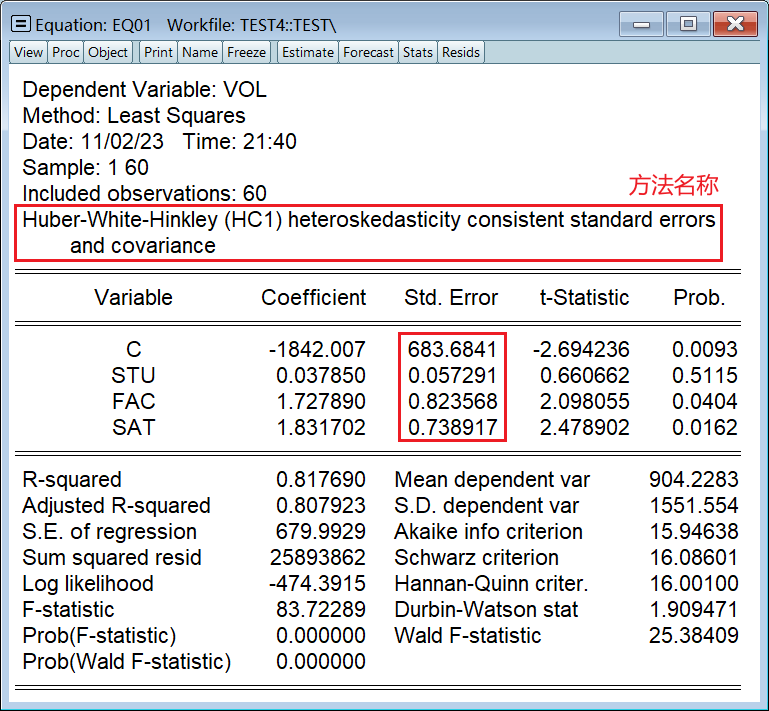
3、White 调整法(补救)
White 调整法只会修正标准差,不会影响到参数估计值:
八、序列相关性的检验和补救
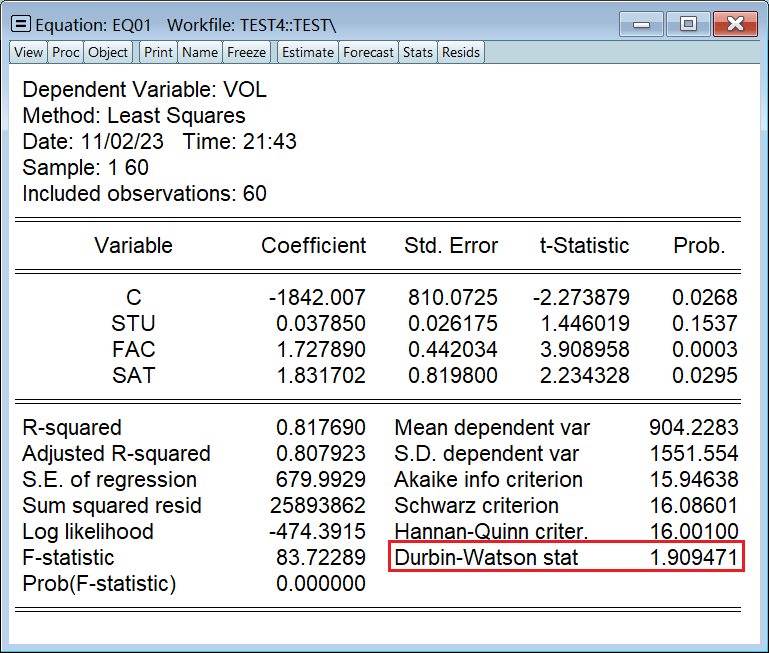
1、DW 值(检验)
DW 统计量值是给你算出来了,但是要自己查表去看到底是不是序列相关:
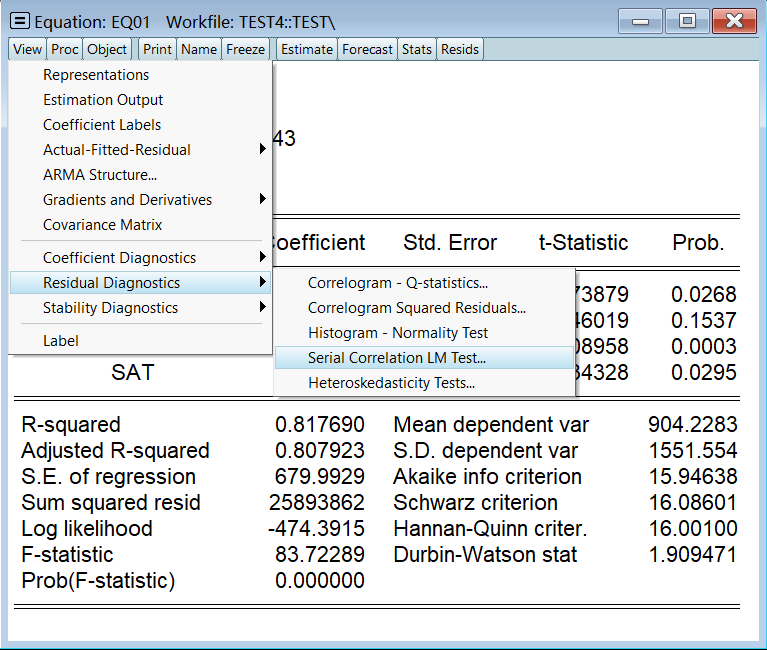
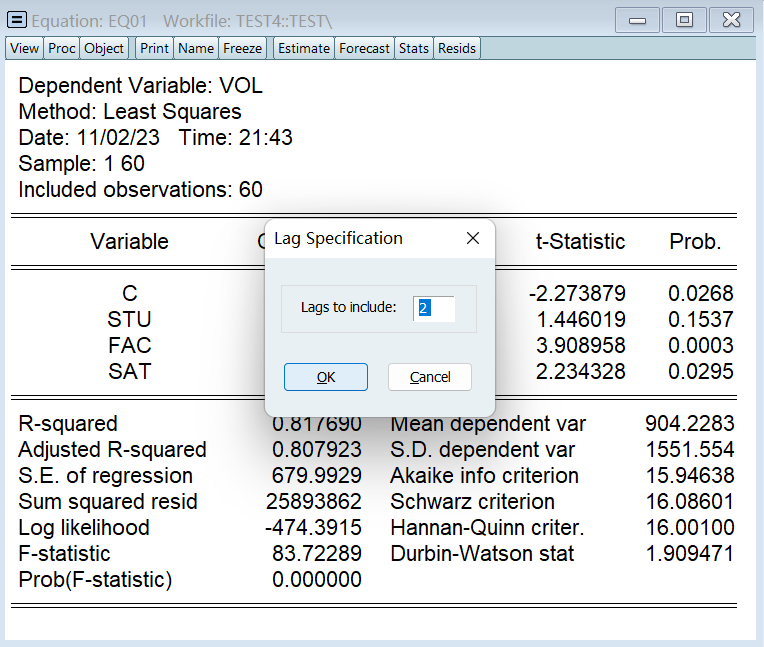
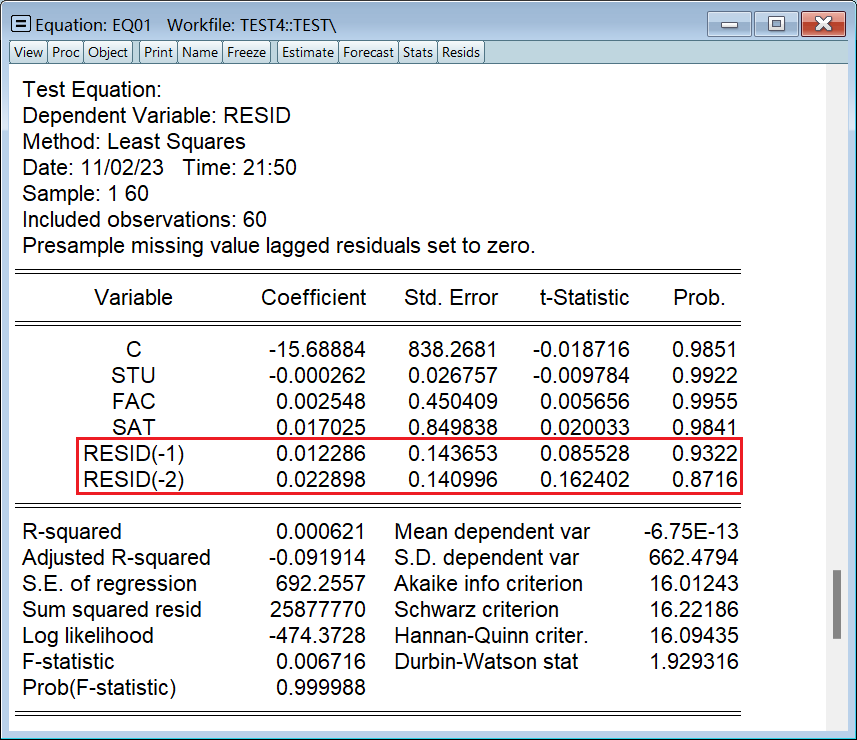
2、LM (BG) 检验
DW 只能检验一阶,我们 LM 至少要检验个二阶:
结果是既没有一阶序列相关性,也没有二阶序列相关性:
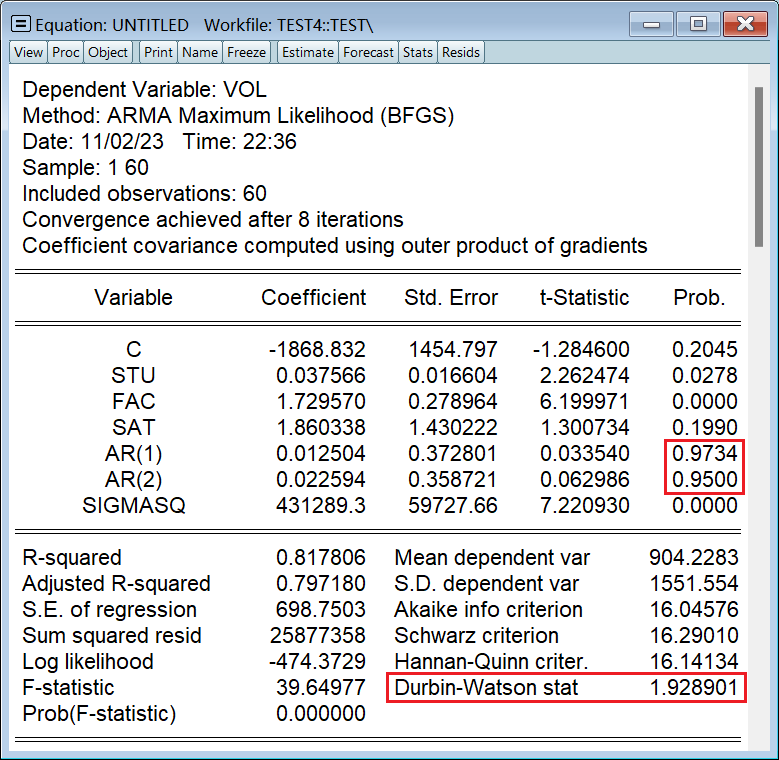
3、GLS 法(补救)
引入解释变量 AR(m),表示随机误差项 ε_t 的 m 阶滞后项 ε_(t-m):
ls vol c stu fac sat ar(1) ar(2)两个滞后项的参数估计值不显著异于 0,因此不存在序列相关性;否则,标准差的值将得到修正,STU、FAC、SAT 的参数估计值也会改变。正因为原模型不存在序列相关性,所以修正前后的参数估计值不变,DW 值几乎也没有变:
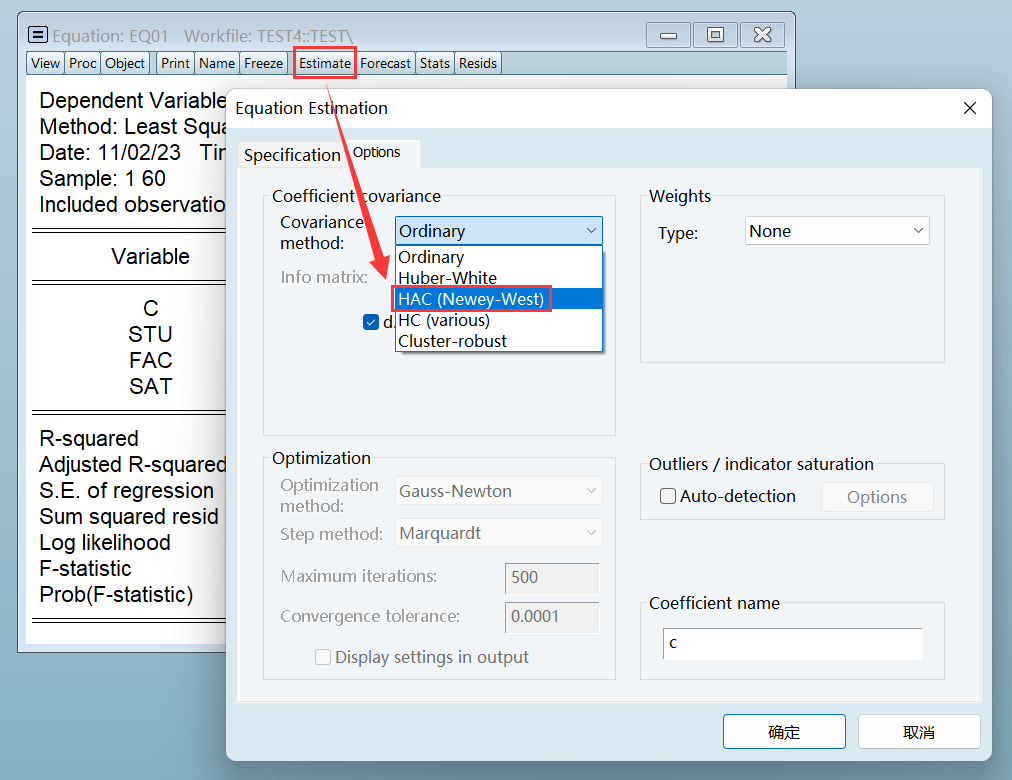
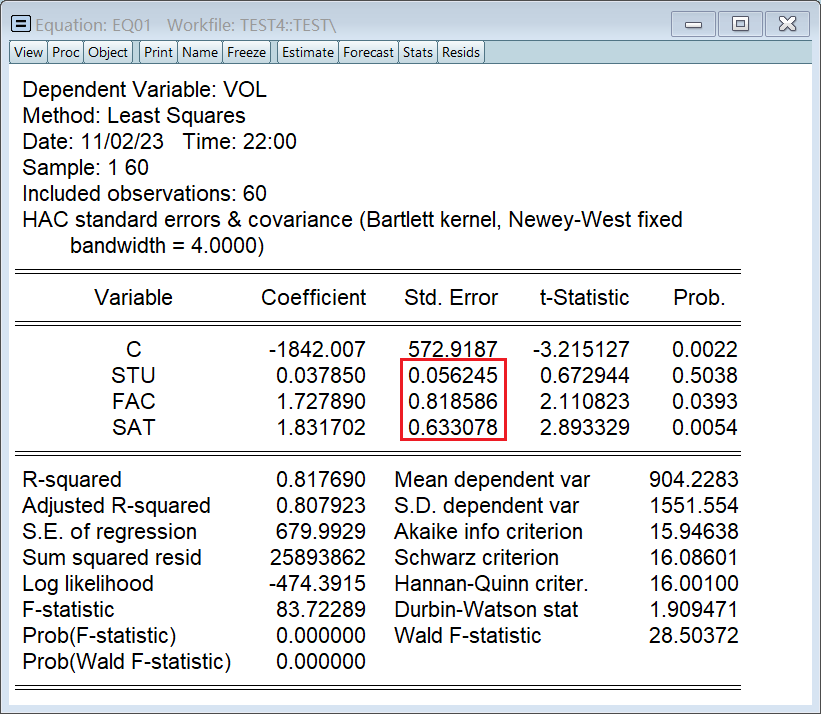
4、Newey-West 法(补救)
NW 调整法只会修正标准差,不会影响到参数估计值:
九、虚拟因变量
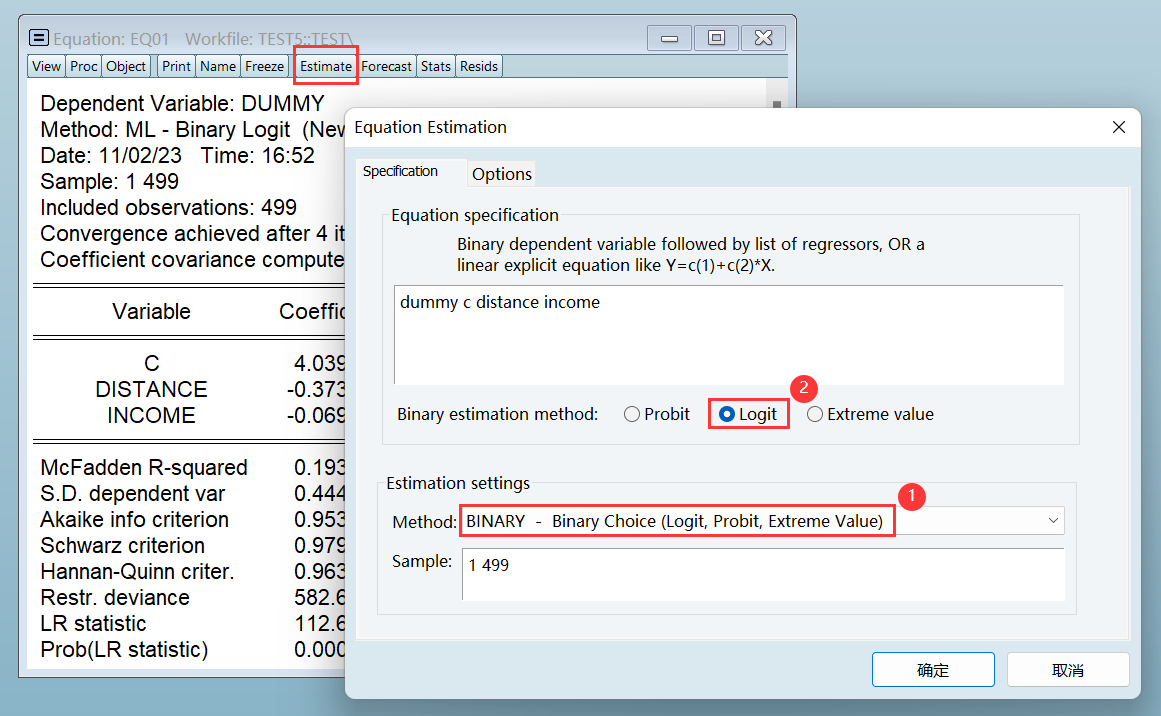
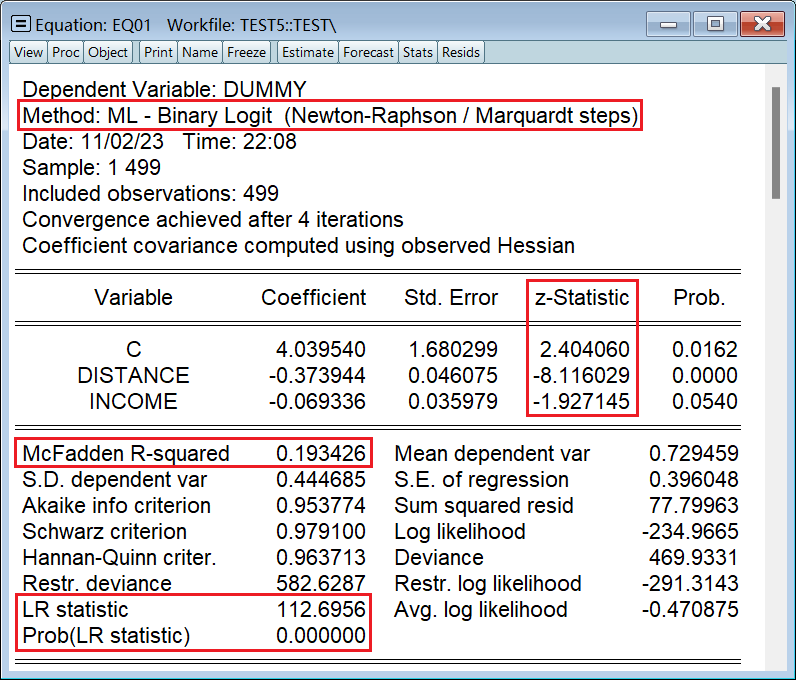
1、Logit 模型
和 OLS 统计检验的三大区别:
- 参数估计值的显著性:t 检验 << z 检验
- 模型的拟合程度:R^2 << R^2_McF
- 模型的总体显著性:F 检验 << LR 检验
2、Probit 模型
类比 Logit 模型,就只是勾选的框框不同。