问题描述

我们可以把由 $0$ 和 $1$ 组成的字符串分为三类：全 $0$ 串称为 $B$ 串，全 $1$ 串称为 $I$ 串，既含 $0$ 又含 $1$ 的串则称为 $F$ 串。

$FBI$ 树是一种二叉树，它的结点类型也包括 $F$ 节点，$B$ 节点和 $I$ 节点三种。由一个长度为 $2^n$ 的 $01$ 串 $S$ 可以构造出一棵 $FBI$ 树 $T$，其构造方法如下：

$T$ 的根节点为 $R$，其类型与串 $S$ 的类型相同；

若串 $S$ 的长度大于 $1$，将串 $S$ 从中间分开，分成等长的左右子串 $S_1$ 和 $S_2$；由左子串 $S_1$ 构造 $R$ 的左子树 $T_1$，由右子串 $S_2$ 构造 $R$ 的右子树 $T_2$。

现在给定一个长度为 $2^N$ 的 $01$ 串，请用上述构造方法构造出一棵 $FBI$ 树，并输出它的后序遍历序列。

输入格式

第一行是一个整数 $N(0\le N\le 10)$。

第二行是一个长度为 $2^N$ 的 $01$ 串。

输出格式

一行，这一行只包含一个字符串，即 $FBI$ 树的后序遍历序列。

样例

样例输入1：

3
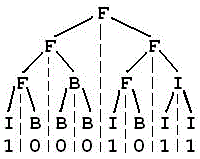
10001011

样例输出1：

IBFBBBFIBFIIIFF

样例1解释：

数据范围

对于 $40\%$ 的数据，$0\le N\le 2$。

对于 $100\%$ 的数据，$0\le N\le 10$。

题解

题目中给出了一个 $01$ 串。

我们考虑如何构造这棵树。首先，长度为 $1$ 的串一定能知道是 I 串还是 B 串。然后，长度为 $2$ 的串可以由两个长度为 $1$ 的串合并得到结果。以此类推，最终能得到整棵树的结果。

合并时，若两个串都为 I 串，则合并的串也是 I 串；若两个串都为 B 串，则合并的串也是 B 串；否则合并的串时 F 串。

接下来只需要按后序遍历输出即可。

int n;
string s;
int dfs(int x, int y){
	if(y == 0){
		if(s[x - (1 << n) + 1] == '0'){
			printf("B");
			return 0;
		}
		printf("I");
		return 1;
	}
	int t = -1;
	int f1 = dfs(2 * x, y - 1);
	int f2 = dfs(2 * x + 1, y - 1);
	//合并，不用像我以前一样写的那么复杂，只需要判断B和I，剩下的情况都是F
	if(f1 == 0){
		if(f2 == 0){
			t = 0;
		}
		else{
			t = 2; 
		} 
	}
	else if(f1 == 1){
		if(f2 == 1){
			t = 1;
		}
		else{
			t = 2;
		}
	}
	else{
		t = 2;
	}
	if(t == 0){
		printf("B");
	}
	else if(t == 1){
		printf("I");
	}
	else if(t == 2){
		printf("F");
	}
	return t;
}
int main(){
	scanf("%d", &n);
	cin >> s;
	s = " " + s;
	dfs(1, n);
	return 0;
}