💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
分布式学习与多智能体系统的协同控制
摘要:
本文提出了一种分布式学习与协同控制算法,并对多智能体系统进行了分析,使得智能体通过局部行为能够实现整个系统的全局目标。我们考虑了一个资源受限的多智能体系统,其中每个智能体在感知、计算和通信方面的能力有限。所提出的算法由每个智能体独立执行,用于从噪声测量中估计未知场,并以分布式方式协调多个智能体以发现未知场的峰值。每个移动智能体维护其对场的本地估计值,并使用自身及其附近智能体的集体测量值更新该估计值。然后,每个智能体利用其估计场的梯度向场的峰值移动,同时避免碰撞并保持通信连接。所提出的算法基于对未知场的递推空间估计。我们证明,所提出的多智能体系统的闭环动态可以转化为随机逼近算法的形式,并利用Ljung的常微分方程(ODE)方法证明了其收敛性。我们还提供了广泛的仿真结果以支持我们的理论结果。
关键词:协同控制;多智能体系统;递推参数估计
1. 引言
近年来,无线传感器网络引起了越来越多的关注(Culler, Estrin, & Srivastava, 2004; Estrin, Culler, Pister, & Sukhatme, 2002)。无线传感器网络由大量传感器节点组成。每个传感器节点能够进行感知和计算,这些节点通过无线网络进行通信,形成一个临时的网络。无线传感器网络的应用包括但不限于环境监测、建筑舒适性控制、交通控制、制造业和工厂自动化以及监控系统(Oh, Schenato, Chen, & Sastry, 2007,以及其中的参考文献)。然而,面对环境的动态性,静态传感器网络有时显得不足,而移动传感技术因其适应性和高分辨率采样能力而展现出优越性能(Singh et al., 2007)。
传感器网络的移动性可以增加其在空间和时间上的感知覆盖范围,并提高对环境动态变化的鲁棒性。与无线传感器网络类似,每个移动智能体的资源是有限的;它们在短通信范围内运行,具有有限的内存和计算能力。这些移动智能体通过无线网络进行通信。尽管每个智能体的能力有限,但作为一个群体,它们可以完成与少数高端移动智能体相当的各种任务。为了执行诸如探索、监视和环境监测等任务,需要对移动传感智能体进行分布式协调,以实现全局目标,这一领域最近受到了广泛关注(Cortes, Martinez, Karatas, & Bullo, 2004; Jadbabie, Lin, & Morse, 2003; Olfati-Saber, 2006; Ren & Beard, 2005; Tanner, Jadbabaie, & Pappas, 2003)。
在移动传感智能体的分布式协调中,一个具有挑战性的问题是未知场的梯度爬升,这一问题吸引了环境科学家和控制工程师的广泛关注(Őgren, Fiorelli, & Leonard, 2004, DOD/ONR MURI)。这是由于在分布式环境中跟踪毒素的众多应用。一个有趣的实际应用是在湖泊中追踪有害藻华。在某些环境条件下,湖泊和海洋中快速繁殖的有害藻华会产生蓝藻毒素(大湖区卓越中心)。接触含有藻类蓝藻毒素的水会对人类健康造成严重的急性或慢性影响,并对水生生物产生不利影响(大湖区卓越中心;有害藻华观测系统)。叶绿素水平与藻类和蓝藻生物量密切相关。因此,人们一直在努力在关注的区域生成叶绿素的估计场(图1)。基于上述动机,我们的目标是为多智能体系统开发理论健全的控制算法,以追踪感兴趣的标量场的峰值(例如,有害藻华、温度、pH值、盐度、毒素和化学羽流等)。一般来说,这些标量参数提供了关于环境质量的丰富信息,例如空气、湖泊和公共水系统。
解决这一追踪问题的最常见方法是受生物启发的趋化作用(Adler, 1966; Dhariwal, Sukhatme, & Requicha, 2004),在这种方法中,移动传感智能体根据感兴趣场的局部梯度进行驱动。然而,这种方法的收敛速度可能较慢,且移动机器人可能会陷入场的局部最大值。在DOD/ONR MURI和Őgren等人(2004)的研究中,提出了在分布式环境中进行自适应梯度爬升的智能体合作网络。集中式网络可以根据感知到的环境调整其配置,以优化其梯度爬升。
梯度爬升问题在生物物种中经常出现。水生生物会寻找富含资源的有利区域,以维持其生存。例如,众所周知,鱼群会沿着营养物质的梯度爬升,以找到最丰富的食物来源。为了寻找资源,鱼群使用“趋性”行为,即它们根据局部梯度在不确定的环境中导航栖息地。Grünbaum(1998)表明,群体行为可以提高执行趋性以爬升梯度的能力,因为群体的对齐倾向可以平均化个体的随机采样误差。
Olfati-Saber(2006)和Tanner等人(2003)对Reynolds(1987)的群体算法进行了全面分析。这种群体算法最初是为了在计算机图形学中模拟鸟类群体的运动而开发的,其中每只人工鸟遵循一组相对简单的分布式规则(Reynolds, 1987)。群体中的鸟会协调其邻居的运动,尽量靠近邻居,同时避免碰撞。一般来说,鸟类/鱼类/蚂蚁/蜜蜂的集体群体行为被认为是自然优化的结果(Bonabeau, Dorigo, & Theraulaz, 1999; Eberhart, Shi, & Kennedy, 2001)。
移动传感器网络的空间估计技术的最新进展如下。Martinez(即将出版)描述了一种用于移动传感器网络的分布式插值方案,用于场估计。该方案使用分布式非参数推理方法,并与覆盖控制兼容(例如,Cortes等人,2004)。Cortés(即将出版)描述了一种用于机器人传感器网络的分布式克里金卡尔曼滤波器,以估计感兴趣的场。在这种克里金卡尔曼滤波器的每次迭代中,智能体会根据新测量值执行基于共识的算法(例如,Olfati-Saber和Shamma, 2005),以计算感兴趣变量的平均值。然后执行迭代加权最小二乘算法,以计算场的状态估计值。
在本文中,我们通过扩展群体算法的最新进展(Olfati-Saber, 2006; Tanner等人,2003),为多智能体系统开发了新颖的分布式学习和协同控制算法。学习和控制算法仅使用局部信息在每个智能体上执行,但它们的设计使得智能体作为一个整体表现出集体智能,即智能体群体实现全局目标。在资源受限的多智能体系统中,每个智能体的通信范围与监视区域的大小相比是有限的。因此,智能体无法执行Cortes等人(2004)、Graham和Cortés(2009)以及Martinez(即将出版)中的覆盖控制。相反,每个智能体会进行测量,并从其通信范围内的邻近智能体接收测量值。在接收到集体测量值后,每个智能体会递归更新其对未知静态场的估计值。递归估计基于径向基函数网络,以表示广泛的物理现象。为了找到场的最大值,传感智能体会沿着其自身估计场的梯度爬升。在我们提出的方法中,每个智能体根据自身及其邻居的集体测量值进行递归场估计,而无需克里金卡尔曼滤波器的共识步骤(Cortés,即将出版)。
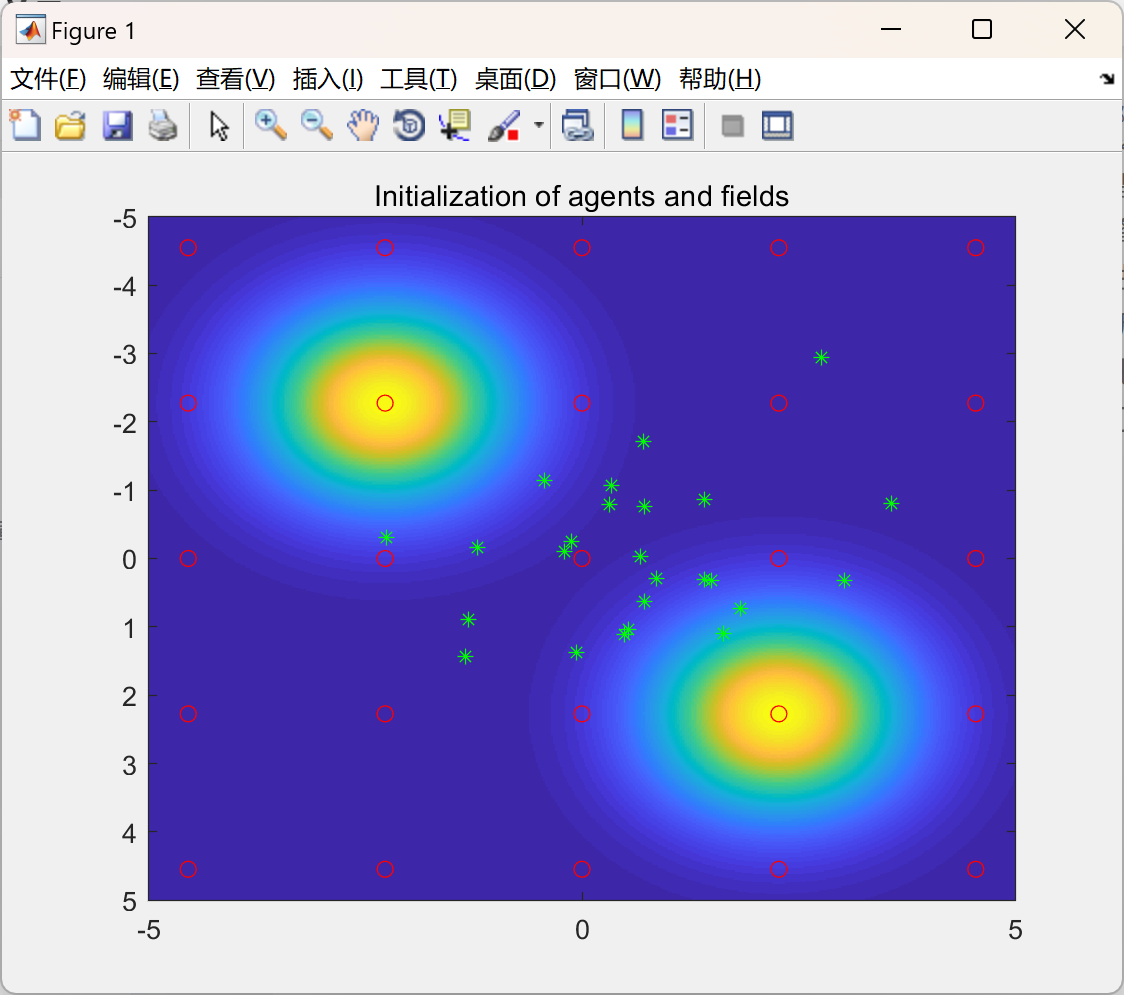
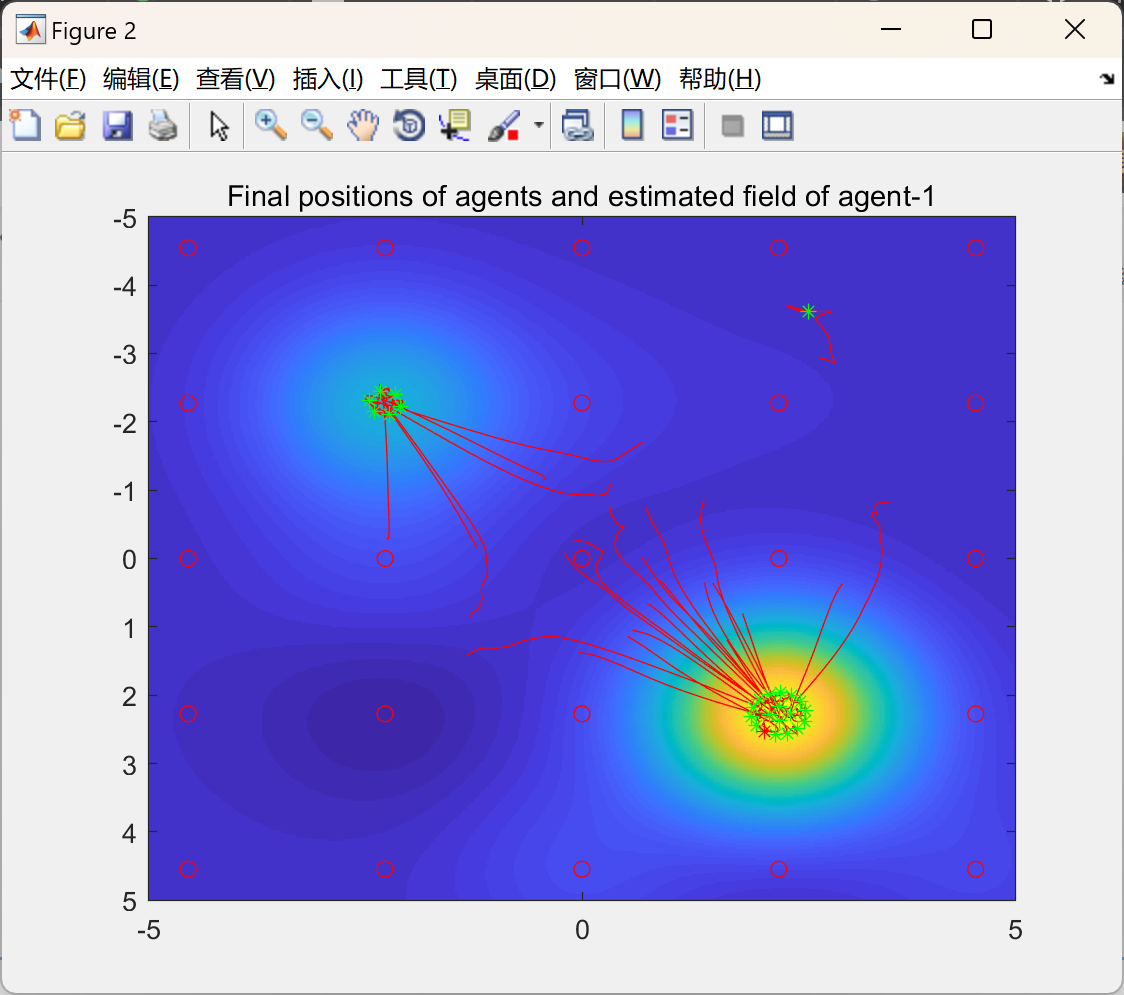
我们提出的协同控制模仿了在不确定环境中局部通信以寻找最丰富资源的动物群体的个体和社会行为。鱼群高效爬升营养物质梯度以寻找食物资源的能力以及生物生物体卓越的地理绘图能力,激发了我们开发多智能体系统的灵感。第5节的仿真结果有力地支持了我们的想法,并验证了与没有协同控制的场估计智能体相比,具有协同控制的多智能体系统的有效性。如图2所示,所提出的多智能体系统能够快速集体定位未知场的最大值,而如果没有通信和群体努力,只有靠近最大值点的少数智能体能够缓慢估计并爬升场的梯度。
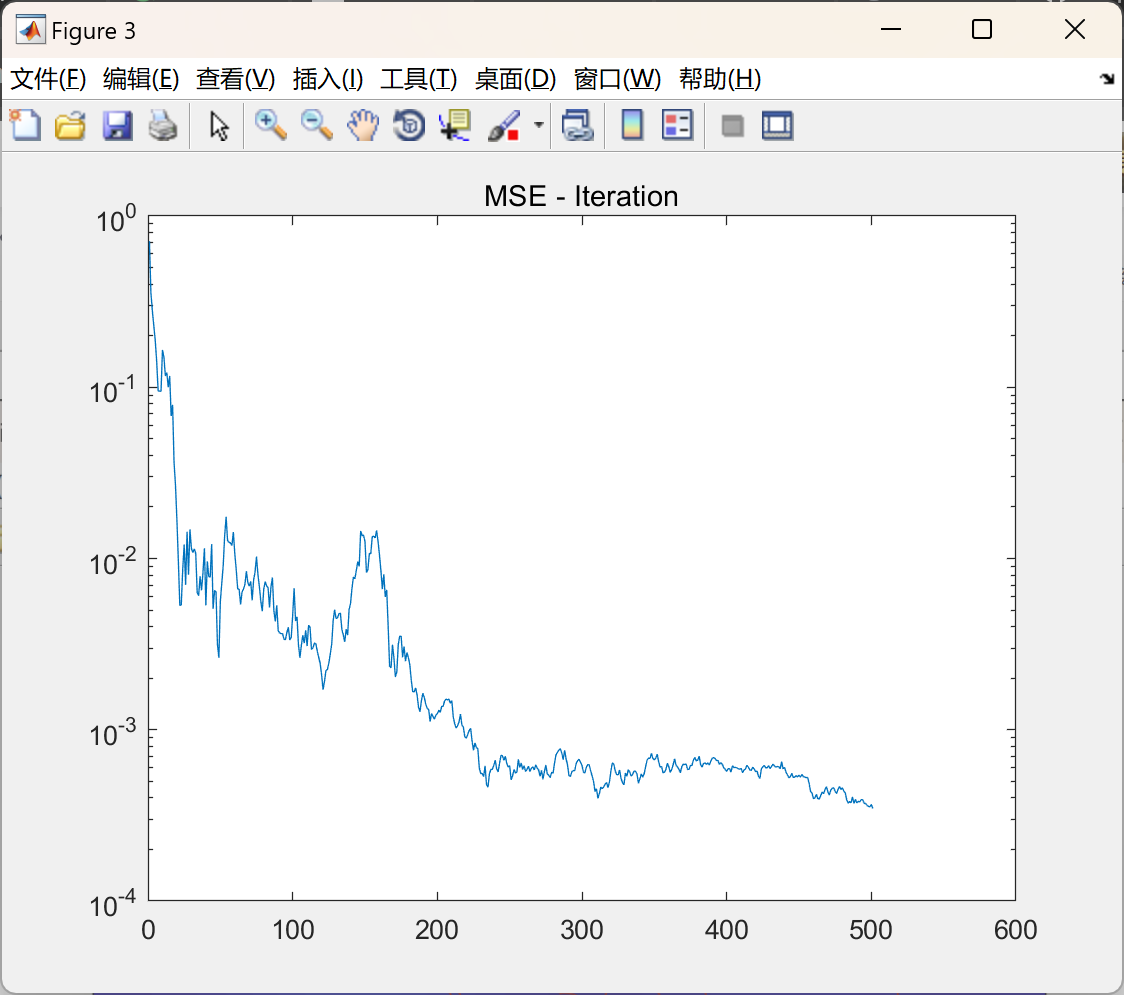
本文还通过将多智能体系统的闭环动态转化为随机逼近算法的形式,提出了所提出的分布式学习和协同控制算法的收敛性质。我们的理论结果基于常微分方程(ODE)方法(Kushner & Yin, 1997; Ljung, 1977)。我们还提出了一组充分条件,以确保算法以概率1收敛。
本文的结构如下。在第2节中,我们简要介绍移动传感网络模型、与图相关的符号以及用于形成群体行为的人工势函数。第3.1节介绍了一种递推径向基函数学习算法,用于映射感兴趣的场。第3.2节描述了基于随机逼近增益的协同学习控制。第4节基于ODE方法分析了所提出的协调算法的收敛性质。第5节通过仿真结果展示了所提出的多智能体系统的有效性,仿真涉及不同的感兴趣场和条件。
6. 结论
本文提出了一类新型的自组织传感智能体,这些智能体形成群体,并通过从邻近智能体处集体获取带噪声的测量值来估计一个未知场,从而实现梯度爬升。所提出的协同学习控制包括基于对未知场的递推估计的运动协调,该估计考虑了测量噪声。我们的协同学习控制策略可以应用于移动智能体的一类广泛的协调算法,适用于在未知场需要被估计的场景中。我们证明,所提出的多智能体系统的闭环动态可以转化为随机逼近算法的形式。因此,我们利用常微分方程(ODE)方法分析了所提出的多智能体系统的收敛性质,并通过针对不同参数和条件的仿真研究进行了验证。对于所提出的多智能体系统和没有通信及群体努力的学习智能体的仿真结果清楚地展示了通信网络和群体努力的优势。受本文开发的技术的启发,我们目前正在开发一种系统化的方法,以便高效设计和分析一类适用于多智能体系统分布式学习和控制的实际算法。未来可能的研究方向是探讨如何通过共识类算法最优地协调异构学习智能体的混合群体,以学习未知场。
详细文章见底第4部分下载。
📚2 运行结果
部分代码:
%% Generate the Scalar Field
m=25; % The number of radial basis function used to generate the field is m
reg_x=[-5,5]; % These are x and y limite for the region
reg_y=[-5,5];
% Kernels=[(reg_x(2)-reg_x(1))*rand(m,1)+reg_x(1) (reg_y(2)-reg_y(1))*rand(m,1)+reg_y(1)]; % This contains the positions of the RBFs
Kernels=[kron(linspace(reg_x(1),reg_x(2),5)/1.1,[1 1 1 1 1])',repmat(linspace(reg_y(1),reg_y(2),5)/1.1,1,5)'];
% Gamma=0.1*abs(randn(m,1)); % Gamma in the RBFs
Gamma=0.1*ones(m,1);
% sigma=2*abs(randn(m,1)); % sigma in the RBFs
sigma=1*ones(m,1);
% Theta=0.1*abs(randn(m,1)); % scaling factors of RBFs
Theta=zeros(m,1);
Theta(19)=5; % This set a peak for the field
Theta(7)=5;
% This returns the true scalar value of the whole field
mesh_value = generate_region(reg_x,reg_y,m,Gamma,sigma,Kernels,Theta);
M=size(mesh_value,1);
[mesh_x,mesh_y]=meshgrid(linspace(reg_x(1),reg_x(2),M),flip(linspace(reg_y(1),reg_y(2),M)));
image(linspace(reg_x(1),reg_x(2),M),linspace(reg_y(2),reg_y(1),M),mesh_value,'CDataMapping','scaled');
%
title("Initialization of agents and fields")
% view(2);
% plot3(mesh_x,mesh_y,255.*mesh_value./max(max(mesh_value)))
% hold on;
% surf(mesh_x,mesh_y,mesh_value,'edgecolor', 'none');
% hold off;
%% Global parameters definition
N=25; % Number of agents
d=0.6; % a parameter
d0=1.5*d; % a parameter
d1=3.5*d; % a parameter
r=4*d; % The communication range of an agent
s=1; % Sampling rate of agents
sigma_w=1; % variance of the sampling noise
%% Agents initialization
t=0;
InitialPosi=randn(N,2); % Initialize the agent positions
InitialPosi(InitialPosi>5)=4; % correct positions outside the border🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
🌈4 Matlab代码实现、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取