1 KMP概述 —— 什么是KMP

KMP算法是一种高效的字符串匹配算法，由Knuth、Morris和Pratt三位计算机科学家于1977年提出。KMP算法通过在匹配过程中利用已部分匹配的信息来避免不必要的字符比较，从而显著提高了字符串匹配的效率。

2 为什么引入KMP算法？

传统的朴素字符匹配算法过于低效，其效率低得难以忍受。对于字符串𝑆和模式串𝑃来说，最坏情况下的时间复杂度达到 𝑂(𝑛×𝑚)。因此，我们需要引入一种更加高效的字符匹配算法，这就是KMP算法。
首先，我们需要先了解传统朴素算法的模式。

2.1 传统朴素算法

2 为什么引入KMP算法？

传统的朴素字符匹配算法过于低效，其效率低得难以忍受。对于字符串 $S$和模式串$P$来说，最坏情况下的时间复杂度达到$O(n\times m)$。因此，我们需要引入一种更加高效的字符匹配算法，这就是KMP算法。

首先，我们需要先了解传统朴素算法的模式。

2.1 传统朴素算法

2.1 传统朴素算法

传统的朴素字符串匹配算法（也称为暴力算法）是一种直接而简单的字符串匹配方法。其基本思想是从主串 $S$ 的每一个位置开始，逐一尝试匹配模式串 $P$，直到找到匹配或者遍历完整个主串。算法的步骤如下：

1. 初始化：设主串 $S$ 的长度为 $n$，模式串 $P$ 的长度为 $m$。
2. 遍历主串：从主串 $S$ 的每一个位置 $i$（$0\le i\le n-m$）开始，进行如下匹配操作：
   1. 逐字符匹配：从位置 $i$ 开始，将主串 $S$ 的子串 $S[i\cdots i+m-1]$ 与模式串 $P$ 逐字符比较。
   2. 匹配成功：如果在位置 $i$ 开始的 $m$ 个字符与模式串 $P$ 完全匹配，则找到匹配，匹配过程结束。
   3. 匹配失败：如果在位置 $i$ 开始的 $m$ 个字符与模式串 $P$ 存在不匹配字符，则从主串的下一个位置 $i+1$ 重新开始匹配。

朴素算法示例

假设主串 $S$ 为 “ABC ABCDAB ABCDABCDABDE”，模式串 $P$ 为 “ABCDABD”，我们可以使用朴素算法进行匹配：

1. 从 $S$ 的第一个字符开始，比较 “ABC ABCDAB ABCDABCDABDE” 和 “ABCDABD”。
2. 第一轮匹配失败，从主串的第二个字符开始重新匹配。
3. 重复上述过程，直到第8个字符 “ABCDABD” 匹配成功，或者遍历完整个主串。

在朴素算法中，最坏情况下，主串的每一个字符都需要与模式串进行比较，当匹配失败时，需要回退并从下一个字符重新开始匹配。因此，总的比较次数在最坏情况下为nm。

为了提高字符串匹配的效率，需要引入更高效的算法。KMP算法正是为了克服朴素算法的低效性而提出的。KMP算法通过利用部分匹配表（前缀函数）来避免不必要的字符比较，从而显著降低了匹配过程中的时间复杂度，使其在最坏情况下的时间复杂度降为 $O(n+m)$。这使得KMP算法在处理大规模字符串匹配问题时，具有显著的性能优势。

3 KMP核心思想

3 KMP核心思想

3.1 核心思想

KMP算法的核心思想是最大程度地利用已知信息，避免重复执行已有操作。在传统的朴素字符串匹配算法中，当匹配失败时，需要从头重新开始匹配。KMP算法通过预处理模式串，建立一个部分匹配表，（即根据子串生成一个next数组），在匹配过程中利用这个表来避免重复的比较操作，从而提高匹配效率。

3.2 优化朴素算法的切入点

在朴素算法中，当主串和模式串匹配失败时，主串的指针𝑖会回退，导致重复比较。KMP算法的优化思路是利用模式串本身的结构信息，避免不必要的回溯和重复比较。
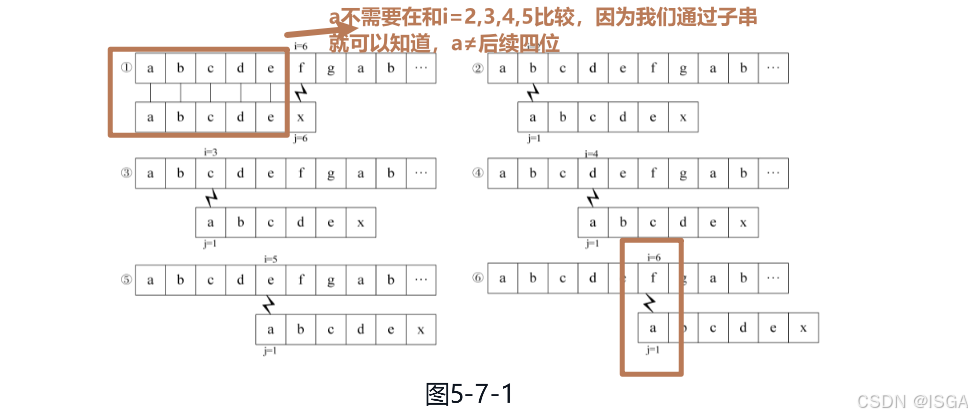
由下图可以知道，2、3、4、5中，指针i实际上在不断的回退进行重复比较，这些步骤可以直接跳过，我们实际上可以仅执行步骤6。

关键点

KMP算法的关键在于部分匹配表（前缀函数）的构建。这个表记录了模式串中每个位置的前缀和后缀的最长相等长度，从而在匹配失败时，可以根据这个表来确定模式串的指针跳转位置。具体来说，这个跳转位置由模式串的结构决定，而与主串无关。如下图，可以直观的看到，j指针的值的变化，只是与其子串本身相关，关键就取决于T串的结构中是否有重复的问题。

示例

假设模式串 $P="ABCDABD"$，其next数组构建过程如下：

1. 初始化 next[0] = 0，j = 0。
2. 从 $i=2$ 开始遍历：
   • $i=2$：P[2] != P[0]，next[2] = 0。
   • $i=3$：P[3] != P[0]，next[3] = 0。
   • $i=4$：P[4] != P[0]，next[4] = 0。
   • $i=5$：P[5] == P[1]，j = 1，next[5] = 1。
   • $i=6$：P[6] == P[2]，j = 2，next[6] = 2。
   • $i=7$：P[7] != P[3]，j = \text{next}[1] = 0，next[7] = 0。

最终构建的 next 数组为 [0, 0, 0, 0, 1, 2, 0]。

通过理解和构建 next 数组，KMP 算法可以在匹配过程中利用部分匹配信息，避免重复比较，从而实现高效的字符串匹配。

4 KMP核心部分

4.1 KMP匹配过程

KMP算法的匹配过程通过使用部分匹配表（即next数组）来避免重复比较，从而提高匹配效率。具体的匹配过程如下：

1. 初始化：

   • 定义主串 $S$ 的长度为 $n$，模式串 $P$ 的长度为 $m$。
   • 预处理模式串 $P$，构建next数组。

2. 匹配过程：

   • 设主串的当前匹配位置为 $i=1$，模式串的当前匹配位置为 $j=0$（注意：这里的索引从1开始）。
   • 当 $i\le m$ 时，进行如下操作：
     1. 如果 $S[i]==P[j+1]$，则 $i$ 和 $j$ 同时加1，即匹配成功一个字符，继续匹配下一个字符。
     2. 如果 $S[i]\ne P[j+1]$ 且 $j>0$，则根据next数组，更新 $j$ 的值为 $\text{next}[j]$，不移动 $i$。
     3. 如果 $S[i]\ne P[j+1]$ 且 $j==0$，则仅移动 $i$ 加1，继续从主串的下一个字符开始匹配。

3. 匹配结束：

   • 当 $j==n$ 时，表示模式串 $P$ 完全匹配主串 $S$ 的一部分，此时匹配成功。
   • 如果遍历完整个主串 $S$ 后，未找到完全匹配的部分，则匹配失败。

匹配过程代码：

// kmp 匹配
for(int i = 1, j = 0; i <= m; i++) {
    while(j && s[i] != p[j+1]) j = ne[j];
    if(s[i] == p[j+1]) j++;
    if(j == n) { // j==n，代表匹配出了一个完整的模式串
        // 匹配成功
        // ...匹配成功后的行为
        j = ne[j]; // j回退，下一轮匹配
    }
}

4.2 next数组

定义

我们把模式串 $P$ 中各个位置的 $j$ 值的变化定义为一个数组 next。顾名思义，next数组表示 $j$ 值的下一跳（下一步回退到哪儿）的值。

对于长度为 $j$，从1开始计数的字符串而言，第 $k$ 个位置是从头数第 $k$ 个字符，第 $j-k$ 是从结尾数第 $k$ 个字符。所以 $k$ 与 $j-k$ 是在字符串上相对称的两个位置。

$$\text{next}[i]\text{ 表示，以位置 }i\text{ 为终点的模式串的前缀和后缀相等的最长长度。}$$

求next数组的过程

构建next数组的步骤如下：

1. 初始化：

   • 设模式串 $P$ 的长度为 $n$。
   • 初始化 next 数组，设 next[0] = 0。
   • 设变量 $j=0$，用于记录最长前缀和后缀相等的长度。

2. 构建过程：

   • 从模式串的第二个字符开始，遍历模式串，设当前字符位置为 $i$。
   • 当 $i\le n$ 时，进行如下操作：
     1. 如果 $P[i]==P[j+1]$，则 $j$ 加1，next[i] = j，$i$ 加1。
     2. 如果 $P[i]\ne P[j+1]$ 且 $j>0$，则根据next数组，更新 $j$ 的值为 $\text{next}[j]$，不移动 $i$。
     3. 如果 $P[i]\ne P[j+1]$ 且 $j==0$，则 next[i] = 0，$i$ 加1。

求next数组过程的代码：

// 计算next数组
for(int i = 2, j = 0; i <= n; i++) {
    while(j && p[i] != p[j+1]) j = ne[j];
    if(p[i] == p[j+1]) j++;
    ne[i] = j;
}

示例

假设模式串 $P="ABCDABD"$，其next数组构建过程如下：

1. 初始化 next[0] = 0，j = 0。
2. 从 $i=2$ 开始遍历：
   • $i=2：P[2]!=P[0]，next[2]=0$。
   • $i=3：P[3]!=P[0]，next[3]=0$。
   • $i=4：P[4]!=P[0]，next[4]=0$。
   • $i=5：P[5]==P[1]，j=1，next[5]=1$。
   • $i = 6：P[6] == P[2]，j = 2，next[6] = 2。
   • $i=7：P[7]!=P[3]，j=\text{next}[1]=0，next[7]=0$。

最终构建的 next 数组为 [0, 0, 0, 0, 1, 2, 0]。

5 参考例题

此例题来自AcWing，是一道模板题，可供熟悉KMP模板，熟悉KMP核心部分即可完成此题。
题目信息：

完整代码：

#include <iostream>

using namespace std;

const int N = 100010, M = 1000010;

char s[M], p[N];
int n, m;
int ne[N];

int main()
{
    cin >> n >> (p + 1) >> m >> (s + 1);

    // init next[]
    for (int i = 2, j = 0; i <= n; i++)
    {
        while (j && p[i] != p[j + 1])
        {
            j = ne[j];
        }
        if (p[i] == p[j + 1])
            j++;
        ne[i] = j;
    }

    // kmp
    for (int i = 1, j = 0; i <= m; i++)
    {
        while (j && s[i] != p[j + 1])
        {
            j = ne[j];
        }
        if (s[i] == p[j + 1])
            j++;
        if (j == n)
        {
            printf("%d ",i-n);
            j = ne[j];
        }
    }

    return 0;
}

[1]: 《大话数据结构》
[2]: AcWing 算法基础课