经典问题：

长度为 n 的整数序列 a₁​ … a_n ，输出每个元素左(右)侧首个大(小于)于其的元素下标；没有则输出 0。

朴素做法:

需要对每个元素左(右)侧元素进行遍历，时间复杂度为O(n²) 。

单调栈做法：

题目数据[1 4 2 3 5]，规定首个元素编号为1。
左侧首个大于：建立一个单调递减的栈（底大顶小），得到每个新元素后，先和栈顶元素比较，如果栈顶元素小，则出栈；直到栈顶元素大于新元素，或栈为空为止。
注意！！栈里存的是下标。

过程↓：

第一项是1，此时栈为空，直接输出0，把1的坐标压入栈。

第二项是4，此时栈顶是1，比较大小，1<4不满足递减，把1弹出，此时栈为空，直接输出0，把4的坐标压入栈。
第三项是2，此时栈顶是4，比较大小，4>2满足递减，此时栈顶为4，输出4的坐标2，把2的坐标压入栈。

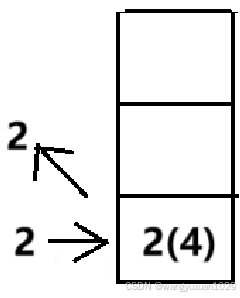
第四项是3，此时栈顶是2，比较大小，2<3不满足递减，弹出2，此时栈顶为4，输出4的坐标2，把3的坐标压入栈。

第五项是5，此时栈顶是3，比较大小，3<5不满足递减，弹出3，此时栈顶为4。

再次与栈顶比较，此时栈顶是4，比较大小，4<5不满足递减，弹出4，此时栈空，输出0，压入5的坐标。

模板：

//递减栈，从栈底向栈顶递减
stack<int> stck;
for(int i=1;i<=n;i++)
{
	//比目标元素i小的，从栈顶弹出，维护严格单调递增栈
	while(!stck.empty()&&arr[stck.top()]<=arr[i])
	{
		stck.pop();
	}
	//处理栈顶元素
	ans[i]=stck.empty()?0:stck.top();
	//目标元素下标入栈
	stck.push(i);
}