本部分的学习参考柯熙政老师的《无限光通信中的空间光——光纤耦合技术》及欧攀老师的《高等光学仿真(MATLAB版)》,为自学笔记,博客末尾附上了在学习过程中参考的博客内容。
单模光纤的归一化相位常数
归一化相位常数定义为:
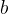

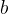
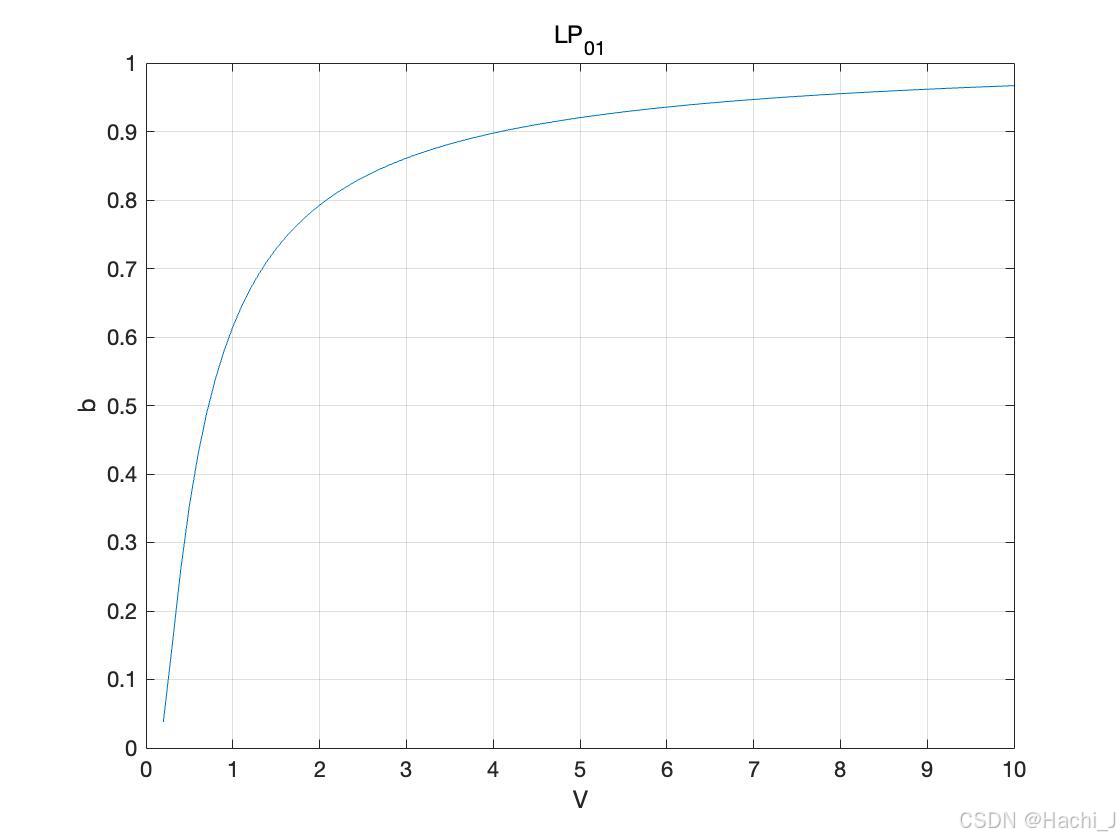
绘制LP01模的V和b的关系曲线如下:
Vmax = 10; % V的最大值为10
N =100; % 共计算(0.1,10)中的100个点
V = (1:N)/N*Vmax;
b = zeros (N, 1) ;
% 主循环,求解不同V对应的b值
for j = 1:N
Vtemp = V(j);
btemp = NaN;
i = 0;
while (isnan(btemp) && i<N+1)
init = (N-i) / N;
try
btemp = fzero (@ (b) ...
Vtemp+sqrt(1-b) * besselj(1, Vtemp*sqrt(1-b)) / ...
besselj(0, Vtemp*sqrt(1-b)) - Vtemp*sqrt (b) * ...
besselk(1, Vtemp*sqrt(b)) /besselk(0, Vtemp*sqrt(b)), init) ;
catch
end
i = i+1;
end
b(j) = btemp;
end
plot (V, b);单模光纤的光功率填充因子
光功率填充因子表示纤芯中光功率占光纤总功率的比重。在光纤激光器中,通过优化光功率填充因子可以提高激光器的增益效率和输出功率;在光纤通信中,光功率填充因子可以用于评估光纤的传输性能和稳定性。
对于一个特定的波导模式V(V是光纤归一化频率,是指光波导电磁模式的截止频率对光纤波导结构量的比值,这个比值依赖于纤芯的几何尺寸(如纤芯半径)和折射率剖面,故这里这样描述),其光纤纤芯中光功率填充因子的计算公式如下(方法一):
对于LP01模的单模光纤,将下标l换为1即可得到单模光纤的光功率填充因子的计算公式。
还可以根据单模光纤中归一化光强公式,通过积分来计算其纤芯中的光功率填充因子,光纤中归一化光强公式在之前的内容中已经给出,填充因子的计算公式如下(方法二):
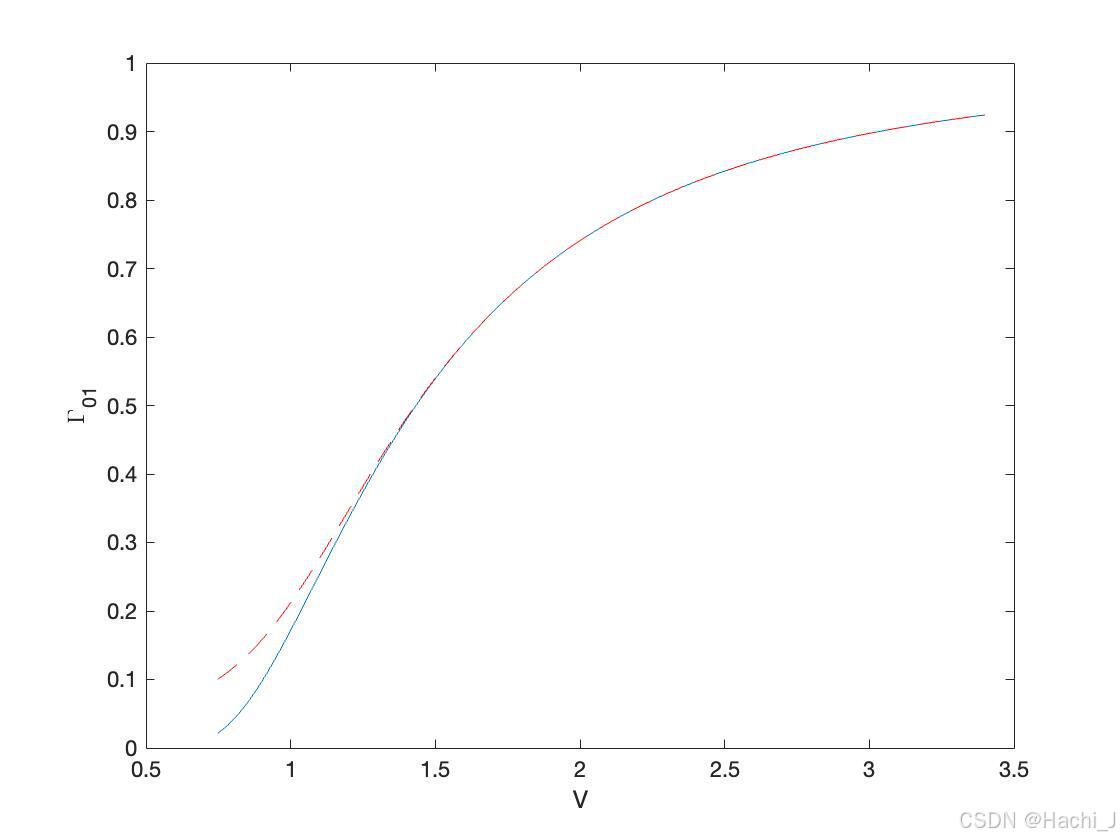
用以上两种方法得到的V与单模光纤的光功率填充因子的曲线如下(方法二为红色虚线):
从图中可以看出当V<1时,通过积分计算得到的计算结果与根据式计算得到的结果误差较大,而当V>1.5时两者得到的结果趋于一致。这是因为,当V值比较小时,光纤中的光功率大多分布在包层中。
% 根据定义计算LP01模的光功率填充因子
Gamma1 = (1-U.^2./V.^2).* (1-besselj(0,U).^2./(besselj(1, U).*besselj(-1, U)));
% 根据积分计算LP01模的光功率填充因子
for i = 1: length (V)
Pcore (i) = quad (@ (R) R.*besselj (0, U (i) *R) .^2, 0, 1) ;
Pclad (i) = quad (@ (R) R.*besselj (0, U (i))^2.*besselk (0,W(i) *R) .^2./besselk (0, W(i)) ^2, 1,5) ;
Gamma2 (i) = Pcore (i) / (Pcore (i) +Pclad (i) ) ;
end
figure
plot (V, Gamma1, V, Gamma2, ' r--')
xlabel ('V' )
ylabel ('\Gamma_{01}')单模光纤的模场直径(模场半径)
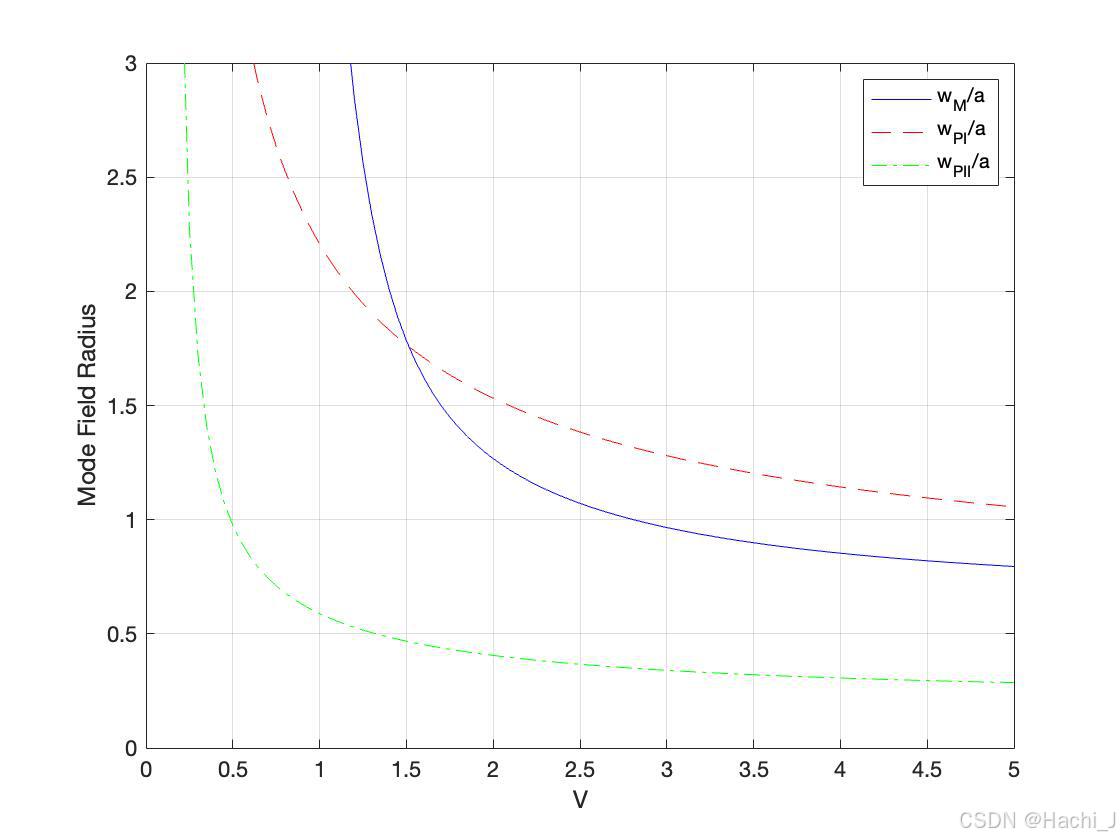
在考查单模光纤的性能参数时,一个十分重要的性能参数是光纤中传输模场的几何分布,即单模光纤的模场直径(mode feild diameter,MFD)或模场半径。模场半径可以由主模式LP01模的模场分布决定。多模光纤的模场半径与纤芯半径几乎相等,但是单模光纤的模场半径一般不等于纤芯半径,这是因单模光纤中并非所有的光都由纤芯承载并局限于纤芯内传播。
当光纤的归一化频率V >1.2时,可以用高斯函数来近似描述光纤内模式LP01模的模场分布。此时,可以将电场分布近似为
目前有好几种定义光纤模场直径大方法下面介绍目前常用的三种方法。
Marcuse模场半径
高斯光束耦合进光纤基模的功率比率取决于其束腰半径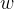

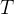
其中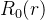

通过上式,求得半径相关的经验公式如下
其中,A、B和C与光纤的折射率剖面分布参数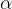
对于阶跃折射率光纤,Marcuse模场半径的经验公式为:
第一类Petermann模场半径
前面介绍的Marcuse模场半径是根据高斯光束的最大功率耦合效率来定义的,这种定义方式在物理意义上很直观。但是,是否能够根据光纤内的模场分布函数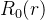
Petermann将其中的高斯函数替换为光纤的模场分布函数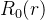
对于阶跃折射率光纤,光纤模场分布函数已在之前的内容中给出,将上式代入,可以得到阶跃折射率光纤的第一类Petermann模场半径的相关公式:
第二类Petermann模场半径
第一类中的模场半径定义只包含了光纤模场的近场特性,而在很多情况下希望利用光纤模场的远场特性,即产生了第二类Petermann模场半径:
同上,对于阶跃折射率光纤,第二类Petermann模场半径计算公式为:
matlab绘制三者曲线
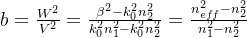
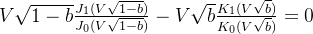
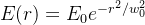
![T=[\frac{2\sqrt{2\pi }}{w}\int_{0}^{\infty }e^{-\frac{r^2}{w^2}}R_0(r)rdr]^2](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9U%3D%5B%5Cfrac%7B2%5Csqrt%7B2%5Cpi%20%7D%7D%7Bw%7D%5Cint_%7B0%7D%5E%7B%5Cinfty%20%7De%5E%7B-%5Cfrac%7Br%5E2%7D%7Bw%5E2%7D%7DR_0%28r%29rdr%5D%5E2)

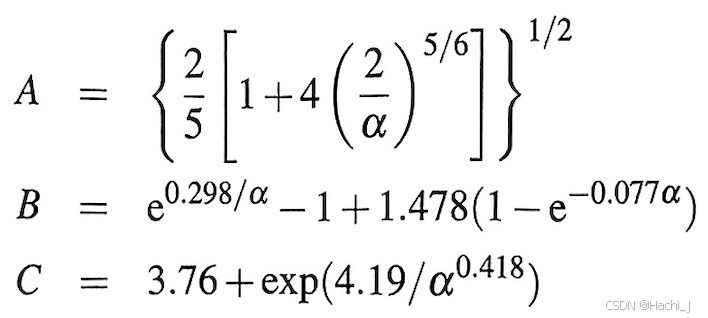
![w_{PI}^2=2\frac{\int_{0}^{\infty }[R_0(r)]^2r^3dr}{\int_{0}^{\infty }[R_0(r)]^2rdr}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT93_%7BPI%7D%5E2%3D2%5Cfrac%7B%5Cint_%7B0%7D%5E%7B%5Cinfty%20%7D%5BR_0%28r%29%5D%5E2r%5E3dr%7D%7B%5Cint_%7B0%7D%5E%7B%5Cinfty%20%7D%5BR_0%28r%29%5D%5E2rdr%7D)
![w_{PII}^2=2\frac{\int_{0}^{\infty }[R_0(r)]^2r^3dr}{\int_{0}^{\infty }[R_0(r)/dr]^2rdr}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT93_%7BPII%7D%5E2%3D2%5Cfrac%7B%5Cint_%7B0%7D%5E%7B%5Cinfty%20%7D%5BR_0%28r%29%5D%5E2r%5E3dr%7D%7B%5Cint_%7B0%7D%5E%7B%5Cinfty%20%7D%5BR_0%28r%29/dr%5D%5E2rdr%7D)